PSEB 10th Class Maths Solutions Chapter 13 ਸਤੁਦਾ ਖੇਤਰਫਲ ਅਤੇ ਆਇਤਨ Ex 13.5

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 13 ਸਤੁਦਾ ਖੇਤਰਫਲ ਅਤੇ ਆਇਤਨ Ex 13.5 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 10 Maths Chapter 13 ਸਤੁਦਾ ਖੇਤਰਫਲ ਅਤੇ ਆਇਤਨ Exercise 13.5

ਪ੍ਰਸ਼ਨ 1.
3 mm ਵਿਆਸ ਵਾਲੇ ਤਾਂਬੇ ਦੇ ਇੱਕ ਤਾਰ ਨੂੰ 12 cm ਲੰਬੇ ਅਤੇ 10 cm ਵਿਆਸ ਵਾਲੇ ਇੱਕ ਬੇਲਣ ‘ਤੇ ਇਸ ਪ੍ਰਕਾਰ ਲਪੇਟਿਆ ਜਾਂਦਾ ਹੈ ਕਿ ਉਹ ਬੇਲਣ ਦੇ ਵਕਰ ਤਲ ਨੂੰ ਪੂਰੀ ਤਰ੍ਹਾਂ ਢੱਕ ਲੈਂਦਾ ਹੈ । ਤਾਰ ਦੀ ਲੰਬਾਈ ਅਤੇ ਮਾਨ (ਭਾਰ) ਪਤਾ ਕਰੋ, ਇਹ ਮੰਨਦੇ ਹੋਏ ਕਿ ਤਾਂਬੇ ਦੀ ਘਣਤਾ 8.88 gਤਿ cm³ ਹੈ ।
ਹੱਲ:
ਤਾਰ ਦਾ ਵਿਆਸ (d) = 3 mm
∴ ਤਾਰ ਦਾ ਅਰਧ ਵਿਆਸ (r) = \(\frac{3}{2}\) mm = \(\frac{3}{20}\) cm

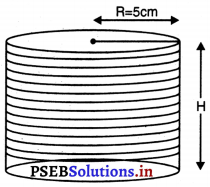
ਬੇਲਣ ਦਾ ਵਿਆਸ = 10 cm
ਬੇਲਣ ਦਾ ਅਰਧ ਵਿਆਸ (R) = 5 cm
ਬੇਲਣ ਦੀ ਉੱਚਾਈ (H) = 12 cm
ਬੇਲਣ ਦਾ ਪਰਿਮਾਪ = ਲਪੇਟੇ ਤਾਰ ਦੀ ਲੰਬਾਈ
2πR = ਇੱਕ ਲਪੇਟੇ ਤਾਰ ਦੀ ਲੰਬਾਈ
\(\frac{22}{7}\) × 2 × 5 = ਇੱਕ ਲਪੇਟੇ ਤਾਰ ਦੀ ਲੰਬਾਈ
\(\frac{220}{7}\) = ਲਪੇਟੇ ਤਾਰ ਦੀ ਲੰਬਾਈ

∴ ਪ੍ਰਯੋਗ ਕੀਤੀ ਤਾਰ ਦੀ ਲੰਬਾਈ = ਲਪੇਟਿਆਂ ਦੀ ਸੰਖਿਆ × ਇੱਕ ਲਪੇਟੇ ਵਿੱਚ ਪ੍ਰਯੋਗ ਕੀਤੀ ਤਾਰ ਦੀ ਲੰਬਾਈ
H = 40 × \(\frac{220}{7}\) cm
= 1257.14 cm
ਪ੍ਰਯੋਗ ਕੀਤੀ ਤਾਰ ਦਾ ਆਇਤਨ = πr²H
= \(\frac{22}{7}\) × \(\frac{3}{20}\) × \(\frac{3}{20}\) × 1257.14 cm³ = 88.89 cm³
1 cm³ ਤਾਰ ਦਾ ਮਾਨ = 8.88 gm
88.89 cm³ ਤਾਰ ਦਾ ਮਾਨ = 8.88 × 88.89
= 789.41 gm

ਪ੍ਰਸ਼ਨ 2.
ਇੱਕ ਸਮਕੋਣ ਤ੍ਰਿਭੁਜ, ਜਿਸ ਦੀਆਂ ਭੁਜਾਵਾਂ 3 cm ਅਤੇ 4 cm ਹਨ (ਕਰਣ ਤੋਂ ਇਲਾਵਾ), ਨੂੰ ਉਸਦੇ ਕਰਣ ਦੇ ਅਨੁਸਾਰ ਘੁਮਾਇਆ ਜਾਂਦਾ ਹੈ । ਇਸ ਤਰ੍ਹਾਂ ਪ੍ਰਾਪਤ ਦੋਹਰੇ ਥੰਕੂ (double cone) ਦੇ ਆਇਤਨ, ਅਤੇ ਸਤ੍ਹਾ ਦਾ ਖੇਤਰਫਲ ਪਤਾ ਕਰੋ । ( ਦਾ ਮੁੱਲ ਜੋ ਠੀਕ ਲੱਗੇ ਲੈ ਲਵੋ ॥
ਹੱਲ:
ਮੰਨ ਲਉ △ABC ਸਮਕੋਣ ਤ੍ਰਿਭੁਜ ਹੈ, ਜਿਸਦਾ A ਉੱਤੇ ਸਮਕੋਣ ਹੈ । AB ਅਤੇ AC ਦਾ ਮਾਪ ਕ੍ਰਮਵਾਰ 3 cm ਅਤੇ 4 cm ਹੈ । ਭੁਜਾ BC (ਕਰਣ ਦੀ ਲੰਬਾਈ
= \(\sqrt{3^{2}+4^{2}}\) = \(\sqrt {9+16}\) = 5 cm
ਇੱਥੇ AO (ਜਾਂ A’O) ਪ੍ਰਾਪਤ ਦੋਵੇਂ ਪਾਸੇ ਸਾਂਝੇ ਅਧਾਰ ਦੀ ਅਰਧ ਵਿਆਸ ਸਮਕੋਣ ਤਿਭੁਜ ਭੁਜਾ BC ਦੇ ਆਸ-ਪਾਸ ਘੁੰਮ ਕੇ ਬਣੀ ਹੈ ।

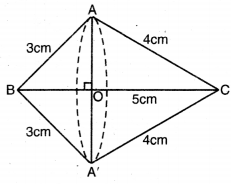
ਸ਼ੰਕੂ BAA’ ਦੀ ਉੱਚਾਈ BO ਅਤੇ ਤਿਰਛੀ ਉੱਚਾਈ 3 cm ਹੈ ।
ਸ਼ੰਕੂ CAA’ ਦੀ ਉੱਚਾਈ CO ਅਤੇ ਤਿਰਛੀ ਉੱਚਾਈ 4 cm ਹੈ ।
ਹੁਣ △AOB ~ △CAB (AA ਸਮਰੂਪਤਾ)
∴ \(\frac{AO}{4}\) = \(\frac{3}{5}\)
⇒ AO = \(\frac{4×3}{5}\) = \(\frac{12}{5}\) cm
ਨਾਲ ਹੀ ਉਹ \(\frac{BO}{3}\) = \(\frac{3}{5}\)
⇒ BO = \(\frac{3×3}{5}\) = \(\frac{9}{5}\) cm
∴ CO = BC – OB
= 5 – \(\frac{9}{5}\)
= \(\frac{16}{5}\) cm
∴ ਦੋਹਰੇ ਦੋਹਰੇ ਸ਼ੰਕੂ ਦਾ ਆਇਤਨ
= ਸ਼ੰਕੂ ABA’ ਦਾ ਆਇਤਨ + ਸ਼ੰਕੂ ACA’ ਦਾ ਆਇਤਨ
= \(\frac{1}{3}\)π OA².OB + \(\frac{1}{3}\)π OA².OC
= \(\frac{1}{3}\)π OA²(OB + OC)
= \(\frac{1}{3}\) × \(\frac{22}{7}\) × \(\frac{12}{5}\) × \(\frac{12}{5}\) (\(\frac{9}{5}\) + \(\frac{16}{5}\) )
= \(\frac{22 \times 4 \times 12}{7 \times 5 \times 5}\) × \(\frac{25}{5}\)
= \(\frac{1056}{35}\) = 30\(\frac{6}{35}\) cm³
∴ ਦੋਹਰੇ ਸ਼ੰਕੂ ਦਾ ਆਇਤਨ = 30\(\frac{6}{35}\) cm³.
ਦੋਹਰੇ ਸ਼ੰਕੂ ਦੀ ਸਤ੍ਹਾ ਦਾ ਖੇਤਰਫਲ
= ਸ਼ੰਕੂ ABA ਦੀ ਸੜਾਂ ਦਾ ਖੇਤਰਫਲ + ਸ਼ੰਕੂ ACA ਦੀ ਸਤ੍ਹਾ ਦਾ ਖੇਤਰਫਲ
= π. AO. AB + π. AO.A’C

ਪ੍ਰਸ਼ਨ 3.
ਇੱਕ ਟੈਂਕੀ, ਜਿਸਦੇ ਅੰਦਰੂਨੀ ਮਾਪ 150 cm × 120 cm × 110 cm ਹਨ, ਵਿੱਚ 129600 cm³ ਪਾਣੀ ਹੈ । ਦੇ ਇਸ ਪਾਣੀ ਵਿੱਚ ਕੁੱਝ ਛੇਕਾਂ ਵਾਲੀਆਂ ਇੱਟਾਂ ਉਦੋਂ ਤੱਕ ਪਾਈਆਂ ਜਾਂਦੀਆਂ ਹਨ ਜਦੋਂ ਤੱਕ ਕਿ ਟੈਂਕੀ ਪੂਰੀ ਉੱਪਰ ਤੱਕ ਭਰ ਨਾ ਜਾਵੇ । ਹਰੇਕ ਇੱਟ ਆਪਣੇ ਆਇਤਨ ਦਾ \(\frac{1}{17}\) ਪਾਣੀ ਸੋਖ ਲੈਂਦੀ ਹੈ । ਜੇਕਰ ਹਰੇਕ ਇੱਟ ਦਾ ਮਾਪ 22.5 cm × 7.5 cm × 6.5 cm ਹੋਵੇ, ਤਾਂ ਟੈਂਕੀ ਵਿਚ ਕੁੱਲ ਕਿੰਨੀਆਂ ਇੱਟਾਂ ਪਾਈਆਂ ਜਾ ਸਕਦੀਆਂ ਹਨ, ਤਾਂ ਕਿ ਉਸ ਤੋਂ ਪਾਣੀ ਬਾਹਰ ਨਾ ਆਵੇ ?
ਹੱਲ:
ਇੱਟਾਂ ਦਾ ਆਇਤਨ = 22.5 × 7.5 × 6.5 cm³
= 1096.87 cm3
ਟੈਂਕੀ ਦਾ ਆਇਤਨ = 150 × 120 × 110 cm³
= 1980000
ਮੰਨ ਲਉ ਇੱਟਾਂ ਦੀ ਸੰਖਿਆ = n
ਇੱਟਾਂ ਦਾ ਆਇਤਨ = n [1096.87] cm³
ਇੱਟਾਂ ਲਈ ਲੋੜੀਂਦੇ ਪਾਣੀ ਦਾ ਆਇਤਨ
= (1980000 – 129600) cm³
= 1850400 cm³
ਹਰੇਕ ਇੱਟ ਆਪਣੇ ਆਇਤਨ ਦਾ \(\frac{1}{17}\) ਵਾਂ ਪਾਣੀ ਸੋਖ ਲੈਂਦੀ ਹੈ |
ਇੱਟਾਂ ਦੁਆਰਾ ਸੋਖਿਆ ਪਾਣੀ ਦਾ ਆਇਤਨ = \(\frac{17}{10}\) × ਇੱਟਾਂ ਲਈ ਲੋੜੀਂਦੇ ਪਾਣੀ ਦਾ ਆਇਤਨ
= \(\frac{17}{10}\) × 1850400 cm³
ਇੱਟਾਂ ਦੁਆਰਾ ਸੋਖੇ ਪਾਣੀ ਦਾ ਆਇਤਨ
= 1966050 cm³
n ਇੱਟਾਂ ਦਾ ਕੁੱਲ ਆਇਤਨ
= ਇੱਟਾਂ ਦੁਆਰਾ ਸੋਖੇ ਪਾਣੀ ਦਾ ਆਇਤਨ
n[1096.87] cm³ = 1966050 cm³
n = \(\frac{1966050}{1096.42}\)
n = 1792.42
ਪ੍ਰਯੋਗ ਕੀਤੀਆਂ ਇੱਟਾਂ ਦੀ ਸੰਖਿਆ = 1792

ਪ੍ਰਸ਼ਨ 4.
ਕਿਸੇ ਮਹੀਨੇ ਦੇ 15 ਦਿਨਾਂ ਵਿੱਚ, ਇੱਕ ਨਦੀ ਦੀ ਘਾਟੀ ਵਿੱਚ 10 cm ਵਰਖਾ ਹੋਈ । ਜੇਕਰ ਇਸ ਘਾਟੀ ਦਾ ਖੇਤਰਫਲ 97280 km2 ਹੈ, ਤਾਂ ਦਰਸਾਉ ਕਿ ਕੁੱਲ ਵਰਖਾ ਲਗਭਗ ਤਿੰਨ ਨਦੀਆਂ ਦੇ ਆਮ ਪਾਣੀ ਦੇ ਜੋੜ ਦੇ ਬਰਾਬਰ ਸੀ, ਜਦੋਂ ਕਿ ਹਰੇਕ ਨਦੀ 1072 km ਲੰਬੀ, 75 m ਚੌੜੀ ਅਤੇ 3 m ਡੂੰਘੀ ਹੈ ।
ਹੱਲ:
ਘਾਟੀ ਦਾ ਖੇਤਰਫਲ = 97280 km²
ਘਾਟੀ ਵਿਚ ਬਾਰਿਸ਼ = 10 cm
∴ ਕੁੱਲ ਵਰਖਾ ਦਾ ਆਇਤਨ
= 97280 × \(\frac{10}{100}\) × \(\frac{1}{1000}\) km³
= 9728 km³

ਪ੍ਰਸ਼ਨ 5.
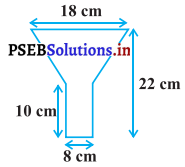
ਟੀਨ ਦੀ ਬਣੀ ਹੋਈ ਇੱਕ ਤੇਲ ਦੀ ਕੁੱਪੀ 10 cm ਲੰਬੇ ਇੱਕ ਬੇਲਣ ਵਿੱਚ ਇੱਕ ਸ਼ੰਕੂ ਦੇ ਸ਼ੌਕ ਨੂੰ ਜੋੜਨ ਨਾਲ ਬਣੀ ਹੈ । ਜੇਕਰ ਇਸ ਦੀ ਕੁੱਲ ਉੱਚਾਈ 22 cm ਹੈ ਅਤੇ ਬੇਲਨਾਕਾਰ ਭਾਗ ਦਾ ਵਿਆਸ 8 cm ਹੈ ਅਤੇ ਕੁੱਪੀ ਦੇ ਉੱਪਰੀ ਸਿਰੇ ਦਾ ਵਿਆਸ 18 cm ਹੈ, ਤਾਂ ਇਸਦੇ ਬਣਾਉਣ ਵਿੱਚ ਲੱਗੀ ਟੀਨ ਦੀ ਚਾਦਰ ਦਾ ਖੇਤਰਫਲ ਪਤਾ ਕਰੋ (ਦੇਖੋ ਚਿੱਤਰ)।

ਹੱਲ:
ਕੁੱਪੀ ਦੇ ਉੱਪਰੀ ਸਿਰੇ ਦਾ ਵਿਆਸ = 18 cm
∴ ਕੁੱਪੀ ਦੇ ਉੱਪਰੀ ਸਿਰੇ ਦਾ ਅਰਧ ਵਿਆਸ (R) = \(\frac{18}{2}\) = 9 cm
ਕੁੱਪੀ ਦੇ ਆਧਾਰ ਦਾ ਵਿਆਸ = 8 cm
ਕੁੱਪੀ ਦੇ ਆਧਾਰ ਦਾ ਅਰਧ ਵਿਆਸ (r) = 4 cm
ਬੇਲਣਾਕਾਰ ਭਾਗ ਦੀ ਉੱਚਾਈ (h) = 10 cm
ਸ਼ੌਨਕ ਦੀ ਉੱਚਾਈ (H) = (22 – 10)
= 12 cm
ਸ਼ੌਨਕ ਦੀ ਤਿਰਛੀ ਉੱਚਾਈ (l)
= \(\sqrt{\mathrm{H}^{2}+(\mathrm{R}-r)^{2}}\)
= \(\sqrt{(12)^{2}+(9-4)^{2}}\)
= \(\sqrt{144+(5)^{2}}\)
= \(\sqrt {144+25}\) = \(\sqrt {169}\)
ਸ਼ੌਨਕ ਦੀ ਤਿਰਛੀ ਉੱਚਾਈ (l) = 13 cm
ਟੀਨ ਦੀ ਚੱਦਰ ਦਾ ਖੇਤਰਫਲ = ਬੇਲਣਾਕਾਰ ਆਧਾਰ ਦੀ ਵਕਰ ਸਤ੍ਹਾ ਦਾ ਖੇਤਰਫਲ + ਸ਼ੌਨਕ ਦੀ ਵਕਰ ਸੜਾ ਦਾ ਖੇਤਰਫਲ
= 2πrh + πL[R + r]
= 2 × \(\frac{22}{7}\) × 4 × 10 + \(\frac{212}{7}\) × 13[19 + 4] cm²
= 251.42 + 531.14 = 782.56 cm²
∴ ਪ੍ਰਯੋਗ ਕੀਤੀ ਧਾਤੂ ਦੀ ਚੱਦਰ ਦਾ ਕੁੱਲ ਖੇਤਰਫਲ
= 782.56 cm²

ਪ੍ਰਸ਼ਨ 6.
ਸ਼ੰਕੂ ਦੇ ਇੱਕ ਛਿਣਕ ਦੇ ਲਈ, ਪਹਿਲਾਂ ਸਪੱਸ਼ਟ ਕੀਤੇ ਸੰਕੇਤਾਂ ਦਾ ਪ੍ਰਯੋਗ ਕਰਦੇ ਹੋਏ, ਵਕਰ ਤਲ ਦਾ ਖੇਤਰਫਲ ਅਤੇ ਕੁੱਲ ਸਤ੍ਹਾ ਦਾ ਖੇਤਰਫਲ ਦੇ ਉਨ੍ਹਾਂ ਸੂਤਰਾਂ ਨੂੰ ਸਿੱਧ ਕਰੋ ਜੋ ਭਾਗ 13.5 ਵਿੱਚ ਦਿੱਤੇ ਗਏ ਹਨ ।
ਹੱਲ:
ਇਕ ਲੰਬ ਚੱਕਰਾਕਾਰ ਸ਼ੰਕੂ ਦੇ ਸ਼ੌਨਕ ਦੋ ਅਸਮਾਨ ਚੱਕਰਾਕਾਰ ਆਧਾਰ ਅਤੇ ਵਕਰ ਸਤਾ ਹਨ । ਮੰਨ ਲਉ ਭਾਗ VCD ਨੂੰ ਹਟਾ ਕੇ ਪ੍ਰਾਪਤ ਸ਼ੌਨਕ ACDB ਹੈ । ਦੋਹਾਂ ਦੇ ਆਧਾਰਾਂ ਦੇ ਕੇਂਦਰਾਂ ਨੂੰ ਮਿਲਾਉਣ ਵਾਲਾ ਰੇਖਾਖੰਡ OP ਛੰਨਕ ਦੀ ਉੱਚਾਈ ਕਹਾਉਂਦਾ ਹੈ । ਸ਼ੌਕ ACDB ਦਾ ਹਰੇਕ ਰੇਖਾਖੰਡ AC ਅਤੇ BD ਤਿਰਛੀ ਉੱਚਾਈ ਹੈ ।

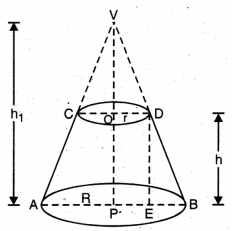
ਮੰਨ ਲਉ R ਅਤੇ r (R > r) ਸ਼ੰਕੂ (VAB) ਦੇ ਸ਼ੌਣਕ ACDB ਦੇ ਚੱਕਰਾਕਾਰ ਸਿਰਿਆਂ ਦਾ ਅਰਧ ਵਿਆਸ ਹਨ । ਅਸੀਂ ਸ਼ੰਕੂ ਆਕਾਰ ਭਾਗ VCD ਨੂੰ ਪੂਰਾ ਕਰਦੇ ਹਾਂ । ਮੰਨ ਲਉ ਕਿ ਮੈਂ ਅਤੇ 1 ਕੁਮਵਾਰ ਸਿੱਧੀ ਉੱਚਾਈ ਅਤੇ ਤਿਰਛੀ ਉੱਚਾਈ ਹੈ । ਤਾਂ OP = h ਅਤੇ AC = BD = l.
ਲੰਬ ਚੱਕਰਾਕਾਰ ਸ਼ੰਕੂ ਦੇ ਸ਼ੌਣਕ ਨੂੰ ਦੋ ਲੰਬ ਚੱਕਰਾਕਾਰ ਸ਼ੰਕੂਆਂ ਦੇ ਬਰਾਬਰ VAB ਅਤੇ VCD ਦੇ ਅੰਤਰ ਦੇ ਰੂਪ ਵਿਚ ਦੇਖਿਆ ਜਾ ਸਕਦਾ ਹੈ ।
ਮੰਨ ਲਉ ਸ਼ੰਕੂ VAB ਦੀ ਉੱਚਾਈ h, ਅਤੇ ਤਿਰਛੀ ਉਚਾਈ l ਹੈ । ਭਾਵ VP = h₁ ਅਤੇ VA = VB = l₁.
ਹੁਣ ਸਮਕੋਣ ਤ੍ਰਿਭੁਜ △DEB ਵਿਚ,
DB² = DE² + BE²
⇒ l² = h² + (R – r)²
⇒ l = \(\sqrt{h^{2}+(\mathrm{R}-r)^{2}}\)
ਦੁਬਾਗ △VOD ~ △VPB

= πl (R + r) ਵ. ਇਕਾਈਆਂ
∴ ਲੰਬ ਚੱਕਰਾਕਾਰ ਸ਼ੰਕੂ ਦੇ ਸ਼ੌਨਕ ਦੀ ਵਕਰ ਸਤਾ ਦਾ ਖੇਤਰਫਲ
= πl(R + r) ਵ. ਇਕਾਈਆਂ ਜਿੱਥੇ
l = \(\sqrt{h^{2}+(\mathrm{R}-r)^{2}}\)
ਲੰਬ ਚੱਕਰਾਕਾਰ ਸ਼ੰਕੂ ਦੇ ਸ਼ੌਨਕ ਦੀ ਕੁਲ ਸੜਾ ਦਾ ਖੇਤਰਫਲ
= ਵਕਰ ਸਤ੍ਹਾ ਦਾ ਖੇਤਰਫਲ+ਆਧਾਰ ਦਾ ਖੇਤਰਫਲ + ਉਪਰੀ ਸਿਰੇ ਦਾ ਖੇਤਰਫਲ
= πl(R + r) + πR² + πr²
= π[R² + r² + l(R + r)] ਵ. ਮੀ.

ਪ੍ਰਸ਼ਨ 7.
ਸ਼ੰਕੂ ਦੇ ਇੱਕ ਸ਼ੌਨਕ ਦੇ ਲਈ ਪਹਿਲਾਂ ਸਪੱਸ਼ਟ ਕੀਤੇ ਸੰਕੇਤਾਂ ਦਾ ਪ੍ਰਯੋਗ ਕਰਦੇ ਹੋਏ, ਆਇਤਨ ਦਾ ਉਹ ਸੂਤਰ | ਸਿੱਧ ਕਰੋ, ਜੋ ਭਾਗ 13.5 ਵਿਚ ਦਿੱਤਾ ਗਿਆ ਹੈ ।
ਹੱਲ:
ਇੱਕ ਲੰਬ ਚੱਕਰਾਕਾਰ ਸ਼ੰਕੂ ਦੇ ਸ਼ੌਨਕ ਦੇ ਅਸਮਾਨ ਚੱਕਰਾਕਾਰ ਆਧਾਰ ਅਤੇ ਵਕਰ ਸ਼ਤਾ ਹੁੰਦੀ ਹੈ । ਮੰਨ ਲਉ ਭਾਗ VCD ਨੂੰ ਹਟਾ ਕੇ ਪ੍ਰਾਪਤ ਸ਼ੌਨਕ ACDB ਹੈ ਦੋਹਾਂ ਦੇ ਆਧਾਰ ਨੂੰ ਮਿਲਾਉਣ ਵਾਲਾ ਰੇਖਾਖੰਡ OP ਸ਼ੌਨਕ ਦੀ ਲੰਬਾਈ ਕਹਾਉਂਦਾ ਹੈ ਸ਼ੌਨਕ ACDB ਦਾ ਹਰੇਕ ਰੇਖਾਖੰਡ AC ਅਤੇ BD ਤਿਰਛੀ ਉੱਚਾਈ ਕਹਾਉਂਦਾ ਹੈ ।

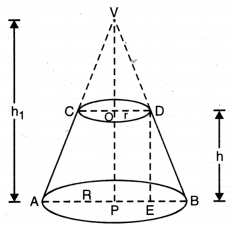
ਮੰਨ ਲਉ R ਅਤੇ r (R > r) ਸ਼ੰਕੂ (VAB) ਨੂੰ ਛਿੱਕ ACDB ਦੇ ਚੱਕਰਾਕਾਰ ਸਿਰਿਆਂ ਦੇ ਅਰਧ ਵਿਆਸ ਹਨ । ਅਸੀਂ ਸ਼ੰਕੂ ਵਾਲੇ ਭਾਗ VCD ਨੂੰ ਪੂਰਾ ਕਰਦੇ ਹਨ । ਮੰਨ ਲਉ ) ਅਤੇ ਕੁਮਵਾਰ ਸਿੱਧੀ ਅਤੇ ਤਿਰਛੀ ਉਚਾਈ ਹੈ । OP = h ਅਤੇ AC = BD = l.
ਲੰਬ ਚੱਕਰਾਕਾਰ ਸ਼ੰਕੂ ਦੇ ਸ਼ੌਨਕ ਦੇ ਦੋ ਲੰਬ ਚੱਕਰਕਾਰ ਸ਼ੰਕੂਆਂ ਦੇ ਬਰਾਬਰ VAB ਅਤੇ VCD ਦੇ ਅੰਤਰ ਰੂਪ ਵਿਚ ਦੇਖਿਆ ਜਾ ਸਕਦਾ ਹੈ ।
ਮੰਨ ਲਉ ਸ਼ੰਕੂ VAB ਦੀ ਉੱਚਾਈ h₁ ਅਤੇ ਤਿਰਛੀ ਉੱਚਾਈ l ਹੈ । ਭਾਵ VP = h₁ ਅਤੇ VA = VB = l₁.
∴ ਸ਼ੰਕੂ VCD ਦੀ ਉੱਚਾਈ = VP – OP
= h₁ – h
ਕਿਉਂਕਿ ਸਮਕੋਣ ਤ੍ਰਿਭੁਜ VOD ਅਤੇ VPB ਸਮਰੂਪ ਹਨ ।
⇒ \(\frac{VO}{VP}\) = \(\frac{OD}{PB}\) = \(\frac{h_{1}-h}{h_{1}}\) \(\frac{r}{R}\)
⇒ 1 – \(\frac{h}{h_{1}}\) = \(\frac{r}{R}\)

ਪਰ ਜੇਕਰ A₁ ਅਤੇ A₂ (A₁ > A₂) ਦੋ ਚੱਕਰਾਕਾਰ ਆਧਾਰਾਂ ਦੀ ਕੁੱਲ ਸਤਾ ਦਾ ਖੇਤਰਫਲ ਹੈ
A₁ = πR² ਅਤੇ A₂ = πr²
ਹੁਣ ਸ਼ੰਕੂ ਦੇ ਸ਼ੌਨਕ ਦਾ ਆਇਤਨ
= \(\frac{1}{3}\) πh(R² + r² + Rr)
= \(\frac{h}{3}\) (πR² + πr² + \(\sqrt{\pi \mathrm{R}^{2}} \sqrt{\pi r^{2}}\))
= \(\frac{h}{3}\) (A₁ + A₂ + \(\sqrt{A_{1} A_{2}}\))