PSEB 10th Class Maths Solutions Chapter 14 सांख्यिकी Ex 14.1

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 14 सांख्यिकी Ex 14.1 Textbook Exercise Questions and Answers

PSEB Solutions for Class 10 Maths Chapter 14 सांख्यिकी Ex 14.1

प्रश्न 1.
विद्यार्थियों के एक समूह द्वारा पर्यावरण संचेतना अभियान के अंतर्गत एक सर्वेक्षण किया गया, जिसमें उन्होंने एक मोहल्ले के 20 घरों में लगे हुए पौधों से संबंधित निम्नलिखित आँकड़े एकत्रित किए। प्रतिघर माध्य पौधों की संख्या ज्ञात कीजिए।

माध्य ज्ञात करने के लिए आपने किस विधि का प्रयोग किया और क्यों ?
हल :
क्योंकि पौधों की संख्या और घरों की संख्या मानों में कम है, इसलिए हमें प्रत्यक्ष विधि का प्रयोग करना चाहिए पौधों की संख्या

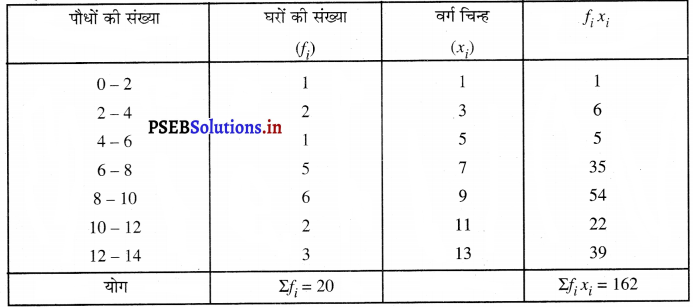
माध्य \(\overline{\mathrm{X}}=\frac{\Sigma f_{i} x_{i}}{\Sigma f_{i}}\)
= \(\frac{162}{20}\) = 8.1
अतः, प्रति घर पौधों को संख्या का माध्य 8.1 है।

प्रश्न 2.
किसी फैक्टरी के 50 श्रमिकों की दैनिक मजदूरी के निम्नलिखित बंटन पर विचार कीजिए :

एक उपर्युक्त विधि का प्रयोग करते हुए इस फैक्टरी के श्रमिकों की माध्य दैनिक मज़दूरी ज्ञात कीजिए।
हल :

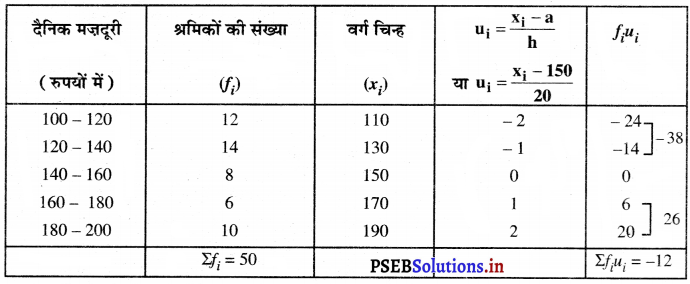
दिए गए आँकड़ों से
कल्पित मान (a) = 150
और वर्ग माप (h) = 20
∴ \(\bar{u}=\frac{\Sigma f_{i} u_{i}}{\Sigma f_{i}}\)
= \(\frac{-12}{50}\) = – 0.24
सूत्र का प्रयोग करने पर, माध्य (\(\overline{X}\)) = a + h\(\overline{u}\)
= 150 + (20) (- 0.24)
= 150 – 4.8 = 145.2
अतः फैक्टरी के श्रमिकों की माध्य दैनिक मज़दूरी ₹ 145.20 है।

प्रश्न 3.
निम्नलिखित बंटन एक मोहल्ले के बच्चों के दैनिक जेब खर्च दर्शाता है। माध्य जेब खर्च ₹18 है। लुप्त बारंबारता f ज्ञात कीजिए।

हल :

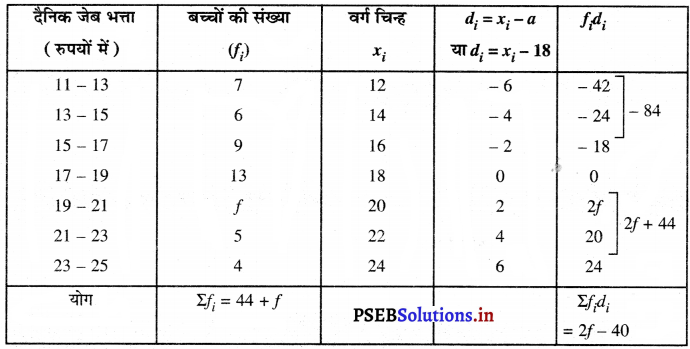
उपरोक्त आँकड़ों से
कल्पित माध्य (a) = 18
सूत्र का प्रयोग करने पर, माध्य \((\overline{\mathrm{X}})=a+\frac{\Sigma f_{i} d_{i}}{\Sigma f_{i}}\)

\(\overline{\mathrm{X}}=18+\frac{2 f-40}{44+f}\)

आँकड़ों का माध्य \((\overline{\mathrm{X}})\) = 18 …..(दिया है)
18 = 18 + \(\frac{2 f-40}{44+f}\)
\(\frac{2 f-40}{44+f}\) = 18 – 18 = 0 44 +f
2f – 40 = 0
2f = 40
f = \(\frac{40}{2}\) = 20
अतः, लुप्त बारंबारता f = 20 है।

प्रश्न 4.
किसी अस्पताल में, एक डॉक्टर द्वारा 30 महिलाओं की जाँच की गई और उनके हृदय स्पंदन (beat) की प्रति मिनट संख्या नोट करके नीचे दर्शाए अनुसार संक्षिप्त रूप में लिखी गई। एक उपयुक्त विधि चुनते हुए, इन महिलाओं के हृदय स्पंदन की प्रतिमिनट मध्य संख्या ज्ञात कीजिए।

हल :

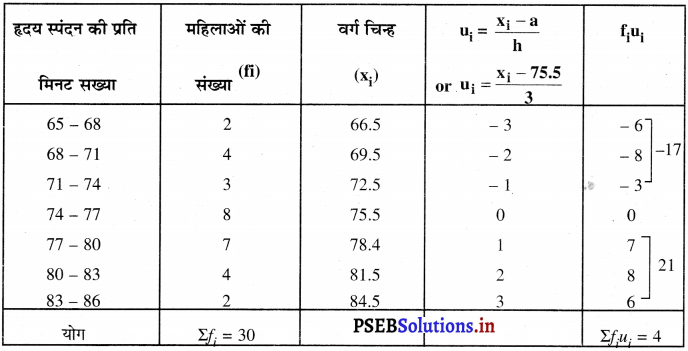
उपरोक्त आँकड़ो से,
कल्पित माध्य (a) = 75.5
वर्ग माप (h) = 3
\(\bar{u}=\frac{\Sigma f_{i} u_{i}}{\Sigma f_{i}}\)
= \(\frac{4}{30}\) = 0.13 (लगभग)
सूत्र का प्रयोग करने पर,
माध्य \((\overline{\mathrm{X}})=a+h \bar{u}\)
= 75.5 + 3 (0.13)
= 75.5 + 0.39
\(\overline{\mathrm{X}}\) = 78.89
अतः महिलाओं के हृदय स्पंदन की प्रति मिनट माध्य संख्या 78.89 है।

प्रश्न 5.
किसी फुटकर बाजार में, फल विक्रेता पेटियों में रखे आम बेच रहे थे। इन पेटियों में आमों की संख्याएँ भिन्न-भिन्न थीं। पेटियों की संख्या के अनुसार, आमों का बंटन निम्नलिखित था :

एक पेटी में रेखे आमों की माध्य संख्या ज्ञात कीजिए। आपने माध्य ज्ञात करने की किस विधि का प्रयोग किया ?
हल :
क्योंकि आमों की संख्या और पेटियों की संख्या के मान संख्यात्मक रूप से बड़े हैं इसलिए हम पद विचलन विधि का प्रयोग करेंगे।

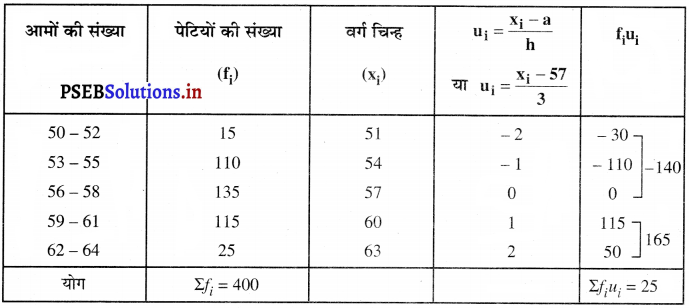
उपरोक्त आँकड़ो से,
कल्पित माध्य (a) = 57
वर्गमाप (h) = 3
∴ \(\bar{u}=\frac{\sum f_{i} u_{i}}{\sum f_{i}}\)
\(\bar{u}=\frac{25}{400}\) = 0.0625
सूत्र का प्रयोग करने पर, माध्य \((\overline{\mathrm{X}})=a+h \bar{u}\)
\(\overline{\mathrm{X}}\) = 57 + 3 (0.0625)
= 57 + 0.1875
= 57.1875
= 57.19 (लगभग)
अतः, पेटी में रखे आमों की माध्य संख्या 57.19 है।

प्रश्न 6.
निम्नलिखित सारणी किसी मोहल्ले के 25 परिवारों में भोजन पर हुए दैनिक व्यय को दर्शाती है :

एक उपयुक्त विधि द्वारा भोजन पर हुआ माध्य व्यय ज्ञात कीजिए।
हल:

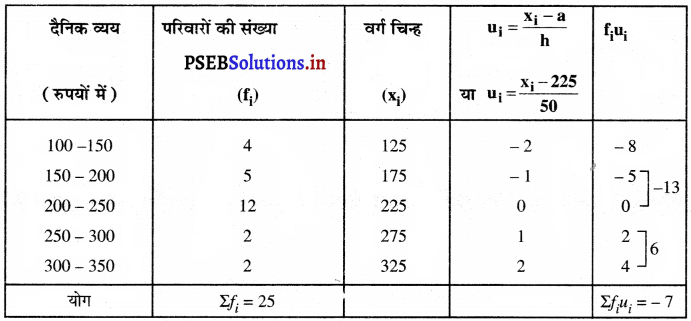
उपरोक्त आँकड़ों से,
कल्पित माध्य (a) = 225
वर्ग माप (h) = 50
∴ \(\bar{u}=\frac{\Sigma f_{i} u_{i}}{\Sigma f_{i}}\)

\(\bar{u}=-\frac{7}{25}\)
= – 0.28
सूत्र का प्रयोग करने पर, माध्य \((\overline{\mathrm{X}})=a+h \bar{u}\)
\(\overline{\mathrm{X}})\) = 225 + 50 (- 0.28)
\(\overline{\mathrm{X}})\) = 225 – 14
\(\overline{\mathrm{X}})\) = 211
अतः, भोजन पर हुआ माध्य व्यय ₹ 211 है।

प्रश्न 7.
वायु में सल्फर डाइआक्साइड (SO₂) की सांद्रता (भाग प्रतिमिलियन में) को ज्ञात करने के लिए, एक नगर के 30 को मोहल्लों से आँकड़ें एकत्रित किए गए, जिन्हें नीचे प्रस्तुत किया गया है :

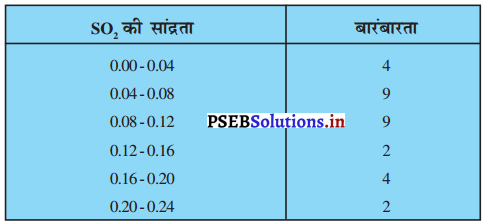
वायु में SO₂ की सांद्रता का माध्य ज्ञात कीजिए।
हल:

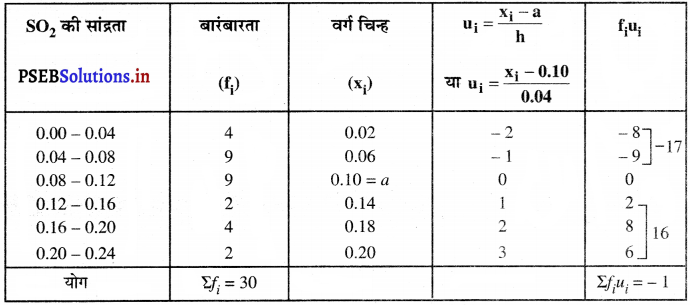
उपरोक्त आँकड़ों से
कल्पित माध्य (a) = 0.10
वर्ग माप (h) = 0.04
\(\bar{u}=\frac{\Sigma f_{i} u_{i}}{\Sigma f_{i}}=\frac{-1}{30}\)
= – 0.33 (लगभग)
सूत्र का प्रयोग करने पर, माध्य \((\overline{\mathrm{X}})=a+h \bar{u}\)
\(\overline{\mathrm{X}}\) = 0.10 + 0.04 (- 0.33)
= 0.10 – 0.0013 = 0.0987 (लगभग)
वायु में SO₂ की सांद्रता का माध्य 0.0987 ppm है।

प्रश्न 8.
किसी कक्षा अध्यापिका ने पूरे सत्र के लिए अपनी कक्षा के 40 विद्यार्थियों की अनुपस्थिति निम्नलिखित रूप में रिकार्ड (record) की। एक विद्यार्थी जितने दिन अनुपस्थित रहा उनका माध्य ज्ञात कीजिए :

हल:

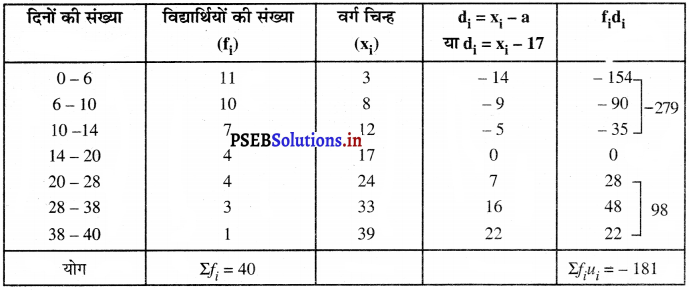
उपरोक्त आँकड़ों से,
कल्पित माध्य (a) = 17
सूत्र का प्रयोग करने पर,
माध्य \((\overline{\mathrm{X}})=a+\frac{\sum f_{i} d_{i}}{\sum f_{i}}\)

\(\overline{\mathrm{X}}\) = 17 + \(\frac{(-181)}{40}\)
= 17 – 4.52
= 12.48
अतः, एक विद्यार्थी जितने दिन अनुपस्थित रहा उनका माध्य 12.48 है।

प्रश्न 9.
निम्नलिखित सारणी 35 नगरों की साक्षरता दर ( प्रतिशत में ) दर्शाती है। माध्य साक्षरता दर ज्ञात कीजिए :

हल :

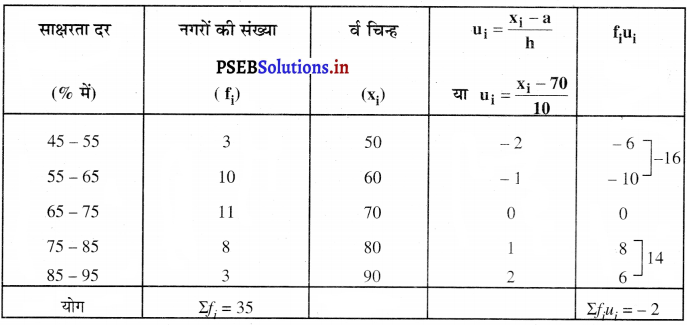
उपरोक्त आँकड़ों से,
कल्पित माध्य (a) = 70
वर्ग माप (h) = 10
∴ u = \(\bar{u}=\frac{\sum f_{i} u_{i}}{\Sigma f_{i}}=\frac{-2}{35}\) = – 0.07

सूत्र का प्रयोग करने पर,
माद्य \((\overline{\mathrm{X}})=a+h \bar{u}\)
\((\overline{\mathrm{X}}\) = 70 + 10 (-0.057)
= 70 – 0.57 = 69.43
अतः, माध्य साक्षरता दर 69.43% है।