Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 14 ਅੰਕੜਾਵਿਗਿਆਨ Ex 14.1 Textbook Exercise Questions and Answers.
PSEB Solutions for Class 10 Maths Chapter 14 ਅੰਕੜਾਵਿਗਿਆਨ Exercise 14.1
ਪ੍ਰਸ਼ਨ 1.
ਵਿਦਿਆਰਥੀਆਂ ਦੇ ਇੱਕ ਸਮੂਹ ਦੁਆਰਾ ਆਪਣੇ ਵਾਤਾਵਰਨ ਚੇਤਨਾ ਅਭਿਆਨ ਦੇ ਅਧੀਨ ਇੱਕ ਸਰਵੇਖਣ ਕੀਤਾ ਗਿਆ ਜਿਸ ਵਿੱਚ ਉਹਨਾਂ ਨੇ ਇੱਕ ਮੁਹੱਲੇ ਦੇ 20 ਘਰਾਂ ਵਿੱਚ ਲੱਗੇ ਪੌਦਿਆਂ ਨਾਲ ਸੰਬੰਧਿਤ ਹੇਠਾਂ ਲਿਖੇ ਅੰਕੜੇ ਇਕੱਠੇ ਕੀਤੇ । ਪ੍ਰਤਿ ਘਰ ਦੀ ਮੱਧਮਾਨ (ਔਸਤ) ਪੌਦਿਆਂ ਦੀ ਸੰਖਿਆ ਪਤਾ ਕਰੋ ।

ਮੱਧਮਾਨ ਦਾ ਪਤਾ ਕਰਨ ਲਈ ਤੁਸੀਂ ਕਿਹੜੀ ਵਿੱਧੀ ਦਾ ਪ੍ਰਯੋਗ ਕੀਤਾ ਅਤੇ ਕਿਉਂ ?
ਹੱਲ:
ਕਿਉਂਕਿ ਪੌਦਿਆਂ ਦੀ ਸੰਖਿਆ ਅਤੇ ਘਰਾਂ ਦੀ ਸੰਖਿਆ ਦੇ ਮੁੱਲ ਘੱਟ ਹਨ ਇਸ ਲਈ ਅਸੀਂ ਪ੍ਰਤੱਖ ਵਿਧੀ ਦਾ ਪ੍ਰਯੋਗ ਕਰਾਂਗੇ
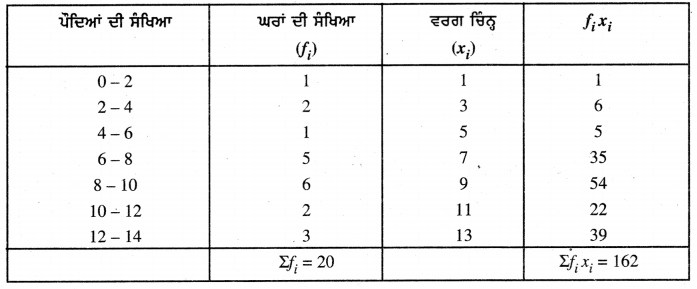
ਉਪਰੋਕਤ ਅੰਕੜਿਆਂ ਤੋਂ
ਮੱਧਮਾਨ \(\bar{X}\) = \(\frac{\Sigma f_{i} x_{i}}{\Sigma f_{i}}\)
= \(\frac{162}{20}\) = 8.1
ਇਸ ਲਈ ਪ੍ਰਤੀ ਘਰ ਪੌਦਿਆਂ ਦੀ ਮੱਧਮਾਨ ਸੰਖਿਆ 8.1 ਹੈ ।
ਪ੍ਰਸ਼ਨ 2.
ਕਿਸੇ ਫੈਕਟਰੀ ਦੇ 50 ਮਜਦੂਰਾਂ ਦੀ ਰੋਜ਼ਾਨਾ ਮਜ਼ਦੂਰੀ ਦੇ ਹੇਠਾਂ ਲਿਖੀ ਵੰਡ ਸਾਰਣੀ ਉੱਤੇ ਵਿਚਾਰ ਕਰੋ ।

ਇੱਕ ਸਹੀ (ਉਚਿਤ) ਵਿਧੀ ਦਾ ਪ੍ਰਯੋਗ ਕਰਦੇ ਹੋਏ, ਇਸ ਫੈਕਟਰੀ ਦੇ ਮਜ਼ਦੂਰਾਂ ਦੀ ਮੱਧਮਾਨ ਰੋਜ਼ਾਨਾ ਮਜ਼ਦੂਰੀ ਪੱਤਾ ਕਰੋ ।
ਹੱਲ:
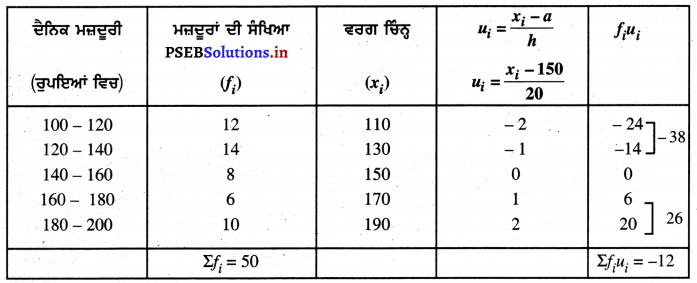
ਦਿੱਤੇ ਗਏ ਅੰਕੜਿਆਂ ਤੋਂ
ਕਾਲਪਨਿਕ ਮੱਧਮਾਨ (a) = 150
ਵਰਗ ਮਾਪ (h) = 20
∴ \(\bar{u}\) = \(\frac{\Sigma f_{i} u_{i}}{\Sigma f_{i}}\)
= \(\frac{-12}{50}\) = -0.24
ਸੂਤਰ ਦਾ ਪ੍ਰਯੋਗ ਕਰਨ ‘ਤੇ (\(\bar{X}\)) = a + h\(\bar{u}\)
= 150 + (20)(-0.24)
= 150 – 4.8 =145.2
∴ ਫੈਕਟਰੀ ਦੇ ਮਜ਼ਦੂਰਾਂ ਦੀ ਮੱਧਮਾਨ ਰੋਜ਼ਾਨਾ ਮਜ਼ਦੂਰੀ ₹ 145.20 ਹੈ ।
![]()
ਪ੍ਰਸ਼ਨ 3.
ਹੇਠ ਦਿੱਤੀ ਵੰਡ ਸਾਰਣੀ ਇੱਕ ਮੁਹੱਲੇ ਦੇ ਬੱਚਿਆਂ ਦਾ ਰੋਜ਼ਾਨਾ ਜੇਬ ਖ਼ਰਚ ਨੂੰ ਦਰਸਾਉਂਦੀ ਹੈ । ਮੱਧਮਾਨ ਜੇਬ ਖ਼ਰਚਾ ₹ 18 ਹੈ | ਅਗਿਆਤ ਬਾਰੰਬਾਰਤਾ ‘f ‘ ਪਤਾ ਕਰੋ :

ਹੱਲ:
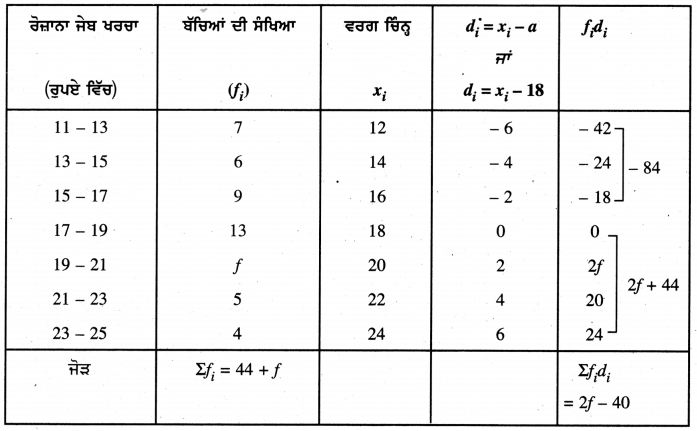
ਉਪਰੋਕਤ ਅੰਕੜਿਆਂ ਤੋਂ
ਕਾਲਪਨਿਕ ਮੱਧਮਾਨ (a) = 18
ਸੂਤਰ ਦਾ ਪ੍ਰਯੋਗ ਕਰਨ ‘ਤੇ, ਮੱਧਮਾਨ (\(\bar{X}\)) = a + \(\frac{\Sigma f_{i} d_{i}}{\Sigma f_{i}}\)
\(\bar{X}\) = 18 + \(\frac{2 f-40}{44+f}\)
ਪਰ, ਅੰਕੜਿਆਂ ਦਾ ਮੱਧਮਾਨ (\(\bar{x}\)) = 18 …….. (ਦਿੱਤਾ ਹੈ।)
∴ 18 = 18 + \(\frac{2 f-40}{44+f}\)
ਜਾਂ \(\frac{2 f-40}{44+f}\) = 18 – 18 = 0
ਜਾਂ 2f – 40 = 0
ਜਾਂ 2f = 40
ਜਾਂ f = \(\frac{40}{2}\) = 20
∴ ਅਗਿਆਤ ਬਾਰੰਬਾਰਤਾf = 20 ਹੈ । ਉੱਤਰ
ਪ੍ਰਸ਼ਨ 4.
ਕਿਸੇ ਹਸਪਤਾਲ ਵਿੱਚ, ਇੱਕ ਡਾਕਟਰ ਦੁਆਰਾ 30 ਇਸਤਰੀਆਂ ਦੀ ਜਾਂਚ ਕੀਤੀ ਗਈ ਅਤੇ ਉਨ੍ਹਾਂ ਦੀ ਦਿਲ ਦੀ ਧੜਕਣ (heart beat) ਪ੍ਰਤੀ ਮਿੰਟ ਨੋਟ ਕਰਕੇ ਹੇਠਾਂ ਦਰਸਾਉਂਦੀ ਵੰਡ ਸਾਰਣੀ ਵਿੱਚ ਸੰਖੇਪ ਰੂਪ ਨਾਲ ਲਿਖੀ ਗਈ । ਇੱਕ ਸਹੀ (ਉਚਿਤ) ਵਿਧੀ ਦੀ ਵਰਤੋਂ ਕਰਕੇ ਇਹਨਾਂ ਇਸਤਰੀਆਂ ਦੇ ਦਿਲ ਦੀ ਧੜਕਣ ਦੀ ਪ੍ਰਤੀ ਮਿੰਟ ਮੱਧਮਾਨ ਸੰਖਿਆ ਪਤਾ ਕਰੋ :

ਹੱਲ:
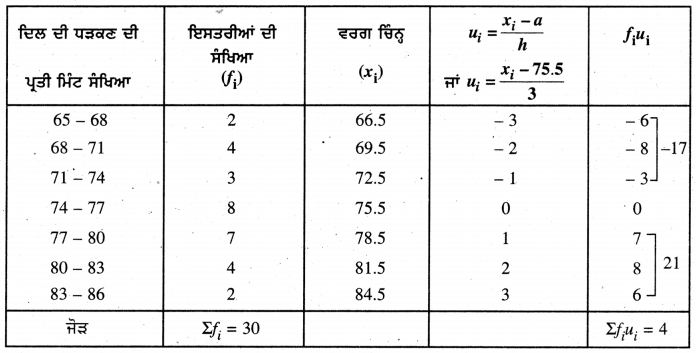
ਉਪ੍ਰੋਕਤ ਅੰਕੜਿਆਂ ਤੋਂ
ਕਾਲਪਨਿਕ ਮੱਧਮਾਨ (a) = 75.5
ਵਰਗ ਮਾਪ (h) = 3
∴ \(\bar{u}\) = \(\frac{\Sigma f_{i} u_{i}}{\Sigma f_{i}}\)
= \(\frac{4}{30}\) = 0.13 (ਲਗਭਗ)
ਸੂਤਰ ਦਾ ਪ੍ਰਯੋਗ ਕਰਨ ‘ਤੇ ਮੱਧਮਾਨ (\(\bar{X}\)) = a + h\(\bar{u}\)
= 75.5 + 3 (0.13)
= 75.5 + 0.39
\(\bar{X}\) = 7889
∴ ਇਸਤਰੀਆਂ ਦੇ ਦਿਲ ਦੀ ਧੜਕਣ ਦੀ ਪ੍ਰਤੀ ਮਿੰਟ ਮੱਧਮਾਨ ਸੰਖਿਆ 78.89 ਹੈ ।
![]()
ਪ੍ਰਸ਼ਨ 5.
ਕਿਸੇ ਬਜ਼ਾਰ ਵਿੱਚ, ਫਲ ਵਿਕੇਤਾ, ਪੇਟੀਆਂ ਵਿੱਚ ਰੱਖੇ ਅੰਬ ਵੇਚ ਰਹੇ ਸਨ । ਇਨ੍ਹਾਂ ਪੇਟੀਆਂ ਵਿੱਚ ਅੰਬਾਂ ਦੀ ਸੰਖਿਆ ਅਲੱਗ-ਅਲੱਗ ਸੀ । ਪੇਟੀਆਂ ਦੀ ਸੰਖਿਆ ਅਨੁਸਾਰ, ਅੰਬਾਂ ਦੀ ਵੰਡ ਹੇਠ ਲਿਖੇ ਅਨੁਸਾਰ ਸੀ :

ਇੱਕ ਪੇਟੀ ਵਿੱਚ ਰੱਖੀ ਅੰਬਾਂ ਦੀ ਮੱਧਮਾਨ ਸੰਖਿਆ ਪਤਾ ਕਰੋ । ਤੁਸੀਂ ਮੱਧਮਾਨ ਕੱਢਣ ਲਈ ਕਿਹੜੀ ਵਿੱਧੀ ਦਾ ਪ੍ਰਯੋਗ ਕੀਤਾ ਹੈ ?
ਹੱਲ:
ਕਿਉਂਕਿ ਅੰਬਾਂ ਦੀ ਸੰਖਿਆ ਅਤੇ ਪੇਟਿਆਂ ਦੀ ਸੰਖਿਆ ਦਾ ਮੁੱਲ ਜ਼ਿਆਦਾ ਹੈ । ਇਸ ਲਈ ਅਸੀਂ ਪਗ ਵਿਚਲਣ ਵਿਧੀ ਦਾ ਪ੍ਰਯੋਗ ਕਰਾਂਗੇ।
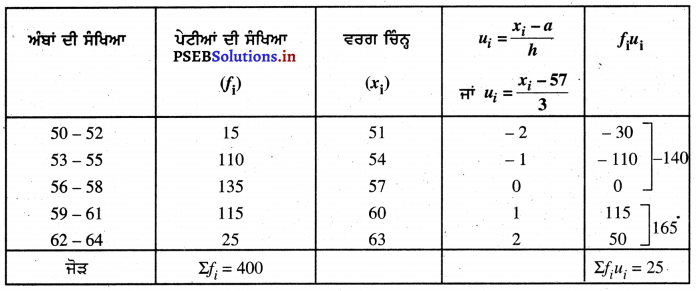
ਉਪਰੋਕਤ ਅੰਕੜਿਆਂ ਤੋਂ
ਕਾਲਪਨਿਕ ਮੱਧਮਾਨ (a) = 57
ਵਰਗ ਮਾਪ (h) = 3
∴ \(\bar{u}\) = \(\frac{\Sigma f_{i} u_{i}}{\Sigma f_{i}}\)
\(\bar{u}\) = \(\frac{25}{400}\) = 0.0625
ਸੂਤਰ ਦਾ ਪ੍ਰਯੋਗ ਕਰਨ ‘ਤੇ, (\(\bar{X}\)) = a + h\(\bar{u}\)
\(\bar{X}\) = 57 + 3 (0.0625)
= 57 + 0.1875
= 57.1875
= 57.19 ਲਗਭਗ
ਪੇਟੀ ਵਿੱਚ ਰੱਖੇ ਗਏ ਅੰਬਾਂ ਦੀ ਮੱਧਮਾਨ ਸੰਖਿਆ 57.19 ਹੈ ।
ਪ੍ਰਸ਼ਨ 6.
ਹੇਠਾਂ ਦਿੱਤੀ ਸਾਰਣੀ ਕਿਸੇ ਮੁਹੱਲੇ ਦੇ 25 ਪਰਿਵਾਰਾਂ ਦੇ ਭੋਜਨ ਉੱਪਰ ਹੋਏ ਰੋਜ਼ਾਨਾ ਖ਼ਰਚ ਨੂੰ ਦਰਸਾਉਂਦੀ ਹੈ :

ਇੱਕ ਉਚਿਤ ਵਿਧੀ ਦਾ ਪ੍ਰਯੋਗ ਕਰਕੇ ਭੋਜਨ ਉੱਪਰ ਹੋਏ ਖ਼ਰਚ ਦਾ ਮੱਧਮਾਨ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
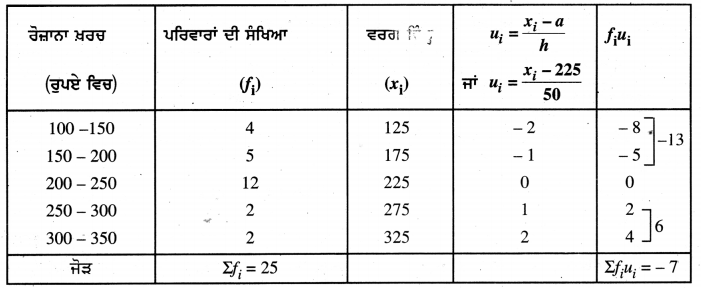
ਉਪਰੋਕਤ ਅੰਕੜਿਆਂ ਤੋਂ ।
ਕਾਲਪਨਿਕ ਮੱਧਮਾਨ (a) = 225
ਵਰਗ ਮਾਪ (h) = 50
∴ \(\bar{u}\) = \(\frac{\Sigma f_{i} u_{i}}{\Sigma f_{i}}\)
\(\bar{u}\) = \(-\frac{7}{25}\) = -0.28
ਸੂਤਰ ਦਾ ਪ੍ਰਯੋਗ ਕਰਨ ‘ਤੇ, ਮੱਧਮਾਨ (\(\bar{X}\)) = a + h\(\bar{u}\)
\(\bar{X}\) = 225 + 50 (0.28)
\(\bar{X}\) = 225 – 14
\(\bar{X}\) = 211
ਭੋਜਨ ਉੱਪਰ ਹੋਏ ਖ਼ਰਚ ਦਾ ਮੱਧਮਾਨ ₹211 ਹੈ ।
![]()
ਪ੍ਰਸ਼ਨ 7.
ਹਵਾ ਵਿੱਚ ਸਲਫਰ ਡਾਈਆਕਸਾਈਡ (SO2) ਦੀ ਮਾਤਰਾ (Concentration) ਭਾਗ ਪ੍ਰਤੀ ਮਿਲਿਅਨ ਵਿੱਚ ਪਤਾ ਕਰਨ ਲਈ ਇੱਕ ਇਲਾਕੇ ਦੇ 30 ਮੁਹੱਲਿਆਂ ਵਿੱਚੋਂ ਅੰਕੜੇ ਇਕੱਠੇ ਕੀਤੇ ਗਏ । ਜਿਹਨਾਂ ਨੂੰ ਹੇਠ ਦਿੱਤੇ ਅਨੁਸਾਰ ਵਰਗੀਕ੍ਰਿਤ ਕੀਤਾ ਗਿਆ :
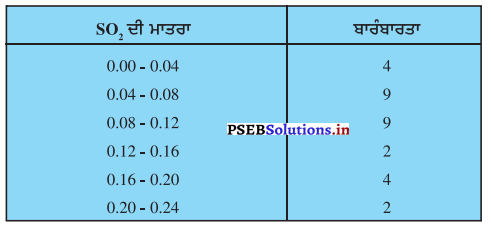
ਹਵਾ ਵਿੱਚ SO2 ਦੀ ਮਾਤਰਾ ਦਾ ਮੱਧਮਾਨ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
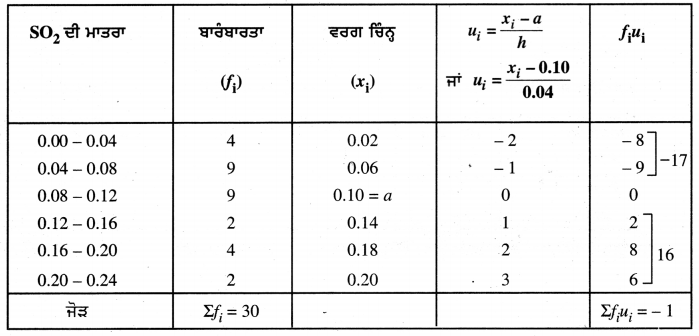
ਉਪਰੋਕਤ ਅੰਕੜਿਆਂ ਤੋਂ,
ਕਾਲਪਨਿਕ ਮੱਧਮਾਨ (a) = 0.10
ਵਰਗ ਮਾਪ (h) = 0.04
\(\bar{u}\) = \(\frac{\Sigma f_{i} u_{i}}{\Sigma f_{i}}\) = \(\frac{-1}{30}\) = -0.33 (ਲਗਭਗ)
ਸੂਤਰ ਦਾ ਪ੍ਰਯੋਗ ਕਰਨ ‘ਤੇ, (\(\bar{X}\)) = a + h\(\bar{u}\)
\(\bar{X}\) = 0.10 + 0.04(-0.33)
= 0.10 – 0.0013 = 0.0987 (ਲਗਭਗ)
ਹਵਾ ਵਿੱਚ SO2 ਦੀ ਮਾਤਰਾ ਦਾ ਮੱਧਮਾਨ 0.0987 ppm ਹੈ ।
ਪ੍ਰਸ਼ਨ 8.
ਕਿਸੇ ਜਮਾਤ ਦੀ ਅਧਿਆਪਕਾ ਨੇ ਪੂਰੇ ਸਾਲ ਦੌਰਾਨ ਆਪਣੀ ਜਮਾਤ ਦੇ 40 ਵਿਦਿਆਰਥੀਆਂ ਦੀ ਗੈਰਹਾਜ਼ਰੀ ਨੂੰ ਹੇਠ ਲਿਖੇ, ਅਨੁਸਾਰ ਰਿਕਾਰਡ ਕੀਤਾ ਗਿਆ । ਇੱਕ ਵਿਦਿਆਰਥੀ ਜਿੰਨੇ ਦਿਨ ਗੈਰਹਾਜ਼ਿਰ ਰਿਹਾ ਉਸ ਦਾ ਮੱਧਮਾਨ ਪਤਾ ਕਰੋ :
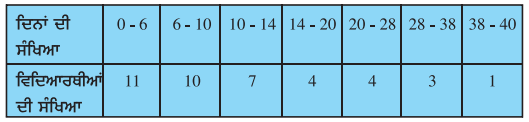
ਹੱਲ:
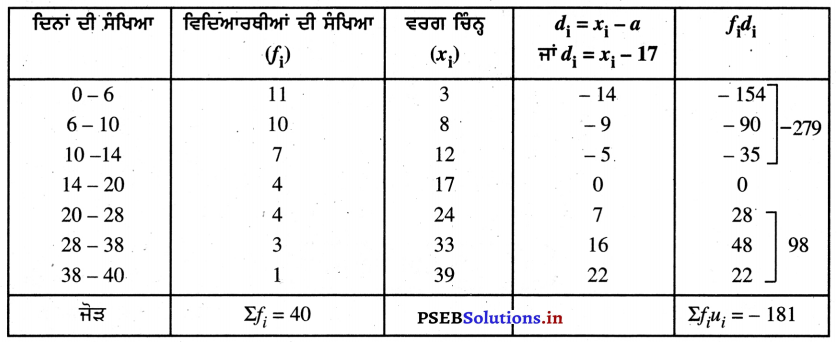
ਉਪਰੋਕਤ ਅੰਕੜਿਆਂ ਤੋਂ
ਕਾਲਪਨਿਕ ਮੱਧਮਾਨ (a) = 17
ਸੂਤਰ ਦਾ ਪ੍ਰਯੋਗ ਕਰਨ ‘ਤੇ, ਮੱਧਮਾਨ (\(\bar{X}\)) = a + \(\frac{\Sigma f_{i} d_{i}}{\Sigma f_{i}}\)
\(\bar{X}\) = 17 + \(\frac{(-181)}{40}\)
= 17 – 4.52 = 12.48
∴ ਇੱਕ ਵਿਦਿਆਰਥੀ ਜਿੰਨੇ ਦਿਨ ਗ਼ੈਰ ਹਾਜ਼ਰ ਰਿਹਾ 12.48 ਹੈ ।
![]()
ਪ੍ਰਸ਼ਨ 9.
ਹੇਠਾਂ ਦਿੱਤੀ ਸਾਰਣੀ 35 ਸ਼ਹਿਰਾਂ ਦੀ ਸਾਖਰਤਾ ਦਰ (ਪ੍ਰਤੀਸ਼ਤ ਵਿੱਚ) ਦਰਸਾਉਂਦੀ ਹੈ । ਮੱਧਮਾਨ ਸਾਖਰਤਾ ਦਰ ਪਤਾ ਕਰੋ :

ਹੱਲ:
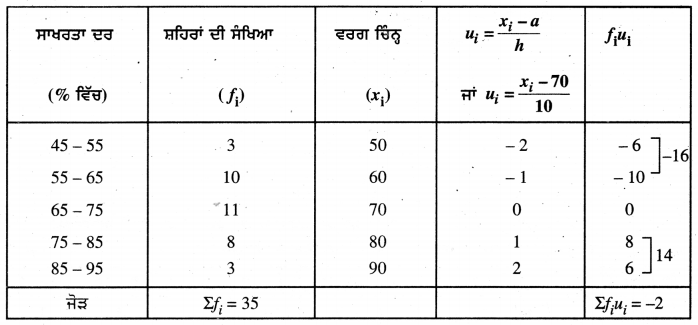
ਉਪਰੋਕਤ ਅੰਕੜਿਆਂ ਤੋਂ
ਕਾਲਪਨਿਕ ਮੱਧਮਾਨ (a) = 70
ਵਰਗ ਮਾਪ (h) = 10
\(\bar{u}\) = \(\frac{\Sigma f_{i} u_{i}}{\Sigma f_{i}}\) = \(\frac{-2}{35}\) = -0.057
ਸੂਤਰ ਦਾ ਪ੍ਰਯੋਗ ਕਰਨ ‘ਤੇ, (\(\bar{X}\)) = a + h\(\bar{u}\)
\(\bar{X}\) = 70 + 10(-0.057)
= 70 – 0.57 = 69.43
ਮੱਧਮਾਨ ਸਾਖਰਤਾ ਦਰ 69.43% ਹੈ ।
