PSEB 10th Class Maths Solutions Chapter 14 ਅੰਕੜਾਵਿਗਿਆਨ Ex 14.2

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 14 ਅੰਕੜਾਵਿਗਿਆਨ Ex 14.2 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 10 Maths Chapter 14 ਅੰਕੜਾਵਿਗਿਆਨ Exercise 14.2

ਪ੍ਰਸ਼ਨ 1.
ਹੇਠ ਦਿੱਤੀ ਸਾਰਣੀ ਕਿਸੇ ਹਸਪਤਾਲ ਵਿੱਚ ਇੱਕ ਵਿਸ਼ੇਸ਼ ਸਾਲ ਵਿੱਚ ਭਰਤੀ ਹੋਏ ਰੋਗੀਆਂ ਦੀ ਉਮਰ ਨੂੰ ਦਰਸਾਉਂਦੀ ਹੈ :

ਉਪਰੋਕਤ ਅੰਕੜਿਆਂ ਦਾ ਬਹੁਲਕ ਅਤੇ ਮੱਧਮਾਨ ਪਤਾ ਕਰੋ । ਦੋਨਾਂ ਕੇਂਦਰੀ ਪ੍ਰਵਿਰਤੀ ਦੇ ਮਾਪਾਂ ਦੀ ਤੁਲਨਾ ਕਰੋ ਅਤੇ ਉਹਨਾਂ ਦੀ ਵਿਆਖਿਆ ਕਰੋ ।
ਹੱਲ:
ਬਹੁਲਕ ਦੇ ਲਈ
ਦਿੱਤੇ ਗਏ ਅੰਕੜਿਆਂ ਵਿੱਚ ਅਧਿਕਤਮ ਬਾਰੰਬਾਰਤਾ 23 ਹੈ ਅਤੇ ਇਸਦੇ ਸੰਗਤ ਵਰਗ ਅੰਤਰਾਲ 35 – 45 ਹੈ :
∴ ਬਹੁਲਕ ਵਰਗ = 35 – 45
ਇਸ ਲਈ l = 35 ; f₁ = 23 ; f₀ = 21; f₂ = 14 ਅਤੇ h = 10
ਸੂਤਰ ਦਾ ਪ੍ਰਯੋਗ ਕਰਨ ‘ਤੇ,
ਬਹੁਲਕ = 1 + (\(\frac{f_{1}-f_{0}}{2 f_{1}-f_{0}-f_{2}}\)) × h
= 35 + [latex]\frac{23-21}{2(23)-21-14}[/latex] × 10
= 35 + \(\frac{2}{46-35}\) × 10
= 35 + \(\frac{20}{11}\) = 35 + 1.8 = 36.8
ਮੱਧਮਾਨ ਲਈ

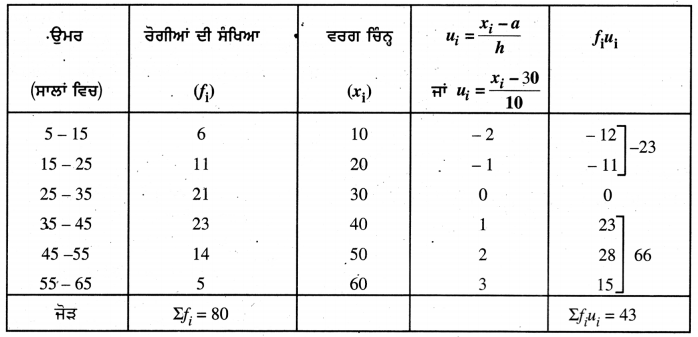
ਉਪਰੋਕਤ ਅੰਕੜਿਆਂ ਤੋਂ
ਕਾਲਪਨਿਕ ਮੱਧਮਾਨ (a) = 30
ਵਰਗ ਮਾਪ (h) = 10
∴ \(\bar{u}\) = \(\frac{\Sigma f_{i} u_{i}}{\Sigma f_{i}}\) = \(\frac{43}{80}\) = 0.5375
ਸੂਤਰ ਦੇ ਪ੍ਰਯੋਗ ਕਰਨ ‘ਤੇ ਬਹੁਲਕ (\(\bar{X}\)) = a + h\(\bar{u}\)
\(\bar{X}\) = 30 + 10(0.5375)
= 30 + 5.375
= 35.375 = 35.37
ਹਸਪਤਾਲ ਵਿਚ ਭਰਤੀ ਰੋਗੀਆਂ ਦੀ ਮੱਧਮਾਨ ਉਮਰ 35.37 ਸਾਲ ਅਤੇ ਅਧਿਕਤਰ ਰੋਗੀਆਂ ਦੀ ਉਮਰ 36.8 ਸਾਲ ਹੈ ।

ਪ੍ਰਸ਼ਨ 2.
ਹੇਠਾਂ ਦਿੱਤੇ ਅੰਕੜੇ, 225 ਬਿਜਲੀ ਉਪਕਰਨਾਂ ਦੇ ਜੀਵਨ ਕਾਲ (ਘੰਟਿਆਂ ਵਿੱਚ) ਦੀ ਸੂਚਨਾ ਦਿੰਦੇ ਹਨ :

ਉਪਕਰਨਾਂ ਦਾ ਬਹੁਲਕ ਜੀਵਨਕਾਲ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਦਿੱਤੇ ਗਏ ਅੰਕੜਿਆਂ ਵਿੱਚ
ਅਧਿਕਤਮ ਬਾਰੰਬਾਰਤਾ 61 ਹੈ ਅਤੇ ਇਸ ਦਾ ਸੰਗਤ ਵਰਗ ਅੰਤਰਾਲ 60 – 80 ਹੈ ।
∴ ਬਹੁਲਕ ਵਰਗ = 60 – 80
∴ l = 60; f₁ = 61 ; f₀ = 52; f₂ = 38 ਅਤੇ h = 20
ਸੂਤਰ ਦਾ ਪ੍ਰਯੋਗ ਕਰਨ ‘ਤੇ
ਬਹੁਲਕ = l + (\(\frac{f_{1}-f_{0}}{2 f_{1}-f_{0}-f_{2}}\)) × h
= 60 + (\(\frac{61-52}{2(61)-52-38}\)) × 20
= 60 + \(\frac{9}{122-52-38}\) × 20
= 60 + \(\frac{9}{32}\) × 20
= 60 + \(\frac{180}{32}\) = 60 +5.625 = 65.625
∴ ਉਪਕਰਣਾਂ ਦਾ ਬਹੁਲਕ ਜੀਵਨਕਾਲ = 65.625 ਘੰਟੇ

ਪ੍ਰਸ਼ਨ 3.
ਹੇਠਾਂ ਦਿੱਤੇ ਅੰਕੜੇ ਕਿਸੇ ਪਿੰਡ ਦੇ 200 ਪਰਿਵਾਰਾਂ ਦੀ ਕੁੱਲ ਮਹੀਨਾਵਾਰ ਘਰੇਲੂ ਖ਼ਰਚ ਦੀ ਵੰਡ ਨੂੰ ਦਰਸਾਉਂਦੇ ਹਨ । ਇਨ੍ਹਾਂ ਪਰਿਵਾਰਾਂ ਦਾ ਬਹੁਲਕ ਮਹੀਨਾਵਾਰ ਖ਼ਰਚ ਪਤਾ ਕਰੋ । ਇਸਦੇ ਨਾਲ ਹੀ ਮੱਧਮਾਨ ਮਹੀਨਾਵਾਰ ਖ਼ਰਚ ਵੀ ਪਤਾ ਕਰੋ ।

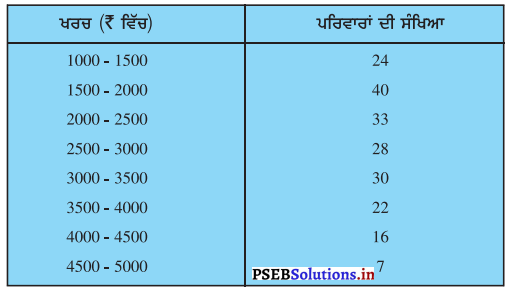
ਹੱਲ:
ਬਹੁਲਕ ਲਈ
ਦਿੱਤੇ ਗਏ ਅੰਕੜਿਆਂ ਦੀ ਅਧਿਕਤਮ ਬਾਰੰਬਾਰਤਾ 40 ਹੈ ਅਤੇ ਸੰਗਤ ਵਰਗ 1500 – 2000 ਹੈ ।
∴ ਬਹੁਲਕ ਵਰਗ = 1500 – 2000
∴ l = 1500 ; f₁ = 40 ; f₀ = 24 ; f₂ = 33 ਅਤੇ h = 500
ਸੂਤਰ ਦਾ ਪ੍ਰਯੋਗ ਕਰਦੇ ਹੋਏ,

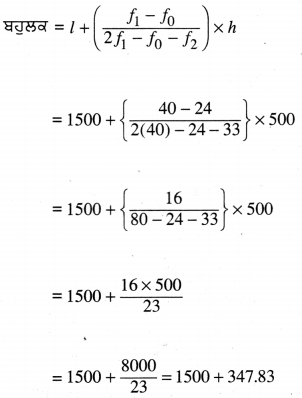
= ₹ 1847.83
ਮੱਧਮਾਨ ਲਈ

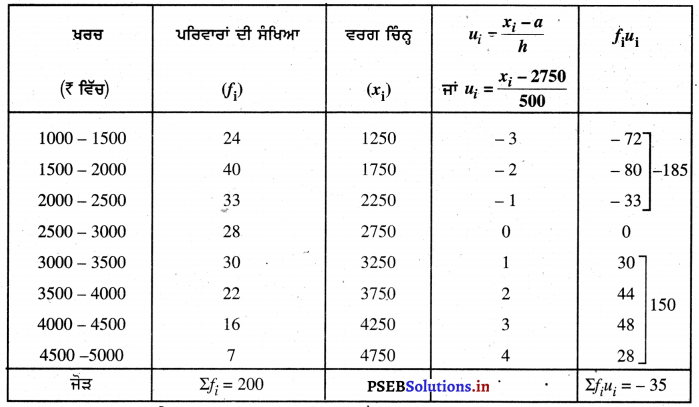
ਕਾਲਪਨਿਕ ਮੱਧਮਾਨ (a)= 2750
ਵਰਗ ਮਾਪ (h) = 500
∴ \(\bar{u}\) = \(\frac{\Sigma f_{i} u_{i}}{\Sigma f_{i}}\) = \(-\frac{35}{200}\) = -0.175
ਸੂਤਰ ਦਾ ਪ੍ਰਯੋਗ ਕਰਨ ‘ਤੇ (\(\bar{X}\)) = a + h\(\bar{u}\)
\(\bar{X}\) = 2750 + 500 (0.175) = 2750 – 87.50
ਪਰਿਵਾਰਾਂ ਦਾ ਮਹੀਨਾਵਾਰ ਬਹੁਲਕ ਖਰਚ ₹ 1847.83
ਅਤੇ ਮਹੀਨਾਵਾਰ ਮੱਧਮਾਨ ਖਰਚ = ₹ 2662.50 ਹੈ

ਪ੍ਰਸ਼ਨ 4.
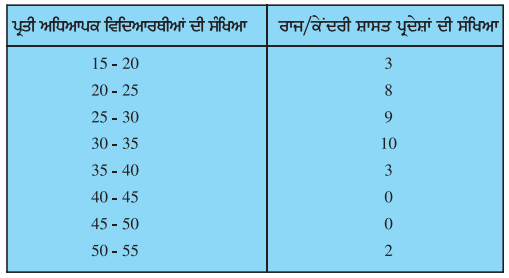
ਹੇਠ ਦਿੱਤੀ ਵੰਡ ਸਾਰਣੀ ਭਾਰਤ ਦੇ ਸੈਕੰਡਰੀ ਸਕੂਲਾਂ ਵਿੱਚ ਰਾਜਾਂ ਅਨੁਸਾਰ, ਅਧਿਆਪਕ-ਵਿਦਿਆਰਥੀ ਅਨੁਪਾਤ ਨੂੰ ਦਰਸਾਉਂਦੀ ਹੈ । ਇਨ੍ਹਾਂ ਅੰਕੜਿਆਂ ਦਾ ਬਹੁਲਕ ਅਤੇ ਮੱਧਮਾਨ ਪਤਾ ਕਰੋ । ਦੋਨਾਂ ਮਾਪਾਂ ਦੀ ਵਿਆਖਿਆ ਕਰੋ ।

ਹੱਲ:
ਬਹੁਲਕ ਲਈ
ਦਿੱਤੇ ਗਏ ਅੰਕੜਿਆਂ ਵਿਚ ਅਧਿਕਤਮ ਬਾਰੰਬਾਰਤਾ 10
ਹੈ ਅਤੇ ਸੰਗਤ ਵਰਗ ਅੰਤਰਕਾਲ 30 – 35 ਹੈ ।
∴ ਬਹੁਲਕ ਵਰਗ = 30 – 35.
∴ l = 30; f₁ = 10 ; f₀ = 9; f₂ = 3 ਅਤੇ h = 5
ਸੂਤਰ ਦੀ ਵਰਤੋਂ ਕਰਨ ‘ਤੇ
ਬਹੁਲਕ = l + (\(\frac{f_{1}-f_{0}}{2 f_{1}-f_{0}-f_{2}}\)) × h
ਬਹੁਲਕ = 30 + (\(\frac{10-9}{2(10)-9-3}\)) × 5
= 30 + \(\frac{1}{20-12}\) × 5
= 30 + \(\frac{5}{8}\) = 30 + 0.625
= 30.625 = 30.63 ਲਗਭਗ
ਮੱਧਮਾਨ ਲਈ

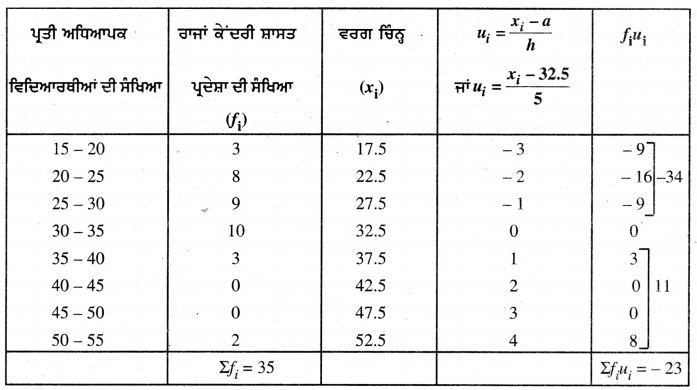
ਉਪਰੋਕਤ ਅੰਕੜਿਆਂ ਤੋਂ
ਕਾਲਪਨਿਕ ਮੱਧਮਾਨ (a) = 32.5
ਵਰਗ ਮਾਪ (h) = 5
∴ \(\bar{u}\) = \(\frac{\Sigma f_{i} u_{i}}{\Sigma f_{i}}\) = \(-\frac{23}{35}\) = – 0.65
ਸੂਤਰ ਦਾ ਪ੍ਰਯੋਗ ਕਰਨ ‘ਤੇ
ਮੱਧਮਾਨ ( \(\bar{X}\)) = a + h\(\bar{u}\)
\(\bar{X}\) = 32.5 + 5(0.65) = 32.5 – 3.25 = 29.25 (ਲਗਭਗ)
∴ ਦਿੱਤੇ ਅੰਕੜਿਆਂ ਦਾ ਬਹੁਲਕ 30.63 ਅਤੇ ਮੱਧਮਾਨ 29.25 ਹੈ ।

ਪ੍ਰਸ਼ਨ 5.
ਦਿੱਤੀ ਹੋਈ ਵੰਡ ਸਾਰਣੀ ਵਿਸ਼ਵ ਦੇ ਕੁੱਝ ਵਧੀਆਂ ਬੱਲੇਬਾਜਾਂ ਦੁਆਰਾ ਇੱਕ ਰੋਜ਼ਾ ਅੰਤਰਰਾਸ਼ਟਰੀ ਕ੍ਰਿਕਟ ਮੈਚਾਂ ਵਿੱਚ ਬਣਾਈਆ ਗਈਆਂ ਦੌੜਾਂ ਨੂੰ ਦਰਸਾਉਂਦੀ ਹੈ :

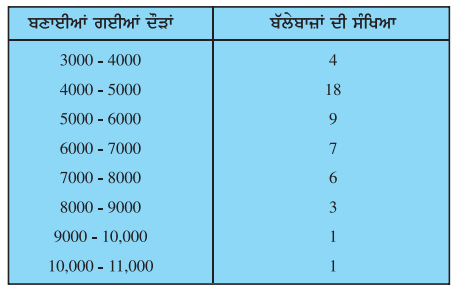
ਇਹਨਾਂ ਅੰਕੜਿਆਂ ਦਾ ਬਹੁਲਕ ਤਾਂ ਕਰੋ ।
ਹੱਲ:
ਦਿੱਤੇ ਗਏ ਅੰਕੜਿਆਂ ਤੋਂ
ਅਧਿਕਤਮ ਬਾਰੰਬਾਰਤਾ 18 ਹੈ ਅਤੇ ਸੰਗਤ ਵਰਗ ਅੰਤਰਾਲ 4000 – 5000 ਹੈ ।
∴ ਬਹੁਲਕ ਵਰਗ = 4000 – 5000
∴ l = 4000; f₁ = 18; f₀ = 4; f₂ = 9 ਅਤੇ h = 1000
ਸੂਤਰ ਦਾ ਪ੍ਰਯੋਗ ਕਰਕੇ ਬਹੁਲਕ
= l + (\(\frac{f_{1}-f_{0}}{2 f_{1}-f_{0}-f_{2}}\)) × h
= 4000 + (\(\frac{18-4}{2(18)-4-9}\)) × 1000
= 4000 + \(\frac{14}{36-13}\) × 1000
= 4000 + \(\frac{14000}{23}\) = 4000 + 608.6956
= 4000 + 608.7 = 4608.7 ਲਗਭਗ
∴ ਇਸ ਲਈ ਦਿੱਤੇ ਗਏ ਅੰਕੜਿਆਂ ਦਾ ਬਹੁਲਕ = 4608.7

ਪ੍ਰਸ਼ਨ 6.
ਇੱਕ ਵਿਦਿਆਰਥੀ ਨੇ ਸੜਕ ਦੇ ਕਿਸੇ ਸਥਾਨ ਉੱਪਰ | ਖੜੇ ਹੋ ਕੇ ਉੱਥੋਂ ਲੰਘਣ ਵਾਲੀਆਂ ਕਾਰਾਂ ਦੀ ਸੰਖਿਆ | ਨੋਟ ਕੀਤੀ ਅਤੇ ਉਹਨਾਂ ਨੂੰ ਹੇਠ ਦਿੱਤੀ ਸਾਰਣੀ ਦੇ ਰੂਪ ਵਿੱਚ ਪ੍ਰਗਟ ਕੀਤਾ । ਸਾਰਣੀ ਵਿਚ ਹਰੇਕ ਪ੍ਰੇਖਣ 3 ਮਿੰਟ ਦੇ ਅੰਤਰਾਲ ਨਾਲ ਉਸ ਸਥਾਨ ਤੋਂ ਲੰਘਣ ਵਾਲੀਆਂ | ਕਾਰਾਂ ਦੀ ਸੰਖਿਆ ਨਾਲ ਸੰਬੰਧਿਤ ਹੈ । ਇਹੋ ਜਿਹੇ 100 | ਅੰਤਰਾਲਾਂ ਉੱਪਰ ਪ੍ਰੇਖਣ ਲਏ ਗਏ । ਇਹਨਾਂ ਅੰਕੜਿਆਂ ਦਾ ਬਹੁਲਕ ਪਤਾ ਕਰੋ ।

ਹੱਲ:
ਦਿੱਤੇ ਗਏ ਅੰਕੜਿਆਂ ਵਿਚ
ਅਧਿਕਤਮ ਬਾਰੰਬਾਰਤਾ 20 ਹੈ ਅਤੇ ਸੰਗਤ ਵਰਗ ਅੰਤਰਾਲ 40 – 50 ਹੈ ।
ਬਹੁਲਕ ਵਰਗ = 40 – 50
l = 40 ; f₁ = 20 ; f₀ = 12 ; f₂ = 11 ਅਤੇ h= 10
ਸਤਰ ਦਾ ਪ੍ਰਯੋਗ ਕਰਨ ‘ਤੇ ਬਹੁਲਕ = l + (\(\frac{f_{1}-f_{0}}{2 f_{1}-f_{0}-f_{2}}\)) × h
ਬਹੁਲਕ = 40 +(\(\frac{20-12}{2(20)-12-11}\)) × 10
= 40 + \(\frac{8}{40-23}\) × 10
= 40 + \(\frac{80}{17}\) = 40 + 4.70588
= 40 + 4.7 = 44.7 (ਲਗਭਗ)
∴ ਇਸ ਲਈ ਦਿੱਤੇ ਅੰਕੜਿਆਂ ਦਾ ਬਹੁਲਕ = 44.7