Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 14 सांख्यिकी Ex 14.3 Textbook Exercise Questions and Answers
PSEB Solutions for Class 10 Maths Chapter 14 सांख्यिकी Ex 14.3
प्रश्न 1.
निम्नलिखित बारंबारता बंटन किसी मोहल्ले के 68 उपभोक्ताओं की बिजली कर मासिक खपत दर्शाता है। इन आंकड़ों के माध्यक, माध्य और बहुलक ज्ञात कीजिए। इनकी तुलना कीजिए।
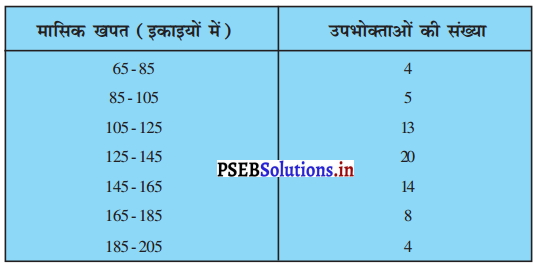
हल:
माध्यक के लिए:
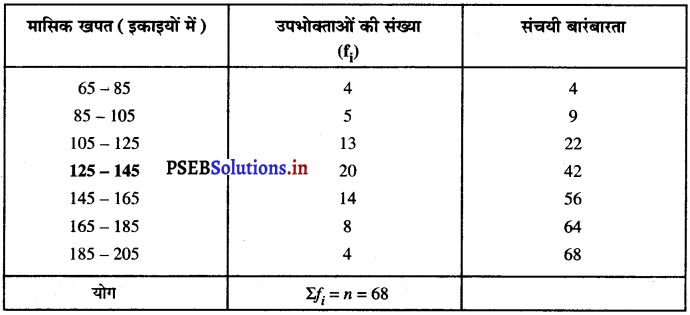
यहाँ, Σfi = n = 68 तो \(\frac{n}{2}=\frac{68}{2}\) = 34
जो कि वर्ग अतंराल 125 – 145 में स्थित है।
∴ माध्यक वर्ग = 125 – 145
अतः,l = 125; n = 68; f = 20 ; cf = 22 और h = 20
सूत्र का प्रयोग करने पर, माध्यक = l + \(\left[\frac{\frac{n}{2}-c f}{f}\right]\) × h
= 25 + \(\left\{\frac{\frac{68}{2}-22}{20}\right\}\) × 20
= 125 + \(\frac{34-22}{20}\) × 20
= 125 + 12 = 137
माध्य के लिए:
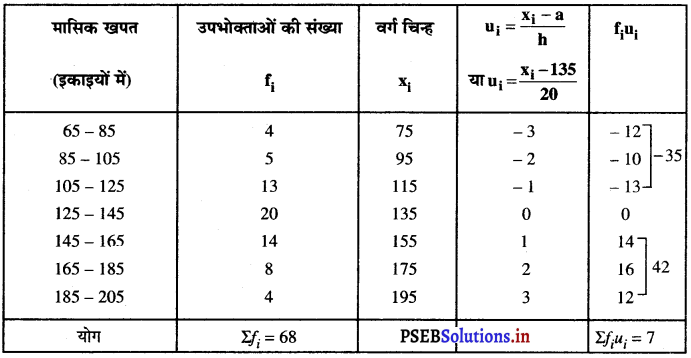
उपरोक्त आँकड़ों से, कल्पित मान (a) = 135
वर्ग माप (h) = 20
∴ \(\bar{u}=\frac{\Sigma f_{i} u_{i}}{\Sigma f_{i}}=\frac{7}{68}\) = 0.102
सूत्र का प्रयोग करने पर, माध्य \((\overline{\mathrm{X}})=a+h \bar{u}\)
\(\overline{\mathrm{X}}\) = 135 + 20 (0.102)
= 135 + 2.04 = 137.04
बहुलक के लिए: दिए गए आँकड़ों में अधिकतम बारंबारता 20 है और इसके संगत वर्ग 125 – 145 है
∴ बहुलक वर्ग = 125 – 145
इसलिए,
l = 125; f = 20; f = 13; f = 14 और h = 20
सूत्र का प्रयोग करने पर, बहुलक = l + \(\left(\frac{f_{1}-f_{0}}{2 f_{1}-f_{0}-f_{2}}\right)\)
बहुलक = 125 + \(\left(\frac{20-13}{2(20)-13-14}\right)\) x 20
= 125 +\(\frac{7}{40-27}\) x 20
= 125 + \(\frac{140}{13}\)
= 125 + 10.76923
= 125 + 10.77 = 135.77.
अतः दिए गए आंकड़ों का माध्यक, माध्य और बहुलक है : 137 मात्रक, 137.04 मात्रक और 135.77 मात्रक।
![]()
प्रश्न 2.
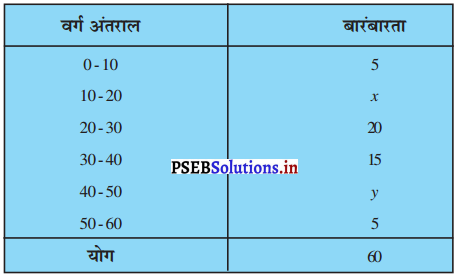
यदि नीचे दिए हुए बंटन का माध्यक 28.5 हो, तो x और y के मान ज्ञात कीजिए :
हल:
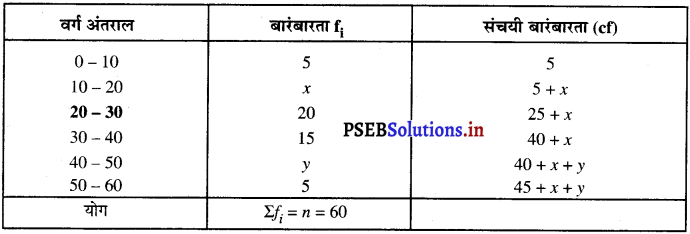
दिए गए आंकड़ों में, if Σfi = n = 60
∴ \(\frac{n}{2}=\frac{60}{2}\) = 30
साथ ही, बंटन का माध्यक = 28.5 …………(दिया है)
जोकि वर्ग अंतराल 20 – 30 में स्थित है।
∴ माध्यक वर्ग = 20 – 30
इसलिए, l = 20 ; f = 20 ; cf = 5 + x ; h = 10
सारणी से यह स्पष्ट है कि 45 + x + y = 60
x + y = 60 – 45 = 15
य x + y = 15 …………….(1)
अब, सूत्र का प्रयोग करने पर
माध्यक = l + \(\left\{\frac{\frac{n}{2}-c f}{f}\right\}\) × h
28.5 = 20 + \(\left\{\frac{30-(5+x)}{20}\right\}\) × 10
28.5 = 20 + \(\frac{30-5-x}{2}\)
28.5 = \(\frac{40+25-x}{2}\)
2(28.5) = 65 – x
57.0 = 65- x
x = 65 – 57 = 8
∴ x = 8
x के इस मान को (1) में प्रतिस्थापित करने पर हमें प्राप्त होता है,
8 + y = 15
y = 15 – 8 = 7
अतः, x और y के मान 8 और 7 हैं।
![]()
प्रश्न 3.
एक जीवन बीमा एजेंट 100 पॉलिसी धारकों की आयु में बंटन के निम्नलिखित आंकड़ें ज्ञात करता है। माध्यक आयु परिकलित कीजिए, यदि पॉलिसी केवल उन्हीं व्यक्तियों को दी जाती है, जिनकी आयु 18 वर्ष या उससे अधिक हो, परंतु 60 वर्ष से कम हो।
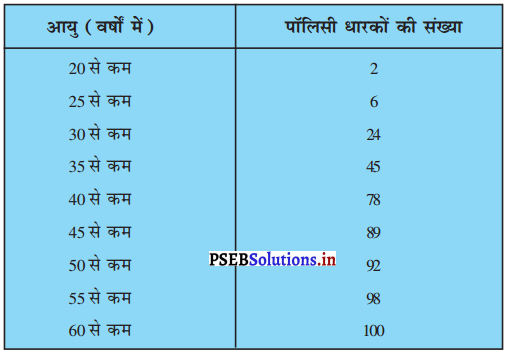
हल:
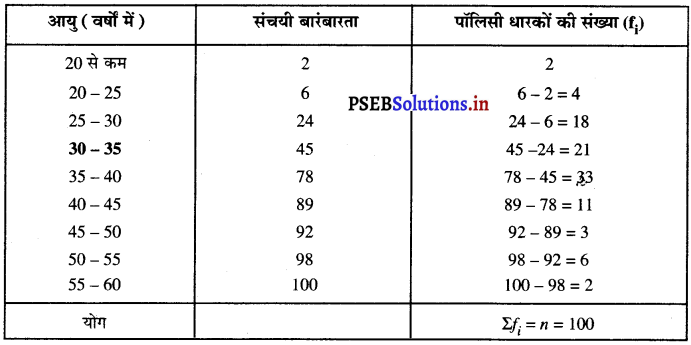
यहाँ, Σfi = n = 100
तो, \(\frac{n}{2}=\frac{100}{2}\) = 50,
जोकि अंतराल 35 – 40 में स्थित है।
∴ माध्यक वर्ग = 35 – 40
इसलिए,
1 = 35 ; n = 100 ; f = 33 ; cf = 45 और h = 5
सूत्र का प्रयोग करने पर,
माध्यक = l + \(\left\{\frac{\frac{n}{2}-c f}{f}\right\}\) × h
= 35 + \(\left\{\frac{\frac{100}{2}-45}{33}\right\}\) × 5
= 35 + \(\frac{50-45}{33}\) × 5
= 35 + \(\frac{25}{33}\)
= 35 + 0.7575
= 35 + 0.76 (लगभग)
= 35.76
अतः, दिए गए आंकड़ों की माध्यक आयु 35.76 वर्ष है।
![]()
प्रश्न 4.
एक पौधे की 40 पत्तियों की लंबाईयाँ निकटतम मिली मीटरों में मापी जाती है तथा प्राप्त आंकड़ों को निम्नलिखित सारणी के रूप में निरुपित किया जाता है :
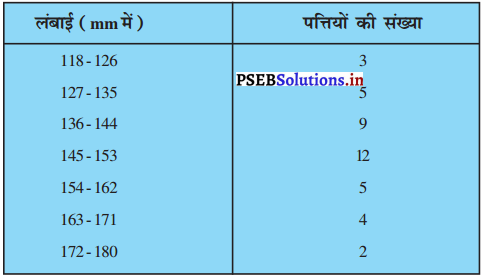
पत्तियों की माध्यक लंबाई ज्ञात कीजिए।
हल :
क्योंकि बारंबारता बंटन लगातार नहीं है हम इसे पहले लगातार बंटन में परिवर्तित करेंगे

यहाँ, Σfi = n = 40 Ef=n = 40 n 40
तो \(\frac{n}{2}=\frac{40}{2}\) = 20,
जो कि अंतराल 144.5 – 153.5 में स्थित है।
∴ माध्यक वर्ग = 144.5 – 153.5
इसलिए,
l = 144.5 ; f = 12 ; cf = 17; h = 9
सूत्र का प्रयोग करने पर,
माध्यक = l + \(\left\{\frac{\frac{n}{2}-c f}{f}\right\}\) × h
माध्यक = 144.5 + \(\left\{\frac{20-17}{12}\right\}\) × 9
= 144.5 + \(\frac{3 \times 9}{12}\)
= 144.5 + 2.25 = 146.75
अतः, पत्तियों की माध्यक लंबाई 146.75 mm है।
![]()
प्रश्न 5.
निम्नलिखित सारणी 400 नियॉन लैंपों के जीवन कालों (life time) को प्रदर्शित करती है : जीवन काल (घंटों में)
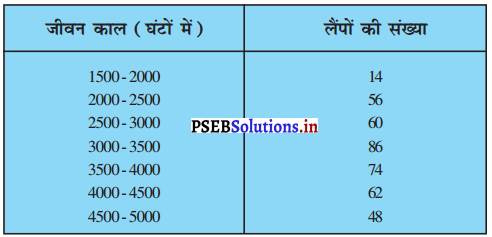
एक लैंप का माध्यक जीवन काल ज्ञात कीजिए। पत्तियों की माध्यक लंबाई ज्ञात कीजिए।
हल :
क्योंकि बारंबारता बंटन लगातार नहीं है हम इसे पहले लगातार बंटन में परिवर्तित करेंगे
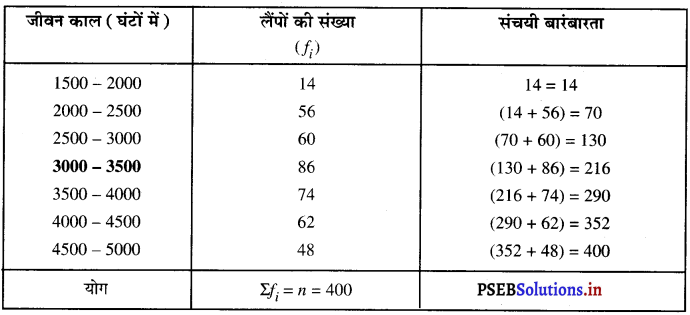
यहाँ, Σfi = n = 40
∴ तो, \(\frac{n}{2}=\frac{40}{2}\) = 20,
जो कि अंतराल 3000 – 3500 में स्थित है।
∴ माध्यक वर्ग = 3000 – 3500
इसलिए, l = 3000 ; n = 400 ; f = 86 ; cf = 130 और h = 500
सूत्र का प्रयोग करने पर, माध्यक वगई = l + \(\left\{\frac{\frac{n}{2}-c f}{f}\right\}\) × h
माध्यक = 3000 + \(\left\{\frac{\frac{400}{2}-130}{86}\right\}\) × 500
= 3000 + \(\left(\frac{200-130}{86}\right)\) × 500
= 3000 + \(\frac{70 \times 500}{86}\)
= 3000 + 406.9767441
= 3000 + 406.98 (लगभग) = 3406.98
अतः, लेंप का जीवन काल 3406.98 घंटे है।
![]()
प्रश्न 6.
एक स्थानीय टेलीफोन निर्देशिका से 100 कुल नाम (surnames) लिए गए उनमें प्रयुक्त अंग्रेज़ी वर्णमाला के अक्षरों की संख्या का निम्नलिखित बारंबारता बंटन प्राप्त हुआ :

हल:
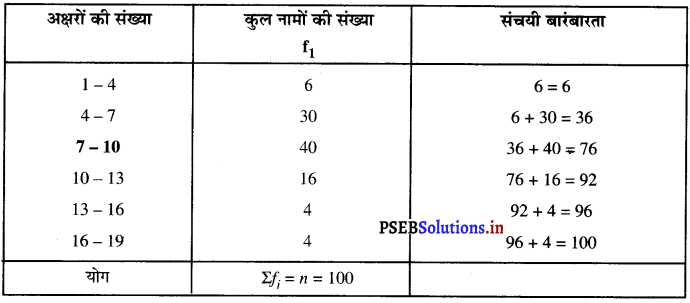
Σfi = n = 100
∴ \(\frac{n}{2}=\frac{100}{2}\) = 50
जोकि अंतराल 7 – 10 में स्थित है।
∴ माध्यक वर्ग = 7 – 10
इसलिए,
l = 7; n = 100 ; f = 40 ; cf = 36 और h = 3
सूत्र का प्रयोग करने पर, माध्यक = l + \(\left\{\frac{\frac{n}{2}-c f}{f}\right\}\) × h
माध्यक = 7 + \(\left\{\frac{\frac{100}{2}-36}{40}\right\}\) × 3
= 7 + \(\left\{\frac{50-36}{40}\right\}\) × 3
= 7 + \(\frac{14 \times 3}{40}\)
= 7 + \(\frac{21}{20}\)
= 7 + 1.05 = 8.05
अतः, माध्यक अक्षरों की संख्या 8.05 है।
माध्य के लिए:
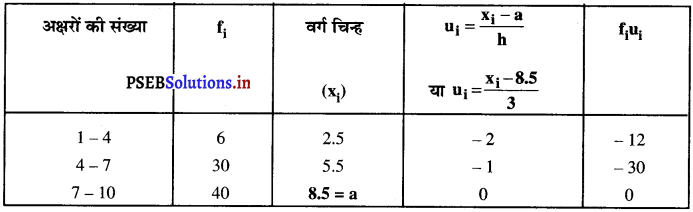

उपरोक्त आँकड़ों से, कल्पित माध्य (a) = 8.5
वर्ग माप (h) = 3
∴ \(\bar{u}=\frac{\Sigma f_{i} u_{i}}{\Sigma f_{i}}=\bar{u}=\frac{-6}{100}\) = – 0.06
सूत्र का प्रयोग करने पर,
माध्यक \((\bar{x})=a+h \bar{u}\)
\(\bar{x}\) = 8.5 + 3 (- 0.06)
= 8.5 – 0.18 = 8.32
अतः, कुल नामों में माध्य अक्षरों की संख्या 8.32 अक्षर है।
![]()
बहुलक के लिए :
दिए गए आँकड़ों में अधिकतम बारंबारता 40 है और इसका संगत अंतराल 7 – 10 है।
∴ बहुलक वर्ग = 7 – 10
इसलिए,
l = 7; f1 = 40 ; f0 = 30 ; f2 = 16 और h = 3
सूत्र का प्रयोग करने पर,
बहुलक = l + \(\left(\frac{f_{1}-f_{0}}{2 f_{1}-f_{0}-f_{2}}\right)\) × h
बहुलक = 7 + \(\left(\frac{40-30}{2(40)-30-16}\right)\) × 3
= 7 + \(\frac{10}{80-46}\) × 3
= 7 + \(\frac{30}{34}\)
= 7 + 0.882352941
= 7 + 0.88 (लगभग) = 7.88
अतः, कुलनामों का बहुलक माप 7.88 अक्षर है।
प्रश्न 7.
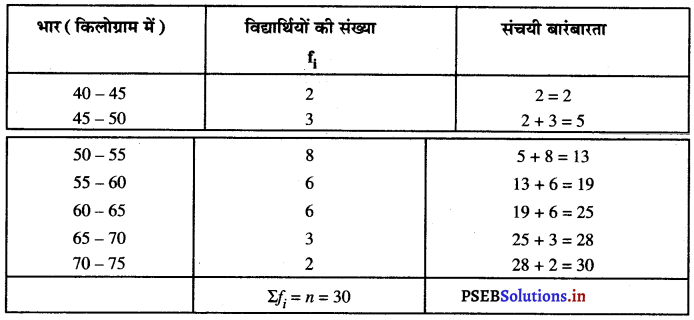
नीचे दिया हुआ बंटन एक कक्षा के 30 विद्यार्थियों के भार दर्शा रहा है। विद्यार्थियों का माध्यक भार ज्ञात कीजिए:

हल:
![]()
यहाँ Σfi = n = 30
∴ \(\frac{n}{2}=\frac{30}{2}\) = 15;
जोकि अंतराल 55 – 60 में स्थित है।
∴ माध्यक वर्ग = 55 – 60
इसलिए, n = 30; f = 6; cf = 13 और h = 5
सूत्र का प्रयोग करने पर, माध्यक = l + \(\left\{\frac{\frac{n}{2}-c f}{f}\right\}\) × h
माध्यक = 55 + \(\left\{\frac{\frac{30}{2}-13}{6}\right\}\) × 5
= 55 + \(\left\{\frac{15-13}{6}\right\}\) × 5
= 55 + \(\frac{2 \times 5}{6}\)
माध्यक = 55 + \(\frac{5}{3}\)
= 55 + 1.66666
= 55 + 1.67 लगभग = 56.67
अतः, माध्यक भार 56.67 किलोग्राम है।
