PSEB 10th Class Maths Solutions Chapter 14 सांख्यिकी Ex 14.4

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 14 सांख्यिकी Ex 14.4 Textbook Exercise Questions and Answers

PSEB Solutions for Class 10 Maths Chapter 14 सांख्यिकी Ex 14.4

प्रश्न 1.
निम्नलिखित बंटन किसी फैक्टरी के 50 श्रमिकों की दैनिक आय दर्शाता है :

‘उपरोक्त बंटन को एक कम प्रकार’ के संचयी बारंबारता बंटन में बदलिए और उसका तोरण खींचिए।
हल:

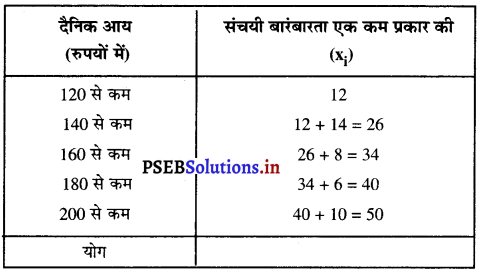
हम हमें बिंदुओं,
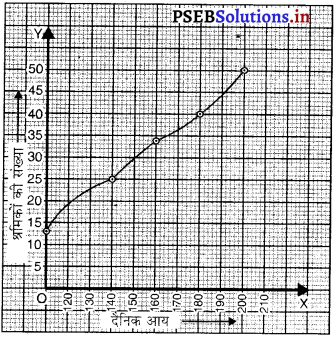
अर्थात् (120, 12); (140, 26) ; (160, 34) ; (180, 40) ; (200, 50) को ग्राफ पेपर पर आलेखित करते हैं। हम एक कम प्रकार के संचय बारंबारता का ग्राफ प्राप्त करते है।
चुना गया पैमाना :
x-अक्ष पर मात्रक 10 मात्रक = रु 10
y-अक्ष 10 मात्रक = 5 श्रमिक

प्रश्न 2.
किसी कक्षा के 35 विद्यार्थियों की मेडिकल जाँच के समय, उनके भार निम्नलिखित में रिकार्ड किए गए :

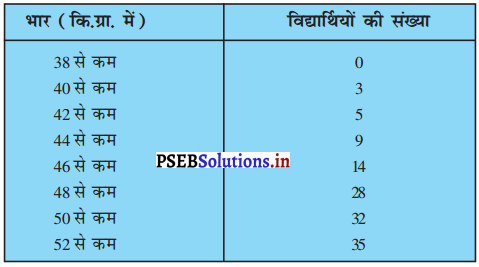
उपरोक्त आँकड़ों के “लिए कम प्रकार का तोरण’ खींचिए। इसके बाद माध्यक भार ज्ञात कीजिए। हल भार विद्यार्थियों की संख्या । वर्ग अंतराल
हल :

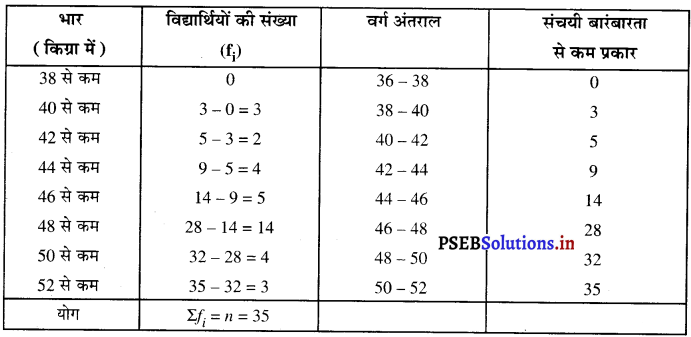
अब, आलेख पर बिंदुओं अर्थात् (38, 0) ; (40, 3) ; (42, 5) ; (44, 9) ; (46, 14); (48, 28); (50, 32); (52, 35) आलेखित करने पर हमें से कम प्रकार की संचयी बारंबारता बहुभज प्राप्त होता है।
चुना गया पैमाना :
x-अक्ष पर, 10 मात्रक = 2 किग्रा
y-अक्ष पर 10 मात्रक = 5 विद्यार्थी

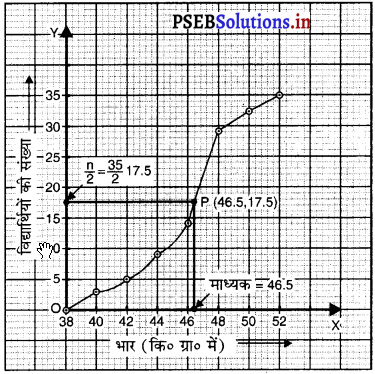
उपरोक्त आलेख से, यह स्पष्ट है कि माध्यक = 46.5 कि ग्रा जोकि अंतराल 46-48 में स्थित है
अब, दी गई सारणी में
Σf_i = n = 35 n 35
∴ \(\frac{n}{2}=\frac{35}{2}\) = 17.5 ;
जोकि अंतराल 46 – 48 में स्थित है।
∴ माध्यक वर्ग = 46 – 48
इसलिए,
l = 46 ; n = 35 ; f= 14 ; cf = 14 और h = 2
सूत्र का प्रयोग करने पर, माध्यक = l + \(\left\{\frac{\frac{n}{2}-c f}{f}\right\}\) × h
माध्यक = 46 + \(\left\{\frac{\frac{35}{2}-14}{14}\right\}\) × 2
= 46 + \(\left\{\frac{\frac{35-28}{2}}{14}\right\}\) × 2
= 46 + \(\frac{7}{2} \times \frac{1}{14}\) × 2
= 46 + \(\frac{1}{2}\)
= 46 + 0.5 = 46.5
उपरोक्त चर्चा और ग्राफ से यह स्पष्ट है कि दोनों स्थितियों में माध्यक एक समान ही है।
अतः, विद्यार्थियों का माध्यक भार 46.5 किग्रा है।

प्रश्न 3.
निम्नलिखित सारणी किसी गाँव के 100 फार्मों में हुआ प्रतिहेक्टेयर (ha) गेहूँ का उत्पादन दर्शाते हैं :

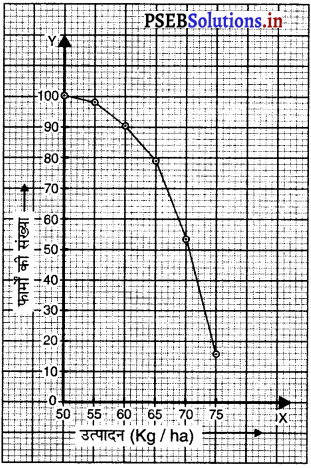
इस बंटन को “अधिक के प्रकार के” बंटन में बदलिए और फिर उसका तोरण खींचिए
हल :

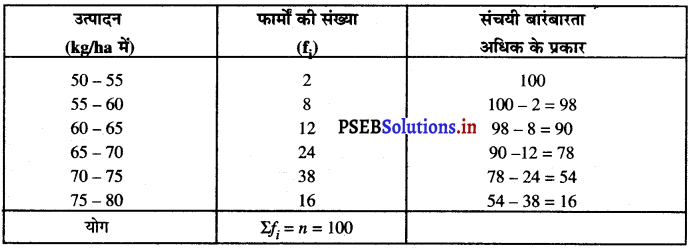
अब, हम बिंदुओं अर्थात् (50, 100) ; (55, 98) ; (60, 90) ; (65, 78); (70, 54); (75, 16) को ग्राफ पेपर पर आलेखित करते हैं।
हम अधिक के प्रकार’ की संचयी बारंबारता का ग्राफ प्राप्त करते हैं।
चुना गया पैमाना:
x-अक्ष पर 10 मात्रक = 5 kg/ha
y-अक्ष पर 10 मात्रक = 10 फार्म