PSEB 10th Class Maths Solutions Chapter 2 ਬਹੁਪਦ Ex 2.2

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 2 ਬਹੁਪਦ Ex 2.2 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 10 Maths Chapter 2 ਬਹੁਪਦ Exercise 2.2

1. ਹੇਠਾਂ ਦਿੱਤੇ ਦੋ ਘਾਤੀ ਬਹੁਪਦਾਂ ਦੇ ਸਿਫ਼ਰ ਪਤਾ ਕਰੋ ਅਤੇ ਸਿਫ਼ਰਾਂ ਅਤੇ ਗੁਣਾਂਕਾਂ ਦੇ ਵਿਚਕਾਰ ਸੰਬੰਧਾਂ ਦੀ ਸੱਚਾਈ ਦੀ ਜਾਂਚ ਕਰੋ :

ਪ੍ਰਸ਼ਨ (i).
x² -2x – 8
ਉੱਤਰ:
ਦਿੱਤੀ ਗਈ ਦੋ ਘਾਤੀ ਬਹੁਪਦ ਹੈ :
x² – 2x -8
|s = – 2
P = 8
= x² – 4x + 2x – 8
= x (x – 4) + 2 (x – 4)
= (x – 4) (x + 2)
x² – 2x – 8 ਦਾ ਮੁੱਲ ਸਿਫ਼ਰ ਹੋਵੇਗਾ
ਜੇਕਰ (x – 4) = 0 ਜਾਂ (x + 2) = 0
x = 4 ਜਾਂ x = – 2
x² – 2x – 8 ਦੇ ਸਿਫ਼ਰ -2 ਅਤੇ 4 ਹਨ ।
ਹੁਣ, ਸਿਫ਼ਰਾਂ ਦਾ ਜੋੜ = (-2) + (4) = 2

ਇਸ ਲਈ ਸਿਫ਼ਰਾਂ ਅਤੇ ਗੁਣਾਂਕਾਂ ਦੇ ਵਿਚ ਸੰਬੰਧਾਂ ਦੀ ਸੱਚਾਈ ਦੀ ਜਾਂਚ ਕੀਤੀ ਜਾਂਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ (ii).
4s² – 4s + 1
ਉੱਤਰ:
ਦਿੱਤਾ ਗਿਆ ਦੋ ਘਾਤੀ ਬਹੁਪਦ ਹੈ
4s² – 4s + 1
= 4s² – 2s – 2s + 1 | S = – 4
= 2s (2s – 1) – 1(2 – 1) | P = 4 × 1 = 4
= (2s – 1) (2s – 1)
4s² – 4s + 1 ਦਾ ਮੁੱਲ ਸਿਫ਼ਰ ਹੋਵੇਗਾ ।
ਜੇਕਰ (2s – 1) = 0 ਜਾਂ (2s – 1) = 0
ਜੇਕਰ s = \(\frac{1}{2}\) ਜਾਂ s = \(\frac{1}{2}\)
ਇਸ ਲਈ, 4s² – 4s + 1 ਦੇ ਸਿਫ਼ਰ \(\frac{1}{2}\) ਅਤੇ \(\frac{1}{2}\)
ਹੁਣ, ਸਿਫ਼ਰਾਂ ਦਾ ਜੋੜ = \(\frac{1}{2}\) + \(\frac{1}{2}\) = 1 = \(\frac{-(-4)}{4}\)

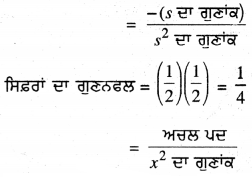
ਇਸ ਲਈ ਸਿਫ਼ਰਾਂ ਅਤੇ ਗੁਣਾਂਕਾਂ ਦੇ ਵਿਚ ਸੰਬੰਧਾਂ ਦੀ ਸਚਾਈ ਦੀ ਜਾਂਚ ਕੀਤੀ ਜਾਂਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ (iii).
6x² – 3 – 7x
ਉੱਤਰ:
ਦਿੱਤੀ ਗਈ ਦੋ ਘਾਤੀ ਬਹੁਪਦ ਹੈ। :
6x² – 3 – 7x
= 6x² – 7x – 3 | S = -7
= 6x² – 9x + 2 – 3 | P = 6 × – 3 = – 18
= 3x (2 – 3) + 1 (2 – 3)
= (2x – 3) (3x + 1)
6x² – 3 – 7x ਦਾ ਮੁੱਲ ਸਿਫ਼ਰ ਹੋਵੇਗਾ ।
ਜੇਕਰ (2x – 3) = 0 ਜਾਂ 3x + 1 = 0
ਜੇਕਰ x = \(\frac{3}{2}\) ਜਾਂ x = \(\frac{-1}{3}\)
ਇਸ ਲਈ, 6x² – 3 – 7x ਦੇ ਸਿਛਰ \(\frac{3}{2}\) ਅਤੇ \(\frac{-1}{3}\) ਹਨ ।


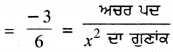
ਇਸ ਲਈ, ਸਿਫ਼ਰਾਂ ਅਤੇ ਗੁਣਾਂਕਾਂ ਦੇ ਵਿਚ ਸੰਬੰਧਾਂ ਦੀ ਸੱਚਾਈ ਦੀ ਜਾਂਚ ਕੀਤੀ ਜਾਂਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ (iv).
4u² + 8u
ਉੱਤਰ:
ਦਿੱਤੀ ਗਈ ਦੋਘਾਤੀ ਬਹੁਪਦ ਹੈ
4u² + 8 = 4u (u + 2)
4u² + 8u ਦਾ ਮੁੱਲ ਸਿਫ਼ਰ ਹੋਵੇਗਾ ।
ਜੇਕਰ 4u = 0 ਜਾਂ u + 2 = 0
ਜੇਕਰ u = 0 ਜਾਂ u = – 2
ਇਸ ਲਈ, 4u² + 8u ਦੇ ਸਿਫ਼ਰ 0 ਅਤੇ – 2 ਹਨ ।
ਹੁਣ ਸਿਫ਼ਰਾਂ ਦਾ ਜੋੜ = 0 + (-2)

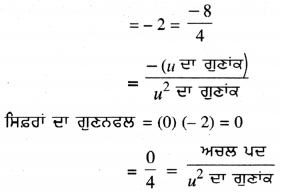
ਇਸ ਲਈ ਸਿਫ਼ਰਾਂ ਅਤੇ ਗੁਣਾਂਕਾਂ ਵਿਚ ਸੰਬੰਧ ਦੀ ਸੱਚਾਈ ਦੀ ਜਾਂਚ ਕੀਤੀ ਜਾਂਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ (v).
t² – 15
ਉੱਤਰ:
ਦਿੱਤੀ ਗਈ ਦੋ ਘਾਤੀ ਬਹੁਪਦ ਹੈ
t² – 15
= t² – (\(\sqrt {15}\))²
= (t- \(\sqrt {15}\)) (t + \(\sqrt {15}\))
t² – 15 ਦਾ ਮੁੱਲ ਸਿਫ਼ਰ ਹੋਵੇਗਾ ।
ਜੇਕਰ t – \(\sqrt {15}\) = 0 ਜਾਂ t +\(\sqrt {15}\) = 0
ਜੇਕਰ t = \(\sqrt {15}\) ਜਾਂ t = –\(\sqrt {15}\)
ਇਸ ਲਈ t² – 15 ਦੇ ਸਿਫ਼ਰ –\(\sqrt {15}\) ਅਤੇ \(\sqrt {15}\) ਹਨ ।
ਹੁਣ ਸਿਫ਼ਰਾਂ ਦਾ ਜੋੜ = –\(\sqrt {15}\) + \(\sqrt {15}\)
= 0 = \(\frac{0}{1}\)

ਇਸ ਲਈ ਸਿਫ਼ਰਾਂ ਅਤੇ ਗੁਣਾਂਕਾਂ ਦੇ ਵਿਚਕਾਰ ਸੰਬੰਧ ਦੀ ਸੱਚਾਈ ਦੀ ਜਾਂਚ ਕੀਤੀ ਜਾਂਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ (vi).
3x² – x – 4
ਉੱਤਰ:
ਦਿੱਤੀ ਗਈ ਦੋ ਘਾਤੀ ਬਹੁਪਦ ਹੈ
3x² – x -4
= 3x² + 3x – 4x – 4 | S = – 1
= 3x(x + 1) – 4(x + 1) | P = 3 × -4 = – 12
= (x + 1) (3x – 4)
3x² – x – 4 ਦਾ ਮੁੱਲ ਸਿਫ਼ਰ ਹੋਵੇਗਾ ।
ਜੇਕਰ (x + 1) = 0 ਜਾਂ 3x – 4 = 0
ਜੇਕਰ x = – 1 ਜਾਂ x = \(\frac{4}{3}\)
ਇਸ ਲਈ, 3x² – x – 4 ਦੇ ਸਿਫ਼ਰ – 1 ਅਤੇ \(\frac{4}{3}\) ਹਨ ।
ਹੁਣ, ਸਿਫ਼ਰਾਂ ਦਾ ਜੋੜ = -1 + \(\frac{4}{3}\)

ਇਸ ਲਈ ਸਿਫ਼ਰਾਂ ਅਤੇ ਗੁਣਾਂਕਾਂ ਵਿਚ ਸੰਬੰਧਾਂ ਦੀ ਸੱਚਾਈ ਦੀ ਜਾਂਚ ਕੀਤੀ ਜਾਂਦੀ ਹੈ ।

2. ਇਕ ਦੋ ਘਾਤੀ ਬਹੁਪਦ ਪਤਾ ਕਰੋ, ਜਿਸਦੇ ਸਿਫ਼ਰਾਂ ਦਾ ਜੋੜ ਅਤੇ ਗੁਣਨਫਲ ਕੁਮਵਾਰ ਦਿੱਤੀਆਂ ਸੰਖਿਆਵਾਂ ਹਨ :

ਪ੍ਰਸ਼ਨ (i).
\(\frac{1}{4}\), -1
ਉੱਤਰ:
ਦਿੱਤੇ ਗਏ ਸਿਫ਼ਰਾਂ ਦਾ ਜੋੜ ਅਤੇ ਸਿਫ਼ਰਾਂ ਦਾ ਗੁਣਨਫਲ \(\frac{1}{4}\) ਅਤੇ -1 ਹੈ ।
ਮੰਨ ਲਉ ਦੋ ਘਾਤੀ ਬਹੁਪਦ ax² + bx + c ਹੈ, ਅਤੇ α ਅਤੇ β ਇਸਦੇ ਸਿਫ਼ਰ ਹਨ ।
∴ α + β = ਸਿਫ਼ਰਾਂ ਦਾ ਜੋੜ = \(\frac{1}{4}\)
ਅਤੇ αβ = ਸਿਫ਼ਰਾਂ ਦਾ ਗੁਣਨਫਲ = – 1
ਇਸ ਲਈ, ax² + bx + c
= k (x – α) (x – β)
ਜਿੱਥੇ k ਕੋਈ ਅਚਲ ਹੈ ।
= k[x² – (α + β)x + αβ]
= k[x² – \(\frac{1}{4}\)x + (-1)]
= k[x² – \(\frac{1}{4}\)x – 1]
k ਦੇ ਵੱਖ-ਵੱਖ ਮੁੱਲਾਂ ਦੇ ਲਈ ਅਸੀਂ ਵੱਖ-ਵੱਖ ਦੋ ਘਾਤੀ ਬਹੁਪਦ ਪ੍ਰਾਪਤ ਕਰਦੇ ਹਾਂ ।

ਪ੍ਰਸ਼ਨ (ii).
\(\sqrt {2}\) , \(\frac{1}{3}\)
ਉੱਤਰ:
ਦਿੱਤੇ ਹੋਏ ਸਿਫ਼ਰਾਂ ਦਾ ਜੋੜ ਅਤੇ ਗੁਣਨਫਲ ਕ੍ਰਮਵਾਰ \(\sqrt {2}\) ਅਤੇ \(\frac{1}{3}\) ਹੈ ।
ਮੰਨ ਲਓ ax² + bx + c ਇਕ ਦੋ ਘਾਤੀ ਬਹੁਪਦ ਹੈ ਅਤੇ α ਅਤੇ β ਇਸ ਦੇ ਸਿਫ਼ਰ ਹਨ ।
α + β = ਸਿਫ਼ਰਾਂ ਦਾ ਜੋੜ = \(\sqrt {2}\)
ਅਤੇ αβ = ਸਿਫ਼ਰਾਂ ਦਾ ਗੁਣਨਫਲ = \(\frac{1}{3}\)
ਹੁਣ, ax² + bx + c = k(x – α) (x – β)
ਇੱਥੇ k ਕੋਈ ਅਚਲ ਹੈ ।
= k[x² – (α + β)x + αβ]
= k[x² – \(\sqrt {2}\)x + \(\frac{1}{3}\)]
k ਦੇ ਵੱਖ-ਵੱਖ ਮੁੱਲਾਂ ਦੇ ਲਈ ਅਸੀ ਵੱਖ-ਵੱਖ ਦੋ ਘਾਤੀ ਬਹੁਪਦ ਪ੍ਰਾਪਤ ਕਰਦੇ ਹਾਂ ।

ਪ੍ਰਸ਼ਨ (iii).
0, \(\sqrt {5}\)
ਉੱਤਰ:
ਦਿੱਤੇ ਗਏ ਸਿਫ਼ਰਾਂ ਦਾ ਜੋੜ ਅਤੇ ਗੁਣਨਫਲ ਕੁਮਵਾਰ 0 ਅਤੇ \(\sqrt {5}\) ਹੈ ।
ਮੰਨ ਲਉ ਕਿ ax² + bx + c ਇਕ ਦੋ ਘਾਤੀ ਬਹੁਪਦ ਹੈ α ਅਤੇ β ਸੁ ਇਸ ਦੇ ਸਿਫ਼ਰ ਹਨ ।
∴ α + β = ਸਿਫ਼ਰਾਂ ਦਾ ਜੋੜ = 0
ਅਤੇ αβ = ਸਿਫ਼ਰਾਂ ਦਾ ਗੁਣਨਫਲ = \(\sqrt {5}\)
ਹੁਣ, ax² + bx + c = k (x – α) (x – β)
ਜਿੱਥੇ k ਕੋਈ ਅਚਲ ਹੈ ।
= k [x² – (α + β)x + αβ)
= k[x² – 0x + \(\sqrt {5}\)]
= k[x² + \(\sqrt {5}\)]
k ਦੇ ਵੱਖ-ਵੱਖ ਮੁੱਲਾਂ ਦੇ ਲਈ ਅਸੀਂ ਵੱਖ-ਵੱਖ ਦੋ ਘਾਤੀ ਬਹੁਪਦ ਪ੍ਰਾਪਤ ਕਰਦੇ ਹਨ ।

ਪ੍ਰਸ਼ਨ (iv).
1, 1
ਉੱਤਰ:
ਦਿੱਤੇ ਗਏ ਸਿਫ਼ਰਾਂ ਦਾ ਜੋੜ ਅਤੇ ਗੁਣਨਫਲ ਕ੍ਰਮਵਾਰ 1 ਅਤੇ 1 ਹੈ ।
ਮੰਨ ਲਉ ਕਿ ax² + bx + c ਇਕ ਦੋ ਘਾਤੀ ਬਹੁਪਦ ਹੈ ਅਤੇ α ਅਤੇ β ਇਸ ਦੇ ਸਿਫ਼ਰ ਹਨ ।
∴ α + β = ਸਿਫ਼ਰਾਂ ਦਾ ਜੋੜ = 1
ਅਤੇ αβ = ਸਿਫ਼ਰਾਂ ਦਾ ਗੁਣਨਫਲ = 1
ਹੁਣ, ax² + bx + 0 = k (x – α) (x – β)
ਜਿੱਥੇ k ਕੋਈ ਅਚਰ ਹੈ ।
= k[x² – (α + β)x + αβ]
= k[x² – 1x + 1]
= k[x² – x + 1]
k ਦੇ ਵੱਖ-ਵੱਖ ਮੁੱਲਾਂ ਦੇ ਲਈ ਅਸੀਂ ਵੱਖ-ਵੱਖ ਬਹੁਪਦ | ਪ੍ਰਾਪਤ ਕਰਦੇ ਹਾਂ ।

ਪ੍ਰਸ਼ਨ (v).
\(-\frac{1}{4}\), \(\frac{1}{4}\)
ਉੱਤਰ:
ਦਿੱਤਾ ਗਿਆ ਹੈ ਕਿ ਬਹੁਪਦ ਦੀ ਸਿਫ਼ਰਾਂ ਦਾ ਜੋੜਫਲ ਅਤੇ ਗੁਣਨਫਲ ਕ੍ਰਮਵਾਰ \(\frac{-1}{4}\) ਅਤੇ \(\frac{1}{4}\) ਹੈ |
ਮੰਨ ਲਉ ਕਿ ax² + bx + c ਇਕ ਦੋ ਘਾਤੀ ਬਹੁਪਦ ਹੈ ਅਤੇ α ਅਤੇ β ਇਸਦੇ ਸਿਫ਼ਰ ਹਨ ।
∴ α + β = ਸਿਫ਼ਰਾਂ ਦਾ ਜੋੜ = \(\frac{-1}{4}\)
ਅਤੇ αβ = ਸਿਫ਼ਰਾਂ ਦਾ ਗੁਣਨਫਲ = \(\frac{1}{4}\)
ਹੁਣ, ax² + bx + c = k (x – α) (x – β)
ਜਿੱਥੇ ,k ਕੋਈ ਅਚਲ ਹੈ ।
= k[x² – (α + β)x + αβ]
= k[x² – \(\left(\frac{-1}{4}\right)\)x + \(\frac{1}{4}\)]
= k[x² + \(\frac{1}{4}\)x + \(\frac{1}{4}\)]
k ਦੇ ਵੱਖ-ਵੱਖ ਮੁੱਲਾਂ ਦੇ ਲਈ ਅਸੀਂ ਵੱਖ-ਵੱਖ ਬਹੁਪਦ ਪ੍ਰਾਪਤ ਕਰਦੇ ਹਾਂ ।

ਪ੍ਰਸ਼ਨ (vi).
4, 1
ਉੱਤਰ:
ਦਿੱਤਾ ਗਿਆ ਹੈ ਕਿ ਬਹੁਪਦ ਦੇ ਸਿਫ਼ਰਾਂ ਦਾ ਜੋੜ ਅਤੇ ਗੁਣਨਫਲ ਕ੍ਰਮਵਾਰ 4, ਅਤੇ 1 ਹੈ ।
ਮੰਨ ਲਉ ਕਿ ax² + bx + c ਇਕ ਦੋ ਘਾਤੀ ਬਹੁਪਦ ਹੈ ਅਤੇ α ਅਤੇ β ਇਸ ਦੀਆਂ ਸਿਫ਼ਰਾਂ ਹਨ ।
∴ α + β = ਸਿਫ਼ਰਾਂ ਦਾ ਜੋੜ = 4
ਅਤੇ αβ = ਸਿਫ਼ਰਾਂ ਦਾ ਗੁਣਨਫਲ = 1
ਹੁਣ, ax² + bx + c = k (x – α) (x – β)
ਜਿੱਥੇ k ਕੋਈ ਅਚਲ ਹੈ ।
= k [x² – (α + β)x + αβ)
= k[x² – 4x + 1]
k ਦੇ ਵੱਖ-ਵੱਖ ਮੁੱਲਾਂ ਲਈ ਅਸੀਂ ਵੱਖ-ਵੱਖ ਦੋ ਘਾਤੀ ਬਹੁਪਦ ਪ੍ਰਾਪਤ ਕਰਦੇ ਹਾਂ ।