PSEB 10th Class Maths Solutions Chapter 2 ਬਹੁਪਦ Ex 2.3

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 2 ਬਹੁਪਦ Ex 2.3 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 10 Maths Chapter 2 ਬਹੁਪਦ Exercise 2.3

1. ਵੰਡ ਐਲਗੋਰਿਥਮ ਦੀ ਵਰਤੋਂ ਕਰਕੇ, ਹੇਠਾਂ ਦਿੱਤਿਆਂ ਵਿੱਚ ਬਹੁਪਦ p(x) ਨੂੰ ਬਹੁਪਦ g(x) ਨਾਲ ਭਾਗ ਕਰਕੇ ਭਾਗਫਲ ਅਤੇ ਬਾਕੀ ਪਤਾ ਕਰੋ :

ਪ੍ਰਸ਼ਨ (i).
p(x) = x³ – 3x² + 5x – 3, g(x) = x² – 2
ਉੱਤਰ:
ਦਿੱਤਾ ਹੈ p(x) = x³ – 3x² + 5x – 3
ਅਤੇ g(x) = x² – 2

ਵੰਡ ਐਲਗੋਰਿਥਮ ਤੋਂ,
x³ – 3x² + 5x – 3
= (x – 3) (x² – 2) + (7x – 9)
ਭਾਗਫਲ = x – 3, ਬਾਕੀ = 7x – 9

ਪ੍ਰਸ਼ਨ (ii).
p(x) = x⁴ – 3x² + 4x + 5, g(x) = x² + 1 – x
ਉੱਤਰ:
ਦਿੱਤਾ ਹੈ p(x) = x⁴ – 3x² + 4x + 5
ਜਾਂ p(x) = x⁴ + 0x³ – 3x² + 4x + 5
ਅਤੇ g(x) = x² + 1 – x
ਜਾਂ g(x) = x² – x + 1

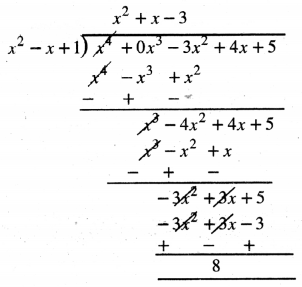
ਵੰਡ ਐਲਗੋਰਿਥਮ ਤੋਂ, ਮਾਂ
x⁴ – 3x² + 4x + 5
= (x² + x – 3) (x² – x + 1) + 8
ਭਾਗਫਲੇ = x² + x – 3
ਅਤੇ ਬਾਕੀ = 8

ਪ੍ਰਸ਼ਨ (iii).
p(x) = x⁴ – 5x + 6, g(x) = 2 – x²
ਉੱਤਰ:
ਦਿੱਤਾ ਹੈ p(x) = x⁴ – 5x + 6
ਜਾਂ p(x) = x⁴ + 0³ + 0x² – 5x + 6
ਅਤੇ g(x) = 2 – x²
ਜਾਂ g(x) = -x² + 2

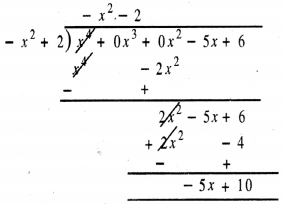
ਵੰਡ ਐਲਗੋਰਿਥਮ ਤੋਂ,
x⁴ – 5x + 6
= (-x² – 2) (-x² + 2) + (-5x + 10)
ਇਸ ਲਈ, ਭਾਗਫਲ = -x² – 2,
ਬਾਕੀ = – 5x + 10

2. ਦੂਸਰੀ ਬਹੁਪਦ ਨੂੰ ਪਹਿਲੀ ਬਹੁਪਦ ਨਾਲ ਭਾਗ ਕਰਕੇ ਪਤਾ ਕਰੋ ਕਿ ਕੀ ਪਹਿਲੀ ਬਹੁਪਦ, ਦੂਸਰੀ ਬਹੁਪਦ ਦਾ ਗੁਣਨਖੰਡ ਹੈ ।

ਪ੍ਰਸ਼ਨ (i).
t² – 3, 2t⁴ + 3t³ – 2t² – 9t – 12
ਉੱਤਰ:

∵ ਬਾਕੀ ਸਿਫ਼ਰ ਹੈ ।
∴ ਵੰਡ ਐਲਗੋਰਿਥਮ ਤੋਂ
t² – 3, 2t⁴ + 3t³ – 2t² – 9t – 12 ਦਾ ਗੁਣਨਖੰਡ ਹੈ ।

ਪ੍ਰਸ਼ਨ (ii).
x² + 3x + 1, 3x⁴ + 5x³ – 7x² + 2x + 2
ਉੱਤਰ:

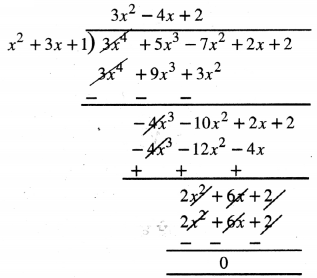
∵ ਬਾਕੀ ਸਿਫ਼ਰ ਹੈ ।
∴ ਵੰਡ ਐਲਗੋਰਿਥਮ ਤੋਂ
x² + 3x + 1, 3x⁴ + 5x³ – 7x² + 2x + 2 ਦਾ ਗੁਣਨਖੰਡ ਹੈ ।

ਪ੍ਰਸ਼ਨ (iii).
x³ – 3x + 1, x⁵ – 4x³ + x² + 3x + 1
ਉੱਤਰ:

∵ ਬਾਕੀ ਸਿਫ਼ਰ ਨਹੀਂ ਹੈ
∴ ਵੰਡ ਐਲਗੋਰਿਥਮ x³ – 3x + 1,
x⁵ – 4x³ + x² + 3x + 1 ਦਾ ਗੁਣਨਖੰਡ ਨਹੀਂ ਹੈ ।

ਪ੍ਰਸ਼ਨ 3.
ਜੇਕਰ 3x⁴ + 6x³ – 2x² – 10x – 5, ਦੇ ਦੋ ਸਿਫ਼ਰ \(\sqrt{\frac{5}{3}}\) ਅਤੇ \(-\sqrt{\frac{5}{3}}\) ਹੋਣ ਤਾਂ ਬਾਕੀ ਦੀਆਂ ਸਿਫਰਾਂ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਦਿੱਤੀਆਂ ਗਈਆਂ ਦੋ ਸਿਫ਼ਰਾਂ \(\sqrt{\frac{5}{3}}\) ਅਤੇ \(-\sqrt{\frac{5}{3}}\)
∴ (x – \(\sqrt{\frac{5}{3}}\))[x – (-\(\sqrt{\frac{5}{3}}\))] ਦਿੱਤੇ ਹੋਏ ਬਹੁਪਦ ਦਾ ਇੱਕ ਗੁਣਨਖੰਡ ਹੈ ।
ਜਾਂ (x – \(\sqrt{\frac{5}{3}}\))(x + \(\sqrt{\frac{5}{3}}\)) ਦਿੱਤੇ ਗਏ ਬਹੁਪਦ ਦਾ ਇੱਕ ਗੁਣਨਖੰਡ ਹੈ ।
ਜਾਂ x² – \(\frac{5}{3}\) ਦਿੱਤੇ ਗਏ ਬਹੁਪਦ ਦਾ ਇੱਕ ਗੁਣਨਖੰਡ ਹੈ ।
ਇਸ ਲਈ, ਦਿੱਤੇ ਗਏ ਬਹੁਪਦ ਅਤੇ x² – \(\frac{5}{3}\) ਵੰਡ ਐਲਗੋਰਿਥਮ ਦਾ ਪ੍ਰਯੋਗ ਕਰਦੇ ਹੋਏ,

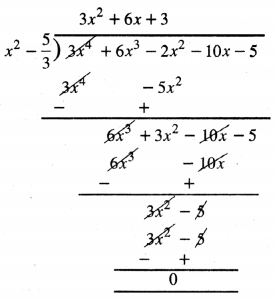
∴ 3x² + 6x³ + 2x² – 10x – 5
= (x² – \(\frac{5}{3}\))[3x² + 6x + 3] S = 2, P = 1
= (x² – \(\frac{5}{3}\))(3)[x² + 2x + 1]
= 3(x² – \(\frac{5}{3}\))[x² + x + x + 1]
= 3(x² – \(\frac{5}{3}\))[x(x + 1) + 1(x + 1)]
= 3(x² – \(\frac{5}{3}\))(x + 1)(x + 1)
ਹੁਣ, ਬਹੁਪਦ ਦੇ ਬਾਕੀ ਸਿਫ਼ਰ ਦਿੱਤੇ ਗਏ
x + 1 = 0 ਜਾਂ x + 1 = 0
x = – 1 ਜਾਂ x = – 1
∴ ਦਿੱਤੇ ਗਈ ਚਾਰ ਘਾਤ ਵਾਲੀ ਬਹੁਪਦ ਦੇ ਸਿਫ਼ਰ ਹਨ :
\(\sqrt{\frac{5}{3}}\), \(-\sqrt{\frac{5}{3}}\), -1, -1

ਪ੍ਰਸ਼ਨ 4.
ਬਹੁਪਦ x³ – 3x² + x + 2 ਨੂੰ ਬਹੁਪਦ g(x) ਨਾਲ ‘ ਭਾਗ ਦੇਣ ‘ ਤੇ ਭਾਗਫਲ x – 2 ਅਤੇ ਬਾਕੀ -2x + 4 ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਤਾਂ g(x) ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਮੰਨ ਲਓ
p (x) = x³ – 3x² + x + 2
ਅਤੇ q(x) = (x – 2)
ਅਤੇ r(x) = – 2x + 4
ਦਿੱਤੇ ਗਏ ਅੰਕੜਿਆਂ ਦੀ ਵੰਡ ਐਲਗੋਰਿਥਮ ਨਾਲ ਤੁਲਨਾ ਕਰਨ ਤੇ
p(x) = g(x). q(4) + r(x)
ਜਾਂ p(x) – r(x) = g(x) . q (x)
ਜਾਂ g(x) . q(x) = p(x) – r(x)
ਜਾਂ g(x) = \(\frac{p(x)-r(x)}{q(x)}\)
ਅਲਗ-ਅਲਗ ਮੁੱਲ ਰੱਖਣ ਤੇ ਅਸੀਂ ਪ੍ਰਾਪਤ ਕਰਦੇ

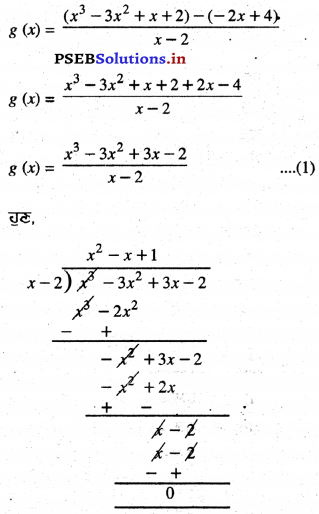
∴ \(\frac{x^{3}-3 x^{2}+3 x-2}{x-2}\) = x² – x + 1 ….(2)
(1) ਅਤੇ (2), ਤੋਂ ਸਾਨੂੰ ਮਿਲਦਾ ਹੈ :
g(x) = x² – x + 1

5. ਬਹੁਪਦ p (x), g (x), q (x) ਅਤੇ r (x) ਦੇ ਅਜਿਹੇ ਉਦਾਹਰਣਾਂ ਦਿਉ ਜੋ ਵੰਡ ਐਲਗੋਰਿਥਮ ਨੂੰ ਸੰਤੁਸ਼ਟ ਕਰਦੇ ਹੋਣ ਅਤੇ

ਪ੍ਰਸ਼ਨ (i).
ਘਾਤ p (x) = ਘਾਤ q (x)
ਉੱਤਰ:
p(x) = x² – 5x + 10, g(x) = 5
q(x) = x² – x + 2; r(x) = 0

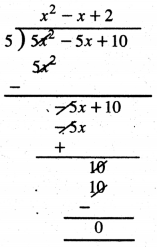
∴ ਵੰਡ ਐਲਗੋਰਿਥਮ ਤੋਂ
5x² – 5x + 10 = 5 (x² – x + 2) + 0
ਜਾਂ p(x) = g(x) q(x) + r(x)
ਨਾਲ ਹੀ, p (x) ਦੀ ਘਾਤ = q (x) ਦੀ ਘਾਤ = 2

ਪ੍ਰਸ਼ਨ (ii).
ਘਾਤ q (x) = ਘਾਤ r (x)
ਉੱਤਰ:
ਮੰਨ ਲਓ p (x) = 7x³ – 42x + 53;
g(x) = x³ – 6x + 7;
q(x) = 7; r(x) = 4

∴ ਵੰਡ ਐਲਗੋਰਿਥਮ ਤੋਂ
7x³ – 42x + 53
= 7(x³ – 6x + 7) + 4
ਜਾਂ p(x) = q (1) g (x) + r (x)
ਨਾਲ ਹੀ, ਘਾਤ q (x) = 0.

ਪ੍ਰਸ਼ਨ (iii).
ਘਾਤ r (x) = 0
ਉੱਤਰ:
ਮੰਨ ਲਓ p (x) = 4x³ + x² + 3x + 6;
g(x) = x² + 3x + 1;
q(x) = 4x – 11; r(x) = 32x + 17

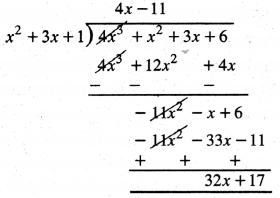
∴ ਵੰਡ ਐਲਗੋਰਿਥਮ ਤੋਂ
4x³ + x² + 3x + 6
= (4x – 11) (x² + 3x + 1) + (32x + 17)
ਜਾਂ p(x) = q(x)∙g(x) + r(x)
ਨਾਲ ਹੀ, ਘਾਤ q(x) = ਘਾਤ r(x)