PSEB 10th Class Maths Solutions Chapter 2 ਬਹੁਪਦ Ex 2.4

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 2 ਬਹੁਪਦ Ex 2.4 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 10 Maths Chapter 2 ਬਹੁਪਦ Exercise 2.4

1. ਸਿੱਧ ਕਰੋ ਕਿ ਹੇਠਾਂ ਦਿੱਤੀ ਤਿੰਨ ਘਾਤੀ ਬਹੁਪਦਾਂ ਦੇ ਨਾਲ ਦਿੱਤੀਆਂ ਸੰਖਿਆਵਾਂ ਉਹਨਾਂ ਦੀਆਂ ਸਿਫ਼ਰਾਂ ਹਨ । ਹਰ ਇੱਕ ਸਥਿਤੀ ਵਿਚ ਸਿਫ਼ਰਾਂ ਅਤੇ ਗੁਣਾਂਕਾਂ ਵਿਚਕਾਰ ਸੰਬੰਧਾਂ ਦੀ ਵੀ ਜਾਂਚ ਕਰੋ :

ਪ੍ਰਸ਼ਨ (i).
2x³ + x² – 5x + 2; \(\frac{1}{2}\), 1, – 2
ਉੱਤਰ:
ਮੰਨ ਲਉ p (x) = 2x³ + x² – 3x + 2
ਇਸ ਦੀ ਤੁਲਣਾ ax² + bx² + cx + d ਨਾਲ ਕਰਨ ‘ਤੇ
∴ a = 2, b = 1, c = – 5, d = 2

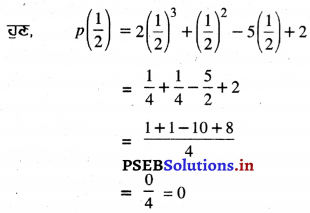
∴ \(\frac{1}{2}\), p(x) ਦਾ ਇੱਕ ਸਿਫ਼ਰ ਹੈ ।
ਅਤੇ p(1) = 2(1)³ + (1)² – 5(1) + 2
= 2 + 1 – 5 + 2 = 5 – 5 = 0
∴ 1, p (1) ਦਾ ਇੱਕ ਸਿਫ਼ਰ ਹੈ ।
ਨਾਲ ਹੀ, p(-2) = 2(-2)³ + (-2)² – 5(-2) + 2
= – 16 +4 + 10 + 2
= – 16 + 16 = 0
∴ – 2, p (x) ਦਾ ਇੱਕ ਸਿਫ਼ਰ ਹੈ ।
ਉਪਰੋਕਤ ਤੋਂ ਇਹ ਸਪੱਸ਼ਟ ਹੈ ਕਿ \(\frac{1}{2}\), 1, – 2 ਦਿੱਤੇ ਗਏ ਬਹੁਪਦ ਦੇ ਸਿਫ਼ਰ ਹਨ ।
ਮੰਨ ਲਉ ਕਿ ਇਹ ਸਿਫ਼ਰ ਹਨ :
α = \(\frac{1}{2}\), β = 1, γ = -2
ਹੁਣ, α + β + γ = \(\frac{1}{2}\) + 1 + (-2)
= \(\frac{1}{2}\) + 1 – 2 = \(\frac{1+2-4}{2}\)
= \(\frac{-1}{2}\)
= \(\frac{-a}{b}\)
αβ + βγ + γα = \(\left(\frac{1}{2}\right)\)(1) + (-1)(-2) + (-2)\(\left(\frac{1}{2}\right)\)
= \(\frac{1}{2}\) – 2 – 1 = \(\frac{1-4-2}{2}\)
= \(\frac{-5}{2}\) = \(\frac{c}{a}\)
αβγ = \(\left(\frac{1}{2}\right)\)(1)(-2) = \(\frac{-2}{2}\) = \(\frac{-d}{a}\)
ਉਪਰੋਕਤ ਤੋਂ ਇਹ ਸਪੱਸ਼ਟ ਹੈ ਕਿ ਸਿਫ਼ਰਾਂ ਅਤੇ ਗੁਣਾਂਕਾਂ ਵਿਚ ਸੰਬੰਧ ਹੈ ।

ਪ੍ਰਸ਼ਨ (ii).
x³ – 4x² + 5x – 2; 2, 1, 1
ਉੱਤਰ:
ਮੰਨ ਲਉ p(x) = x³ – 4x² + 5x – 2.
ਇਸਦੀ ਤੁਲਣਾਂ ax³ + bx² + cx + d ਨਾਲ ਕਰਨ ਤੇ
∴ a = 1, b = – 4, c = 5, d = – 2
ਹੁਣ p (2) = (2)³ – 4(2)² + 5(2) – 2
= 8 – 16 + 10 – 2
= 18 – 18
= 0
∴ 2, p (2) ਦਾ ਇੱਕ ਸਿਫ਼ਰ ਹੈ ।
ਅਤੇ p (1) = (1)³ – 4(1)³ + 5(1) – 2
= 1 – 4 + 5 – 2
= 6 – 6 = 0
∴ 1, p (1) ਦਾ ਇੱਕ ਸਿਫ਼ਰ ਹੈ ।
ਉਪਰੋਕਤ ਤੋਂ ਇਹ ਸਪੱਸ਼ਟ ਹੈ ਕਿ 2, 1, 1 ਦਿੱਤੇ ਗਏ | ਬਹੁਪਦ ਦੇ ਸਿਫ਼ਰ ਹਨ ।
ਮੰਨ ਲਉ ਇਹ ਸਿਫ਼ਰ ਹਨ ।
α = 2, β = 1, γ = 1
ਹੁਣ, α + β + γ = 2 + 1 + 1 = 4
= \(\frac{-(-4)}{1}\) = \(\frac{-b}{a}\)
αβ + βγ + γα = (2)(1) + (1)(1) + (1)(2)
= 2 + 1 + 2 = 5
= \(\frac{5}{1}\) = \(\frac{c}{a}\)
αβγ = (2)(1)(1) = 2
= \(\frac{-(-2)}{1}\) = \(\frac{-d}{a}\)
ਉਪਰੋਕਤ ਤੋਂ ਇਹ ਸਪੱਸ਼ਟ ਹੈ ਕਿ ਸਿਫ਼ਰਾਂ ਅਤੇ ਗੁਣਾਂਕਾਂ ਵਿਚ ਸੰਬੰਧ ਹੈ ।

ਪ੍ਰਸ਼ਨ 2.
ਇਕ ਤਿੰਨ ਘਾਤੀ ਬਹੁਪਦ ਪਤਾ ਕਰੋ ਜਿਸ ਦੀਆਂ ਸਿਫ਼ਰਾਂ ਦਾ ਜੋੜ, ਦੋ ਸਿਫ਼ਰਾਂ ਨੂੰ ਇਕੱਠਾ ਲੈ ਕੇ ਉਹਨਾਂ ਦੇ ਗੁਣਨਫਲਾਂ ਦਾ ਜੋੜ ਅਤੇ ਤਿੰਨਾਂ ਸਿਫ਼ਰਾਂ ਦਾ ਗੁਣਨਫਲ ਕੁਮਵਾਰ 2, – 7, – 14 ਹੈ ।
ਹੱਲ:
ਤਿੰਨ ਘਾਤੀ ਬਹੁਪਦ ਦਾ ਸਰਬਵਿਆਪਕ ਵਿਅੰਜਕ ਹੈ ।
ax³ + bx² + cx + d.
ਮੰਨ ਲਉ , α, β, γ ਇਸ ਦੇ ਸਿਫ਼ਰ ਹਨ ।
∴ α + β + γ = ਸਿਫ਼ਰਾਂ ਦਾ ਜੋੜ = 2
αβ + βγ + γα = ਸਿਫ਼ਰਾਂ ਦੇ ਗੁਣਨਫਲਾਂ ਦਾ ਜੋੜ = – 7
αβγ = ਸਿਫ਼ਰਾਂ ਦਾ ਗੁਣਨਫਲ = – 14
∴ ax² + bx² + cx + d
= k [(x – α) (x – β) (x – γ)] ਜਿੱਥੇ k ਕੋਈ ਅਚਲ ਹੈ ।
= k [x³ – (α + β + γ)x² + (αβ + βγ + γα)x – αβγ]
= k [x³ – 2x² – 7x + 14] [(1) ਦਾ ਪ੍ਰਯੋਗ ਕਰਕੇ]
k, ਦੇ ਅਲੱਗ-ਅਲੱਗ ਮੁੱਲਾਂ ਲਈ ਅਸੀਂ ਅਲੱਗ-ਅਲੱਗ ਤਿੰਨ ਘਾਤੀ ਪ੍ਰਾਪਤ ਕਰਦੇ ਹਾਂ ।

ਪ੍ਰਸ਼ਨ 3.
ਜੇਕਰ ਬਹੁਪਦ x³ – 3x² + x + 1 ਦੀਆਂ ਸਿਫਰਾਂ a – b, a, a + b, ਹੋਣ ਤਾਂ a ਅਤੇ b ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਮੰਨ ਲਉ p (x) = x³ – 3x² + x + 1
ਇਸਦੇ ਸਿਫ਼ਰ a – b, a, a + b ਹਨ
a – b, p (x) ਦਾ ਸਿਫ਼ਰ ਹੈ । …(ਦਿੱਤਾ ਹੈ।)
p (a – b) = 0
ਜਾਂ (a – b)³ – 3(a – b)² + (a – b) + 1 = 0
ਜਾਂ [a³– b³ – 3a²b + 3ab²] – 3 [a² + b² – 2ab] + a – b + 1 = 0
ਜਾਂ a³ – b³ – 3a²b + 3ab² – 3a² – 3b² + 6ab + a – b + 1 = 0 ….(1)
ਅਤੇ a, p (x) ਦਾ ਸਿਫ਼ਰ ਹੈ ….(ਦਿੱਤਾ ਹੈ।)
∴ p (a) = 0
ਜਾਂ a³ – 3a³ + a + 1 = 0 …(2)
ਨਾਲ ਹੀ, a + b, p (x) ਦਾ ਸਿਫ਼ਰ ਹੈ ..(ਦਿੱਤਾ ਹੈ।)
∴ p (a + b) = 0
ਜਾਂ (a + b)³ – 3 (a + b)² + (a + b) + 1 = 0
ਜਾਂ (a³ + b³ + 3a²b + 3ab²) – 3 (a² + b² + 2ab) + a + b – 1 = 0
ਜਾਂ a³ + b³ + 3a²b + 3ab² – 3a² – 3b² – 6ab + a + b + 1 = 0 ….(3)
(1) ਅਤੇ (3), ਨੂੰ ਜੋੜ ਕੇ ਅਸੀਂ ਪ੍ਰਾਪਤ ਕਰਦੇ ਹਾਂ
2a³ + 6ab² – 6a² – 6b² + 2 + 2 = 0
ਜਾਂ a³ + 3ab² – 3a² – 3b² + a + 1 = 0
ਜਾਂ (a³ – b³ + 4 + 1) + (3ab² – 3b²) = 0
ਜਾਂ 0 + 3b²(a – 1) – 0[(2) ਦਾ ਪ੍ਰਯੋਗ ਕਰਨ ਤੇ]
ਜਾਂ a – 1 = 0
ਜਾਂ a = 1 …(4)
(3) ਅਤੇ (4), ਤੋਂ ਅਸੀਂ ਪ੍ਰਾਪਤ ਕਰਦੇ ਹਾਂ ।
(1)³ + b³ + 3(1)²b + 3(1)b² – 3 (1)² – 3b² – 6 (1) b + 1 + b + 1 = 0
ਜਾਂ 1+ b³ + 3b + 3b² – 3 – 3b² – 6b + b + 2 = 0
ਜਾਂ b³ – 2b = 0 ਜਾਂ b (b² – 2) = 0
ਜਾਂ b² – 2 = 0 ਜਾਂ b² = 2
ਜਾਂ b = ±\(\sqrt {2}\)
ਇਸ ਲਈ, a = 1, b = ±\(\sqrt {2}\)
ਵੈਕਲਪਿਕ ਹੱਲ
ਦਿੱਤਾ ਹੈ ਕਿ ਕਿ ਬਹੁਪਦ x³ – 3x² + x + 1 ਦੇ ਤਿੰਨ ਸਿਫ਼ਰ ਕ੍ਰਮਵਾਰ a – b, a, a + b ਹਨ ।
ਹੁਣ, ਸਿਫ਼ਰਾਂ ਦਾ ਜੋੜਫਲ = (a – b) + a + (a + b)
= a – b + a + a + b
= 3a,
ਪਰੰਤੂ ਗੁਣਾਂਕਾਂ ਦਾ ਪ੍ਰਯੋਗ ਕਰਕੇ ਸਿਫ਼ਰਾਂ ਦਾ ਜੋੜਫਲ

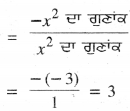
∴ 3a = 3 ਜਾਂ a = 1
ਨਾਲ ਹੀ, ਸਿਫ਼ਰਾਂ ਦਾ ਗੁਣਨਫਲ = (a – b) . a . (a + b)
= (a² – b²) a
a ਦਾ ਮੁੱਲ ਭਰਨ ਤੇ ਅਸੀਂ ਪ੍ਰਾਪਤ ਕਰਦੇ ਹਾਂ :
= (1² – b²) . 1
= (1 – b²)
ਪਰੰਤੂ ਗੁਣਾਂਕਾਂ ਦਾ ਪ੍ਰਯੋਗ ਕਰਕੇ ਸਿਫਰਾਂ ਦਾ ਗੁਣਨਫਲ

∴ 1 – b² = – 1
-b² = -1 – 1
-b² = – 2 ਜਾਂ b² = 2
b = ±\(\sqrt {2}\)
ਇਸ ਲਈ a = 1 ਅਤੇ b = ±\(\sqrt {2}\)

ਪ੍ਰਸ਼ਨ 4.
ਜੇਕਰ ਬਹੁਪਦ x⁴ – 6x³ – 26x² + 138x – 35 ਦੇ ਦੋ ਸਿਫ਼ਰ 2 ± \(\sqrt {3}\) ਹੋਣ, ਤਾਂ ਬਾਕੀ ਦੀਆਂ ਸਿਫ਼ਰਾਂ ਪਤਾ ਕਰੋ :
ਹੱਲ:
ਦਿੱਤੇ ਹੋਏ ਦੋ ਸਿਫ਼ਰਾਂ (2 + \(\sqrt {3}\)) ਅਤੇ (2 – \(\sqrt {3}\)) ਹਨ ।

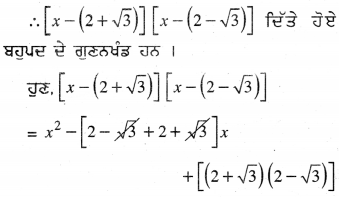
= x² – 4x + [(2)² – (\(\sqrt {3}\))²]
= x² – 4x + 1
∴ (x² – 4x + 1) ਬਹੁਪਦ ਦਾ ਗੁਣਨਖੰਡ ਹੈ । ਹੁਣ ਦਿੱਤੇ ਗਏ ਬਹੁਪਦ ਅਤੇ (x² – 4x + 1) ਉੱਤੇ ਵੰਡ ਐਲਗੋਰਿਥਮ ਦਾ ਪ੍ਰਯੋਗ ਕਰਨ ਤੇ

∴ x⁴ – 6x³ – 26x² + 138x – 35
= (x² – 4x + 1) (x² – 2x – 35)
= (x² – 4x + 1) [x² + 5x – 7x – 35) | S = – 2, P = – 35
= (x² – 4x + 1) [(x + 5) – 7(x + 5)]
= (x² – 4x + 1) (x + 5) (x – 7)
ਹੁਣ, ਬਹੁਪਦ ਦੇ ਬਾਕੀ ਸਿਫ਼ਰ ਹਨ
x + 5 = 0 ਜਾਂ x – 7 = 0
x = – 5 ਜਾਂ x = 7
∴ ਦਿੱਤੀ ਗਈ ਚਾਰ ਘਾਤ ਵਾਲੀ ਬਹੁਪਦ ਦੇ ਸਿਰ ਹਨ :
2 + \(\sqrt {3}\), 2 – \(\sqrt {3}\), – 5, 7

ਪ੍ਰਸ਼ਨ 5.
ਜੇਕਰ ਬਹੁਪਦ x⁴ – 6x³ + 16x² – 25x + 10 ਨੂੰ ਦੂਸਰੇ ਬਹੁਪਦ x² – 2x + k ਨਾਲ ਭਾਗ ਕੀਤਾ ਜਾਵੇ ਅਤੇ ਬਾਕੀ x + a, ਪ੍ਰਾਪਤ ਹੋਵੇ ਤਾਂ k ਅਤੇ a ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਦਿੱਤਾ ਗਿਆ ਹੈ ਕਿ ਬਹੁਪਦ x⁴ – 6x³ + 16x² – 25x + 10 ਨੂੰ ਇਕ ਦੂਸਰੇ ਬਹੁਪਦ x² – 2x + k ਨਾਲ | ਭਾਗ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ਤਾਂ ਬਾਕੀ x + a ਆਉਂਦਾ ਹੈ ।
ਇਸ ਲਈ ਸਭ ਤੋਂ ਪਹਿਲਾਂ
x⁴ – 6x³ + 16x² – 25x + 10 ਨੂੰ x² – 2x + k ਨਾਲ ਭਾਗ ਕਰਦੇ ਹਾਂ ਅਤੇ ਬਾਕੀ ਅਤੇ ਭਾਗਫਲ ਪਤਾ ਕਰਦੇ ਹਾਂ

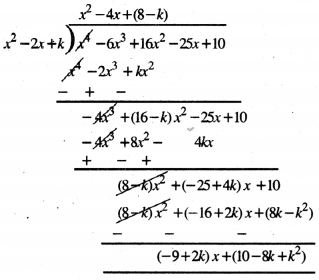
∴ ਬਹੁਪਦ x⁴ – 6x³ + 16x² – 25x + 10
ਦੇ ਵੰਡ ਐਲਗੋਰਿਥਮ ਤੋਂ
= (x² – 2x + k) [x² – 4x + (8 – k)] + [(-9 + 2k) + (10 – 8k + k²]
∴ ਭਾਗਫਲ = x² – 4x + (8 – k)
ਅਤੇ ਬਾਕੀ = (-9 + 2k) x + (10 – 8k + k²)
ਪਰੰਤੂ ਬਾਕੀ = x + a ….(ਦਿੱਤਾ ਹੈ।)
∴ (-9 +2k)x + (10 – 8k + k²)
= x + a
ਗੁਣਾਂ ਦੀ ਤੁਲਣਾ ਕਰਨ ਤੇ
-9 + 2k = 1 ਜਾਂ 10 – 8k + k² = a
2k = 1 + 9
2k = 10, ਅਸੀਂ ਦੇਖਦੇ ਹਾਂ
k = \(\frac{10}{2}\) = 5
ਹੁਣ, 10 – 8k + k² = a
k ਦਾ ਮੁੱਲ ਰੱਖਣ ਤੇ ਪ੍ਰਾਪਤ ਕਰਦੇ ਹਾਂ
10 – 8 × 5 + (5)² = a
10 – 40 + 25 = a
k = 5
-5 = a
a = – 5
ਇਸ ਲਈ, k = 5 ਅਤੇ a = – 5