Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 3 दो चर वाले रैखिक समीकरण युग्म Ex 3.1 Textbook Exercise Questions and Answers
PSEB Solutions for Class 10 Maths Chapter 3 दो चर वाले रैखिक समीकरण युग्म Ex 3.1
प्रश्न 1.
आफ़ताब अपनी पुत्री से कहता है, ‘सात वर्ष पूर्व मैं तुमसे सात गुनी आयु का था। अब से 3 वर्ष बाद मैं तुमसे केवल तीन गुनी आयु का रह जाऊँगा।’ (क्या यह मनोरंजक है ?) इस स्थिति को बीजगणितीय एवं ग्राफीय रूपों में व्यक्त कीजिए।
हल :
मान लीजिए आफ़ताब की वर्तमान आयु है = x वर्ष
और आफ़ताब की पुत्री की वर्तमान आयु = y वर्ष
बीज गणितीय स्थिति
प्रश्न की पहली शर्त के अनुसार,
x – 7 = 7 (y – 7) .
या x – 7 = 7y – 49
या x – 7y + 42 = 0
प्रश्न की दूसरी शर्त के अनुसार,
x + 3 = 3 (y + 3)
या x + 3 = 3y + 9
या x-3y – 6 = 0
∴ दो चरो में रैखिक समीकरण युग्म हैं :
x – 7y + 42 = 0
तथा x – 3y – 6 = 0.
आलेखीय स्थिति में
x – 7y + 42 = 0
x = 7y – 42 ……………(1)
y = 5. को (1) में प्रतिस्थापित करने पर, हमें प्राप्त होता है:
x = 7 × 5 – 42
= 35 – 42
= – 7
y = 6 को (1) में प्रतिस्थापित करने पर हमें प्राप्त होता है:
x = 7 × 6 – 42
= 42 – 42 = 0
y = 7 को (1) में प्रतिस्थापित करने पर हमें प्राप्त होता है:
x = 7 × 7 – 42
= 49 – 42 = 7
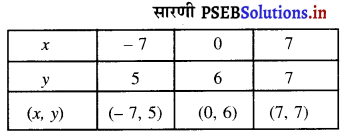
बिंदुओं A (- 7, 5), B (0, 6), C (7, 7) को आलेखित करने और उन्हें मिलाते हुए रेखा खींचने पर हमें समीकरण x – 7y + 42 = 0 का आलेख प्राप्त होता है।
x – 3y – 6 = 0
x = 3y + 6 ……………(2)
y = 0 को (2), में प्रतिस्थापित करने पर हमें प्राप्त होता है:
x = 3 × 0 + 6
= 0 + 6 = 6
y = 3 को (2) में प्रतिस्थापित करने पर, हमें प्राप्त होता है:
x = 3 × 3 + 6
= 9 + 6 = 15
y = – 2 को (2) में प्रतिस्थापित करने पर, हमें प्राप्त होता है:
x = 3 × – 2 + 6
= – 6 + 6 = 0
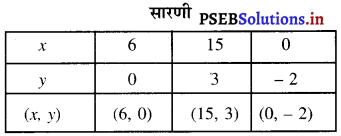
बिंदुओं D (6, 0), E (15, 3), F (0, – 2) आलेखित करने और उन्हें मिलाते हुए रेखा खींचने पर हमें समीकरण x – 3y – 6 = 0 का आलेख प्राप्त होता है।

आलेख से यह स्पष्ट है कि दोनों रेखाएँ G (42, 12) पर प्रतिच्छेद करती हैं।
अत: x = 42 और y = 12 समीकरण-युग्म का हल है।
![]()
प्रश्न 2.
क्रिकट टीम के एक कोच ने ₹ 3900 में 3 बल्ले और 6 गेदें खरीदी। बाद में उसने एक और बल्ला तथा उसी प्रकार की 3 गेदें ₹ 1300 में खरीदी। इस स्थिति को बीजगणितीय तथा ज्यामितिय रूपों में व्यक्त कीजिए।
हल :
मान लीजिए एक बल्ले का मूल्य = ₹ x
एक गेंद का मूल्य = ₹ y
बीज गणितीय हल
प्रश्न की पहली शर्त अनुसार,
3x + 6y = 3900
⇒ x + 2y = 1300
प्रश्न की दूसरी शर्त अनुसार,
1x + 3y = 1300
∴ दो चरों में रैखिक समीकरण-युग्म हैं
x + 2y = 1300
और x + 3y = 1300, उत्तर
आलेखीय स्थिति में
x + 2y = 1300
x = 1300 – 2 ………………(1)
y = 0 को (1) में प्रतिस्थापित करने पर हमें प्राप्त होता है :
x = 1300 – 2 × 0
x = 1300
y = 500 को (1) में प्रतिस्थापित करने पर हमें प्राप्त होता है :
x = 1300 – 2 × 500
= 1300 – 1000 = 300
y = 650 को (1) में प्रतिस्थापित करने पर हमें प्राप्त होता है :
x = 1300 – 2 × 650
= 1300 – 1300 = 0
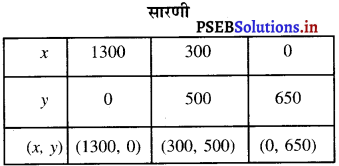
बिंदुओं A (1300, 0), B (300, 500) और C (0, 650) को आलेखित करने और उन्हें मिलाते हुए
रेखा खींचने पर हमें समीकरण x + 2 = 1300 का आलेख प्राप्त होता है
अब, x + 3y = 1300
x = 1300 – 3y …………..(2)
y = 0 को (2) में प्रतिस्थापित करने पर हमें प्राप्त होता है :
x = 1300 – 3 × 0
= 1300
y = 500 को (2) में प्रतिस्थापित करने पर हमें प्राप्त होता है :
x = 1300 – 3 × 500
= 1300 – 1500 = – 200
y = 300 को (2) में प्रतिस्थापित करने पर हमें प्राप्त होता है :
x = 1300 – 3 × 300
= 1300 – 900 = 400
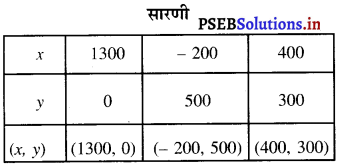
बिंदुओं A (1300, 0), E (- 200, 500), F (400, 300) को आलेखित करने और उन्हें मिलाते हुए रेखा खींचने पर हमें समीकरण x + 3y = 1300 का आलेख प्राप्त होता है।
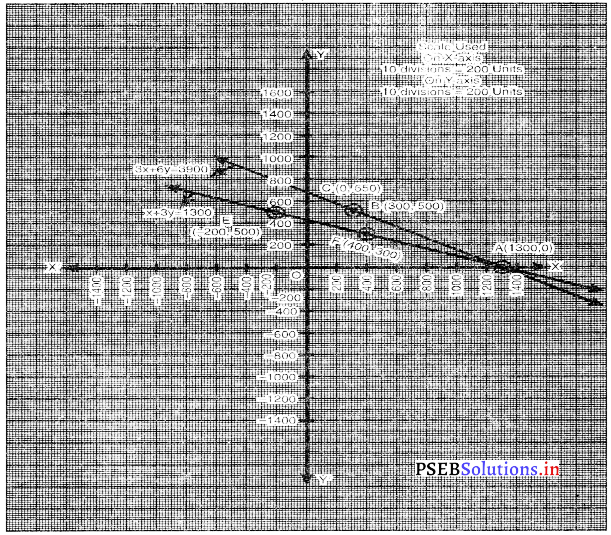
आलेख से यह स्पष्ट हैकि दोनों रेखाएँA (1300, 0) पर प्रतिच्छेद करती हैं।
अतः, x = 1300 और y = 0 दिए गए रैखिक समीकरण-युग्म का हल है।
![]()
प्रश्न 3.
2 kg सेब और 1 kg अंगूर का मूल्य किसी दिन ₹ 160 था। एक महीने बाद 4 kg सेब औ दो kg अंगूर का मूल्य ₹ 300 हो जाता है। इस स्थिति को बीजगणितीय तथा ज्यामितीय रूपों में व्यक्त कीजिए।
हल :
मान लीजिए 1 कि.ग्रा. सेबों का मूल्य = ₹ x
1 कि.ग्रा. अंगूर का मूल्य = ₹y
बीज गणितीय स्थिती में,
प्रश्न की पहली शर्त अनुसार,
2x + 1y = 160
प्रश्न की दूसरी शर्त अनुसार,
4x + 2y = 300
∴ दो चरों वाली रैखिक समीकरण युग्म है
2x + y = 160
और 4x + 2y = 300
आलेखीय स्थिति में
2x + y = 160
2x = 160 – y
x = \(\frac{160-y}{2}\) ………………(1)
![]()
x = \(\frac{160-0}{2}=\frac{160}{2}\) = 80
y = 60 को (1) में प्रतिस्थापित करने पर हमें प्राप्त होता
x = \(\frac{160-60}{2}=\frac{100}{2}\) = 50
y = 160 को (1) में प्रतिस्थापित करने पर हमें प्राप्त होता है
x = \(\frac{160-160}{2}=\frac{0}{2}\) = 0
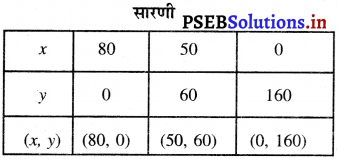
बिंदुओं A (80, 0), B (50, 60), C (0, 160) को आलेखित करने और उन्हें मिलाते हुए रेखा खींचने पर हमें समीकरण
2x + y = 160 का आलेख प्राप्त होता है
4x + 2y = 300
2x + y = 150
2x = 150 – y
x = \(\frac{150-y}{2}\) ……………(2)
y = 0 को (2), में प्रतिस्थापित करने पर हमें प्राप्त होता है
x = \(\frac{150-0}{2}=\frac{150}{2}\) = 75
y = 50 को (2) में प्रतिस्थापित करने पर हमें प्राप्त होता है
x = \(\frac{150-50}{2}=\frac{100}{2}\) = 50
y = 150 को (2) में प्रतिस्थापित करने पर हमें प्राप्त होता है
x = \(\frac{150-150}{2}=\frac{0}{2}\)
= 0
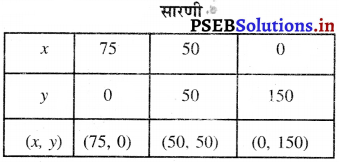
बिंदुओं D (75, 0), E (50, 50), F (0, 150) को आलेखित करने और उन्हें मिलाते हुए रेखा खींचने पर हमें समीकरण 4x + 2y = 300 का आलेख प्राप्त होता है।
आलेख से स्पष्ट है कि दोनों रेखाएँ कहीं पर भी प्रतिच्छेद नहीं करती अर्थात् वे समांतर हैं।
![]()