Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 3 ਦੋ ਚਲਾਂ ਵਿੱਚ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦੇ ਜੋੜੇ Ex 3.2 Textbook Exercise Questions and Answers.
PSEB Solutions for Class 10 Maths Chapter 3 ਦੋ ਚਲਾਂ ਵਿੱਚ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦੇ ਜੋੜੇ Exercise 3.2
1. ਹੇਠਾਂ ਦਿੱਤੀਆਂ ਸਮੱਸਿਆਵਾਂ ਵਿੱਚ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦੇ ਜੋੜੇ ਬਣਾਉ ਅਤੇ ਉਹਨਾਂ ਦੇ ਗ੍ਰਾਫੀ (ਆਲੇਖੀ) ਵਿਧੀ ਨਾਲ ਹੱਲ ਪਤਾ ਕਰੋ ।
ਪ੍ਰਸ਼ਨ (i).
ਜਮਾਤ X ਦੇ 10 ਵਿਦਿਆਰਥੀਆਂ ਨੇ ਗਣਿਤ ਦੀ ਇੱਕ ਬੁਝਾਰਤ ਮੁਕਾਬਲੇ ਵਿਚ ਭਾਗ ਲਿਆ । ਜੇਕਰ ਲੜਕੀਆਂ ਦੀ ਗਿਣਤੀ, ਲੜਕਿਆਂ ਦੀ ਗਿਣਤੀ ਤੋਂ 4 ਵੱਧ ਹੋਵੇ ਤਾਂ ਮੁਕਾਬਲੇ ਵਿਚ ਭਾਗ ਲੈਣ ਵਾਲੇ ਲੜਕੇ ਅਤੇ ਲੜਕੀਆਂ ਦੀ ਗਿਣਤੀ ਪਤਾ ਕਰੋ ।
ਉੱਤਰ:
ਮੰਨ ਲਉ – ਮੁਕਾਬਲੇ ਵਿਚ ਲੜਕਿਆਂ ਦੀ ਗਿਣਤੀ = x
ਅਤੇ ਮੁਕਾਬਲੇ ਵਿਚ ਲੜਕੀਆਂ ਦੀ ਗਿਣਤੀ = y
ਮੁਕਾਬਲੇ ਵਿੱਚ ਭਾਗ ਲੈਣ ਵਾਲੇ ਕੁੱਲ ਵਿਦਿਆਰਥੀ = 10
∴ x + y = 10
ਜਾਂ x + y – 10 = 0
ਪ੍ਰਸ਼ਨ ਅਨੁਸਾਰ
y = x + 4
ਜਾਂ x = y – 4
ਹੁਣ, ਰੇਖੀ ਸਮੀਕਰਣਾਂ ,
x + y = 10
ਅਤੇ x – y + 4 = 0 ਦਾ ਗ੍ਰਾਫ ਖਿੱਚੋ ।
x + y = 10
ਜਾਂ x = 10 – y …..(1)
y = 0 ਨੂੰ (1) ਵਿੱਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
x = 10 – 0 = 10
y = 7 ਨੂੰ (1) ਵਿੱਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
x = 10 – 7 = 3
y = 10 ਨੂੰ (1) ਵਿੱਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
x = 10 – 10 = 0 .
ਸਾਰਣੀ
ਬਿੰਦੂਆਂ A (10, 0), B (3, 7), C (0, 10) ਨੂੰ ਆਖਿਤ ਕਰਨ ‘ਤੇ ਅਤੇ ਉਹਨਾਂ ਨੂੰ ਮਿਲਾਉਂਦੇ ਹੋਏ ਰੇਖਾ ਖਿੱਚਣ ‘ਤੇ ਸਾਨੂੰ ਸਮੀਕਰਣ x + y = 10 ਦਾ ਗ੍ਰਾਫ਼ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
x – y + 4 = 0
ਜਾਂ x = y – 4 ….(2)
y = 0 ਨੂੰ (2) ਵਿੱਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
x = 0 – 4 = -4
y = 7 ਨੂੰ (2) ਵਿਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਮਿਲਦਾ ਹੈ ।
x = 7 – 4 = 3
y = 4 ਨੂੰ (2) ਵਿਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਮਿਲਦਾ ਹੈ ।
x = 4 – 4 = 0
ਸਾਰਣੀ

ਬਿੰਦੁਆਂ D (-4, 0), B (3, 7), E (0, 4) ਨੂੰ ਆਲੇਖਿਤ ਕਰਨ ਅਤੇ ਉਹਨਾਂ ਨੂੰ ਮਿਲਾਉਂਦੇ ਹੋਏ ਰੇਖਾ ਖਿੱਚਣ ‘ਤੇ ਸਾਨੂੰ ਸਮੀਕਰਣ x – y + 4 = 0 ਦਾ ਗ੍ਰਾਫ਼ ਆਲੇਖ) ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
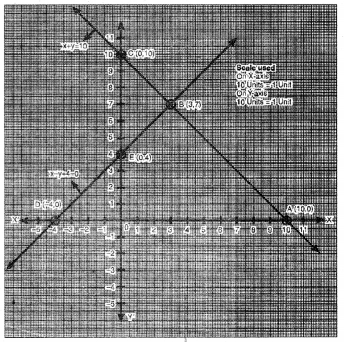
ਆਲੇਖ ਤੋਂ ਇਹ ਸਪੱਸ਼ਟ ਹੈ ਕਿ ਦੋਵੇਂ ਰੇਖੀ ਸਮੀਕਰਣਾਂ | ਬਿੰਦੂ B (3, 7) ਉੱਤੇ ਮਿਲਦੀਆਂ ਹਨ ।
∴ ਬਿੰਦੂ B (3, 7) ਆਲੇਖੀ ਸਥਿਤੀ ਹੈ ।
ਮੁਕਾਬਲੇ ਵਿਚ ਲੜਕਿਆਂ ਦੀ ਗਿਣਤੀ = 3
ਮੁਕਾਬਲੇ ਵਿਚ ਲੜਕੀਆਂ ਦੀ ਗਿਣਤੀ = 7
ਪ੍ਰਸ਼ਨ (ii).
5 ਪੈਨਸਿਲਾਂ ਅਤੇ 7 ਕਲਮਾਂ ਦਾ ਮੁੱਲ ₹ 50 ਹੈ, ਜਦ ਕਿ 7 ਪੈਨਸਿਲਾਂ ਅਤੇ 5 ਕਲਮਾਂ ਦਾ ਮੁੱਲ ₹ 46 ਹੈ । ਇਕ ਪੈਨਸਿਲ ਅਤੇ ਇਕ ਕਲਮ ਦਾ ਮੁੱਲ ਪਤਾ ਕਰੋ ।
ਉੱਤਰ:
ਮੰਨ ਲਉ 1 ਪੈਨਸਿਲ ਦਾ ਮੁੱਲ = ₹ 2
ਅਤੇ 1 ਕਲਮ ਦਾ ਮੁੱਲ = ₹ y
ਪਹਿਲੀ ਸ਼ਰਤ ਅਨੁਸਾਰ
5x + 7y = 50
ਦੂਸਰੀ ਸ਼ਰਤ ਅਨੁਸਾਰ
7x + 5y = 46
∴ ਰੇਖੀ ਸਮੀਕਰਣ ਜੋੜਾ ਹੈ :
5x + 7y = 50
7x + 5y = 46
ਹੁਣ, ਇਨ੍ਹਾਂ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦਾ ਆਲੇਖ ਖਿੱਚੋ !
5x + 7y = 50
ਜਾਂ 5x = 50 – 7y
ਜਾਂ x = \(\frac{50-7 y}{5}\) …(1)
y = 0 ਨੂੰ (1) ਵਿੱਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :

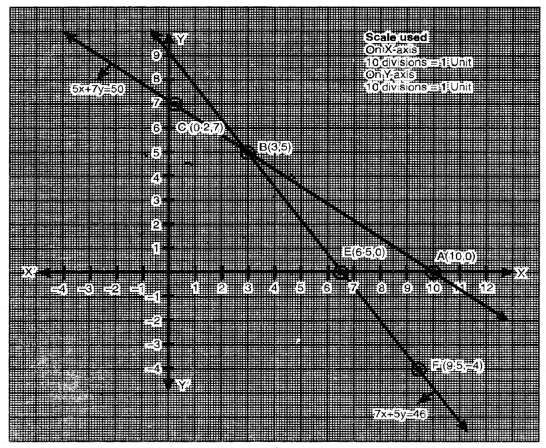
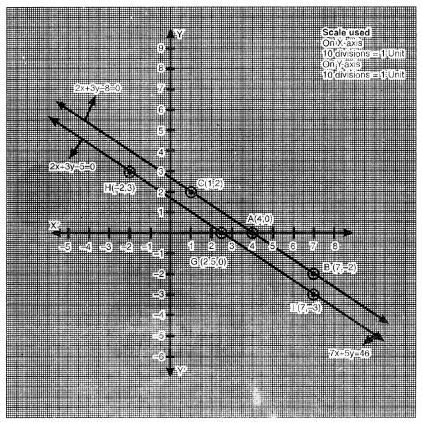
ਬਿੰਦੁਆਂ A (10, 0), B (3, 5), C (0.2, 7) ਨੂੰ । ਆਲੇਖਿਤ ਕਰਨ ਅਤੇ ਉਨ੍ਹਾਂ ਨੂੰ ਮਿਲਾਉਣ ‘ਤੇ ਸਾਨੂੰ ਸਮੀਕਰਣ 5x + 7y =50 ਦਾ ਆਲੇਖ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
7x + 5y = 46
ਨੂੰ 7x = 46 – 5y

ਬਿੰਦੂਆਂ E (6.5, 0), B (3, 5), F (9.5, – 4) ਨੂੰ ਆਲੇਖਿਤ ਕਰਨ ਅਤੇ ਉਨ੍ਹਾਂ ਨੂੰ ਮਿਲਾਉਂਦੇ ਹੋਏ ਰੇਖਾ ਖਿੱਚਣ ‘ਤੇ ਸਾਨੂੰ ਸਮੀਕਰਣ 7x + 5y = 46 ਦਾ ਆਲੇਖ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
ਆਲੇਖ ਤੋਂ ਇਹ ਸਪੱਸ਼ਟ ਹੈ ਕਿ ਦੋਵੇਂ ਰੇਖੀ ਸਮੀਕਰਣ ਬਿੰਦੂ B (3, 5) ਤੇ ਮਿਲਦੇ ਹਨ ।
∴ ਬਿੰਦੂ B (3, 5) ਆਲੇਖੀ ਸਥਿਤੀ ਹੈ ।
ਇਕ ਪੈਨਸਿਲ ਦਾ ਮੁੱਲ = ₹ 3
ਇਕ ਕਲਮ ਦਾ ਮੁੱਲ = ₹ 5
![]()
2. ਅਨੁਪਾਤਾਂ \(\frac{a_{1}}{a_{2}}\), \(\frac{b_{1}}{b_{2}}\) ਅਤੇ \(\frac{c_{1}}{c_{2}}\) ਦੀ ਤੁਲਨਾ ਕਰਕੇ ਪਤਾ ਕਰੋ ਕਿ ਹੇਠਾਂ ਦਿੱਤੇ ਸਮੀਕਰਣ ਜੋੜਿਆਂ ਦੁਆਰਾ ਦਰਸਾਉਂਦੀਆਂ ਰੇਖਾਵਾਂ, ਇੱਕ ਬਿੰਦੂ ’ਤੇ ਕੱਟਦੀਆਂ ਹਨ, ਸਮਾਂਤਰ ਹਨ ਜਾਂ ਸੰਪਾਤੀ ਹਨ :
ਪ੍ਰਸ਼ਨ (i).
5x – 4y + 8 = 0
7x + 6y – 9 = 4
ਉੱਤਰ:
ਦਿੱਤਾ ਗਿਆ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦਾ ਜੋੜਾ ਹੈ :
5x – 4y + 8 = 0
ਅਤੇ 7x + 6y – 9 = 0
ਇੱਥੇ a1 = 5, b1 = – 4, c1 = 8
a2 = 7, b2 = 6, c2 = – 9
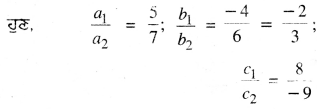
∴ \(\frac{a_{1}}{a_{2}}\) ≠ \(\frac{b_{1}}{b_{2}}\) ≠ \(\frac{c_{1}}{c_{2}}\)
ਇਸ ਲਈ ਦਿੱਤਾ ਗਿਆ ਸਮੀਕਰਣਾਂ ਦਾ ਜੋੜਾ ਇੱਕ ਬਿੰਦੂ ਉੱਤੇ ਕੱਟਦਾ ਹੈ ।
ਪ੍ਰਸ਼ਨ (ii).
9x + 3y + 12 = 0
18x + 6y + 24 = 0
ਉੱਤਰ:
ਦਿੱਤਾ ਗਿਆ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦਾ ਜੋੜਾ ਹੈ :
9x + 3y + 12 = 0
ਅਤੇ 18x + 6y + 24 = 0
ਇੱਥੇ a1 = 9, b1 = 3, c1 = 12
a2 = 18, b2 = 6, c2 = 24
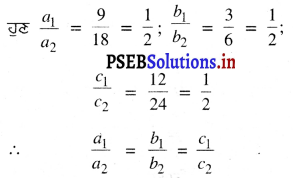
ਇਸ ਲਈ ਦਿੱਤਾ ਗਿਆ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦਾ ਜੋੜਾ ਸੰਪਾਤੀ ਹੈ ।
![]()
ਪ੍ਰਸ਼ਨ (iii).
6x – 3y + 10 = 0
2x – y + 9 = 0
ਉੱਤਰ:
ਦਿੱਤਾ ਗਿਆ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦਾ ਜੋੜਾ ਹੈ :
6x – 3y + 10 = 0,
ਅਤੇ 2x – y + 9 = 0
ਇੱਥੇ a1 = 6, b1 = -3, c1 = 10
a2 = 2, b2 = -1, c2 = 9
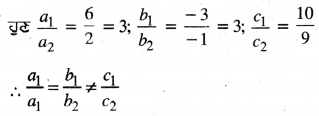
ਇਸ ਲਈ ਦਿੱਤਾ ਗਿਆ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦਾ ਜੋੜਾ । ਇੱਕ-ਦੂਜੇ ਦੇ ਸਮਾਂਤਰ ਹੈ ।
3. ਅਨੁਪਾਤਾਂ \(\frac{a_{1}}{a_{2}}\), \(\frac{b_{1}}{b_{2}}\) ਅਤੇ \(\frac{c_{1}}{c_{2}}\) ਦੀ ਤੁਲਨਾ ਕਰਕੇ ਪਤਾ ਕਰੋ ਕਿ ਹੇਠਾਂ ਦਿੱਤੇ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦੇ ਜੋੜੇ ਸੰਗਤ ਹਨ ਜਾਂ ਅਸੰਗਤ :
ਪ੍ਰਸ਼ਨ (i).
3x + 2y = 5; 2x – 3y = 7
ਉੱਤਰ:
ਦਿੱਤਾ ਗਿਆ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦਾ ਜੋੜਾ ਹੈ :
3x + 2y = 5
ਅਤੇ 2x – 3y = 7
ਜਾਂ 3x + 2y – 5 = 0
ਅਤੇ 2x – 3y – 7 = 0
ਇੱਥੇ a1 = 3, b1 = 2, c1 = – 5
a2 = 2, b2 = – 3, c2 = – 7
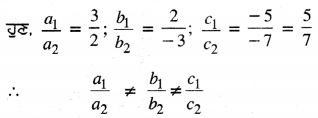
ਇਸ ਲਈ ਦਿੱਤਾ ਗਿਆ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦਾ ਜੋੜਾ ਸੰਗਤ ਹੈ ।
![]()
ਪ੍ਰਸ਼ਨ (ii).
2x – 3y = 8; 4x – 6y = 9
ਉੱਤਰ:
ਦਿੱਤਾ ਗਿਆ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦਾ ਜੋੜਾ ਹੈ :
2x – 3y = 8
ਅਤੇ 4x – 6y = 9
ਜਾਂ 2x – 3y – 8 = 0
4x – 6y – 9 = 0
ਇੱਥੇ a1 = 2, b1 = – 3, c1 = – 8
a2 = 4, b2 = – 6, c2 = -9

ਇਸ ਲਈ ਦਿੱਤਾ ਗਿਆ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦਾ ਜੋੜਾ ਅਸੰਗਤ ਹੈ ।
ਪ੍ਰਸ਼ਨ (iii).
\(\frac{3}{2}\)x + \(\frac{5}{3}\)y = 7; 9x – 10y = 14
ਉੱਤਰ:
ਦਿੱਤਾ ਗਿਆ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦਾ ਜੋੜਾ ਹੈ :
\(\frac{3}{2}\)x + \(\frac{5}{3}\)y = 7
ਅਤੇ 9x – 10y = 14
ਜਾਂ \(\frac{3}{2}\)x + \(\frac{5}{3}\)y – 7 = 0
ਅਤੇ 9x – 10y – 14 = 0
ਇੱਥੇ a1 = \(\frac{3}{2}\), b1 = \(\frac{5}{3}\), c1 = -7
a2 = 9, b2 = – 10, c2 = – 14
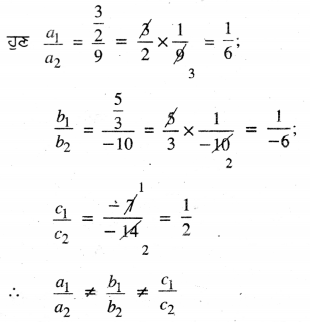
ਇਸ ਲਈ ਦਿੱਤਾ ਗਿਆ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦਾ ਜੋੜਾ ਸੰਗਤ ਹੈ ।
![]()
ਪ੍ਰਸ਼ਨ (iv).
5x – 3y = 11; -10x + 6y = – 22
ਉੱਤਰ:
ਦਿੱਤਾ ਗਿਆ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦਾ ਜੋੜਾ ਹੈ :
5x – 3y = 11
ਅਤੇ -10x + 6y = – 22
ਜਾਂ 5x – 3y – 11 = 0
ਅਤੇ -10x + 6y + 22 = 0
ਇੱਥੇ a1 = 5, b1 = -3, c1 = – 11
a2 = – 10, b2 = 6, c2 = 22
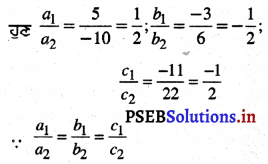
ਇਸ ਲਈ ਦਿੱਤਾ ਗਿਆ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦਾ ਜੋੜਾ ਸੰਗਤ ਹੈ ।
ਪ੍ਰਸ਼ਨ (v).
\(\frac{4}{3}\)x + 2y = 8; 2x + 3y = 12
ਉੱਤਰ:
ਦਿੱਤਾ ਗਿਆ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦਾ ਜੋੜਾ ਹੈ :
\(\frac{4}{3}\)x + 2y = 8 ਅਤੇ 2x + 3y = 12
ਅਤੇ \(\frac{4}{3}\)x + 2y – 8 = 0
ਜਾਂ 2x + 3y – 12 = 0
ਇੱਥੇ a1 = \(\frac{4}{3}\), b1 = 2, c1 = -12 .
a2 = 2, b2 = 3, c2 = – 12
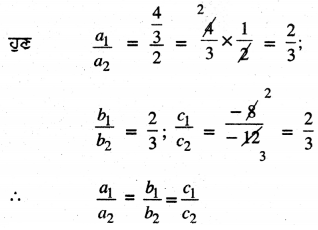
ਇਸ ਲਈ ਦਿੱਤਾ ਗਿਆ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦਾ ਜੋੜਾ ਸੰਗਤ ਹੈ ।
![]()
4. ਹੇਠਾਂ ਦਿੱਤੇ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦੇ ਜੋੜਿਆਂ ਵਿੱਚ ਕਿਹੜਾ ਜੋੜਾ ਸੰਗਤ ਹੈ ਅਤੇ ਕਿਹੜਾ ਅਸੰਗਤ ਜੇਕਰ ਜੋੜਾ ਸੰਗਤ ਹੈ ਤਾਂ ਆਲੇਖੀ (ਫੀ) ਵਿਧੀ ਨਾਲ ਹੱਲ ਪਤਾ ਕਰੋ :
ਪ੍ਰਸ਼ਨ (i).
x + y = 5, 2x + 2y = 10
ਉੱਤਰ:
ਦਿੱਤਾ ਗਿਆ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦਾ ਜੋੜਾ ਹੈ :
x + y = 5
ਅਤੇ 2x + 2y = 10
ਜਾਂ x + y – 5 = 0
2x + 2y – 10 = 0
ਇੱਥੇ a1 = 1, b1 = 1, c1 = -5
a2 = 2, b2 = 2, c2 = – 10

∴ ਦਿੱਤੀ ਹੋਈ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦੇ ਜੋੜੇ ਦਾ ਆਲੇਖ | ਖਿੱਚੋ
x + y = 5
x = 5 – y …..(1)
y = 0 ਨੂੰ (1) ਵਿੱਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
x = 5 – 0 = 5
y = 3 ਨੂੰ (1) ਵਿੱਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
x = 5 – 3 = 2
y = 5 ਨੂੰ (1) ਵਿੱਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
x = 5 – 5 = 0
ਸਾਰਣੀ
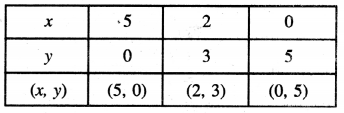
ਬਿੰਦੂਆਂ A (5, 0), B (2, 3), C (0, 5) ਨੂੰ ਆਲੇਖਿਤ ਕਰਨ ਅਤੇ ਉਹਨਾਂ ਨੂੰ ਮਿਲਾਉਣ ਤੇ ਸਾਨੂੰ ਸਮੀਕਰਣ x + y = 5 ਦਾ ਆਲੇਖ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
2x + 2y = 10 ਜਾਂ 2 (x + y) = 10
ਜਾਂ x + y = 5
ਜਾਂ x = 5 – …(2)
y = 0 ਨੂੰ (1) ਵਿੱਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
x = 5 – 0 = 5
y = 2 ਨੂੰ (2) ਵਿੱਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
x = 5 – 2 = 3
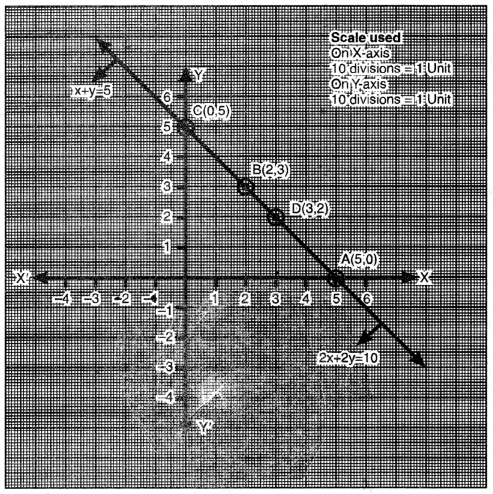
ਬਿੰਦੂਆਂ A (5, 0), D (3, 2), C (0, 5) ਨੂੰ ਆਲੇਖਿਤ ਕਰਨ ਅਤੇ ਉਹਨਾਂ ਨੂੰ ਮਿਲਾਉਣ ਤੇ ਸਾਨੂੰ ਸਮੀਕਰਣ 2x + 2y = 10 ਦਾ ਆਲੇਖ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
ਆਲੇਖ ਤੋਂ ਇਹ ਸਪੱਸ਼ਟ ਹੈ ਕਿ ਦਿੱਤਾ ਗਿਆ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦਾ ਜੋੜਾ ਸੰਪਾਤੀ, ਅਤੇ ਇਨ੍ਹਾਂ ਦੇ ਅਨੇਕ ਹੱਲ ਹਨ !
ਪ੍ਰਸ਼ਨ (ii).
x – y = 8, 3x – 3y = 16
ਉੱਤਰ:
ਦਿੱਤਾ ਗਿਆ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦਾ ਜੋੜਾ ਹੈ :
x – y = 8
ਅਤੇ 3x – 3y = 16
ਜਾਂ x – y – 8 = 0
ਅਤੇ 3x – 3y – 16 = 0
ਇੱਥੇ a1 =1, b1 = -1 , c1 = – 8
a2 = 3, b2 = – 3, c2 = – 16
y = 5 ਨੂੰ (2) ਵਿੱਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
x = 5 – 5 = 0
ਸਾਰਣੀ
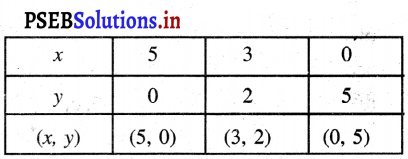
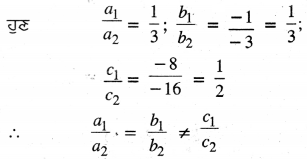
ਇਸ ਲਈ ਦਿੱਤਾ ਗਿਆ ਰੇਖੀ ਮੀਕਣਾਂ ਦਾ ਹੋ ਅਸੰਗਤ ਹੈ ।
![]()
ਪ੍ਰਸ਼ਨ (iii).
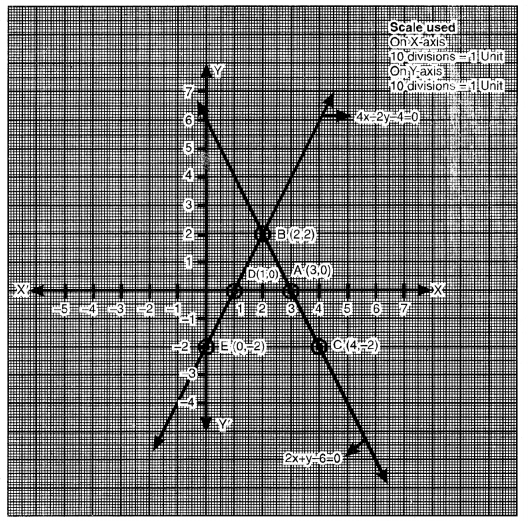
2x + y – 6 = 0, 4x – 2y – 4 = 0
ਉੱਤਰ:
ਦਿੱਤਾ ਗਿਆ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦਾ ਜੋੜਾ ਹੈ :
2x + y – 6 = 0
ਅਤੇ 4x – 2y – 4 = 0
ਇੱਥੇ a1 = 2, b1 = 1, c1 = 6
a2 = 4, b2 = -2, c2 = -4
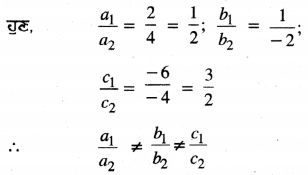
∴ ਦਿੱਤੇ ਗਏ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦੇ ਜੋੜੇ ਦਾ ਗ੍ਰਾਫ ਖਿੱਚੋ :
2x + y – 6 = 0
ਜਾਂ 2x = 6 – y
ਜਾਂ y = \(\frac{6-y}{2}\) ….(1)
y = 0 ਨੂੰ (1) ਵਿੱਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
x = \(\frac{6-0}{2}\) = \(\frac{6}{2}\) = 3
y = 2 ਨੂੰ (1), ਵਿੱਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
x = \(\frac{6-2}{2}\)
= \(\frac{4}{2}\) = 2
y = -2 ਨੂੰ (1) ਵਿੱਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
x = \(\frac{6-(-2)}{2}\) = \(\frac{6+2}{2}\)
= \(\frac{8}{2}\) = 4
ਸਾਰਣੀ
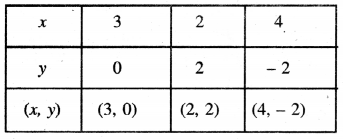
ਬਿੰਦੂਆਂ A (3, 0), B (2, 2), C (4, – 2) ਨੂੰ ਆਖਿਤ ਕਰਨ ‘ਤੇ ਉਨ੍ਹਾਂ ਨੂੰ ਮਿਲਾਉਂਦੇ ਹੋਏ ਰੇਖਾ ਖਿਚਣ ‘ਤੇ ਸਮੀਕਰਣ 2x +y – 6 = 0 ਦਾ ਆਲੇਖ ਮਿਲਦਾ ਹੈ ।
4x – 2y – 4 = 0
ਜਾਂ 2[2x – y – 2] = 0
ਜਾਂ 2x – y – 2 = 0
ਜਾਂ 2x = y + 2
ਜਾਂ x = \(\frac{y+2}{2}\) …(2)
y = 0 ਨੂੰ (2) ਵਿੱਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
x = \(\frac{0+2}{2}\) = \(\frac{2}{2}\) = 1
y = 2 ਨੂੰ (2) ਵਿੱਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
x = \(\frac{2+2}{2}\) = \(\frac{4}{2}\) = 2
y = -2 ਨੂੰ (2) ਵਿੱਚ ਰੱਖਣ ‘ਤੇ ਸ਼ਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
x = \(\frac{-2+2}{2}\)
= \(\frac{0}{2}\) = 0
ਸਾਰਣੀ
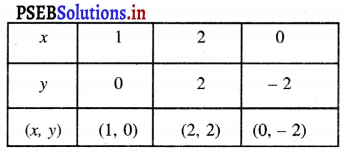
ਬਿੰਦੂਆਂ D (1, 0), B (2, 2), E (0, -2) ਨੂੰ ਆਲੇਖਿਤ ਕਰਨ ‘ਤੇ ਉਨ੍ਹਾਂ ਨੂੰ ਮਿਲਾਉਂਦੇ ਹੋਏ ਰੇਖਾ ਖਿਚਣ ‘ਤੇ ਸਾਨੂੰ ਸਮੀਕਰਣ 4x – 2y -4 = 0 ਦਾ ਆਲੇਖ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
ਆਲੇਖ ਤੋਂ ਇਹ ਸਪੱਸ਼ਟ ਹੈ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦਾ ਜੋੜਾ ਬਿੰਦੂ B (2, 2) ਉੱਤੇ ਮਿਲਦਾ ਹੈ ।
∴ ਦਿੱਤੀ ਹੋਈ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦਾ ਜੋੜਾ ਵਿਲੱਖਣ ਹੈ ।
ਪ੍ਰਸ਼ਨ (iv).
2x – 2y – 2 = 0, 4x – 4y – 5 = 0
ਉੱਤਰ:
ਦਿੱਤਾ ਗਿਆ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦਾ ਜੋੜਾ ਹੈ :
2x – 2y – 2 = 0
ਅਤੇ 4x – 4y – 5 = 0
ਇੱਥੇ a1 = 2, b1 = – 2, c1 = – 2
a2 = 4, b2 = – 4, c2 = – 5
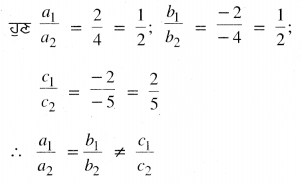
ਇਸ ਲਈ ਦਿੱਤਾ ਗਿਆ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦਾ ਜੋੜਾ ਅਸੰਗਤ ਹੈ ।
![]()
ਪ੍ਰਸ਼ਨ 5.
ਇੱਕ ਆਇਤਾਕਾਰ ਬਾਗ, ਜਿਸਦੀ ਲੰਬਾਈ, ਚੌੜਾਈ ਤੋਂ 4 ਮੀ. ਵੱਧ ਹੈ, ਦਾ ਅਰਧ ਪਰਿਮਾਪ 36 ਮੀ. ਹੈ । ਬਾਗ ਦੀ ਲੰਬਾਈ ਅਤੇ ਚੌੜਾਈ ਪਤਾ ਕਰੋ ।
ਹੱਲ :
ਮੰਨ ਲਓ ਬਾਗ ਦੀ ਲੰਬਾਈ = x ਮੀ.
ਬਾਗ ਦੀ ਚੌੜਾਈ = y ਮੀ.
ਬਾਗ ਦਾ ਪਰਿਮਾਪ = 2 [x + y] ਮੀ.
ਬਾਗ ਦਾ ਅਰਧ ਪਰਿਮਾਪ = (x + y) ਮੀ
ਪ੍ਰਸ਼ਨ ਦੀ ਪਹਿਲੀ ਸ਼ਰਤ ਅਨੁਸਾਰ
x = y + 4
ਪ੍ਰਸ਼ਨ ਦੀ ਦੂਸਰੀ ਸ਼ਰਤ ਅਨੁਸਾਰ
x + y = 36
∴ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦਾ ਜੋੜਾ ਹੈ :
x = y + 4
ਅਤੇ x + y = 36
x = y + 4 …(1)
y = 0 ਨੂੰ (1) ਵਿੱਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
x = 0 + 4 = 4
y = -4 ਨੂੰ (1) ਵਿੱਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
x = – 4 + 4 = 0
y = 16 ਨੂੰ (1) ਵਿੱਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
x = 16 + 4 = 20
ਸਾਰਣੀ
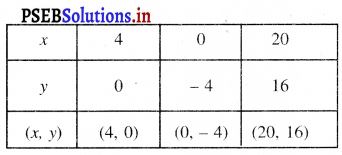
ਬਿੰਦੁਆਂ A (4, 0), B (0, – 4), C (20, 16) ਨੂੰ ਆਲੇਖਿਤ ਕਰਨ ਤੇ ਅਤੇ ਉਹਨਾਂ ਨੂੰ ਮਿਲਾਉਂਦੇ ਹੋਏ ਰੇਖਾ ਖਿੱਚਣ ‘ਤੇ ਸਾਨੂੰ ਸਮੀਕਰਣ x = y + 4 ਦਾ ਆਲੇਖ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
x + y = 36
x = 36 – y …..(2)
y = 12 ਨੂੰ (2) ਵਿੱਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
x = 36 – 12 = 24
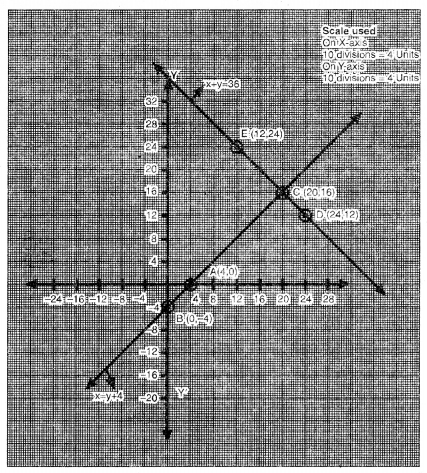
ਆਲੇਖ ਤੋਂ ਇਹ ਸਪੱਸ਼ਟ ਹੈ ਕਿ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦਾ ਜੋੜਾ ਬਿੰਦੂ C (20, 16) ਤੇ ਮਿਲਦਾ ਹੈ ।
∴ C (20, 16) ਭਾਵ x = 20 ਅਤੇ y = 16 ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦੇ ਜੋੜੇ ਦਾ ਹੱਲ ਹੈ ।
∴ ਬਾਗ ਦੀ ਲੰਬਾਈ = 20 ਮੀ.
ਬਾਗ ਦੀ ਚੌੜਾਈ = 16 ਮੀ. ||
y = 24 ਨੂੰ (2) ਵਿੱਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
x = 36 – 24 = 12
y = 16 ਨੂੰ (2) ਵਿੱਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
x = 36 – 16 = 20
ਸਾਰਣੀ
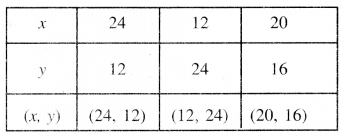
ਬਿੰਦੂਆਂ D (24, 12), E ( 12, 24), C (20, 16) ਨੂੰ ਆਲੇਖਿਤ ਕਰਨ ‘ਤੇ ਉਹਨਾਂ ਨੂੰ ਮਿਲਾਉਂਦੇ ਹੋਏ ਰੇਖਾ ਖਿੱਚਣ ‘ਤੇ ਸਾਨੂੰ ਸਮੀਕਰਣ x + y = 36 ਦਾ ਆਲੇਖ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
ਇੱਕ ਹੋਰ ਵਿੱਧੀ
ਮੰਨ ਲਉ ਬਾਗ ਦੀ ਚੌੜਾਈ = x ਮੀ.
ਬਾਗ ਦੀ ਲੰਬਾਈ = (x + 4) ਮੀ.
ਬਾਗ ਦਾ ਪਰਿਮਾਪ = 2 ਲੰ: + ਚੌ:]
= 2 [x + x + 4] ਮੀ.
= 2 [2x + 4] ਮੀ.
∴ ਬਾਗ ਦਾ ਅਰਧ ਪਰਿਮਾਪੁ = (2x + 4)
ਪ੍ਰਸ਼ਨ ਅਨੁਸਾਰ
2x + 4 = 36
ਜਾਂ 2x = 36 – 4
ਜਾਂ 2x = 32
ਜਾਂ x = \(\frac{32}{2}\) = 16
∴ ਬਾਗ ਦੀ ਚੌੜਾਈ = 16 ਮੀ.
ਬਾਗ ਦੀ ਲੰਬਾਈ = (16 + 4) ਮੀ.
= 20 ਮੀ.
6. ਇਕ ਰੇਖੀ ਸਮੀਕਰਣ 2x + 3y – 8 = 9 ਦਿੱਤੀ ਗਈ । ਹੈ । ਦੋ ਚਲਾਂ ਵਿੱਚ ਇਕ ਇਸ ਤਰ੍ਹਾਂ ਦੀ ਰੇਖੀ ਸਮੀਕਰਣ ਲਿਖੋ ਤਾਂ ਕਿ ਪ੍ਰਾਪਤ ਜੋੜੇ ਦਾ ਜਿਮਾਇਤੀ ਰੂਪ
ਪ੍ਰਸ਼ਨ (i).
ਕੱਟਦੀਆਂ ਰੇਖਾਵਾਂ ਹੋਣ ।
ਉੱਤਰ:
ਸਥਿਤੀ (i) ਕੱਟਦੀਆਂ ਰੇਖਾਵਾਂ
ਦਿੱਤੀ ਹੋਈ ਰੇਖੀ ਸਮੀਕਰਣ ਹੈ :
2x + 3y – 8 = 0 ….(1)
ਇੱਥੇ ਕਾਟਵੀਂ ਰੇਖਾਵਾਂ ਦੀ ਸ਼ਰਤਾਂ ਨੂੰ ਪੂਰਾ ਕਰਨ ਲਈ ਅਨੇਕ ਮੁੱਲ ਹਨ ।
ਭਾਵ \(\frac{a_{1}}{a_{2}}\) ≠ \(\frac{b_{1}}{b_{2}}\) ≠ \(\frac{c_{1}}{c_{2}}\)
ਇਨ੍ਹਾਂ ਵਿੱਚੋਂ ਇੱਕ ਹੈ ।
3x – 2y – 6 = 0 ….(2)
ਰੇਖੀ ਸਮੀਕਰਣਾਂ ( 1 ) ਅਤੇ (2) ਦਾ ਆਲੇਖ ਖਿੱਚੋ ।
2x + 3y – 8 = 0
ਜਾਂ 2x = 8 – 3y
ਜਾਂ x = \(\frac{8-3y}{2}\) …… (3)
y = 0 ਨੂੰ (3) ਵਿੱਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
x = \(\frac{8-30}{2}\) = \(\frac{8}{2}\) = 4
y = – 2 ਨੂੰ (3) ਵਿੱਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
x = \(\frac{8-3(-2)}{2}\) = \(\frac{14}{2}\) = 7
y = 2 ਨੂੰ (3) ਵਿੱਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
x = \(\frac{8-3×2}{2}\) = \(\frac{8-6}{2}\) = \(\frac{2}{2}\) = 1
ਸਾਰਣੀ
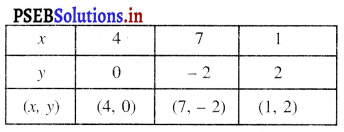
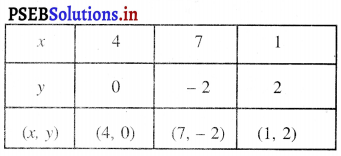
ਬਿੰਦੁਆਂ A (4, 0), B (7, – 2), C (1, 2) ਨੂੰ ਆਲੇਖਿਤ ਕਰਨ ‘ਤੇ ਅਤੇ ਉਹਨਾਂ ਨੂੰ ਮਿਲਾਉਣ ‘ਤੇ ਸਾਨੂੰ ਰੇਖਾ ਸਮੀਕਰਣ 2x + 3y – 8 = 9 ਦਾ ਆਲੇਖ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
3x – 2y – 6 = 0
ਜਾਂ 3x = 6 + 2y
ਜਾਂ x = \(\frac{6+2y}{3}\) …(4)
y = 0 ਨੂੰ (1) ਵਿੱਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
x = \(\frac{6+2×0}{3}\) = \(\frac{6}{3}\) = 2
y = – 3 ਨੂੰ (4) ਵਿੱਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
x = \(\frac{6+2(-3)}{3}\)
= \(\frac{6-6}{3}\) = 0
y = 3 ਨੂੰ (4) ਵਿਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
x = \(\frac{6+2×3}{3}\) = \(\frac{6+6}{3}\)
= \(\frac{12}{3}\) = 4
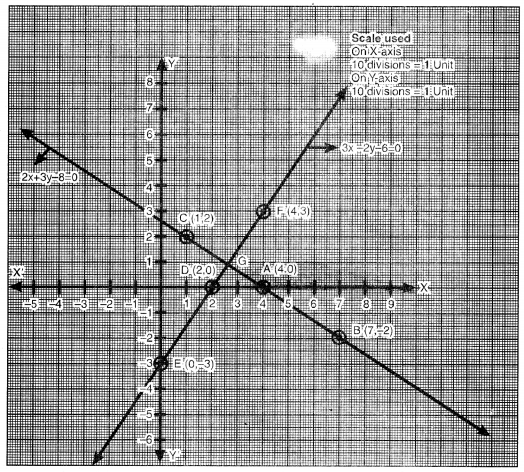
ਸਾਰਣੀ

ਬਿੰਦੂਆਂ D (2, 0), E (0, -3), F (4, 3) ਨੂੰ ਆ ਖਿਤ ਕਰਨ ‘ਤੇ ਅਤੇ ਉਹਨਾਂ ਨੂੰ ਮਿਲਾਉਂਦੇ ਹੋਏ ਰੇਖਾ ਖਿਚਣ ‘ਤੇ ਸਾਨੂੰ ਸਮੀਕਰਣ’ 3x – 2y – 6 = 0 ਦਾ ਆਲੇਖ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ !
ਆਲੇਖ ਤੋਂ ਇਹ ਸਪੱਸ਼ਟ ਹੈ ਕਿ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦਾ ਜੋੜਾ ਬਿੰਦੂ G ਉੱਤੇ ਕੱਟਦਾ ਹੈ ।
![]()
ਪ੍ਰਸ਼ਨ (ii).
ਸਮਾਂਤਰ ਰੇਖਾਵਾਂ ਹੋਣ ।
ਉੱਤਰ:
ਸਥਿਤੀ (ii) ਸਮਾਂਤਰ ਰੇਖਾਵਾਂ ਦਿੱਤੀ ਹੋਈ ਰੇਖੀ ਸਮੀਕਰਣ ਹੈ :
2x + 3y – 8 = 9 …(1)
ਇੱਥੇ ਦੋ ਚਲਾਂ ਵਾਲੀਆਂ ਹੋਰ ਵੀ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਹੋ
ਸਕਦੀਆਂ ਹਨ ਜੋ ਸਮਾਂਤਰ ਰੇਖਾਵਾਂ ਦੀ ਸ਼ਰਤ ਨੂੰ ਪੂਰਾ ਕਰਦੀਆਂ ਹਨ ਭਾਵ
\(\frac{a_{1}}{a_{2}}\) = \(\frac{b_{1}}{b_{2}}\) ≠ \(\frac{c_{1}}{c_{2}}\)
ਉਨ੍ਹਾਂ ਵਿੱਚੋਂ ਇੱਕ ਹੈ ।
2x + 3y – 5 = 0 ….(2)
ਹੁਣ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ( 1 ) ਅਤੇ (2) ਦਾ ਆਲੇਖ ਖਿੱਚੋ । ਰੇਖੀ ਸਮੀਕਰਣ 2x + 3 – 8 = 0 ਲਈ ਆਲੇਖ ਹੈ :
ਸਾਰਣੀ
2x + 3y – 5 = 0
ਜਾਂ 2x = 5 – 3y
ਜਾਂ x = \(\frac{5-3y}{2}\) …(3)
y = 0 ਨੂੰ (3) ਵਿੱਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
x = \(\frac{5-3×0}{2}\) = \(\frac{5}{2}\) = 2.5
ਸਾਰਣੀ

ਬਿੰਦੂਆਂ G (2.5, 0), H (- 2, 3), I (7, – 3) ਨੂੰ ਆਲੇਖਿਤ ਕਰਨ ‘ਤੇ ਅਤੇ ਮਿਲਾਉਂਦੇ ਹੋਏ ਰੇਖਾ ਖਿੱਚਣ ‘ਤੇ ਸਾਨੂੰ ਸਮੀਕਰਣ 2x + 3y – 5 = 0 ਦਾ ਆਲੇਖ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
y = 3 ਨੂੰ (3) ਵਿੱਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
y = \(\frac{5-3×3}{2}\) = \(\frac{5-9}{2}\) = \(\frac{-4}{2}\) = -2
y = -3 ਨੂੰ (3) ਵਿੱਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
x = \(\frac{5-3(-3)}{2}\) = \(\frac{5+9}{2}\) = \(\frac{14}{2}\)
= 7
ਪ੍ਰਸ਼ਨ (iii).
ਸੰਪਾਤੀ ਰੇਖਾਵਾਂ ਹੋਣ ।
ਉੱਤਰ:
ਸਥਿਤੀ (iii) ਸੰਪਾਤੀ ਰੇਖਾਵਾਂ ਲਈ
ਦਿੱਤੀ ਹੋਈ ਸਮੀਕਰਣ
2x + 3y – 8 = 0 ….(1)
ਦੋ ਚਲਾਂ ਵਿੱਚ ਅਜਿਹੇ ਹੋਰ ਵੀ ਰੇਖੀ ਸਮੀਕਰਣ ਹੋ ਸਕਦੇ ਹਨ ਜੋ ਸੰਪਾਤੀ ਰੇਖਾਵਾਂ ਦੀਆਂ ਸ਼ਰਤਾਂ ਨੂੰ ਸੰਤੁਸ਼ਟ ਕਰਦੇ ਹੋਣ ।
ਭਾਵ \(\frac{a_{1}}{a_{2}}\) = \(\frac{b_{1}}{b_{2}}\) = \(\frac{c_{1}}{c_{2}}\)
ਉਨ੍ਹਾਂ ਵਿਚ ਇਸ ਪ੍ਰਕਾਰ ਹੈ ।
6x + 9y – 24 = 0 ….(2)
ਹੁਣ ਰੇਖੀ (1) ਅਤੇ (2) ਦਾ ਆਲੇਖ ਖਿਚਣ ‘ਤੇ
ਰੇਖੀ ਸਮੀਕਰਣ (2) ਲਉ ॥
6x + 9y – 24 = 0
ਜਾਂ 3 [2x + 3y – 8] = 0
ਜਾਂ 2 + 3y – 8 = 0
∴ ਦੋਵਾਂ ਵਿਚ ਬਿੰਦੂ ਇਕ ਸਮਾਨ ਹਨ ਇਸ ਲਈ ਦੋਵੇਂ ਸਮੀਕਰਣਾਂ ਇਕ ਹੀ ਰੇਖਾ ਹਨ ।
![]()
ਪ੍ਰਸ਼ਨ 7.
ਸਮੀਕਰਣਾਂ x – y + 1 = 0 ਅਤੇ 3x + 2y – 12 = 0 ਦਾ ਗ੍ਰਾਫ਼ ਖਿੱਚੋ । x-ਧੁਰੇ ਅਤੇ ਇਨ੍ਹਾਂ ਰੇਖਾਵਾਂ ਨਾਲ ਬਣ ਤ੍ਰਿਭੁਜ ਦੇ ਸਿਖ਼ਰਾਂ ਦੇ ਨਿਰਦੇਸ਼ ਅੰਕ ਪਤਾ ਕਰੋ ਅਤੇ ਤਿਭੁਜ ਆਕਾਰ ਨੂੰ ਛਾਇਆ-ਅੰਕਿਤ (Shade) ਕਰੋ ।
ਹੱਲ :
ਇੱਕ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦਾ ਜੋੜਾ ਹੈ ।
x – y + 1 = 0
ਅਤੇ 3x + 2y – 12 = 0
x – y + 1 = 0
ਜਾਂ x = y – 1 ……(1)
y = 0 ਨੂੰ (1) ਵਿਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
x = 0 – 1 = – 1
y = 3 ਨੂੰ (1) ਵਿੱਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
x = 3 – 1 = 2
y = 1 ਨੂੰ ( 3 ) ਵਿੱਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
x = 1 – 1 = 0
ਸਾਰਣੀ

ਬਿੰਦੁਆਂ A -1, 0), B (2, 3), C (0, 1) ਨੂੰ ਆਲੇਖਿਤ ਕਰਨ ‘ਤੇ ਉਹਨਾਂ ਨੂੰ ਮਿਲਾਉਂਦੇ ਹੋਏ ਰੇਖਾ ਖਿੱਚਣ ‘ਤੇ ਸਾਨੂੰ ਸਮੀਕਰਣ x – y + 1 = 0 ਦਾ ਆਲੇਖ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
ਜਾਂ 3x + 2y – 12 = 0
3x = 12 – 2y
x = \(\frac{12-2y}{3}\) …….(2)
y = 0 ਨੂੰ (2) ਵਿੱਚ ਰੱਖਣ ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
x = \(\frac{12-2×0}{3}\) = \(\frac{12}{3}\) = 4
y = 3 ਨੂੰ (2), ਵਿੱਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
x = \(\frac{12-2×3}{3}\) = \(\frac{12-6}{3}\) = \(\frac{6}{3}\) = 2
y = 6 ਨੂੰ (2) ਵਿੱਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
x = \(\frac{12-2×6}{3}\) = \(\frac{12-12}{3}\) = 0
ਸਾਰਣੀ

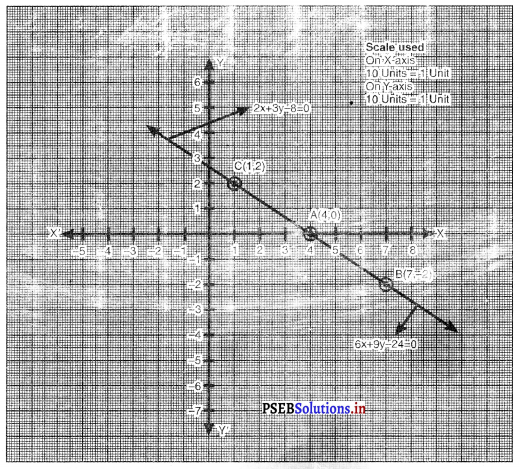
ਬਿੰਦੂਆਂ D (4, 0), B (2, 3), E (0, 6) ਨੂੰ ਆਲੇਖਿਤ ਕਰਨ ‘ਤੇ ਉਨ੍ਹਾਂ ਨੂੰ ਮਿਲਾਉਂਦੇ ਹੋਏ ਰੇਖਾ ਖਿੱਚਣ ‘ਤੇ ਸਾਨੂੰ ਸਮੀਕਰਣ 3x +2y – 12 = 0 ਦਾ ਆਲੇਖ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦੇ ਜੋੜੇ x-ਧੁਰੇ ਦੁਆਰਾ ਬਣਾਏ ਗਏ ਤਿਭੁਜ ਦੇ ਸਿਖ਼ਰਾਂ ਦੇ ਆਲੇਖ ਨੂੰ ਦਿਖਾਇਆ ਗਿਆ ਹੈ ।
∴ △ABD ਇਸ ਪ੍ਰਕਾਰ ਬਣੀ ਤ੍ਰਿਭੁਜ ਹੈ ।
△ABD ਦੇ ਸਿਖ਼ਰ ਹਨ : A (-1, 0), B (2, 3) ਅਤੇ D (4, 0).
ਹੁਣ, ਅਧਾਰ AD ਦੀ ਲੰਬਾਈ = AO + OD
= 1+ 4 = 5 ਇਕਾਈਆਂ
ਲੰਬ BF ਦੀ ਲੰਬਾਈ = 3 ਇਕਾਈਆਂ
∴ △ABD ਦਾ ਖੇਤਰਫਲ = \(\frac{1}{2}\) × ਅਧਾਰ × ਲੰਬ
= \(\frac{1}{2}\) × AD × BF
= (\(\frac{1}{2}\) × 5 × 3)
ਵਰਗ ਇਕਾਈਆਂ |
= \(\frac{15}{2}\) = 7.5
ਵਰਗ ਇਕਾਈਆਂ
