Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 3 ਦੋ ਚਲਾਂ ਵਿੱਚ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦੇ ਜੋੜੇ Ex 3.4 Textbook Exercise Questions and Answers.
PSEB Solutions for Class 10 Maths Chapter 3 ਦੋ ਚਲਾਂ ਵਿੱਚ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦੇ ਜੋੜੇ Exercise 3.4
1. ਹੇਠਾਂ ਦਿੱਤੇ ਸਮੀਕਰਣ ਜੋੜਿਆਂ ਨੂੰ ਵਿਲੋਪਣ ਵਿਧੀ ਅਤੇ ਪ੍ਰਤਿਸਥਾਪਨ ਵਿਧੀ ਨਾਲ ਹੱਲ ਕਰੋ ਕਿਹੜੀ ਵਿਧੀ ਵੱਧ ਉਚਿਤ ਹੈ ?
ਪ੍ਰਸ਼ਨ (i).
x + y = 5 ਅਤੇ 2x – 3y = 4
ਉੱਤਰ:
ਦਿੱਤਾ ਗਿਆ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦਾ ਜੋੜਾ ਹੈ :
x + y = 5 ….(1)
ਅਤੇ 2x – 3y = 4 ….(2)
ਵਿਲੋਪਣ ਵਿਧੀ
(1) ਨੂੰ 2, ਨਾਲ ਗੁਣਾਂ ਕਰਨ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
2x + 2y = 10 ….(3)
ਹੁਣ, (3) – (2) ਤੋਂ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
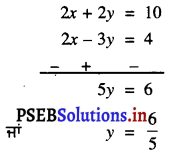
y ਦਾ ਇਹ ਮੁੱਲ (1) ਵਿਚ ਭਰਨ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ
x + \(\frac{6}{5}\) = 5
ਜਾਂ x = 5 – \(\frac{6}{5}\)
= \(\frac{25-6}{5}\) = \(\frac{19}{5}\)
ਹੁਣ, x = \(\frac{19}{5}\) ਅਤੇ \(\frac{6}{5}\)
ਪ੍ਰਤਿਸਥਾਪਨ ਵਿਧੀ
(2) ਤੋਂ 2x = 4 + 3y
ਜਾਂ x = \(\frac{4+3y}{2}\) ….(4)
x ਦਾ ਮੁੱਲ (1) ਵਿੱਚ ਪ੍ਰਤਿਸਥਾਪਿਤ ਕਰਨ ‘ਤੇ ਸਾਨੂੰ | ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
\(\frac{4+3y}{2}\) + y = 5
ਜਾਂ \(\frac{4+3y+2y}{2}\) = 5
ਜਾਂ 4 + 5y = 10
ਜਾਂ 5y = 10 – 4 = 6
ਜਾਂ y =\(\frac{6}{5}\)
y ਦਾ ਇਹ ਮੁੱਲ (4) ਵਿਚ ਪ੍ਰਤਿਸਥਾਪਿਤ ਕਰਨ ‘ਤੇ : ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
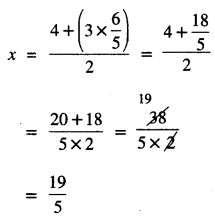
ਇਸ ਲਈ x = \(\frac{19}{5}\) ਅਤੇ y = \(\frac{6}{5}\)
ਪ੍ਰਸ਼ਨ (ii).
3x + 4y = 10 ਅਤੇ 2x – 2y = 2
ਉੱਤਰ:
ਦਿੱਤਾ ਗਿਆ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦਾ ਜੋੜਾ ਹੈ :
3x + 4y = 10 …….(1)
ਅਤੇ 2x – 2y = 2 ……..(2)
ਵਿਲੋਪਣ ਵਿਧੀ
ਸਮੀਕਰਣ (2) ਨੂੰ 2 ਨਾਲ ਗੁਣਾ ਕਰਨ ‘ਤੇ, ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
4x – 4y = 4 …(3)
ਹੁਣ, (3) + (1) ਤੋਂ
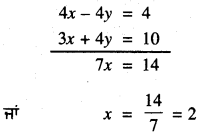
x ਦਾ ਇਹ ਮੁੱਲ (1) ਵਿੱਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
3 (2) + 4y = 10
ਜਾਂ 6 + 4y = 10
ਜਾਂ 4y = 10 – 6
ਜਾਂ 4y = 4
ਜਾਂ y = \(\frac{4}{4}\) = 1
∴ x = 2 ਅਤੇ y = 1
ਤਿਸਥਾਪਨ ਵਿਧੀ
(2) ਤੋਂ
2x = 2 + 2y
ਜਾਂ x = y + 1 . . …(3)
x ਦਾ ਇਹ ਮੁੱਲ (1) ਵਿੱਚ ਪ੍ਰਤਿਸਥਾਪਿਤ ਕਰਨ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
3 (y + 1) + 4y = 10
ਜਾਂ 3y + 3 + 4y = 10
ਜਾਂ 7y = 10 – 3
ਜਾਂ 7y = 7
ਜਾਂ y = 1
y ਦਾ ਇਹ ਮੁੱਲ (3) ਵਿੱਚ ਪ੍ਰਤਿਸਥਾਪਿਤ ਕਰਨ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
x = 1 + 1 = 2
∴ x = 2 ਅਤੇ y = 1
![]()
ਪ੍ਰਸ਼ਨ (iii).
3x – 5y – 4 = 0 ਅਤੇ 9x = 2y + 7
ਉੱਤਰ:
ਦਿੱਤਾ ਗਿਆ ਰੇਖੀ ਸਮੀਕਰਣ ਜੋੜਾ ਹੈ :
3x – 5y – 4 = 0 …(1)
ਅਤੇ 9x = 2y + 7
ਜਾਂ 9x – 2y – 7 = 0 ….(2)
ਵਿਲੋਪਣ ਵਿਧੀ
(1) ਨੂੰ 3 ਨਾਲ ਗੁਣਾ ਕਰਨ ‘ਤੇ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
9x – 15y – 12 = 0 …(3)
ਹੁਣ, (3) – (2) ਤੋਂ ਮਿਲਦਾ ਹੈ ।

y ਦਾ ਇਹ ਮੁੱਲ (1) ਵਿੱਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
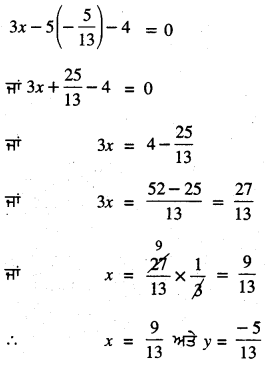
ਤਿਸਥਾਪਨ ਵਿਧੀ
(2) ਤੋਂ, x = \(\frac{2y+7}{9}\) …(4)
x ਦਾ ਮੁੱਲ (1) ਵਿੱਚ ਪ੍ਰਤਿਸਥਾਪਿਤ ਕਰਨ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
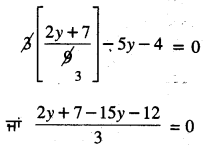
ਜਾਂ -13y – 5 = 0
ਜਾਂ -13y = 5
ਜਾਂ y = \(-\frac{5}{13}\)
y ਦਾ ਇਹ ਮੁੱਲ (4) ਵਿੱਚ ਪ੍ਰਤਿਸਥਾਪਿਤ ਕਰਨ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :

ਪ੍ਰਸ਼ਨ (iv).
\(\frac{x}{2}\) + \(\frac{2y}{3}\) -1 ਅਤੇ x – \(\frac{y}{3}\) = 3
ਉੱਤਰ:
ਦਿੱਤਾ ਗਿਆ ਰੇਖੀ ਸਮੀਕਰਣ ਜੋੜਾ ਹੈ :
\(\frac{x}{2}\) + \(\frac{2y}{3}\) = 1
ਜਾਂ \(\frac{3x+4y}{6}\) = -1
ਜਾਂ 3x + 4y = – 6 …(1)
x – \(\frac{y}{3}\) = 3
ਜਾਂ \(\frac{3x-y}{3}\) = 3
ਜਾਂ 3x – y = 9 …(2)
ਵਿਲੋਪਣ ਵਿਧੀ ।
(1) – (2) ਤੋਂ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
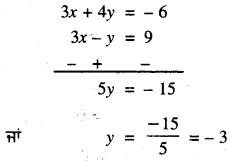
y ਦਾ ਇਹ ਮੁੱਲ (1) ਵਿੱਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ |
3x + 4(-3) = – 6
ਜਾਂ 3x – 12 = – 6
ਜਾਂ 3x = -6 + 12
ਜਾਂ 3x = 6
ਜਾਂ x = \(\frac{6}{3}\) = 2
∴ x = 2, y = -3
ਤਿਸਬਾਪਨ ਵਿਧੀ :
(2) ਤੋਂ, y = 3x – 9 …..(4)
y ਦਾ ਇਹ ਮੁੱਲ (1) ਵਿੱਚ ਪ੍ਰਤਿਸਥਾਪਿਤ ਕਰਨ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
3x + 4 (3x – 9) = – 6
ਜਾਂ 3x + 12x – 36 = – 6
ਜਾਂ 15x = – 6 + 36
ਜਾਂ 15x = 30
ਜਾਂ x = \(\frac{30}{15}\) = 2
x ਦਾ ਮੁੱਲ (4) ਵਿੱਚ ਪ੍ਰਤਿਸਥਾਪਿਤ ਕਰਨ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
y = 3 (2) – 9
= 6 – 9 = – 3
∴ x = 2, y = – 3
![]()
2. ਹੇਠਾਂ ਦਿੱਤੀਆਂ ਸਮੱਸਿਆਵਾਂ ਦੇ ਰੇਖੀ ਸਮੀਕਰਣ ਜੋੜੇ ਬਣਾਉ ਅਤੇ ਉਹਨਾਂ ਦੇ ਹੱਲ ਜੇਕਰ ਉਸਦੀ ਹੋਂਦ ਹੋਵੇ) ਵਿਲੋਪਣ ਵਿਧੀ ਨਾਲ ਪਤਾ ਕਰੋ :
ਪ੍ਰਸ਼ਨ (i).
ਜੇਕਰ ਅਸੀਂ ਅੰਸ਼ ਵਿਚ 1 ਜੋੜ ਦੇਈਏ ਅਤੇ ਹਰ ਵਿੱਚੋਂ ਇੱਕ ਘਟਾ ਦੇਈਏ ਤਾਂ ਭਿੰਨ 1ਵਿੱਚ ਬਦਲ ਜਾਂਦੀ ਹੈ । ਜੇਕਰ ਸਿਰਫ ਹਰ ਵਿੱਚ ਜੋੜ ਦੇਈਏ ਤਾਂ ਇਹ \(\frac{1}{2}\) ਬਣ ਜਾਂਦੀ ਹੈ । ਭਿੰਨ ਪਤਾ ਕਰੋ ।
ਉੱਤਰ:
ਮੰਨ ਲਉ ਭਿੰਨ ਦਾ ਅੰਸ਼ = x
ਭਿੰਨ ਦਾ ਹਰ = y
∴ ਭਿੰਨ = \(\frac{x}{y}\)
ਪਹਿਲੀ ਸ਼ਰਤ ਅਨੁਸਾਰ
\(\frac{x+1}{y-1}\) = 1
ਜਾਂ x + 1 = y – 1
ਜਾਂ x – y + 2 = 0
ਦੂਸਰੀ ਸ਼ਰਤ ਅਨੁਸਾਰ
\(\frac{x}{y+1}\) = \(\frac{1}{2}\)
ਜਾਂ 2x = y + 1
ਜਾਂ 2x – y – 1 = 0 …..(2)
ਹੁਣ, (2) – (1) ਤੋਂ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
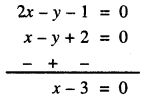
ਜਾਂ x = 3
x ਦਾ ਇਹ ਮੁੱਲ (2) ਵਿੱਚ ਪ੍ਰਤਿਸਥਾਪਿਤ ਕਰਨ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
2 × 3 – y – 1 = 0
ਜਾਂ 6 – y – 1 = 0
ਜਾਂ 5 – y = 0
ਜਾਂ y = 5
∴ ਭਿੰਨ = \(\frac{3}{5}\)
ਪ੍ਰਸ਼ਨ (ii).
ਪੰਜ ਸਾਲ ਪਹਿਲਾਂ ਨੂਰੀ ਦੀ ਉਮਰ, ਸੋਨੂੰ ਦੀ ਉਮਰ ਦਾ ਤਿੰਨ ਗੁਣਾ ਸੀ । ਦਸ ਸਾਲ ਬਾਅਦ ਨੂਰੀ ਦੀ | ਉਮਰ ,ਸੋਨੂ ਦੀ ਉਮਰ ਦਾ ਦੋ ਗੁਣਾ ਹੋ ਜਾਵੇਗੀ । ਨੂਰੀ ਅਤੇ ਸੋਨੂ ਦੀ ਉਮਰ ਕਿੰਨੀ ਹੈ ?
ਉੱਤਰ:
ਮੰਨ ਲਉ ਨੂਰੀ ਦੀ ਵਰਤਮਾਨ ਉਮਰ = x ਸਾਲ
ਸੋਨੂ ਦੀ ਵਰਤਮਾਨ ਉਮਰ = y ਸਾਲ
ਪੰਜ ਸਾਲ ਪਹਿਲਾਂ
ਨੂਰੀ ਦੀ ਉਮਰ = (x – 5) ਸਾਲ
ਸੋਨੂ ਦੀ ਉਮਰ = (y – 5) ਸਾਲ
ਪਹਿਲੀ ਸ਼ਰਤ ਅਨੁਸਾਰ
x – 5 = 3 (y – 5)
ਜਾਂ x – 5 = 3y – 15
ਜਾਂ x – 3y + 10 = 0 …(1)
ਦਸ ਸਾਲ ਬਾਅਦ
ਨੂਰੀ ਦੀ ਉਮਰ = (x + 10) ਸਾਲ
ਸੋਨੁ ਦੀ ਉਮਰ = (y + 10) ਸਾਲ
ਦੂਸਰੀ ਸ਼ਰਤ ਅਨੁਸਾਰ
x + 10 = 2 (y + 10)
ਜਾਂ x + 10 = 2y + 20
ਜਾਂ x – 2y – 10 = 0 ……(2)
ਹੁਣ (1) – (2) ਤੋਂ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ।
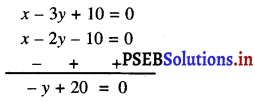
ਜਾਂ – y = – 20
ਜਾਂ y = 20
y ਦਾ ਮੁੱਲ (2) ਵਿੱਚ ਪ੍ਰਤਿਸਥਾਪਿਤ ਕਰਨ ’ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
x – 2 (20) – 0 = 0
ਜਾਂ – 40 – 10 = 0 .
ਜਾਂ x = 50
∴ ਨੂਰੀ ਦੀ ਵਰਤਮਾਨ ਉਮਰ = 50 ਸਾਲ
ਸੋਨੂ ਦੀ ਵਰਤਮਾਨ ਉਮਰ = 20 ਸਾਲ
![]()
ਪ੍ਰਸ਼ਨ (iii).
ਦੋ ਅੰਕਾਂ ਦੀ ਸੰਖਿਆ ਦੇ ਅੰਕਾਂ ਦਾ ਜੋੜ 9 ਹੈ । ਇਸ ਸੰਖਿਆ ਦਾ 9 ਗੁਣਾ, ਸੰਖਿਆ ਦੇ ਅੰਕਾਂ ਨੂੰ ਉਲਟਾ ਕੇ ਬਣੀ ਸੰਖਿਆ ਦਾ 2 ਗੁਣਾ ਹੈ । ਸੰਖਿਆ ਪਤਾ ਕਰੋ ।
ਉੱਤਰ:
ਮੰਨ ਲਉ ਇਕਾਈ ਅੰਕ = x
ਦਹਾਈ ਅੰਕ = y
∴ ਲੋੜੀਂਦੀ ਸੰਖਿਆ = 10y + x
ਪਹਿਲੀ ਸ਼ਰਤ ਅਨੁਸਾਰ
x + y = 9 ….(1)
ਉਲਟਾਉਣ ਤੇ
ਇਕਾਈ ਅੰਕ = y
ਦਹਾਈ ਅੰਕ = x
∴ ਸੰਖਿਆ = 10x + y
ਦੂਸਰੀ ਸ਼ਰਤ ਅਨੁਸਾਰ
9 [10y + x] = 2[10x + y]
ਜਾਂ 90y + 9x = 20x + 2y
ਜਾਂ 90y + 9x – 20x – 2y = 0
ਜਾਂ -11x + 88y = 0
ਜਾਂ x – 8y = 0
ਹੁਣ (2) – (1) ਤੋਂ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
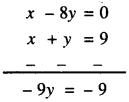
y = 1
y ਦਾ ਮੁੱਲ (2) ਵਿੱਚ ਤਿਸਥਾਪਿਤ ਕਰਨ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
x – 8 × 1 = 0
ਜਾਂ x = 8
∴ ਸੰਖਿਆ = 10y + x
= 10 × 1 + 8 = 18
ਪ੍ਰਸ਼ਨ (iv).
ਮੀਨਾ ₹2000 ਕਢਵਾਉਣ ਇੱਕ ਬੈਂਕ ਵਿੱਚ ਗਈ । ਉਸਨੇ ਖਜਾਨਚੀ ਨੂੰ ₹ 50 ਅਤੇ 100 ਦੇ ਨੋਟ ਦੇਣ ਲਈ ਕਿਹਾ | ਮੀਨਾ ਨੇ ਕੁੱਲ 2s ਨੋਟ ਪ੍ਰਾਪਤ ਕੀਤੇ । ਪਤਾ ਕਰੋ ਕਿ ਉਸਨੇ ₹ 50 ਅਤੇ ₹ 100 ਦੇ ਕਿੰਨੇ-ਕਿੰਨੇ ਨੋਟ ਪ੍ਰਾਪਤ ਕੀਤੇ ?
ਉੱਤਰ:
ਮੰਨ ਲਉ ਮੀਨਾ ਨੂੰ ਮਿਲੇ ਤੋਂ 50 ਦੇ ਨੋਟਾਂ ਦੀ ਸੰਖਿਆ = x
ਮੀਨਾ ਨੂੰ ਮਿਲੇ ਤੋਂ 100 ਦੇ ਨੋਟਾਂ ਦੀ ਸੰਖਿਆ = y
ਪਹਿਲੀ ਸ਼ਰਤ ਅਨੁਸਾਰ
x + y = 25 ……..(1)
ਦੂਸਰੀ ਸ਼ਰਤ ਅਨੁਸਾਰ
50x + 100y = 2000
ਜਾਂ x + 2y = 40 …(2)
ਹੁਣ (2) – (1) ਤੋਂ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
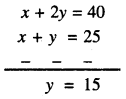
y ਦਾ ਮੁੱਲ (1) ਵਿੱਚ ਪ੍ਰਤਿਸਥਾਪਿਤ ਕਰਨ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
x + 15 = 25
ਜਾਂ x = 25 – 15 = 10
ਮੀਨਾ ਨੂੰ ਮਿਲੇ ₹ 50 ਅਤੇ ₹ 100 ਦੇ ਨੋਟਾਂ ਦੀ ਸੰਖਿਆ ਕ੍ਰਮਵਾਰ 10 ਅਤੇ 15 ਹੈ ।
![]()
ਪ੍ਰਸ਼ਨ (v).
ਕਿਰਾਏ ‘ ਤੇ ਪੁਸਤਕਾਂ ਦੇਣ ਵਾਲੀ ਕਿਸੇ ਲਾਇਬਰੇਰੀ । ਦਾ ਪਹਿਲੇ ਤਿੰਨ ਦਿਨ ਦਾ ਇੱਕ ਨਿਸ਼ਚਿਤ ਕਿਰਾਇਆ ਹੈ ਅਤੇ ਉਸ ਤੋਂ ਬਾਅਦ ਹਰ ਇੱਕ ਵਾਧੂ ਦਿਨ ਦਾ ਕਿਰਾਇਆ ਅਲੱਗ ਹੈ । ਸਰਿਤਾ ਨੇ ਸੱਤ ਦਿਨ ਤੱਕ ਇੱਕ ਪੁਸਤਕ ਰੱਖਣ ਲਈ ₹ 27 ਦਿੱਤੇ, ਜਦਕਿ ਮੰਜੂ ਨੇ ਇੱਕ ਪੁਸਤਕ ਪੰਜ ਦਿਨ ਰੱਖਣ ਲਈ ₹ 21 ਦਿੱਤੇ । ਨਿਸ਼ਚਿਤ ਕਿਰਾਇਆ ਅਤੇ ਹਰ ਇੱਕ ਵਾਧੂ ਦਿਨ ਦਾ ਕਿਰਾਇਆ ਪਤਾ ਕਰੋ ।
ਉੱਤਰ:
ਮੰਨ ਲਉ ਪਹਿਲੇ ਤਿੰਨ ਦਿਨਾਂ ਦਾ ਨਿਸ਼ਚਿਤ ਕਿਰਾਇਆ = ₹ 1
ਹਰ ਇੱਕ ਵਾਧੂ ਦਿਨ ਦਾ ਕਿਰਾਇਆ = ₹ y
ਸਰਿਤਾ ਦੀ ਸਥਿਤੀ
x + 4y = 27 ….(1)
ਮੰਜੂ ਦੀ ਸਥਿਤੀ
x + 2y = 21 ……(2)
ਹੁਣ, (1) – (2) ਤੋਂ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :

y ਦਾ ਇਹ ਮੁੱਲ (2) ਵਿੱਚ ਪ੍ਰਤਿਸਥਾਪਿਤ ਕਰਨ ਤੇ ਸਾਨੂੰ | ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
x + 2 (3) = 21
ਜਾਂ x + 6 = 21
ਜਾਂ x = 21 – 6 = 15
ਪਹਿਲੇ ਤਿੰਨ ਦਿਨਾਂ ਦਾ ਨਿਸ਼ਚਿਤ ਕਿਰਾਇਆ ਅਤੇ ਹਰੇਕ ਵਾਧੂ ਦਿਨ ਦਾ ਅਲਗ ਕਿਰਾਇਆ ਕੁਮਵਾਰ ₹ 15 ਅਤੇ ₹ 3 ਹੈ ।
