PSEB 10th Class Maths Solutions Chapter 3 ਦੋ ਚਲਾਂ ਵਿੱਚ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦੇ ਜੋੜੇ Ex 3.5

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 3 ਦੋ ਚਲਾਂ ਵਿੱਚ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦੇ ਜੋੜੇ Ex 3.5 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 10 Maths Chapter 3 ਦੋ ਚਲਾਂ ਵਿੱਚ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦੇ ਜੋੜੇ Exercise 3.5

1. ਹੇਠਾਂ ਦਿੱਤੇ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦੇ ਜੋੜੇ ਵਿੱਚੋਂ ਕਿਸ | ਦਾ ਇੱਕ ਵਿਲੱਖਣ ਹੱਲ ਹੈ, ਕਿਸ ਦਾ ਕੋਈ ਹੱਲ ਨਹੀਂ | ਜਾਂ ਕਿਸਦੇ ਅਸੀਮਿਤ ਰੂਪ ਵਿੱਚ ਅਨੇਕ ਹੱਲ ਹਨ । ਇੱਕ ਹੱਲ ਦੀ ਸਥਿਤੀ ਵਿੱਚ, ਉਸਨੂੰ ਤਿਰਛੀ ਗੁਣਾ ਦੀ ਵਿਧੀ ਨਾਲ ਪਤਾ ਕਰੋ ।

ਪ੍ਰਸ਼ਨ (i).
x – 3y – 3 = 0
3x – 9y – 2 = 0
ਉੱਤਰ:
ਦਿੱਤਾ ਗਿਆ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦਾ ਜੋੜਾ ਹੈ :
x – 3y – 3 = 0
ਅਤੇ 3x – 9y – 2 = 0
ਇੱਥੇ a₁ = 1, b₁ = -3, c₁ = – 3
a₂ = 3, b₂ = – 9, c₂ = – 2

∴ ਦਿੱਤੇ ਹੋਏ ਸਮੀਕਰਣ ਜੋੜੇ ਦਾ ਕੋਈ ਹੱਲ ਨਹੀਂ ਹੈ ।

ਪ੍ਰਸ਼ਨ (ii).
2x + y = 5
3x + 2y = 8
ਉੱਤਰ:
ਦਿੱਤਾ ਗਿਆ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦਾ ਜੋੜਾ ਹੈ :
2x + y = 5
ਅਤੇ 3x + 2y = 8
ਜਾਂ 2x + y – 5 = 0
ਅਤੇ 3x + 2y – 8 = 0
ਇੱਥੇ a₁ = 2, b₁ = 1, c₁ = -5
a₂ = 3, b₂ = 2, c₂ = – 8

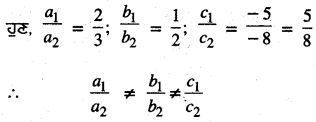
∴ ਇਸ ਲਈ ਦਿੱਤੇ ਗਏ ਸਮੀਕਰਣ ਜੋੜੇ ਦਾ ਇੱਕ ਵਿਲੱਖਣ ਹੱਲ ਹੈ

∴ x = 2 ਅਤੇ y = 1

ਪ੍ਰਸ਼ਨ (iii).
3x – 5y = 20
6r – 10y = 40
ਉੱਤਰ:
ਦਿੱਤਾ ਗਿਆ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦਾ ਜੋੜਾ ਹੈ :
3x – y = 20
ਅਤੇ 6x – 10y = 40
ਜਾਂ 3x – 5y – 20 = 0
ਅਤੇ 6 – 10y – 40 = 0
ਇੱਥੇ a₁ = 3, b₁ = -5, c₁ = – 20
a₂ = 6, b₂ = – 10, c₂ = – 40


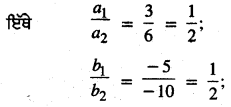
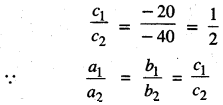
ਦਿੱਤੇ ਗਏ ਸਮੀਕਰਣ ਜੋੜੇ ਦੇ ਅਸੀਮਤ ਰੂਪ ਵਿਚ ਅਨੇਕ ਹਲ ਹਨ ।

ਪ੍ਰਸ਼ਨ (iv).
x – 3y – 7 = 0
3x – 3y – 15 = 0
ਉੱਤਰ:
ਦਿੱਤਾ ਗਿਆ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦਾ ਜੋੜਾ ਹੈ :
x – 3y – 7 = 0
ਅਤੇ 3x – 3y – 15 = 0
ਇੱਥੇ a₁ = 1, b₁ = – 3, c₁ = -7
a₂ = 3, b₂ = – 3, c₂ = – 15

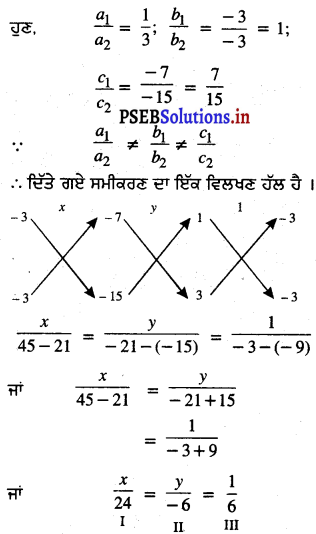
I ਅਤੇ III ਤੋਂ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
\(\frac{x}{24}\) = \(\frac{1}{6}\) ⇒ x = \(\frac{1}{6}\) × 24 = 4
II ਅਤੇ III ਤੋਂ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
\(\frac{y}{-6}\) = \(\frac{1}{6}\) ⇒ y = \(\frac{1}{6}\) × -6 = -1
ਇੱਥੇ x = 4, y = – 1

ਪ੍ਰਸ਼ਨ 2.
(i) a ਅਤੇ b ਦੇ ਕਿਹੜੇ ਮੁੱਲਾਂ ਦੇ ਲਈ, ਹੇਠਾਂ ਦਿੱਤੇ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦੇ ਜੋੜੇ ਦੇ ਅਪਰਿਮਿਤ ਰੂਪ ਵਿਚ ਅਨੇਕ ਹੱਲ ਹੋਣਗੇ ?
2x + 3y = 7
(a – b) x + (a + b) y = 3a + b – 2
ਉੱਤਰ:
ਦਿੱਤਾ ਗਿਆ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦਾ ਜੋੜਾ ਹੈ :
2 + 3y = 7
ਅਤੇ (a – b) x + (a + b) y = 3a + b – 2
ਜਾਂ 2x + 3y – 7 = 9
ਜਾਂ (a – b)x + (a + b) y – (3a + b – 2) = 0
ਇੱਥੇ a₁ = 2, b₁ = 3, c₁ = -7.
a₂ = a – b, b₂ = a + b,
c₂ = – (3a + b – 2)
∴ ਦਿੱਤੇ ਗਏ ਸਮੀਕਰਣ ਜੋੜੇ ਦੇ ਅਸੀਮਿਤ ਰੂਪ ਵਿਚ ਅਨੇਕ ਹੱਲ ਹਨ ।

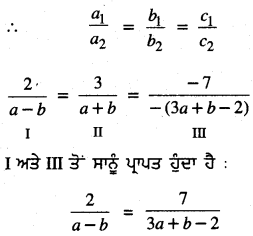
ਜਾਂ 6a + 2b – 4 = 7a – 7b
ਜਾਂ -a + 9b – 4 = 0
ਜਾਂ a = 9b – 4 ……(1)
II ਅਤੇ III ਤੋਂ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
\(\frac{3}{a+b}\) = \(\frac{7}{3a+b-2}\)
ਜਾਂ 9a + 3b – 6 = 7a + 7b
ਜਾਂ 2a – 4b – 6 = 0
ਜਾਂ a – 2b – 3 = 0 .
ਸਮੀਕਰਣ (1) ਤੋਂ a ਦਾ ਮੁੱਲ ਉਪਰੋਕਤ ਵਿਚ ਪ੍ਰਤਿਸਥਾਪਿਤ ਕਰਨ ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
ਜਾਂ 9b – 4 – 2b – 3 = 0
ਜਾਂ 7b – 7 = 0
ਜਾਂ 7b = 7
ਜਾਂ b = 1
b ਦਾ ਇਹ ਮੁੱਲ (1) ਵਿੱਚ ਪ੍ਰਤਿਸਥਾਪਿਤ ਕਰਨ ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
a = 9 × 1 – 4 = 9 – 4
a = 5
∴ a = 5 ਅਤੇ b = 1

ਪ੍ਰਸ਼ਨ (ii).
k ਦੇ ਕਿਹੜੇ ਮੁੱਲਾਂ ਲਈ, ਹੇਠਾਂ ਦਿੱਤੇ ਰੇਖੀ ਸਮੀਕਰਣ ਦੇ ਜੋੜੇ ਦਾ ਕੋਈ ਹੱਲ ਨਹੀਂ ਹੈ ?
3x + y = 1
(2k – 1) + (k – 1) y = 2 + 1
ਉੱਤਰ:
ਦਿੱਤਾ ਗਿਆ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦਾ ਜੋੜਾ ਹੈ :
3x + y = 1
ਅਤੇ 2k – 1 x + (k -11) y = 2k + 1
ਜਾਂ 3x + y – 1 = 0
ਅਤੇ (2k – 1) x + (k – 1) y – (2k + 1) = 0
ਇੱਥੇ a₁ = 3, b₁ = 1, c₁ = -1
a₂ = (2k – 1), b₂ = k – 1, c₂ = – (2k + 1)
∴ ਦਿੱਤੇ ਗਏ ਸਮੀਕਰਣ ਜੋੜੇ ਦਾ ਕੋਈ ਹੱਲ ਨਹੀਂ ਹੈ ।

⇒ 4k ≠ – 4
⇒ k ≠ \(-\frac{4}{4}\)
⇒ k ≠ -1
I ਅਤੇ II ਤੋਂ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
\(\frac{3}{2k-1}\) = \(\frac{1}{k-1}\) ⇒ 3k – 3 = 2k – 1
⇒ k = 2
∴ k = 2 ਅਤੇ k ≠ -1

ਪ੍ਰਸ਼ਨ 3.
ਹੇਠਾਂ ਦਿੱਤੇ ਰੇਖੀ ਸਮੀਕਰਣ ਜੋੜੇ ਨੂੰ ਪ੍ਰਤਿਸਥਾਪਨ ਅਤੇ ਤਿਰਛੀ ਗੁਣਾ ਵਿੱਧੀ ਨਾਲ ਹੱਲ ਕਰੋ । ਤੁਸੀਂ ਕਿਹੜੀ ਵਿਧੀ ਨੂੰ ਵੱਧ ਢੁਕਵੀਂ ਮੰਨਦੇ ਹੋ ?
8x + 5y = 9
3x + 2y = 4
ਹੱਲ:
ਦਿੱਤਾ ਗਿਆ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦਾ ਜੋੜਾ ਹੈ :
8x + 5y = 9 ……(1)
3x + 2y = 4 …(2)
ਪ੍ਰਤਿਸਥਾਪਨ ਵਿਧੀ
(2) ਤੋਂ 2y = 4 – 3x
y = \(\frac{4-3x}{2}\) …(3)
y ਦਾ ਮੁੱਲ (1), ਵਿੱਚ ਪ੍ਰਤਿਸਥਾਪਿਤ ਕਰਨ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
8x + 5[latex]\frac{4-3x}{2}[/latex] = 9
ਜਾਂ \(\frac{16x+20-15x}{2}\) = 9
ਜਾਂ x + 20 = 18
ਜਾਂ x = 18 – 20 = – 2
x ਦਾ ਇਹ ਮੁੱਲ (3) ਵਿੱਚ ਪ੍ਰਤਿਸਥਾਪਿਤ ਕਰਨ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
y = \(\frac{4-3(-2)}{2}\) = \(\frac{4+6}{2}\)
= \(\frac{10}{2}\) = 5
∴ x = – 2 ਅਤੇ y = 5
ਤਿਰਛੀ ਗੁਣਾ ਵਿਧੀ ਨਾਲ ਦਿੱਤਾ ਗਿਆ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦਾ ਜੋੜਾ ਹੈ :
8x + 5y – 9 = 0
ਅਤੇ 3x + 2y – 4 = 0
ਇੱਥੇ a₁ = 8, b₁ = 5, c₁ = – 9
a₂ = 3, b₂ = 2, c₂ = -4
ਹੁਣ, \(\frac{a_{1}}{a_{2}}\) = \(\frac{8}{3}\); \(\frac{b_{1}}{b_{2}}\) = \(\frac{5}{2}\);

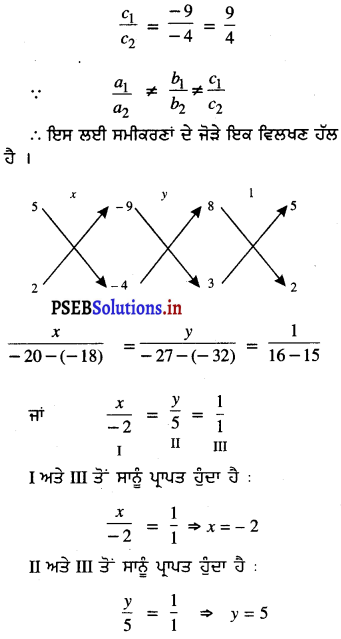
∴ x = – 2 ਅਤੇ y = 5

4. ਹੇਠਾਂ ਦਿੱਤੀਆਂ ਸਮੱਸਿਆਵਾਂ ਵਿੱਚ ਰੇਖੀ ਸਮੀਕਰਣ ਦੇ ਜੋੜੇ ਬਣਾਉ ਅਤੇ ਉਹਨਾਂ ਦੇ ਹੱਲ ਜੇਕਰ ਉਹਨਾਂ ਦੀ ਹੋਂਦ ਹੋਵੇ) ਕਿਸੇ ਵੀ ਬੀਜ ਗਣਿਤਿਕ ਵਿਧੀ ਨਾਲ ਪਤਾ ਕਰੋ :

ਪ੍ਰਸ਼ਨ (i).
ਇਕ ਹੋਸਟਲ (Hostel) ਦੇ ਮਹੀਨਾਵਾਰ ਖਰਚ ਦਾ ਇੱਕ ਭਾਗ ਨਿਸ਼ਚਿਤ ਹੈ ਅਤੇ ਬਾਕੀ ਇਸ ‘ਤੇ ਨਿਰਭਰ ਕਰਦਾ ਹੈ ਕਿ ਵਿਦਿਆਰਥੀ ਨੇ ਕਿੰਨੇ ਦਿਨ ਭੋਜਨ ਕੀਤਾ ਹੈ । ਇੱਕ ਵਿਦਿਆਰਥੀ A ਜਿਸਨੇ 20 ਦਿਨ ਭੋਜਨ ਕੀਤਾ ਹੈ, ₹ 1000 ਹੋਸਟਲ (Hostel) ਦੇ ਖਰਚ ਲਈ ਦਿੰਦਾ ਹੈ, ਜਦੋਂ ਕਿ ਦੂਸਰਾ ਵਿਦਿਆਰਥੀ B 26 ਦਿਨ ਭੋਜਨ ਕੀਤਾ ਹੈ ₹ 1180 ਖਰਚ ਦਿੰਦਾ ਹੈ । ਨਿਸ਼ਚਿਤ ਖਰਚ ਅਤੇ ਹਰ ਇੱਕ ਦਿਨ ਦੇ ਭੋਜਨ ਦਾ ਮੁੱਲ ਪਤਾ ਕਰੋ ।
ਉੱਤਰ:
ਮੰਨ ਲਉ ਹੋਸਟਲ ਦਾ ਨਿਸ਼ਚਿਤ ਮਾਸਿਕ ਕਿਰਾਇਆ = ₹ x
ਪ੍ਰਤੀਦਿਨ ਭੋਜਨ ਦਾ ਮੁੱਲ = ₹ y
ਪਹਿਲੀ ਸ਼ਰਤ ਅਨੁਸਾਰ
x + 20y = 1000
⇒ x + 26y – 1180 = 0 ………(1)
ਦੂਸਰੀ ਸ਼ਰਤ ਅਨੁਸਾਰ. .
x + 26y = 1180
⇒ x + 26y – 1180 = 0 …..(2)
ਤਿਰਛੀ ਗੁਣਾ ਵਿਧੀ ਨਾਂਲ (1) ਅਤੇ (2) ਸਮੀਕਰਣਾਂ ਨੂੰ ਹੱਲ ਕਰਨ ਲਈ ਅਸੀਂ ਹੇਠਾਂ ਦਿੱਤਾ ਚਿੱਤਰ ਬਣਾਉਂਦੇ ਹਾਂ :

ਹੋਸਟਲ ਦਾ ਨਿਸ਼ਚਿਤ ਮਾਸਿਕ ਕਿਰਾਇਆ ਅਤੇ ਪ੍ਰਤੀ ਦਿਨ ਭੋਜਨ ਦਾ ਮੁੱਲ ਕੁਮਵਾਰ ₹ 400 ਅਤੇ ₹ 30 ਹੈ

ਪ੍ਰਸ਼ਨ (ii).
ਇੱਕ ਭਿੰਨ ਦੇ ਸਿਰਫ਼ ਅੰਸ਼ ਵਿੱਚੋਂ 1 ਘਟਾਉਣ ਨਾਲ ਉਹ \(\frac{1}{3}\) ਹੋ ਜਾਂਦੀ ਹੈ ਅਤੇ ਹਰ ਵਿੱਚ 8 ਜੋੜਨ ਨਾਲ ਉਹ \(\frac{1}{4}\) ਜਾਂਦੀ ਹੈ । ਭਿੰਨ ਪਤਾ ਕਰੋ ।
ਉੱਤਰ:
ਮੰਨ ਲਉ ਭਿੰਨ ਦਾ ਅੰਸ਼ = x
ਭਿੰਨ ਦਾ ਹਰ = y
∴ ਭਿੰਨ = \(\frac{x}{y}\)
ਪਹਿਲੀ ਸ਼ਰਤ ਅਨੁਸਾਰ
\(\frac{x-1}{y}\) = \(\frac{1}{3}\)
ਜਾਂ 3x – 3 = y
ਜਾਂ 3x – y – 3 = 0 …..(1)
ਦੂਸਰੀ ਸ਼ਰਤ ਅਨੁਸਾਰ
\(\frac{x}{y+8}\) = \(\frac{1}{4}\)
ਜਾਂ 4x = y + 8
ਜਾਂ 4x – y – 8 = 0 …(2)
ਤਿਰਛੀ ਗੁਣਾ ਡਿੱਬੀ ਨਾਲ ਸਮੀਕਰਣਾਂ (1) ਅਤੇ (2) ਨੂੰ ਹੱਲ ਕਰਨ ਲਈ ਅਸੀਂ ਹੇਠਾਂ ਦਿੱਤਾ ਚਿੱਤਰ ਬਣਾਉਂਦੇ ਹਾਂ :

ਪ੍ਰਸ਼ਨ (iii).
ਯਸ਼ਪਾਲ ਨੇ ਇੱਕ ਟੈਸਟ ਵਿਚੋਂ 40 ਅੰਕ ਪ੍ਰਾਪਤ ਕੀਤੇ, ਜਦੋਂ ਉਸਨੂੰ ਸਹੀ ਉੱਤਰ ਦੇ 3 ਅੰਕ ਮਿਲੇ ਅਤੇ ਗ਼ਲਤ ਉੱਤਰ ਤੇ 1 ਅੰਕ ਦੀ ਕਟੌਤੀ ਕੀਤੀ ਗਈ । ਜੇਕਰ ਉਸ ਨੂੰ ਸਹੀ ਉੱਤਰ ਦੇ 4 ਅੰਕ ਮਿਲਣ ਅਤੇ ਗ਼ਲਤ ਉੱਤਰ ਦੇ 2 ਅੰਕ ਕਟੇ ਜਾਣ ਤਾਂ ਉਹ 50 ਅੰਕ ਪ੍ਰਾਪਤ ਕਰਦਾ ਹੈ । ਟੈਸਟ ਵਿਚ ਕਿੰਨੇ ਪ੍ਰਸ਼ਨ ਸਨ ?
ਉੱਤਰ:
ਮੰਨ ਲਉ ਯਸ਼ਪਾਲ ਦੁਆਰਾ ਕੀਤੇ ਸਹੀ ਪ੍ਰਸ਼ਨ = x
ਯਸ਼ਪਾਲ ਦੁਆਰਾ ਕੀਤੇ ਗ਼ਲਤ ਪ੍ਰਸ਼ਨ = y
ਪਹਿਲੀ ਸ਼ਰਤ ਅਨੁਸਾਰ
3x – y = 40
ਜਾਂ 3x – y – 40 = 0 …….(1)
ਦੂਜੀ ਸ਼ਰਤ ਅਨੁਸਾਰ
4x – 2y = 50
ਜਾਂ 4x – 2y – 50 = 0 …(2)
ਤਿਰਛੀ ਗੁਣਾ ਵਿਧੀ ਨਾਲ ਸਮੀਕਰਣਾਂ (1) ਅਤੇ (2) ਨੂੰ ਹੱਲ ਕਰਨ ਲਈ ਅਸੀਂ ਹੇਠਾਂ ਦਿੱਤਾ ਚਿੱਤਰ ਬਣਾਉਂਦੇ ਹਾਂ :


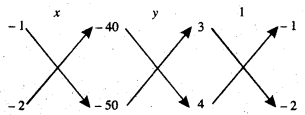
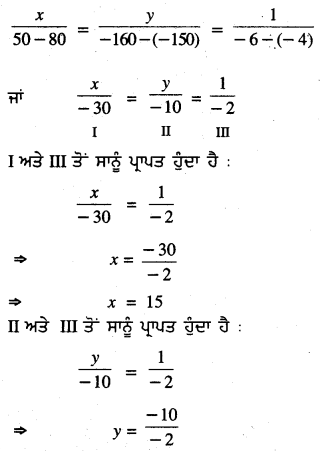
⇒ y = 5
∴ ਸਹੀ ਪ੍ਰਸ਼ਨਾਂ ਦੀ ਗਿਣਤੀ = 15
ਗ਼ਲਤ ਪ੍ਰਸ਼ਨਾਂ ਦੀ ਗਿਣਤੀ = 5
ਕੁਲ ਪ੍ਰਸ਼ਨ = ਸਹੀ ਪ੍ਰਸ਼ਨ + ਗ਼ਲਤ ਪ੍ਰਸ਼ਨ
=15 + 5 = 20

ਪ੍ਰਸ਼ਨ (iv).
ਇੱਕ ਰਾਜਮਾਰਗ ‘ਤੇ ਦੋ ਸਥਾਨ A ਅਤੇ B, 100 ਕਿ.ਮੀ. ਦੀ ਦੂਰੀ ‘ਤੇ ਹਨ । ਇਕ ਕਾਰ A ਤੋਂ ਅਤੇ ਦੂਸਰੀ ਕਾਰ B ਤੋਂ ਇੱਕੋ ਤੋਂ ਹੀ ਸਮੇਂ ‘ਤੇ ਚਲਣਾ ਸ਼ੁਰੂ ਕਰਦੀਆਂ ਹਨ । ਜੇਕਰ ਇਹ ਕਾਰਾਂ ਅਲੱਗ-ਅਲੱਗ ਚਾਲ ਗਤੀ ਨਾਲ ਇੱਕ ਹੀ ਦਿਸ਼ਾ ਵਿੱਚ ਚਲਦੀਆਂ ਹਨ, ਤਾਂ ਇਹ 5 ਘੰਟੇ ਬਾਅਦ ਮਿਲ ਜਾਣਗੀਆਂ | ਦੋਵਾਂ ਕਾਰਾਂ ਦੀ ਗਤੀ (ਚਾਲ) ਪਤਾ ਕਰੋ ।
ਉੱਤਰ:
ਮੰਨ ਲਉ ਸਥਾਨ A ਵਾਲੀ ਕਾਰ ਦੀ ਚਾਲ = 1 ਕਿ.ਮੀ. /ਘੰਟਾ
ਅਤੇ ਸਥਾਨ B ਵਾਲੀ ਕਾਰ ਦੀ ਚਾਲ = y ਕਿ.ਮੀ. /ਘੰਟਾ
A ਅਤੇ B ਵਿਚਕਾਰਲੀ ਦੂਰੀ = 100 ਕਿ.ਮੀ.
5 ਘੰਟੇ ਦੀ ਸਥਿਤੀ ਵਿਚ
ਕਾਰ A ਦੁਆਰਾ ਤੈਅ ਕੀਤੀ ਗਈ ਦੂਰੀ = 5 ਕਿ.ਮੀ.
[∵ ਦੂਰੀ = ਚਾਲ × ਸਮਾਂ]
ਕਾਰ B ਦੁਆਰਾ ਤੈਅ ਕੀਤੀ ਗਈ ਦੂਰੀ = 5y ਕਿ.ਮੀ.
ਪਹਿਲੀ ਸ਼ਰਤ ਅਨੁਸਾਰ
5x – 5y = 100
ਜਾਂ x – y = 20
ਜਾਂ x – y – 20 = 0 …..(1)
ਇੱਕ ਘੰਟੇ ਦੀ ਸਥਿਤੀ ਵਿੱਚ
ਕਾਰ ਦੁਆਰਾ ਤੈਅ ਕੀਤੀ ਗਈ ਦੂਰੀ = 1 ਕਿ.ਮੀ.
[∵ ਦੂਰੀ = ਚਾਲ × ਸਮਾਂ]
ਕਾਰ B ਦੁਆਰਾ ਤੈਅ ਕੀਤੀ ਦੂਰੀ = y ਕਿ.ਮੀ.
ਦੂਸਰੀ ਸ਼ਰਤ ਅਨੁਸਾਰ
x + y = 10 ,
ਜਾਂ x + y – 100 = 00 …..(2)
ਤਿਰਛੀ ਗੁਣਾ ਵਿੱਧੀ ਨਾਲ ਸਮੀਕਰਣ (1) ਅਤੇ (2) ਨੂੰ ਹੱਲ ਕਰਨ ਲਈ ਅਸੀਂ ਹੇਠਾਂ ਦਿੱਤਾ ਚਿੱਤਰ ਬਣਾਉਂਦੇ ਹਾਂ :

ਬਿੰਦੂ A ਅਤੇ B ਤੋਂ ਚੱਲਣ ਵਾਲੀ ਕਾਰਾਂ ਦੀ ਚਾਲ ਕ੍ਰਮਵਾਰ 60 ਕਿ.ਮੀ./ਘੰਟਾ ਅਤੇ 40 ਕਿ.ਮੀ. /ਘੰਟਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ (v).
ਜੇਕਰ ਇੱਕ ਆਇਤ ਦੀ ਲੰਬਾਈ ਨੂੰ 5 ਇਕਾਈਆਂ ਘਟਾ ਦੇਈਏ ਅਤੇ ਚੌੜਾਈ ਨੂੰ 3 ਇਕਾਈਆਂ ਵਧਾ ਦੇਈਏ ਤਾਂ ਆਇਤ ਦਾ ਖੇਤਰਫਲ 9 ਵਰਗ ਇਕਾਈਆਂ ਘੱਟ ਜਾਂਦਾ ਹੈ । ਜੇਕਰ ਅਸੀਂ ਲੰਬਾਈ । 6 ਇਕਾਈਆਂ ਅਤੇ ਚੌੜਾਈ ਨੂੰ 2 ਇਕਾਈਆਂ ਵਧਾ ਦੇਈਏ ਤਾਂ ਖੇਤਰਫਲ 67 ਵਰਗ ਇਕਾਈਆਂ ਵੱਧ ਜਾਂਦਾ ਹੈ । ਆਇਤ ਦੀ ਲੰਬਾਈ ਅਤੇ ਚੌੜਾਈ ਪਤਾ ਕਰੋ ।
ਉੱਤਰ:
ਮੰਨ ਲਉ ਆਇਤ ਦੀ ਲੰਬਾਈ = x ਇਕਾਈਆਂ
ਆਇਤ ਦੀ ਚੌੜਾਈ = y ਇਕਾਈਆਂ
∴ ਆਇਤ ਦਾ ਖੇਤਰਫਲ = xy ਵਰਗ ਇਕਾਈਆਂ
ਪਹਿਲੀ ਸ਼ਰਤ ਅਨੁਸਾਰ
(x – 5) (y + 3) = xy – 9
ਜਾਂ xy + 3x – 5y – 15 = xy – 9
ਜਾਂ 3x – 5y – 6 = 0 ….(1)
ਦੂਸਰੀ ਸ਼ਰਤ ਅਨੁਸਾਰ
(x + 3) (y + 2) = xy + 67
ਜਾਂ xy + 2x + 3y + 6 = xy + 67
ਜਾਂ 2x + 35 – 61 = 0 …(2)
ਤਿਰਛੀ ਗੁਣਾ ਵਿਧੀ ਨਾਲ ਸਮੀਕਰਣਾਂ (1) ਅਤੇ (2) ਨੂੰ ਕੱਲ ਕਰਨ ਲਈ ਅਸੀਂ ਹੇਠਾਂ ਦਿੱਤਾ ਚਿੱਤਰ ਬਣਾਉਂਦੇ ਹਾਂ,

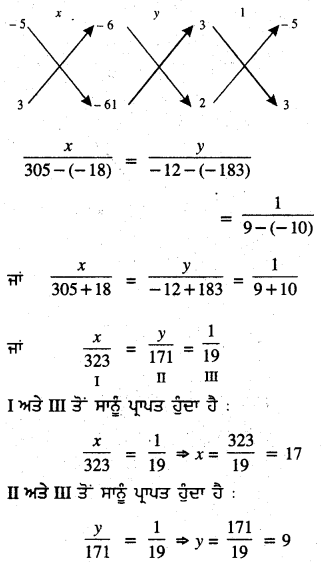
ਆਇਤ ਦੀ ਲੰਬਾਈ ਅਤੇ ਚੌੜਾਈ ਕ੍ਰਮਵਾਰ 17 ਇਕਾਈਆਂ ਅਤੇ 9 ਇਕਾਈਆਂ ਹੈ ।