PSEB 10th Class Maths Solutions Chapter 3 दो चर वाले रैखिक समीकरण युग्म Ex 3.6

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 3 दो चर वाले रैखिक समीकरण युग्म Ex 3.6 Textbook Exercise Questions and Answers

PSEB Solutions for Class 10 Maths Chapter 3 दो चर वाले रैखिक समीकरण युग्म Ex 3.6

प्रश्न 1.
निम्न समीकरणों के युग्मों को रैखिक समीकरण युग्म में बदल करके हल कीजिए :
(i) \(\frac{1}{2 x}+\frac{1}{3 y}\) = 2

\(\frac{1}{3 x}+\frac{1}{2 y}=\frac{13}{6}\)

(ii) \(\frac{2}{\sqrt{x}}+\frac{3}{\sqrt{y}}\) = 2

\(\frac{4}{\sqrt{x}}-\frac{9}{\sqrt{y}}\) = – 1

(iii) \(\frac{4}{x}\) + 3y = 14
\(\frac{3}{x}\) – 4y = 23

(iv) \(\frac{5}{x-1}+\frac{1}{y-2}\) = 2

\(\frac{6}{x-1}-\frac{3}{y-2}\) = 1

(v) \(\frac{7 x-2 y}{x y}\) = 5

\(\frac{8 x+7 y}{x y}\) = 15

(vi) 6x + 3y = 6xy
2x + 4y = 5xy

(vii) \(\frac{10}{x+y}+\frac{2}{x-y}\) = 4

\(\frac{15}{x+y}-\frac{5}{x-y}\) = – 2

(viii) \(\frac{1}{3 x+y}+\frac{1}{3 x-y}=\frac{3}{4}\)

\(\frac{1}{2(3 x+y)}-\frac{1}{2(3 x-y)}=\frac{-1}{8}/latex]

हल :
(i) दिया गया रैखिक समीकरण युग्म हैं :
[latex]\frac{1}{2 x}+\frac{1}{3 y}\) = 2
और \(\frac{1}{3 x}+\frac{1}{2 y}=\frac{13}{6}\)

\(\frac{1}{x}\) = u और \(\frac{1}{y}\) = v,
प्रतिस्थापित करने पर
\(\frac{u}{2}+\frac{v}{3}\) = 2

या \(\frac{3 u+2 v}{6}\) = 2

3u + 2v = 12 ……………(1)

और \(\frac{u}{3}+\frac{v}{2}=\frac{13}{6}\)

या \(\frac{2 u+3 v}{6}=\frac{13}{6}\)

या 2u + 3v = 13 ………(2)
(1) को 2 से और (2) को 3 से, गुणा करने पर हमें प्राप्त होता है:
6u + 4y = 24 ……………(3)
और 6u + 9y = 39 ……………(4)
अब, (4) – (3) से प्राप्त होता है,

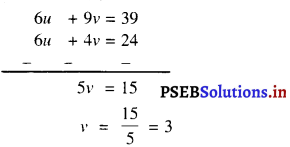
v के इस मान को (1) में प्रतिस्थापित करने पर, हमें प्राप्त होता है :
3u + 2 (3) = 12
या 3u + 6 = 12
3u = 12 – 6 = 6
या u = \(\frac{6}{3}\) = 2

\(\frac{1}{x}\) = u

या x = \(\frac{1}{u}\)

या x = \(\frac{1}{2}\)

और \(\frac{1}{y}\) = v

या y = \(\frac{1}{v}\)

या y = \(\frac{1}{3}\)
अतः, x = \(\frac{1}{2}\) और y = \(\frac{1}{3}\).

(ii) दिया गया रैखिक समीकरण युग्म है :
\(\frac{2}{\sqrt{x}}+\frac{3}{\sqrt{y}}\) = 2 और \(\frac{4}{\sqrt{x}}-\frac{9}{\sqrt{y}}\) = – 1

\(\frac{1}{\sqrt{x}}\) = u और \(\frac{1}{\sqrt{y}}\) = v
प्रतिस्थापित करने पर
2u + 3v = 2 ……………(1)
और 4u – 9v = – 1 ………….(2)
(1) को 2 से गुणा करने पर हमें प्राप्त होता है।
4u + 6v = 4 …………….(3)
अब, (2) – (3) से प्राप्त होता है :

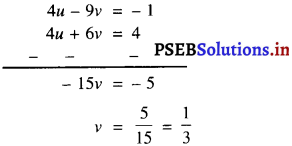
v के इस मान को (1) में प्रतिस्थापित करने पर हमें प्राप्त होता है :
2u + 3(\(\frac{1}{3}\)) = 2
या 2u + 1 = 2
या 2u = 2 – 1 = 1
या u = \(\frac{1}{2}\)

परंतु \(\frac{1}{\sqrt{x}}\) = u²

या \(\left(\frac{1}{\sqrt{x}}\right)^{2}\) = u²

या \(\frac{1}{x}\) = u²

या \(\frac{1}{x}=\left(\frac{1}{2}\right)^{2}\)

या x = 4

और \(\frac{1}{\sqrt{y}}\) = v

या \(\left(\frac{1}{\sqrt{y}}\right)^{2}\) = v²

या \(\frac{1}{y}\) = v²

या \(\frac{1}{y}=\left(\frac{1}{3}\right)^{2}\)

अतः, x = 4 और y = 9.

(iii) दिया गया रैखिक समीकरण युग्म है :
\(\frac{4}{x}\) + 3y = 14 और \(\frac{3}{x}\) – 4y = 23

\(\frac{1}{x}\) = v रखने पर

4v + 3y = 14 ………….(1)
और 3v – 4y = 23 …………..(2)
(1) को 3 से और (2) को 4 से गुणा करने पर हमें प्राप्त होता है :
12v + 9y = 42 ……………..(3)
और 12v – 16y = 92 ………..(4)
अब, (4) – (3) से प्राप्त होता है :

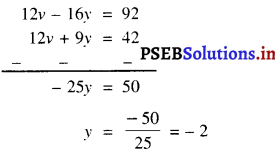
y के इस मान को (1) में प्रतिस्थापित करने पर हमें प्राप्त होता है :
4v + 3 (- 2) = 14
या 4v – 6 = 14
या 4v = 14 + 6 = 20
या v = \(\frac{20}{4}\) = 5

परंतु \(\frac{1}{x}\) = v,

या x = \(\frac{1}{v}=\frac{1}{5}\)

अतः, x = = और y = – 2.

(iv) दिया गया रैखिक समीकरण युग्म है :
\(\frac{5}{x-1}+\frac{1}{y-2}\) = 2 और \(\frac{6}{x-1}-\frac{3}{y-2}\) = 1

\(\frac{1}{x-1}\) = u और \(\frac{1}{y-2}\) = v रखने पर प्राप्त समीकरण है :
5u + y = 2 ………….(1)
6u – 3v = 1 ………….(2)
(1) का 3 स गुणा करन पर हम प्राप्त होता है :
15u + 3y = 6 …………..(3)
अब, (3) + (2) से प्राप्त होता है

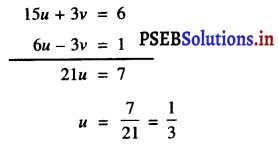
u के इस मान को (1) में प्रतिस्थापित करने पर हमें प्राप्त होता है :
5 × \(\frac{1}{3}\) + v = 2
या v = 2 – \(\frac{5}{3}\) = \(\frac{6-5}{3}\)

v = \(\frac{1}{3}\)

परंतु \(\frac{1}{x-1}\) = u

\(\frac{1}{x-1}=\frac{1}{3}\)

या x – 1 = 3
या x= 3 + 1
या x = 4

\(\frac{1}{y-2}\) = v

\(\frac{1}{y-2}=\frac{1}{3}\)
या y – 2 = 3
या y = 3 + 2
या y = 5
अतः, x = 4 और y = 5.

(v) दिया गया रैखिक समीकरण युग्म है :

\(\frac{1}{x}\) = u और \(\frac{1}{y}\) = v, रखने पर प्राप्त समीकरण है :
– 2u + 7v = 5 …………..(1)
और 7u + 8y = 15 ………….(2)
(1) को 7 से और (2) को 2 से गुणा करने पर, हमें प्राप्त होता है :
– 14y + 49u = 35 …………….(3)
और 14v + 16u = 30 …………….(4)
अब, (3) + (4) से प्राप्त होता है :

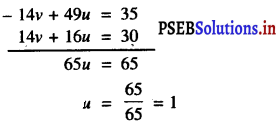
u के इस मान को (1) में प्रतिस्थापित करने पर
– 2 (1) + 7v = 5
7v = 5 + 2
7v = 7
v = \(\frac{7}{7}\) = 1
या y = 1
अतः x = 1 और y = 1

(vi) दिया गया रैखिक समीकरण युग्म है :

\(\frac{1}{x}\) = u और \(\frac{1}{y}\) = v, प्रतिस्थापित करने पर हमें प्राप्त होता है :
u + 2v = 2 …………(1)
और 4u + 2y = 5 ………….(2)
अब, (2) – (1) से प्राप्त होता है

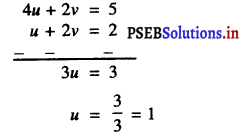
u के इस मान को (1) में प्रतिस्थापित करने पर हमें | प्राप्त होता है :
1 + 2v = 2
या 2v = 2 – 1 = 1
या v = \(\frac{1}{2}\)

परंतु \(\frac{1}{x}\) = u

या \(\frac{1}{x}\) = 1

या x = 1

और \(\frac{1}{y}\) = v

या \(\frac{1}{y}\) = \(\frac{1}{2}\)

या y = 2
अतः, x = 1 और y = 2.

(vii) दिया गया रैखिक समीकरण युग्म है :
\(\frac{10}{x+y}+\frac{2}{x-y}\) = 4

और \(\frac{15}{x+y}-\frac{5}{x-y}\) = – 2

\(\frac{1}{x+y}\) = u और \(\frac{1}{x-y}\) = v को प्रतिस्थापित करने पर :
10u + 2v = 4
या 5u + y = 2 ………….(1)
15u -5v=-2 …………..(2)
(1) को 5 से गुणा करने पर हमें प्राप्त होता है
25u + 5v = 10 …………(3)

अब, (3) + (2) से प्राप्त होता है :

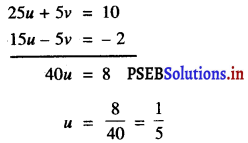
u को (1) में प्रतिस्थापित करने पर हमें प्राप्त होता
5(\(\frac{1}{5}\)) + v = 2
या 1 + v = 2
या v = 2 – 1 = 1
परंतु \(\frac{1}{x+y}\) = u

\(\frac{1}{x+y}=\frac{1}{5}\)
या x + y =5 …………(4)

और \(\frac{1}{x-y}\) = v

या \(\frac{1}{x – y}\) = 1
या x – y = 1 ………..(5)
अब, (4) + (5) से प्राप्त होता है :

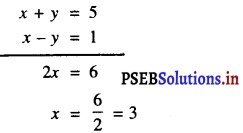
x के इस मान को (4) में प्रतिस्थापित करने पर हमें प्राप्त होता है :
3 + y = 5
y = 5 – 3 = 2
अतः x = 3 और y = 2

(viii) दिया गया रैखिक समीकरण युग्म है :
\(\frac{1}{3 x+y}+\frac{1}{3 x-y}=\frac{3}{4}\)

और \(\frac{1}{2(3 x+y)}-\frac{1}{2(3 x-y)}=\frac{-1}{8}\)

\(\frac{1}{3 x+y}\) = u \(\frac{1}{3 x-y}\) = v को रखने पर

u + v = \(\frac{3}{4}\)

या 4u + 4y = 3
या 4u + 4v = 3 …………..(1)

और \(\frac{u}{2}-\frac{v}{2}=\frac{-1}{8}\)

या 4u – 4v = \(\frac{-1}{4}\)

या 4u – 4v = – 1
अब, (1) + (2) से प्राप्त होता है

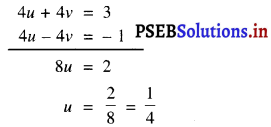
u के इस मान को (1) में प्रतिस्थापित करने पर हमें प्राप्त होता है :
4(\(\frac{1}{4}\)) + 4v = 3
या 4v = 2
या v = \(\frac{2}{4}=\frac{1}{2}\)

परंतु \(\frac{1}{3 x+y}\)

या 3x + y = 4 ………….(3)

और \(\frac{1}{3 x-y}=\frac{1}{2}\)
या 3x – y = 2 ………..(4)
अब, (3) + (4) से प्राप्त होता है :

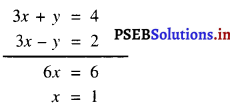
x के इस मान को (3) में प्रतिस्थापित करने पर हमें प्राप्त होता है :
3 (1) + y = 4
या 3 + y = 4
या y = 4 – 3 = 1
अतः x = 1 और y = 1.

प्रश्न 2.
निम्न समस्याओं को रैखिक समीकरण युग्म के रूप में व्यक्त कीजिए और फिर उनके हल ज्ञात कीजिए :
(i) रितु धारा के अनुकूल 2 घंटे में 20 km तैर सकती है और धारा के प्रतिकूल 2 घंटे में 4 km तैर सकती है। उसकी स्थिर जल में तैरने की चाल तथा धारा की चाल ज्ञात कीजिए।

(ii) 2 महिलाएँ एवं 5 पुरुष एक कसीदे के काम को साथ-साथ 4 दिन में पूरा कर सकते हैं, जबकि 3 महिलाएँ एवं 6 पुरुष इसको 3 दिन में पूरा कर सकते हैं। ज्ञात कीजिए कि इसी कार्य को करने में एक अकेली महिला कितना समय लेगी ? पुनः इसी कार्य को करने में एक पुरुष कितना समय लेगा ?

(iii) रूही 300 km दूरी पर स्थित अपने घर जाने के लिए कुछ दूरी रेलगाड़ी द्वारा तथा कुछ दूरी बस द्वारा तय करती है। यदि वह 60 km रेलगाड़ी द्वारा तथा शेष बस द्वारा यात्रा करती है तो उसे 4 घंटे लगते हैं। यदि वह 100 km रेलगाड़ी से तथा शेष बस से यात्रा करे, तो उसे 10 मिनट अधिक लगते हैं । रेलगाड़ी एवं बस की क्रमशः चाल ज्ञात कीजिए।
हल :
(i) मान लीजिए स्थिर जल में रितु की चाल = x किमी/घंटा
और धारा की चाल = 1 किमी/घंटा
∴ धारा के प्रतिकूल चाल = (x – 1) किमी/घंटा
और धारा के अनुकूल चाल = (x + 1) किमी/घंटा
रीतु द्वारा धारा के अनुकूल में 2 घंटे में तय की गई दूरी = चाल × समय
= (x + 3) × 2
किमी पहली शर्त अनुसार,
2 (x + y) = 20
x + y = 10 …………(1)
रितु द्वारा धारा के प्रतिकूल 2 घंटे में तय की गई दूरी = चाल × समय
= 2 (x – y) किमी
दूसरी शर्त अनुसार,
2 (x – y) = 4
x – y = 2 ……………(2)
अब, (1) + (2) से प्राप्त होता है :
x + y = 10
x – y = 2
2x = 12
x = \(\frac{12}{2}\) = 6
x के इस मान को (1) में भरने पर हमें प्राप्त होता है :
6 + y = 10
y = 10 – 6 = 4
अतः, रितु की स्थिर जल में चाल = 6 किमी/घंटा
और धारा की चाल = 4 किमी/घंटा

(ii) मान लीजिए एक महिला काम समाप्त कर सकती है = x दिन में
एक पुरुष काम को समाप्त कर सकता है = y दिन में
तब, एक महिला का 1 दिन का काम = \(\frac{1}{x}\)

एक महिला का 1 दिन का काम = \(\frac{1}{y}\)
पहली शर्त अनुसार,

\(\frac{2}{x}+\frac{5}{y}=\frac{1}{4}\) ………(1)

दूसरी शर्त अनुसार

\(\frac{3}{x}+\frac{6}{y}=\frac{1}{3}\) ……….(2)

\(\frac{1}{x}\) = u और \(\frac{1}{y}\) = v रखने पर, समीकरणे (1) और (2) बन जाती हैं :

2u + 5v = \(\frac{1}{4}\)

8u + 20v = 1 …………..(3)

और 3u + 6v = \(\frac{1}{3}\)

9u + 18y = 1 …………..(4)
(3) को 9 से और (4) को 8 से गुणा करने पर हमें प्राप्त होता है।
72u + 180v = 9 ……………(5)
और 72u + 144v = 8 ……………..(6)
तब, (5)- (6) से प्राप्त होता है :

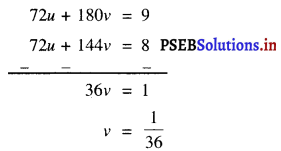
v के इस मान को (4) में प्रतिस्थापित करने पर, हमें प्राप्त होता है :
9u + 18(\(\frac{1}{36}\)) = 1

या 9u + \(\frac{1}{2}\) = 1

या 9u = 1 – \(\frac{1}{2}\)
= \(\frac{2-1}{2}\)

या 9u = \(\frac{1}{2}\)

या 9u = \(\frac{1}{2}\)

या u = \(\frac{1}{2 \times 9}=\frac{1}{18}\)

परंतु \(\frac{1}{x}\) = u

या \(\frac{1}{x}=\frac{1}{18}\)

या x = 18

और \(\frac{1}{y}\) = v

या \(\frac{1}{y}=\frac{1}{36}\)

या y = 36
अतः, एक महिला और एक पुरुष अकेले-अकेले काम को क्रमश: 18 दिन और 36 दिन में पूरा कर सकते हैं।

(iii) मान लीजिए रेल गाड़ी की चाल = x किमी/घंटा और
बस की चाल = y किमी/घंटा
कुल दूरी = 300 किमी

स्थिति I:
60 किमी दूरी तय करने में लिया गया समय = दूरी / चाल
= \(\frac{60}{x}\) घंटे

बस द्वारा 240 (= 300 – 60) किमी दूरी तय करने में लिया गया समय = 240/y घंटे
∴ कुल समय = \(\) घंटे
पहली शर्त अनुसार
\(\frac{60}{x}+\frac{240}{y}\) = 4

या \(\frac{15}{x}+\frac{60}{y}\) = 1 ………….(1)

स्थिति II:
रेलगाड़ी द्वारा 100 किमी दूरी तय करने में लगा समय = 100/x घंटे
बस द्वारा 200 (= 300 – 100) किमी दूरी तय करने में लिया गया समय = 200 / y घंटे

\(\frac{1}{x}\) = u और \(\frac{1}{y}\) = y को समीकरणों
(1) और (2) में रखने पर प्राप्त समीकरण हैं :
15u + 60v = 1
और 24u + 48v = 1

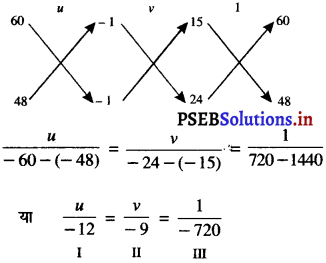
I और III से हमें प्राप्त होता है :

\(\frac{u}{-12}=\frac{1}{-720}\)

u = \(\frac{12}{720}=\frac{1}{60}\)

II और III से हमें प्राप्त होता है :
\(\frac{v}{-9}=\frac{1}{-720}\)

v = \(\frac{9}{720}=\frac{1}{80}\)

परंतु \(\frac{1}{x}\) = u

या \(\frac{1}{x}=\frac{1}{60}\)

या x = 60

\(\frac{1}{y}\) = v

या \(\frac{1}{y}=\frac{1}{60}\)

या y = 80
अतः, रेल गाड़ी की और बस की चाल क्रमश: 60 किमी/घंटा और 80 किमी/घंटा है।xzc