Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 3 ਦੋ ਚਲਾਂ ਵਿੱਚ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦੇ ਜੋੜੇ Ex 3.6 Textbook Exercise Questions and Answers.
PSEB Solutions for Class 10 Maths Chapter 3 ਦੋ ਚਲਾਂ ਵਿੱਚ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦੇ ਜੋੜੇ Exercise 3.6
1. ਹੇਠਾਂ ਦਿੱਤੇ ਸਮੀਕਰਣ ਜੋੜਿਆਂ ਨੂੰ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦੇ ਵਿੱਚ ਬਦਲ ਕੇ ਹੱਲ ਕਰੋ :
ਪ੍ਰਸ਼ਨ (i).
\(\frac{1}{2x}\) + \(\frac{1}{3y}\) = 2
\(\frac{1}{3x}\) + \(\frac{1}{2y}\) = \(\frac{13}{6}\)
ਉੱਤਰ:
ਦਿੱਤਾ ਗਿਆ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦਾ ਜੋੜਾ ਹੈ
\(\frac{1}{2x}\) + \(\frac{1}{3y}\) = 2
ਮਤੇ \(\frac{1}{3x}\) + \(\frac{1}{2y}\) = \(\frac{13}{6}\)
\(\frac{1}{x}\) = u, \(\frac{1}{v}\) = v ਮਤੇ ਤਿਸਥਾਪਿਤ ਕਰਨ ‘ਤੇ

(1) ਨੂੰ 2 ਨਾਲ ਅਤੇ (2) ਨੂੰ 3 ਨਾਲ ਗੁਣਾ ਕਰਨ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
6u + 4v = 24 …(3)
ਅਤੇ 6u + 9v = 39 …(4)
ਹੁਣ, (4) – (3) ਤੋਂ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
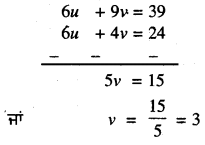
v ਦੇ ਇਸ ਮੁੱਲ ਨੂੰ (1) ਵਿਚ ਤਿਸਥਾਪਿਤ ਕਰਨ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
3u + 2 (3) = 12
ਜਾਂ 3u + 6 = 12
ਜਾਂ 3u = 12 – 6 = 6
ਜਾਂ u = \(\frac{6}{3}\) = 2
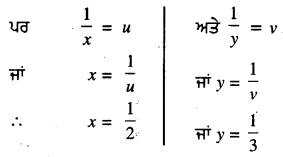
x = \(\frac{1}{2}\) ਮਤੇ y = \(\frac{1}{3}\)
ਪ੍ਰਸ਼ਨ (ii).
\(\frac{2}{\sqrt{x}}\) + \(\frac{3}{\sqrt{y}}\) = 2
\(\frac{4}{\sqrt{x}}\) – \(\frac{9}{\sqrt{y}}\) = -1
ਉੱਤਰ:
ਦਿੱਤਾ ਗਿਆ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦਾ ਜੋੜਾ ਹੈ :
\(\frac{2}{\sqrt{x}}\) + \(\frac{3}{\sqrt{y}}\) = 2 ਅਤੇ \(\frac{4}{\sqrt{x}}\) – \(\frac{9}{\sqrt{y}}\) = -1
\(\frac{1}{\sqrt{x}}\) = u ਅਤੇ \(\frac{1}{\sqrt{y}}\) = v ਤਿਸਥਾਪਿਤ ਕਰਨ ‘ਤੇ
2u + 3v = 2 ….(1)
ਅਤੇ 4u – 9y = – 1 …(2)
(1) ਨੂੰ 2 ਨਾਲ ਗੁਣਾ ਕਰਨ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
4u + 6v = 4 …(3)
ਹੁਣ (2) – (3) ਤੋਂ ਸਾਨੂੰ ਮਿਲਦਾ ਹੈ ।
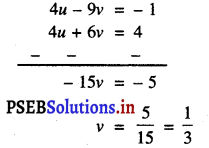
v ਦਾ ਇਹ ਮੁੱਲ (1) ਵਿਚ ਤਿਸਥਾਪਿਤ ਕਰਨ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
2u + 3\(\left(\frac{1}{3}\right)\) = 2
ਜਾਂ 2u + 1 = 2
ਜਾਂ 2u = 2 – 1 = 1
ਜਾਂ u = \(\frac{1}{2}\)
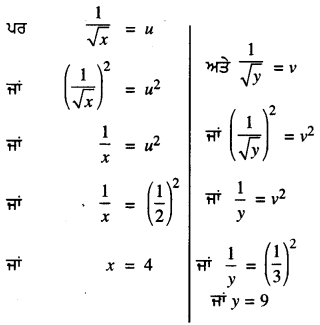
x = 4 ਅਤੇ y = 9
![]()
ਪ੍ਰਸ਼ਨ (iii).
\(\frac{4}{x}\) + 3y = 14
\(\frac{3}{x}\) – 4y = 23
ਉੱਤਰ:
ਦਿੱਤਾ ਗਿਆ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦਾ ਜੋੜਾ ਹੈ :
\(\frac{4}{x}\) + 3y = 14 ਅਤੇ \(\frac{3}{x}\) – 4y = 23
\(\frac{1}{x}\) = v ਤਿਸਥਾਪਿਤ ਕਰਨ ‘ਤੇ
4v + 3y = 14 …(1)
ਅਤੇ 3v – 4y = 23 …(2)
(1) ਨੂੰ 3 ਨਾਲ (2) ਨੂੰ 4 ਨਾਲ ਗੁਣਾ ਕਰਨ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
12v + 9y = 42 ….(3)
ਅਤੇ 12v – 16y = 92 …..(4)
ਹੁਣ, (4) – (3) ਤੋਂ

y ਦਾ ਮੁੱਲ (1) ਵਿੱਚ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
ਜਾਂ 4v + 3 (-2) = 14
ਜਾਂ 4v – 6 = 14
ਜਾਂ 4v = 14 + 6 = 20
ਪਰ \(\frac{1}{x}\) = v
ਜਾਂ x = \(\frac{1}{v}\) = \(\frac{1}{5}\)
x = \(\frac{1}{5}\) ਅਤੇ y = – 2
ਪ੍ਰਸ਼ਨ (iv).
\(\frac{5}{x-1}\) + \(\frac{1}{y-2}\) = 2
\(\frac{6}{x-1}\) – \(\frac{3}{y-2}\) = 1
ਉੱਤਰ:
ਦਿੱਤਾ ਗਿਆ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦਾ ਜੋੜਾ ਹੈ :
\(\frac{5}{x-1}\) + \(\frac{1}{y-2}\) = 2 ਅਤੇ \(\frac{6}{x-1}\) – \(\frac{3}{y-1}\) = 1
\(\frac{1}{x-1}\) = u ਅਤੇ \(\frac{1}{y-2}\) = v ਤਿਸਥਾਪਿਤ ਕਰਨ ‘ਤੇ
5u + v = 2 …(1)
ਅਤੇ 6u – 3v = 1 …(2)
(1) ਨੂੰ 3 ਤੇ ਗੁਣਾ ਕਰਨ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
15u + 3v = 6 …….3)
ਹੁਣ, (3) + (2) ਤੋਂ ਸਾਨੂੰ ਮਿਲਦਾ ਹੈ ।
15u + 3v = 6
6u – 3v = 1
21u = 7
u = \(\frac{7}{21}\) = \(\frac{1}{3}\)
u ਦੇ ਮੁੱਲ ਨੂੰ (1) ਵਿੱਚ ਪ੍ਰਤਿਸਥਾਪਿਤ ਕਰਨ ‘ਤੇ ਸਾਨੂੰ | ਮਿਲਦਾ ਹੈ :
5 x \(\frac{1}{3}\) + v = 2
ਜਾਂ v = 2 – \(\frac{5}{3}\) = \(\frac{6-5}{3}\)
ਜਾਂ v = \(\frac{1}{3}\)
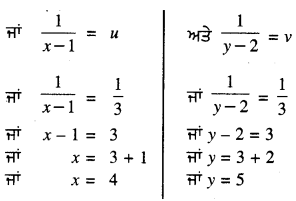
x = 4 ਅਤੇ y = 5
![]()
ਪ੍ਰਸ਼ਨ (v).
\(\frac{7x-2y}{xy}\) = 5
\(\frac{8x+7y}{xy}\) = 15
ਉੱਤਰ:
ਦਿੱਤਾ ਗਿਆ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦਾ ਜੋੜਾ ਹੈ :

\(\frac{1}{x}\) = u ਅਤੇ \(\frac{1}{y}\) = v, ਤਿਸਥਾਪਿਤ ਕਰਨ ‘ਤੇ
– 2u + 7v = 5 …..(1)
ਅਤੇ 7u + 8 = 15 …(2)
(1) ਨੂੰ 7 ਨਾਲ ਅਤੇ (2) ਨੂੰ 2 ਨਾਲ ਗੁਣਾ ਕਰਨ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
-14v + 49u = 35 ……(3)
ਅਤੇ 14v + 16u = 30 ……..(4)
ਹੁਣ (3) + (4) ਤੋਂ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
-14v + 49u = 35
14v + 16u = 30
65u = 65
u = \(\frac{65}{65}\) = 1
u ਦੇ ਮੁੱਲ ਨੂੰ (1) ਵਿੱਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
-2 (1) + 7v = 5
ਜਾਂ 7v = 5 + 2
ਜਾਂ 7v = 7
ਜਾਂ v = \(\frac{7}{7}\) = 1

x = 1 ਅਤੇ y = 1
ਪ੍ਰਸ਼ਨ (vi).
6x + 3y = 6xy
2x + 4y = 5xy
ਉੱਤਰ:
ਦਿੱਤਾ ਗਿਆ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦਾ ਜੋੜਾ ਹੈ :

\(\frac{1}{x}\) = u ਅਤੇ \(\frac{1}{y}\) = v, ਵਿੱਚ ਪ੍ਰਤਿਸਥਾਪਿਤ ਕਰਨ ‘ਤੇ
u + 2v = 2 …(1)
ਅਤੇ 4u + 2y = 5 ……(2)
ਹੁਣ (2) – (1) ਤੋਂ
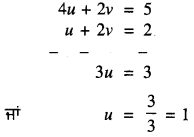
u ਜਾ ਇਹ ਮੁੱਲ (1) ਵਿੱਚ ਪ੍ਰਤਿਸਥਾਪਿਤ ਕਰਨ ‘ਤੇ
1 + 2v = 2
ਜਾਂ 2v = 2 – 1 = 1
ਜਾਂ v = \(\frac{1}{2}\)

ਹੁਣ x = 1 ਅਤੇ y = 2
![]()
ਪ੍ਰਸ਼ਨ (vii).
\(\frac{10}{x+y}\) + \(\frac{2}{x-y}\) = 4
\(\frac{15}{x+y}\) – \(\frac{5}{x-y}\) = -2
ਉੱਤਰ:
ਦਿੱਤਾ ਗਿਆ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦਾ ਜੋੜਾ ਹੈ :
\(\frac{10}{x+y}\) + \(\frac{2}{x-y}\) = 4 ਅਤੇ \(\frac{15}{x+y}\) – \(\frac{5}{x-y}\) = -2
\(\frac{1}{x+y}\) = u ਅਤੇ \(\frac{1}{x-y}\) = v ਤਿਸਥਾਪਿਤ ਕਰਨ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
10u + 2v = 4 ਜਾਂ 5u + v = 2 …(1)
15u – 5v = -2 …(2)
(1) ਨੂੰ 5 ਨਾਲ ਗੁਣਾ ਕਰਨ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
25u + 5y = 10 …(3)
(3) + (2) ਤੋਂ
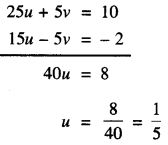
u ਨੂੰ (1) ਵਿੱਚ ਪ੍ਰਤਿਸਥਾਪਿਤ ਕਰਨ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
5\(\left(\frac{1}{5}\right)\) + v = 2
ਜਾਂ 1 + v = 2
ਜਾਂ v = 1
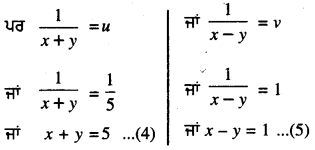
ਹੁਣ (4) + (5) ਤੋਂ ਪ੍ਰਤਿਸਥਾਪਿਤ ਕਰਨ ‘ਤੇ
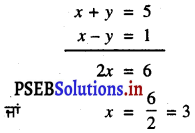
x ਦਾ ਇਹ ਮੁੱਲ (4) ਵਿੱਚ ਪ੍ਰਤਿਸਥਾਪਿਤ ਕਰਨ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
3 + y = 5
y = 5 – 3 = 2
x = 3 ਅਤੇ y = 2
ਪ੍ਰਸ਼ਨ (viii).
\(\frac{1}{3x+y}\) + \(\frac{1}{3x-y}\) = \(\frac{3}{4}\)
\(\frac{1}{2(3 x+y)}\) – \(\frac{1}{2(3 x-y)}\) = \(\frac{-1}{8}\)
ਉੱਤਰ:
ਦਿੱਤਾ ਗਿਆ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦਾ ਜੋੜਾ ਹੈ :

ਹੁਣ (1) + (2) ਤੋਂ ਪ੍ਰਤਿਸਥਾਪਿਤ ਕਰਨ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
4u + 4v = 3
4u – 4v = – 1
8u = 2
u = \(\frac{8}{2}\) = \(\frac{1}{4}\)
u ਦਾ ਮੁੱਲ (1) ਵਿੱਚ ਪ੍ਰਤਿਸਥਾਪਿਤ ਕਰਨ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
4\(\left(\frac{1}{4}\right)\) + 4v = 3
ਜਾਂ 4v = 2
ਜਾਂ v = \(\frac{2}{4}\) = \(\frac{1}{2}\)

ਹੁਣ (3) + (4) ਤੋਂ ਪ੍ਰਤਿਸਥਾਪਿਤ ਕਰਨ ’ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
3x + y = 4
3x – y = 2
6x = 6
x = 1
x ਦਾ ਮੁੱਲ (3) ਵਿਚ ਪ੍ਰਤਿਸਥਾਪਿਤ ਕਰਨ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
3 (1) + y = 4
ਜਾਂ 3 + y = 4
y = 4 – 3 = 1
x = 1 ਅਤੇ y = 1
![]()
2. ਹੇਠਾਂ ਦਿੱਤੀਆਂ ਸਮੱਸਿਆਵਾਂ ਰੇਖੀ ਸਮੀਕਰਣ ਜੋੜੇ ਦੇ ਰੂਪ ਵਿੱਚ ਦਰਸਾਓ ਅਤੇ ਉਹਨਾਂ ਦਾ ਹੱਲ ਪਤਾ ਕਰੋ :
ਪ੍ਰਸ਼ਨ (i).
ਰਿਤੂ ਧਾਰਾ ਦੀ ਦਿਸ਼ਾ ਦੇ ਅਨੁਸਾਰ 2 ਘੰਟਿਆਂ ਵਿੱਚ 20 ਕਿ.ਮੀ. ਤੈਰ ਸਕਦੀ ਹੈ ਅਤੇ ਧਾਰਾਂ ਦੀ ਦਿਸ਼ਾ ਦੇ ਉਲਟ 2 ਘੰਟਿਆਂ ਵਿੱਚ 4 ਕਿ.ਮੀ. ਤੇਰ ਸਕਦੀ ਹੈ । ਉਸਦੀ ਖੜੇ ਪਾਣੀ ਵਿੱਚ ਤੈਰਨ ਦੀ ਚਾਲ · ਗਤੀ) ਅਤੇ ਧਾਰਾਂ ਦੀ ਚਾਲ ਗਤੀ) ਪਤਾ ਕਰੋ ।
ਉੱਤਰ:
ਮੰਨ ਲਉ ਸਥਿਰ ਪਾਣੀ ਵਿਚ ਰਿਤੂ
ਦੀ ਚਾਲ = x ਕਿ.ਮੀ./ਘੰਟਾ
ਅਤੇ ਧਾਰਾ ਦੀ ਚਾਲ = y ਕਿ.ਮੀ. /ਘੰਟਾ
∴ ਧਾਰਾ ਦੀ ਦਿਸ਼ਾ ਦੇ ਉਲਟ ਚਾਲ = (x – y) ਕਿ.ਮੀ.
ਧਾਰਾ ਦੇ ਦਿਸ਼ਾ ਵਿਚ ਚਾਲ = (x + y) ਕਿ.ਮੀ.
ਰਿਤੂ ਧਾਰਾ ਦੀ ਦਿਸ਼ਾ ਵਿਚ 2 ਘੰਟੇ ਵਿੱਚ ਜਿੰਨੀ ਦੂਰੀ ਤੈਅ ਕਰਦੀ ਹੈ ।
= ਚਾਲ × ਸਮਾਂ
= (x + y) × 2 ਕਿ.ਮੀ.
ਪਹਿਲੀ ਸ਼ਰਤ ਅਨੁਸਾਰ
2 (x + y) = 20
x + y = 10 …..(1)
ਰਿਤੂ ਧਾਰਾ ਦੀ ਦਿਸ਼ਾ ਵਿਚ 2 ਘੰਟੇ ਵਿਚ ਜਿੰਨੀ ਦੂਰੀ ਤੈਅ ਕਰਦੀ ਹੈ = ਚਾਲ × ਸਮਾਂ
= 2 (x – y) ਕਿ.ਮੀ.
ਦੂਸਰੀ ਸ਼ਰਤ ਅਨੁਸਾਰ
2 (x – y) = 4
x – y = 2 …(2)
ਹੁਣ, (1) + (2) ਤੋਂ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
x + y = 10
x – y = 2
2x = 12
x = \(\frac{12}{2}\) = 6
x ਦਾ ਮੁੱਲ (1) ਵਿਚ ਪ੍ਰਤਿਸਥਾਪਿਤ ਕਰਨ ‘ਤੇ
6 + y = 10
y = 10 – 6 = 4
ਰਿਤੂ ਦੀ ਸਥਿਰ ਪਾਣੀ ਵਿਚ ਚਾਲ = 6 ਕਿ.ਮੀ. /ਘੰਟਾ
ਪਾਣੀ ਦੀ ਚਾਲ = 4 ਕਿ.ਮੀ. /ਘੰਟਾ
ਪ੍ਰਸ਼ਨ (ii).
2 ਇਸਤਰੀਆਂ ਅਤੇ 5 ਆਦਮੀ ਇਕ ਕਸੀਦੇ ਦੇ ਕੰਮ ਨੂੰ ਇਕੱਠੇ 4 ਦਿਨ ਵਿਚ ਪੂਰਾ ਕਰ ਸਕਦੇ ਹਨ, ਜਦ ਕਿ 3 ਇਸਤਰੀਆਂ ਅਤੇ 6 ਆਦਮੀ ਇਸਨੂੰ 3 ਦਿਨ ਵਿੱਚ ਪੂਰਾ ਕਰ ਸਕਦੇ ਹਨ । ਪਤਾ ਕਰੋ ਕਿ ਇਸ ਕੰਮ ਨੂੰ ਇੱਕ ਇਕੱਲੀ ਇਸਤਰੀ ਕਿੰਨੇ ਸਮੇਂ ਵਿੱਚ ਪੂਰਾ ਕਰੇਗੀ ? ਇਸ ਕੰਮ ਨੂੰ ਇਕੱਲਾ ਇੱਕ ਆਦਮੀ ਕਿੰਨੇ ਸਮੇਂ ਵਿੱਚ ਪੂਰਾ ਕਰੇਗਾ ?
ਉੱਤਰ:
ਮੰਨ ਲਉ ਇੱਕ ਇਸਤਰੀ ਕੰਮ ਕਰਦੀ ਹੈ = x ਦਿਨ
ਆਦਮੀ ਕੰਮ ਖ਼ਤਮ ਕਰਦਾ ਹੈ = y ਦਿਨ
ਇਸਤਰੀ ਦਾ ਇਕ ਦਿਨ ਦਾ ਕੰਮ = \(\frac{1}{x}\)
ਆਦਮੀ ਦਾ ਇਕ ਦਿਨ ਦਾ ਕੰਮ = \(\frac{1}{y}\)
ਪਹਿਲੀ ਸ਼ਰਤ ਅਨੁਸਾਰ
\(\frac{2}{x}\) + \(\frac{5}{y}\) = \(\frac{1}{4}\) …(1)
ਦੂਸਰੀ ਸ਼ਰਤ ਅਨੁਸਾਰ
\(\frac{3}{x}\) + \(\frac{6}{y}\) = \(\frac{1}{3}\) …..(2)
\(\frac{1}{x}\) = u ਅਤੇ \(\frac{1}{y}\) = v ਤਿਸਥਾਪਿਤ ਕਰਨ ‘ਤੇ ਸਮੀਕਰਣ (1) ਅਤੇ (2) ਤੋਂ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
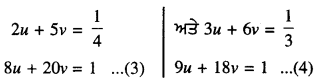
(3) ਨੂੰ 9 ਨਾਲ ਅਤੇ (4) ਨੂੰ 8 ਨਾਲ ਗੁਣਾ ਕਰਨ ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
72u + 180v = 9 …(5)
ਅਤੇ 72u + 144v = 8 …(6)
ਹੁਣ, (5) – (6) ਤੋਂ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :

v ਦੇ ਇਸ ਮੁੱਲ (4) ਵਿੱਚ ਪ੍ਰਤਿਸਥਾਪਿਤ ਕਰਨ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
9u + 18\(\left(\frac{1}{36}\right)\) = 1
ਜਾਂ 9u + \(\frac{1}{2}\) = 1
ਜਾਂ 9u = 1 – \(\frac{1}{2}\) = \(\frac{2-1}{2}\)
ਜਾਂ 9u = \(\frac{1}{2}\)
ਜਾਂ u = \(\frac{1}{2×9}\) = \(\frac{1}{18}\)

ਇੱਕ ਇਸਤਰੀ ਅਤੇ ਇੱਕ ਆਦਮੀ ਇੱਕਲੇ-ਇੱਕਲੇ ਕੰਮ ਨੂੰ ਕ੍ਰਮਵਾਰ 18 ਦਿਨ ਅਤੇ 36 ਦਿਨ ਵਿੱਚ ਪੂਰਾ ਕਰ ਸਕਦੇ ਹਨ ।
![]()
ਪ੍ਰਸ਼ਨ (iii).
ਦੀਪਿਕਾ 300 km ਦੂਰੀ ‘ਤੇ ਸਥਿਤ ਆਪਣੇ ਘਰ ਜਾਣ ਦੇ ਲਈ ਕੁੱਝ ਦੂਰੀ ਰੇਲਗੱਡੀ ਦੁਆਰਾ ਅਤੇ ਕੁੱਝ ਦੂਰੀ ਬੱਸ ਦੁਆਰਾ ਤੈਅ ਕਰਦੀ ਹੈ । ਜੇਕਰ ਉਹ 60 km ਰੇਲਗੱਡੀ ਦੁਆਰਾ ਅਤੇ ਬਾਕੀ ਬੱਸ ਦੁਆਰਾ ਤੈਅ ਕਰਦੀ ਹੈ ਤਾਂ ਉਸਨੂੰ 4 ਘੰਟੇ ਲੱਗਦੇ ਹਨ । ਜੇਕਰ ਉਹ 100 km ਦੁਬਾਰਾ ਰੇਲਗੱਡੀ ਰਾਹੀਂ ਅਤੇ ਬਾਕੀ ਯਾਤਰਾ ਬੱਸ ਦੁਆਰਾ ਕਰੇ ਤਾਂ ਉਸਨੂੰ 10 ਮਿੰਟ ਵੱਧ ਲੱਗਦੇ ਹਨ | ਰੇਲਗੱਡੀ ਅਤੇ ਬੱਸ ਦੀ ਕੁਮਵਾਰ ਚਾਲ ਪਤਾ ਕਰੋ ।
ਉੱਤਰ:
ਮੰਨ ਲਉ ਰੇਲ ਗੱਡੀ ਦੀ ਚਾਲ = x ਕਿ.ਮੀ. /ਘੰਟਾ
ਅਤੇ ਬੱਸ ਦੀ ਚਾਲ = y ਕਿ.ਮੀ. /ਘੰਟਾ
ਕੁੱਲ ਦੂਰੀ = 300 ਕਿ.ਮੀ.
ਸਥਿਤੀ I
60 ਕਿ.ਮੀ. ਦੂਰੀ ਤੈਅ ਕਰਨ ਲਈ ਲੱਗਾ ਸਮਾਂ

ਬੱਸ ਦੁਆਰਾ(= 300 – 60) 240 ਕਿ.ਮੀ. ਦੂਰੀ ਤੈਅ ਕਰਨ ਵਿਚ ਲੱਗਾ ਸਮਾਂ

ਸਥਿਤੀ II
ਰੇਲਗੱਡੀ ਦੁਆਰਾ 100 ਕਿ.ਮੀ. ਦੂਰੀ ਤੈਅ ਕਰਨ ਵਿਚ ਲੱਗਾ ਸਮਾਂ = \(\frac{100}{x}\)
ਬਸ ਦੁਆਰਾ 200 ਕਿ.ਮੀ. ਦੂਰੀ ਤੈਅ ਕਰਨ ਵਿਚ
ਲਗਾ ਸਮਾਂ = (300 – 100) = \(\frac{200}{y}\) ਘੰਟੇ
∴ ਕੁੱਲ ਸਮਾਂ = (\(\frac{100}{x}\) + \(\frac{200}{y}\))ਘੰਟੇ
ਦੂਸਰੀ ਸ਼ਰਤ ਅਨੁਸਾਰ
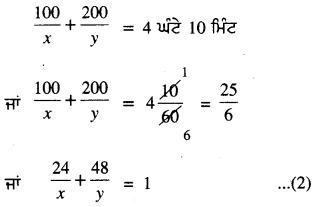
\(\frac{1}{x}\) = u ਅਤੇ \(\frac{1}{y}\) = v ਤਿਸਥਾਪਿਤ ਕਰਨ ‘ਤੇ ਅਸੀਂ ਪ੍ਰਾਪਤ ਕਰਦੇ ਹਨ :
(1) ਅਤੇ (2) ਤੋਂ
15u + 60v = 1
ਅਤੇ 24u + 48v = 1
ਜਾਂ 15u + 60v – 1 = 0
24u + 48v – 1 = 0
ਤਿਰਛੀ ਗੁਣਾ ਵਿਧੀ ਰਾਹੀਂ :
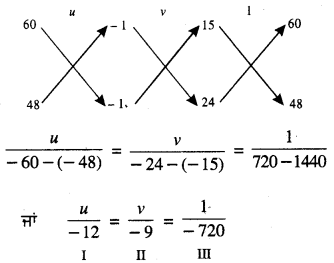
I ਅਤੇ III ਤੋਂ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :

ਰੇਲ ਗੱਡੀ ਦੀ ਚਾਲ ਅਤੇ ਬੱਸ ਦੀ ਚਾਲ ਕ੍ਰਮਵਾਰ 60 ਕਿ.ਮੀ. /ਘੰਟਾ ਅਤੇ 80 ਕਿ.ਮੀ. /ਘੰਟਾ ਹੈ ।
