Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.7 Textbook Exercise Questions and Answers.
PSEB Solutions for Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables Ex 3.7
Question 1.
The ages of two friends Ani and Biju differ by 3 years. Ani’s father Dharam is twice as old as Am and Biju Is twice as old as his sister Cathy. The ages of Cathy and Dharam differ by 30 years. Find the ages of Ani and Biju.
Solution:
Let Ani’s age = x years
and Biju’s age = y years
Dharam’s age = 2x years
Cathy’s age = years
According to 1st condition,
(Ani’s age) (Biju’s age) = 3
x – y = 3 ……………(1)
According to 2nd condition,
(Dharam’ age) – (Cathy’s age) = 30
2x – \(\frac{y}{2}\) = 30
or \(\frac{4 x-y}{2}\) = 30
or 4x – y = 60 ………….(2)
Now (2) – (1) gives,
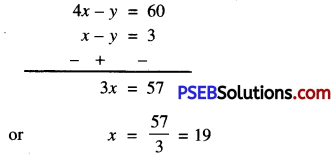
Substitute this value of x in (1), we get:
19 – y = 3
or -y = 3 – 19
or -y = -16
or y = 16
Hence, Ani’s age = 19 years
Biju’s age =16 years.
![]()
Question 2.
One says, “Give me a hundred, friend! I shall then become twice as rich as you”. The other replies, “if you give me ten, I shall be six times as rich as you.” Tell me what is the amount of their (respective) capital ? [From the Bijaganita of Bhaskara II] [Hint: x + 100 = 2(y – 100), y + 10 = 6 (x – 10)].
Solution:
Let Capital of one friend = ₹ x
and capital of 2nd friend = ₹ y
According to 1st condition
x + 100 = 2(y – 100)
or x + 100 = 2y – 200
or x – 2y = -200 – 100
or x – 2y = -300 …………..(1)
According to 2nd condition
y + 10 = 6(x – 10)
or v-f 10 = 6x – 60
or 6x – y = 10 + 60
or 6x – y = 70 ……………(2)
Multiplying (1) by 6, we get
6x – 12y = – 1800 …………….(3)
Now, (3) – (2) gives
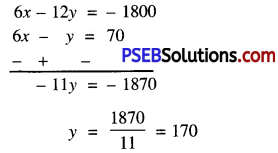
Substitute this value of y in (2), we get:
6x – 170 = 70
or 6x = 70 + 170
or 6x = 240
or x = \(\frac{240}{6}\) = 40
Hence, amount of their capital are 40 and 170 respectively.
![]()
Question 3.
A train covered a certain distance at a uniform speed. If the train would have been 10 km/b faster, It would have taken 2 hours less than the scheduled time. And, if the train were slower by 10 km/h; it would have taken 3 hours more than the scheduled time. Find the distance covered by the train.
Solution:
Let speed of train =x km/hour
and time taken by train =y hour
∴ Distance covered by train = (Speed) (Time) = (xy) km
According to 1st condition,
(x + 10)(y – 2) = xy
or xy – 2x + 10y – 20 = y
or -2x + 10y – 20 = 0
or x – 5y + 10 = 0
According to 2nd condition,
(x – 10) (y + 3) = xy
or xy + 3x – 10y – 30 = xy
or 3x – 10y – 30 = 0
Multiplying (1) by 3, we get:
3x – 15y + 30 = 0
Now, (3) – (2) gives
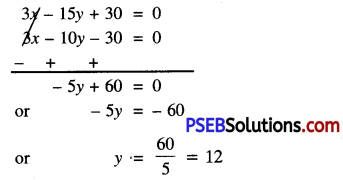
Substitute this value of y in (1), we get:
x – 5 × 12 + 10 = 0
or x – 60 + 10 = 0
or x – 50 = 0
or x = 50
Speed of train = 50 km/hour
Time taken by train = 12 hour
Hence, distance covered by train = (50 × 12) km = 600 km.
![]()
Question 4.
The students of a class are made to stand in rows. If 3 students are extra in a row, there would be 1 row less. If 3 students are less in a row, there would be 2 rows more. Find the number of students in the class.
Solution:
Let number of students in each row = x
and number of rows = y
Total number of students in the class = xy
According to 1st condition,
(x + 3) (y – 1) = xy
or xy – x + 3y – 3 = xy
or -x + 3y – 3 = 0
or x – 3y + 3 = 0
According to 2nd condition,
(x -3) (y + 2) = xy
or xy + 2x – 3y – 6= xy
or 2x – 3y – 6 = 0
Now, (2) – (1) gives

x = 9
Substitute this value of x in (1), we get:
9 – 3y + 3 = 0
or -3y + 12 = 0
or -3y = -12
or y = \(\frac{12}{3}\) = 4
∴ Number of students in each row = 9 and number of rows = 4
Hence, total number of students in the class = 9 × 4 = 36.
![]()
Question 5.
In a ∆ABC, ∠C = 3 ∠B = 2(∠A +∠B) find the three angles.
Solution:
In ∆ABC,
Given that, ∠C = 3∠B = 2(∠A + ∠B)
I II III
From II and III, we get:
3∠B =2(∠A+∠B)
or 3∠B = 2∠A + 2∠B
or 3∠B – 2∠B = 2∠A
or ∠B = 2∠A ……………..(1)
From I and II, we get:
∠C = 3∠B
or ∠C = 3(2∠A) [using (1)]
or ∠C = 6∠A …………….(2)
Sum of three angles of a triangle is 180°
∠A + ∠B + ∠C = 180°
or ∠A + 2∠A + 6∠A = 180°
or 9∠A = 180°
∠A = \(\frac{180^{\circ}}{9}\) = 20°
Hence, ∠A = 20°: ∠B =2 x 20° = 40°; ∠C = 6 x 20° = 120°.
![]()
Question 6.
Draw the graphs of the equations 5x – y = 5 and 3x – y = 3. Determine the co-ordinates of the vertices of the triangle
formed by these lines and the y axis.
Solution:
Given pair of linear equation are 5x – y = 5 and 3x – y = 3
Consider,
5x – y = 5
or 5x = 5 + y
Putting y = 0 in (1), we get:
x = \(\frac{5+0}{5}=\frac{5}{5}\)
Putting y = – 5 in (1), we get:
x = \(\frac{5-5}{5}=\frac{0}{5}\) = 0
Putting y = 5 in (1), we get:
x = \(\frac{5+5}{5}=\frac{10}{5}\) = 2

Plotting A (1, 0); B (0, — 5); C (2, 5) on the graph, we get the equation of line 5x — y = 5
and 3x – y = 3
or 3x = 3 + y
or x = \(\frac{3+y}{3}\) ……………(2)
Putting y = 0 in (2), we get:
x = \(\frac{3+0}{3}=\frac{3}{3}\) = 1
Putting y = 3 in (2), we get:
x = \(\frac{3-3}{3}=\frac{0}{3}\) = 0
Putting y = 3 in (2), we get:
x = \(\frac{3+3}{3}=\frac{6}{3}\) = 2
Table:
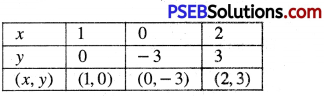
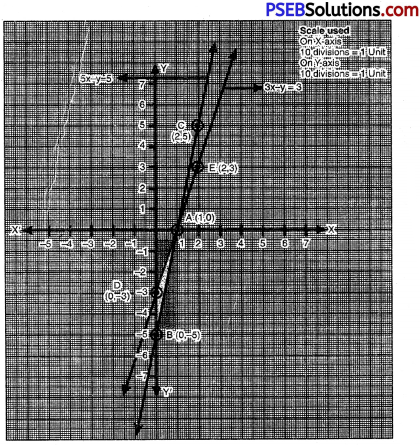
Plotting A (1, 0); D (0, -3); E (2, 3) on the graph. we get the equation of line 3x – y = 3. From the graph, it is clear that given lines intersect at A (1, 0). Triangle formed by these lines and y axis are shaded in the graph i.e. ∆ABD. Coordinates of the vertices of ∆ABD are A(1, 0); B(0, -5) and D(0, -3).
![]()
Question 7.
Solve the following pair of linear equations:
(i) px + qy = p – q
qx – py = p + q
(ii) ax + by = c
bx + ay = 1 + c
(iii) \(\frac{x}{a}-\frac{y}{b}\) = 0
ax + by = a2 + b2
(iv) (a – b)x + (a + b)y = a2 – 2ab – b2
(a + b) (x + y) = a2 + b2
(v) 152x – 378y = 74
-378x + 152y = -604
Solution:
(i) Given pair of linear equation are
px + qy = p – q …………(1)
and qx – py = p + q ………….(2)
Multiplying (1) by q and (2) by p, we get:
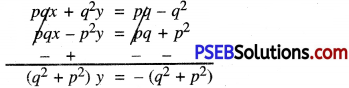
or y = -1
Substitute this value of y in (1), we get:
px + q(-1) = p – q
or px – q = p – q
or px = p – q + q
or px = p
or x = 1
Hence, x = 1 and y = -1.
![]()
(ii) Given pair of linear equation are
ax + by = c
bx + ay = 1 + c
ax + by – c = 0
bx + ay – (1 + c) = 0
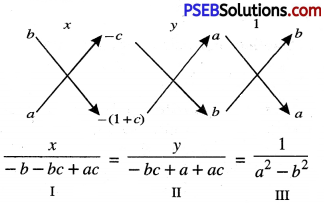
From I and III, we get:
\(\frac{x}{-b-b c+a c}=\frac{1}{a^{2}-b^{2}}\)
or x = \(\frac{a c-b c-b}{a^{2}-b^{2}}\)
From II and III, we get:
\(\frac{y}{-b c+a+a c}=\frac{1}{a^{2}-b^{2}}\)
or y = \(\frac{a+a c-b c}{a^{2}-b^{2}}\)
Hence, x = \(\frac{a c-b c-b}{a^{2}-b^{2}}\) and y = \(\frac{a+a c-b c}{a^{2}-b^{2}}\).
(iii) Given pair of linear equation are
\(\frac{x}{a}-\frac{y}{b}\) = 0
or \(\frac{b x-a y}{a b}\) = 0
or bx – ay = 0
or bx—ay = O …(1)
and ax + by = a2 + b2
or ax + by – (a2 + b2) = 0 …………..(2)
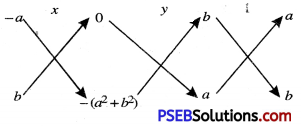
or \(\frac{x}{a\left(a^{2}+b^{2}\right)}=\frac{y}{b\left(a^{2}+b^{2}\right)}=\frac{1}{a^{2}+b^{2}}\)
or \(\frac{x}{a}=\frac{y}{b}=\frac{1}{1}\)
I II III
From I and III, we get:
\(\frac{x}{a}=\frac{1}{1}\)
⇒ x = a
From II and III, we get:
\(\frac{y}{b}=\frac{1}{1}\)
⇒ y = b
Hence, x = a, y = b.
![]()
(iv) Given pair of linear equation are
(a – b)x + (a + b)y = a2 – 2ab – b2
or ax – bx + ay + by = a2 – 2ab – b2 …………….(1)
and (a + b) (x + y) = a2 + b2
or ax + bx + ay + by = a2 + b2
Now, (1) – (2) gives

Substitute this value of x in (1), we get:
(a – b) (a + b) + (a + b) y = a2 – 2ab – b2
or a2 – b2 + (a + b) y = a2 – 2ab – b2
or (a + b) y = a2 – 2ab – b2 – a2 + b2
or (a + b)y = -2ab
or y = \(\frac{-2 a b}{a+b}\)
Hence, x = a + b and y = a + b
(v) Given pair of linear equation are
152x – 378y = – 74
and -378x + 152y = -604
or 76x – 189y + 37 = 0
and -189x + 76y + 302 = 0
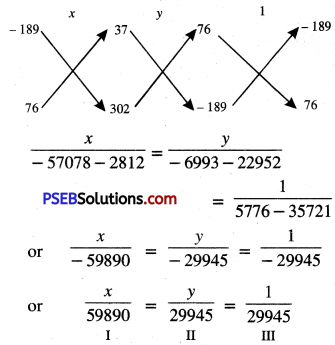
From I and III, we get:
\(\frac{x}{59890}=\frac{1}{29945}\)
⇒ x = \(\frac{59890}{29945}\)
⇒ x = 2
From II and III, we get:
\(\frac{y}{29945}=\frac{1}{29945}\)
⇒ y = \(\frac{29945}{29945}\)
⇒ y = 1
Hence x = 2 and y = 1.
![]()
Question 8.
ABCD is a cyclic quadrilateral (see Fig.). Find the angles of the cyclic quadrilateral.
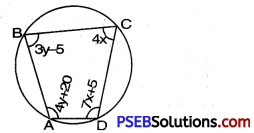
Solution:
In cyclic quadrilateral ABCD,
∠A = (4y + 20); ∠B = 3y – 5; ∠C = 4x and ∠D = 7x + 5
Sum of opposite angles of a cyclic quadrilateral are of measure 180°.
∴ ∠A + ∠C = 180°
or 4y + 20 + (4x) = 180°
or 4x + 4y = 180° – 20
or 4x + 4y = 160
or x + y = 40
or y = 40 – x ……………..(1)
and ∠B + ∠D = 180°
or 3y – 5 + (7x + 5)= 180°
or 3y – 5 + 7x + 5 = 180°
or 7x + 3y = 180° …………….(2)
Substitute the value of y from (1) in (2). we get:
7x + 3(40 – x)= 180°
or 7x + 120 – 3x = 180°
or 4x = 180 – 120
or 4x = 60
x = \(\frac{60}{4}\) = 15
Substitute this value of x in (1 ), we get:
y = 40 – 15 = 25
∴ ∠A = 4y + 20 = 4 × 25 + 20 = 120°
∠B = 3y – 5 = 3 × 25 – 5 = 70°
∠C = 4x =4 × 15 = 60°
∠D = 7x + 5 = 7 × 15 + 5 = 110°
Hence, ∠A = 120°, ∠B = 70°; ∠C = 60° and ∠D = 110°.
