PSEB 10th Class Maths Solutions Chapter 3 दो चर वाले रैखिक समीकरण युग्म Ex 3.7

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 3 दो चर वाले रैखिक समीकरण युग्म Ex 3.7 Textbook Exercise Questions and Answers

PSEB Solutions for Class 10 Maths Chapter 3 दो चर वाले रैखिक समीकरण युग्म Ex 3.7

प्रश्न 1.
दो मित्रों अनी और बीजू की आयु में 3 वर्ष का अंतर है। अनी के पिता धरम की आयु अनी की आयु की दुगुनी और बीजू की आयु अपनी बहन कैथी की आयु की दुगुनी है। कैथी और धरम की आयु का अंतर 30 वर्ष है। अनी और बीजू की आयु ज्ञात कीजिए।
हल :
मान लीजिए अनी की आयु = x वर्ष
और बीजू की आयु = y वर्ष
धर्म की आयु = 2x वर्ष
कैथी की आयु = \(\frac{1}{2}\) y वर्ष
पहली शर्त अनुसार,
(अनी की आयु) – (बीजू का आयु) = 3
x – y = 3
दूसरी शर्त अनुसार
(धर्म की आयु) – (कैथी की आयु) = 30
2x – \(\frac{y}{2}\) = 30

या \(\frac{4 x-y}{2}\) = 30
या 4x – y = 60
अब, (2) – (1) से प्राप्त होता है :

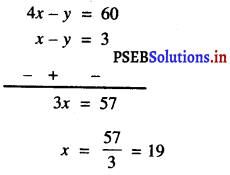
x के इस मान को (1) में प्रतिस्थापित करने पर हमें प्राप्त होता है :
19 – y = 3.
– y = 3 – 19
या – y = – 16
या y = 16
अतः, अनी की आयु = 19 वर्ष
बीजू की आयु =16 वर्ष।

प्रश्न 2.
एक मित्र दूसरे से कहता है कि, ‘यदि मुझे एक सौ दे दो, तो मैं आप से दो गुना धनी बन जाऊंगा।’ दूसरा उत्तर देता है यदि आप मुझे दस दे दें, तो मैं आप से छः गुना धनी बन जाऊँगा।’ बताइए कि उनकी क्रमशः क्या संपत्तियां हैं ? [भाष्कर I को बीज गणित से]
[संकेत 😡 + 100 = 2 (v-100),
y + 10 = 6 (x – 10)].
हल :
मान लीजिए एक मित्र की पूँजी = ₹ x
दूसरे मित्र की पूँजी = ₹ y
पहली शर्त अनुसार,
x + 100 = 2 (y – 100)
या x + 100 = 2y – 200
या x – 2y = – 200 – 100
या x – 2y = – 300 ………….(1)
दूसरी शर्त अनुसार
y + 10 = 6 (x – 10)
या y + 10 = 6x – 60
या 6x – y = 10 + 60
या 6x – y = 70 ………….(2)
(1) को 6 से गुणा करने पर हमें प्राप्त होता है:
6x – 12y = – 1800 ………….(3)
अब, (3) – (2) से प्राप्त होता है

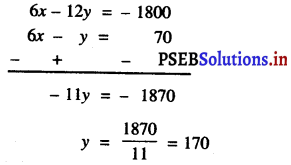
y को (2) से गुणा करने पर हमें प्राप्त होता है:
6x – 170 = 70
या 6x = 70 + 170
या 6x = 240
या x = \(\frac{240}{6}\) = 40
अतः, उनकी पूंजी क्रमश: ₹40 और ₹ 170 है।

प्रश्न 3.
एक रेलगाड़ी कुछ दूरी समान चाल से तय करती है। यदि रेलगाड़ी 10 km/h अधिक तेज चलती होती, तो उसे नियत समय से 2 घंटे कम लगते और यदि रेलगाड़ी 10 km/h धीमी चलती होती, तो उसे नियत समय से 3 घंटे अधिक लगते। रेलगाड़ी द्वारा तय की गई दूरी ज्ञात कीजिए।
हल :
मान लीजिए रेलगाड़ी की चाल = x किमी/घंटा
और रेलगाड़ी द्वारा लिया गया समय = y घंटे
∴ गाड़ी द्वारा तय की गई दूरी = (चाल) × (समय) = (xy) किमी
किमी पहली शर्त अनुसार,
(x + 10) (y – 2) = xy
या xy – 2x + 10y – 20 = xy
या – 2x + 10y – 20 = 0
या x – 5y + 10= 0
दूसरी शर्त अनुसार,
(x – 10) (y + 3) = xy
या xy + 3x – 10y – 30 = xy
या 3x – 10y – 30 = 0 ………..(2)
(1) को 3 से गुणा करने पर हमें प्राप्त होता है :
3x – 15y + 30 = 0 ………….(3)
अब, (3) – (2) से प्राप्त होता है

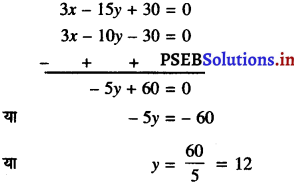
y के इस मान को (1) में प्रतिस्थापित करने पर हमें प्राप्त होता है:
x – 5 × 12 + 10 = 0
x – 60 + 10 = 0
x – 50 = 0
x = 50
∴ रेलगाड़ी की चाल = 50 किमी/घंटा
रेलगाड़ी द्वारा लिया गया समय = 12 घंटे
अतः, रेलगाड़ी द्वारा तय की गई दूरी = (50 × 12) किमी = 600 किमी.

प्रश्न 4.
एक कक्षा के विद्यार्थियों को पंक्तियों में खड़ा होना है। यदि पंक्ति में 3 विद्यार्थी अधिक होते, तो 1 पंक्ति कम होती। यदि पंक्ति में 3 विद्यार्थी कम होते, तो 2 पैंक्तियाँ अधिक बनतीं। कक्षा में विद्यार्थियों की संख्या ज्ञात कीजिए।
हल :
मान लीजिए प्रत्येक पक्ति में विद्यार्थियों की संख्या = x
और पंक्तियों की संख्या = y
कक्षा में विद्यार्थियों की संख्या = xy
पहली शर्त अनुसार
(x + 3) (y – 1) = xy
या xy – x + 3y – 3 = xy
या – x + 3y – 3 = 0
या x – 3y + 3 = 0 …………(1)
दूसरी शर्त अनुसार
(x – 3) (y + 2) = xy
या xy + 2x – 3y – 6 = xy
या 2x – 3y – 6 = 0 ……………(2)
अब, (2) – (1) से प्राप्त होता है :

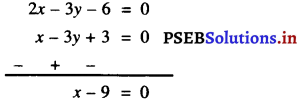
x = 9
x को (1) में प्रतिस्थापित करने पर हमें प्राप्त होता है।
9 – 3y + 3 = 0
या – 3y + 12 = 0
या – 3y = – 12
या y = \(\frac{12}{3}\) = 4
∴ प्रत्येक पंक्ति में विद्यार्थियों की संख्या = 9 और
पंक्तियों की संख्या = 4
अतः, कक्षा में विद्यार्थियों की संख्या = 9 × 4 = 36.

प्रश्न 5.
एक ∆ABC में, ∠C = 3 ∠B = 2 (∠A + ∠B) है। त्रिभुज के तीनों कोण ज्ञात कीजिए।
हल :
एक ∠ABC में,
∠C = 3∠B = 2 (∠A + ∠B)
I II III
II और III, से हमें प्राप्त होता है
3∠B = 2 (∠A + ∠B)
या 3∠B = 2∠A + 2∠B
या 3∠B – 2∠B = 2∠A
या ∠B = 2∠A ……………(1)
I और II, से हमें प्राप्त होता है
∠C = 3∠B
या ∠C = 3(2∠A)
[(1) का प्रयोग करने पर ]
या ∠C = 6∠A …………..(2)
त्रिभुज के तीनों कोणों का योगफल 180° होता है
∠A + ∠B + ∠C = 180°
या ∠A + 2∠A + 6∠A = 180°
9∠A = 180°
या ∠A = 180 = 20°
∠A = 20°; ∠B = 2 × 20° = 40°
∠C = 6 × 20° = 120°.

प्रश्न 6.
समीकरणों 5x – y = 5 और 3x – y = 3 के ग्राफ खींचिए। इन रेखाओं और y-अक्ष से बने त्रिभुज के शीर्षों के निर्देशांक ज्ञात कीजिए। इस प्रकार बने त्रिभुज के क्षेत्रफल का परिकलन कीजिए।
हल :
दिया गया रैखिक समीकरण युग्म है : 5x – y = 5 और 3x – y = 3
5x – y = 5
5x = 5 + y
x = \(\frac{5+y}{5}\) ……………(1)
y = 0 को (1), रखने पर, हमें प्राप्त होता है :

x = \(\frac{5+0}{5}=\frac{5}{5}\) = 1

y = – 5 को (1) में रखने पर, हमें प्राप्त होता है :

x = \(\frac{5-5}{5}=\frac{0}{5}\) = 0

y = 5 को (1) में रखने पर, हमें प्राप्त होता है :

x = \(\frac{5+5}{5}=\frac{10}{5}\) = 2

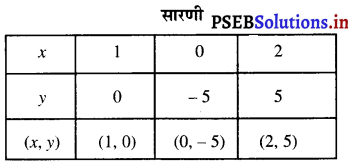
बिंदुओं A (1, 0); B (0, – 5); C (2, 5) को ग्राफ पर आलेखित करने पर हमें समीकरण 5x – y = 5 की रेखा प्राप्त होती है।
और 3x – y = 3
या 3x = 3 +y
या x = \(\frac{3+y}{3}\) ………….(2)
y = 0 को (2) में रखने पर, हमें प्राप्त होता है :

x = \(\frac{3+0}{3}=\frac{3}{3}\) = 1

y = – 3 को (2) में रखने पर, हमें प्राप्त होता है :

x = \(\frac{3-3}{3}=\frac{0}{3}\) = 0

y = 3 को (2) में रखने पर, हमें प्राप्त होता है :

x = \(\frac{3+3}{3}=\frac{6}{3}\) = 2

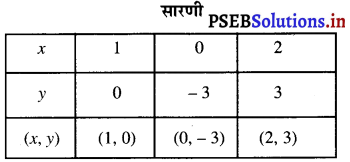
बिंदुओं A (1, 0); D (0, – 3); E (2, 3) को ग्राफ पेपर आलेखित करने पर हमें समीकरण 3x – y = 3 की रेखा प्राप्त होती है :

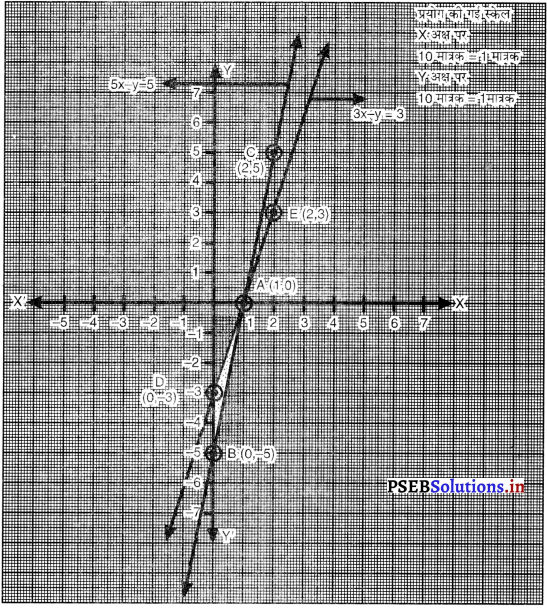
ग्राफ से यह स्पष्ट है कि दी गई रेखाएँ A (1, 0) पर प्रतिच्छेद करती हैं। इन रेखाओं और ‘-अक्ष से बनी ∆ABD को छायांकित किया गया है। ∆ABD के शीर्षों के निर्देशांक हैं : A (1, (0); B (0, – 5) और D (0, – 3)

प्रश्न 7.
निम्न रैखिक समीकरणों के युग्मों को हल कीजिए :
(i) px + qy = p – q
qx – py = p + q

(ii) ax + by = c
bx + ay = 1 + c

(iii) \(\frac{x}{a}-\frac{y}{b}\) = 0
ax + by = a² + b²

(iv) (a – b)x + (a + b) y = a² – 2ab – b²
(a + b) (x + y) = a² + b²

(v) 152x – 378y = – 74
– 378x + 152 y = – 604
हल :
(i) दिया गया रैखिक समीकरण युग्म है :
px + qy = p – q ………….(1)
और qx – py = p + q ………..(2)

(1) को q से और (2) को p से गुणा करने पर हमें प्राप्त होता है।

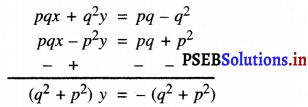
या y = – 1

y के इस मान को (1) में प्रतिस्थापित करने पर हमें प्राप्त होता है :
px + q (- 1) = p – q
या px – q = p – q
या px = p – q + q
या px = p
या x = 1
अतः, x = 1 और y = – 1

(ii) दिया गया रैखिक समीकरण युग्म है :
ax + by = c
और bx + ay = 1 + c
या ax + by – c = 0

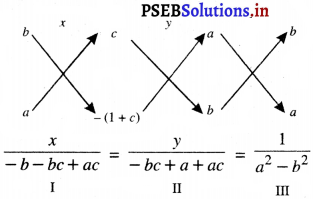
I और III से हमें प्राप्त होता है :

\(\frac{x}{-b-b c+a c}=\frac{1}{a^{2}-b^{2}}\)

या x = \(\frac{a c-b c-b}{a^{2}-b^{2}}\)

II और III से हमें प्राप्त होता है :

\(\frac{y}{-b c+a+a c}=\frac{1}{a^{2}-b^{2}}\)

या y = \(\frac{a+a c-b c}{a^{2}-b^{2}}\)

अत: x = \(\frac{a c-b c-b}{a^{2}-b^{2}}\) और y = \(\frac{a+a c-b c}{a^{2}-b^{2}}\)

(iii) दिया गया रैखिक समीकरण युग्म है :
\(\frac{x}{a}-\frac{y}{b}\) = 0

या \(\frac{b x-a y}{a b}\) = 0
या bx – ay = 0 …………..(1)
या ax + by = a² + b²
या ax + by – (a² + b²) = 0 …………(2)

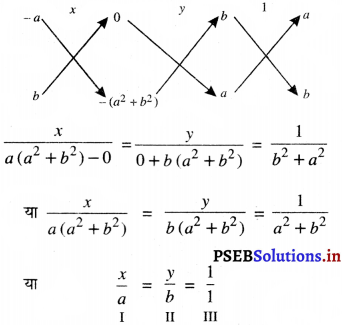
I और III से हमें प्राप्त होता है :

\(\frac{x}{a}=\frac{1}{1}\)

⇒ x = a

II और III से हमें प्राप्त होता है :

\(\frac{y}{b}=\frac{1}{1}\)

⇒ y = b

अतः, x = a और y = b.

(iv) दिया गया रैखिक समीकरण युग्म है :
(a – b)x + (a + b) y = a² – 2ab – b²
या ax – bx + ay + by = a² – 2ab – b² ………….(1)
और (a + b) (x + y) = a² + b²
या ax + bx + ay + by = a² + b² ………….(2)
अब, (1) – (2) से प्राप्त होता है:

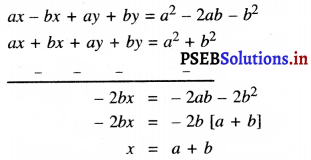
x के इस मान को (1) में प्रतिस्थापित करने पर हमें प्राप्त होता है :
(a – b) (a + b) + (a + b) y = a² – 2ab – b²
या a² – b² + (a + b) y = a² – 2ab – b²
या (a + b) y = a² – 2ab – b² – a² + b²
या (a + b) y = – 2ab
या y = \(\frac{-2 a b}{a+b}\)
अतः, x = a + b और y = 4.

(v) दिया गया रैखिक समीकरण युग्म है :
152x – 378y = – 74 और – 378x + 152y = – 604
या 76x – 189y + 37 = 0 और – 189x + 76y + 302 = 0

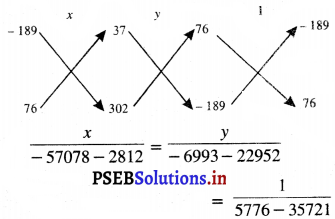
या \(\frac{x}{-59890}=\frac{y}{-29945}=\frac{1}{-29945}\)

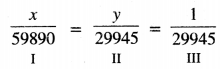
I और III से हमें प्राप्त होता है
\(\frac{x}{59890}=\frac{1}{29945}\)

⇒ x = \(\frac{59890}{29945}\)

⇒ x = 2

II और III से हमें प्राप्त होता है
\(\frac{y}{29945}=\frac{1}{29945}\)

⇒ y = \(\frac{29945}{29945}\)

⇒ y = 1
अतः, x = 2 और y = 1

प्रश्न 8.
ABCD एक चक्रीय चतुर्भुज है। (देखिए आकृति)। इस चक्रीय चतुर्भुज के कोण ज्ञात कीजिए।

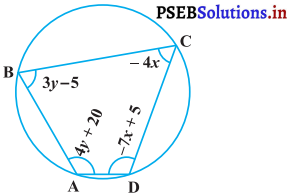
हल :
चक्रीय चतुर्भुज ABCD में,
∠A = (4y + 20);
∠B = 3y – 5;
∠C = 4x और
∠D = 7x + 5
∠C = 4x = 4 × 15 = 60°
∠D = 7x + 5 = 7 × 15 + 5 = 110°
अतः, ∠A = 120°, ∠B = 70°; ∠C = 60° और ∠D = 110°.
∠A + ∠C = 180°
या 4y + 20 + (4x) = 180°
या 4x + 4y = 180° – 20
या 4x + 4y = 160
या x + y = 40
या y = 40 – x …………………(1)
और ∠B + ∠D = 180°
या 3y – 5 + (7x + 5) = 180°
या 3y – 5 + 7x + 5 = 180°
या 7x + 3y = 180° …………..(2)
(1) से , के इस मान को (2) में प्रतिस्थापित करने पर हमें प्राप्त होता है :
7x + 3 (40 – x) = 180°
7x + 120 – 3x = 180
या 4x = 180 – 120
या 4x = 60
या x = \(\frac{60}{4}\) = 15
x के इस मान को (1) में प्रतिस्थापित करने पर हमें प्राप्त होता है:
y = 40 – 15 = 25 .
∴ ∠A = 4y + 20
= 4 × 25 + 20 = 120°
∠B = 3y – 5 = 3 × 25 – 5 = 70°
∠C = 4x = 4 × 15 = 60°
∠D = 7x + 5 = 7 × 15 + 5 = 110°
अंत:- ∠A = 120°, ∠B = 70°; ∠C = 60° और ∠D = 110°.