PSEB 10th Class Maths Solutions Chapter 3 ਦੋ ਚਲਾਂ ਵਿੱਚ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦੇ ਜੋੜੇ Ex 3.7

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 3 ਦੋ ਚਲਾਂ ਵਿੱਚ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦੇ ਜੋੜੇ Ex 3.7 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 10 Maths Chapter 3 ਦੋ ਚਲਾਂ ਵਿੱਚ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦੇ ਜੋੜੇ Exercise 3.7

ਪ੍ਰਸ਼ਨ 1.
ਦੋ ਦੋਸਤਾਂ ਹਨੀ ਅਤੇ ਸੰਨੀ ਦੀ ਉਮਰ ਵਿਚ 3 ਸਾਲ ਦਾ ਅੰਤਰ ਹੈ । ਹਨੀ ਦੇ ਪਿਤਾ ਹਰਮਿੰਦਰ ਦੀ ਉਮਰ ਹਨੀ ਦੀ ਉਮਰ ਤੋਂ ਦੁੱਗਣੀ ਹੈ ਅਤੇ ਸੰਨੀ ਦੀ ਉਮਰ ਆਪਣੀ ਭੈਣ ਨੂੰ ਤੋਂ ਦੁੱਗਣੀ ਹੈ । ਗੁਨੂੰ ਅਤੇ ਹਰਮਿੰਦਰ ਦੀ ਉਮਰ ਵਿੱਚ 30 ਸਾਲ ਦਾ ਅੰਤਰ ਹੈ । ਹਨੀ ਅਤੇ ਸੰਨੀ ਦੀ ਉਮਰ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਮੰਨ ਲਉ ਹਨੀ ਦੀ ਉਮਰ = x ਸਾਲ
ਅਤੇ ਸੰਨੀ ਦੀ ਉਮਰ = y ਸਾਲ
ਹਰਮਿੰਦਰ ਦੀ ਉਮਰ = 2x ਸਾਲ
ਗੁਨੂੰ ਦੀ ਉਮਰ = \(\frac{1}{2}\)y ਸਾਲ
ਪਹਿਲੀ ਸ਼ਰਤ ਅਨੁਸਾਰ
ਹਨੀ ਦੀ ਉਮਰ – ਸੰਨੀ ਦੀ ਉਮਰ = 3 ਸਾਲ
x – y = 3 …(1)
ਦੂਸਰੀ ਸ਼ਰਤ ਅਨੁਸਾਰ
ਹਰਮਿੰਦਰ ਦੀ ਉਮਰ – ਗਨੂੰ ਦੀ ਉਮਰ = 30 ਸਾਲ
2x – \(\frac{y}{2}\) = 30
ਜਾਂ \(\frac{4x-y}{2}\) = 30
ਜਾਂ 4x – y = 60 ….(2)
ਹੁਣ, (2) – (1) ਤੋਂ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।

x ਦਾ ਮੁੱਲ (1) ਵਿੱਚ ਤਿਸਥਾਪਿਤ ਕਰਨ ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
19 – y = 3
ਜਾਂ -y = 3 – 19
ਜਾਂ -y = – 16
ਜਾਂ y = 16
ਹਨੀ ਦੀ ਉਮਰ = 19 ਸਾਲ
ਸੰਨੀ ਦੀ ਉਮਰ =16 ਸਾਲ

ਪ੍ਰਸ਼ਨ 2.
ਇਕ ਮਿੱਤਰ ਦੂਸਰੇ ਨੂੰ ਕਹਿੰਦਾ ਹੈ ਕਿ, “ਜੇਕਰ | ਤੁਸੀਂ ਮੈਨੂੰ ਇੱਕ ਸੌ ਰੁਪਏ ਦੇ ਦਿਉ ਤਾਂ ਮੇਰੇ ਕੋਲ ਤੁਹਾਡੇ ਨਾਲੋਂ ਦੋ ਗੁਣਾ ਪੈਸੇ ਹੋ ਜਾਣਗੇ | ਦੂਸਰਾ ਕਹਿੰਦਾ ਹੈ ਕਿ | ‘‘ਜੇਕਰ ਤੁਸੀਂ ਮੈਨੂੰ ₹ 10 ਦੇ ਦਿਉ ਤਾਂ ਮੈਂ ਤੁਹਾਡੇ ਤੋਂ ਛੇ ਗੁਣਾ ਅਮੀਰ ਹੋ ਜਾਵਾਂਗਾ ” ਪਤਾ ਕਰੋ ਉਹਨਾਂ ਕੋਲ ਕੁਮਵਾਰ ਕਿੰਨੇ ਪੈਸੇ ਹਨ ? (ਭਾਸ਼ਕਰ II ਦੇ ਬੀਜ ਗਣਿਤ ਤੋਂ)
[ਸੰਕੇਤ : x + 100 = 2(y – 100),
y + 10 = 6 (x – 10)].
ਹੱਲ:
ਮੰਨ ਲਉ ਇਕ ਮਿੱਤਰ ਕੋਲ ਪੈਸੇ = ₹ x
ਦੂਸਰੇ ਮਿੱਤਰ ਕੋਲ ਪੈਸੇ = ₹ y
ਪਹਿਲੀ ਸ਼ਰਤ ਅਨੁਸਾਰ
x + 100 = 2 (y – 100)
ਜਾਂ x + 100 = 2y – 200
ਜਾਂ x – 2y = – 200 – 100
ਜਾਂ x – 2y = – 300 ….(1)
ਦੂਸਰੀ ਸ਼ਰਤ ਅਨੁਸਾਰ
y + 10 = 6 (x – 10)
ਜਾਂ y + 10 = 6x – 60
ਜਾਂ 6x – y = 10 + 60
ਜਾਂ 6x – y = 70 ….(2)
(1) ਨੂੰ 6 ਨਾਲ ਗੁਣਾ ਕਰਨ ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
6x – 12y = – 1800 …(3)
ਹੁਣ (3) – (2) ਤੋਂ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :

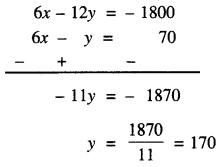
y ਨੂੰ (2) ਨਾਲ ਗੁਣਾ ਕਰਨ ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
6x – 170 = 70
ਜਾਂ 6x = 70 + 170
ਜਾਂ 6x = 240
ਜਾਂ x = \(\frac{240}{6}\) = 40
ਪਹਿਲੇ ਮਿੱਤਰ ਕੋਲ ਪੈਸੇ : ₹ 40
ਦੁਸਰੇ ਮਿੱਤਰ ਕੋਲ ਪੈਸੇ : ₹ 170 ਹੈ ।

ਪ੍ਰਸ਼ਨ 3.
ਇੱਕ ਰੇਲਗੱਡੀ ਕੁੱਝ ਦੂਰੀ ਇਕ ਸਮਾਨ ਚਾਲ ਨਾਲ ਤੈਅ ਕਰਦੀ ਹੈ । ਜੇਕਰ ਗੱਡੀ ਦੀ ਗਤੀ 10 km/h ਵਧਾ ਦਿੱਤੀ ਜਾਵੇ ਤਾਂ ਉਹ ਉੱਨੀ ਦੂਰੀ ਲਈ 2 ਘੰਟੇ ਘੱਟ ਸਮਾਂ ਲਵੇਗੀ ਅਤੇ ਜੇਕਰ ਰੇਲਗੱਡੀ ਦੀ ਗਤੀ 10 km/h ਘਟਾ ਦਿੱਤੀ ਜਾਵੇ ਤਾਂ ਉਹ ਉੱਨੀ ਦੂਰੀ ਲਈ 3 ਘੰਟੇ ਵੱਧ ਸਮਾਂ ਲਵੇਗੀ 1 ਰੇਲਗੱਡੀ ਦੁਆਰਾ ਤੈਅ ਕੀਤੀ ਦੂਰੀ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਮੰਨ ਲਉ ਰੇਲਗੱਡੀ ਦੀ ਚਾਲ = x ਕਿ.ਮੀ. /ਘੰਟਾ
ਰੇਲਗੱਡੀ ਦੁਆਰਾ ਲਿਆ ਗਿਆ ਸਮਾਂ = y ਘੰਟਾ
∴ ਰੇਲਗੱਡੀ ਦੁਆਰਾ ਤੈਅ ਕੀਤੀ ਦੂਰੀ
= ਚਾਲ × ਸਮਾਂ
= (xy) ਕਿਮੀ
ਪਹਿਲੀ ਸ਼ਰਤ ਅਨੁਸਾਰ
(x + 10) (y – 2) = xy
ਜਾਂ y – 2x + 10y – 20 = xy
ਜਾਂ – 2x + 10y – 20 = 0
ਜਾਂ x – 5y + 10 = 0 ……(1)
ਦੂਸਰੀ ਸ਼ਰਤ ਅਨੁਸਾਰ
(x – 10) (y + 3) = xy
ਧੀ xy + 3x – 10y – 30 = xy
ਜਾਂ 3x – 10y – 30 = 0 …(2)
(1) ਨੂੰ 3 ਨਾਲ ਗੁਣਾ ਕਰਨ ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
3x – 15y + 30 = 0 ….(3)
ਹੁਣ, (3) – (2) ਤੋਂ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :

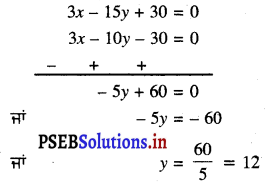
y ਦਾ ਇਹ ਮੁੱਲ (1) ਵਿੱਚ ਰੱਖਣ ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
x – 5 × 12 + 10 = 0
ਜਾਂ x – 60 + 10 = 0
ਜਾਂ x – 50 = 0
ਜਾਂ x = 50
∴ ਰੇਲਗੱਡੀ ਦੀ ਚਾਲ = 50 ਕਿ.ਮੀ. /ਘੰਟਾ
ਰੇਲਗੱਡੀ ਦੁਆਰਾ ਲਿਆ ਗਿਆ ਸਮਾਂ = 12 ਬੰਟੇ
ਰੇਲਗੱਡੀ ਦੁਆਰਾ ਤੈਅ ਕੀਤੀ ਦੂਰੀ
= (50 × 12) ਕਿ.ਮੀ.
= 600 ਕਿ.ਮੀ.

ਪ੍ਰਸ਼ਨ 4.
ਇਕ ਜਮਾਤ ਵਿੱਚ ਵਿਦਿਆਰਥੀਆਂ ਨੂੰ ਪੰਗਤੀਆਂ ਵਿਚ ਖੜਾ ਕਰਨਾ ਹੈ । ਜੇਕਰ ਪੰਗਤੀਆਂ ਵਿਚ 3 ਵਿਦਿਆਰਥੀ ਵੱਧ ਹੁੰਦੇ ਤਾਂ ਇੱਕ ਪੰਗਤੀ ਘੱਟ ਹੁੰਦੀ । ਜੇਕਰ ਪੰਗਤੀ ਵਿਚ 3 ਵਿਦਿਆਰਥੀ ਘੱਟ ਹੁੰਦੇ, ਤਾਂ 2 ਪੰਗਤੀਆਂ ਵੱਧ ਬਣਦੀਆਂ ਜਮਾਤ ਵਿੱਚ ਵਿਦਿਆਰਥੀਆਂ ਦੀ ਗਿਣਤੀ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਮੰਨ ਲਉ ਹਰ ਇੱਕ ਪੰਗਤੀ ਵਿਚ ਵਿਦਿਆਰਥੀਆਂ ਦੀ ਗਿਣਤੀ = x
ਅਤੇ ਪੰਗਤੀਆਂ ਦੀ ਗਿਣਤੀ = y
ਜਮਾਤ ਵਿਚ ਵਿਦਿਆਰਥੀਆਂ ਦੀ ਗਿਣਤੀ = xy
ਪਹਿਲੀ ਸ਼ਰਤ ਅਨੁਸਾਰ
(x + 3) (y – 1) = xy
ਜਾਂ xy – x + 3y – 3 = xy
ਜਾਂ -x + 3y – 3 = 0
ਜਾਂ x – 3y + 3 = 0 …(1)
ਦੂਸਰੀ ਸ਼ਰਤ ਅਨੁਸਾਰ
(x – 3) (y + 2) = xy
ਜਾਂ xy + 2x – 3y – 6 = xy
ਜਾਂ 2x + 3y – 6 = 0 …(2)
ਹੁਣ, (2) – (1) ਤੋਂ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :

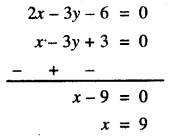
x ਦਾ ਮੁੱਲ (1) ਵਿੱਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
9 – 3y + 3 = 0
ਜਾਂ -3y + 12 = 0
ਜਾਂ -3y = – 12
ਜਾਂ y = \(\frac{12}{3}\) = 4
∴ ਹਰ ਇੱਕ ਪੰਗਤੀ ਵਿਚ ਵਿਦਿਆਰਥੀਆਂ ਦੀ ਗਿਣਤੀ = 9
ਪੰਗਤੀਆਂ ਦੀ ਗਿਣਤੀ = 4
ਜਮਾਤ ਵਿਚ ਵਿਦਿਆਰਥੀਆਂ ਦੀ ਗਿਣਤੀ
= 9 × 4 = 36

ਪ੍ਰਸ਼ਨ 5.
ਇੱਕ △ABC ਵਿੱਚ ∠C = 3 ∠B = 2 (∠A + ∠B) ਹੈ ।ਤ੍ਰਿਭੁਜ ਦੇ ਤਿੰਨੋਂ ਕੋਣ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਇਕ △ABC ਵਿੱਚ
∠C = 3∠B = 2 (∠A + ∠B)
I II III
II ਅਤੇ III, ਤੋਂ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
3∠B = 2 (∠A + ∠B)
ਜਾਂ 3∠B = 2∠A + 2∠B
ਜਾਂ 3∠B – 2∠B = 2∠A
ਜਾਂ ∠B = 2∠A
I ਅਤੇ II, ਤੋਂ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
∠C = 3∠B
ਜਾਂ ∠C = 3(2∠A)
[(1) ਦਾ ਪ੍ਰਯੋਗ ਕਰਨ ਤੇ ]
ਜਾਂ ∠C = 6∠A …..(2)
ਤਿਭੁਜ ਦੇ ਤਿੰਨਾਂ ਕੋਣਾਂ ਦਾ ਜੋੜ 180° ਹੁੰਦਾ ਹੈ ।.
∠A + ∠B + ∠C = 180°
ਜਾਂ ∠A + 2∠A + 6∠A = 180°
ਜਾਂ 9∠A = 180°
ਜਾਂ ∠A = \(\frac{180^{\circ}}{9}\) = 20°
∠A = 20°; ∠B = 2 × 20° = 40°
∠C = 6 × 20° = 120°.

ਪ੍ਰਸ਼ਨ 6.
ਸਮੀਕਰਣਾਂ 5r – y = 5 ਅਤੇ 3x – y = 3 ਦੇ ਗ੍ਰਾਫ ਖਿੱਚੋ । ਇਹਨਾਂ ਰੇਖਾਵਾਂ ਅਤੇ y-ਧੁਰੇ ਨਾਲ ਬਣੇ ਤਿਭਜ ਦੇ ਸਿਖਰਾਂ ਦੇ ਨਿਰਦੇਸ਼ ਅੰਕ ਅਤੇ ਤਿਭੁਜ ਦ ਖੇਤਰਫਲ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਦਿੱਤਾ ਹੋਇਆ ਰੇਖੀ ਸਮੀਕਰਣ ਜੋੜਾ ਹੈ :
5x – y = 5 ਅਤੇ 3x – y = 3
5x – y = 5
ਜਾਂ 5x = 5 + y
ਜਾਂ x = \(\frac{5+y}{5}\) …(1)
y = 0 ਨੂੰ (1), ਵਿੱਚ ਰੱਖਣ ’ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
x = \(\frac{5+0}{5}\) = \(\frac{5}{5}\) = 1
y = -5 ਨੂੰ (1) ਵਿੱਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
x = \(\frac{5-5}{5}\) = \(\frac{0}{5}\) = 0
y = 5 ਨੂੰ (1) ਵਿੱਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
x = \(\frac{5+5}{5}\) = \(\frac{10}{5}\) = 2
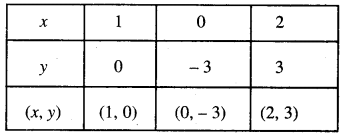
ਸਾਰਣੀ

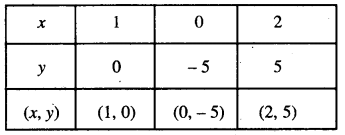
ਬਿੰਦੁਆਂ A (1, 0); B (0, – 5); C (2, 5) ਦੇ ਗਾਫ਼ ਨੂੰ ਆਲੇਖਿਤ ਕਰਨ ਤੇ ਸਾਨੂੰ ਸਮੀਕਰਣ 5x – y = 5 ਦੀ ਰੇਖਾ ਪ੍ਰਾਪਤ ਹੁੰਦੀ ਹੈ ।
ਅਤੇ 3x – y = 3
ਜਾਂ 3x = 3 + y
ਜਾਂ x = \(\frac{3+y}{3}\) ….(2)
y = 0 ਨੂੰ (2) ਵਿੱਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
x = \(\frac{3+0}{3}\) = \(\frac{3}{3}\) = 1
y = -3 ਨੂੰ (2) ਵਿੱਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
x = \(\frac{3-3}{3}\) = \(\frac{0}{3}\) = 0
y = 3 ਨੂੰ (2) ਵਿੱਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
x = \(\frac{3+3}{3}\) = \(\frac{6}{3}\) = 2

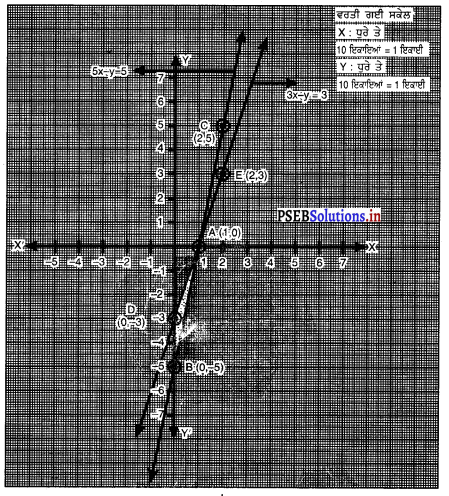
ਬਿੰਦੁਆਂ A (1, 0); D (0, – 3); E (2, 3) ਨੂੰ ਗ੍ਰਾਫ਼ ਪੇਪਰ ਤੇ ਆਲੇਖਿਤ ਕਰਨ ਤੇ ਸਾਨੂੰ ਸਮੀਕਰਣ 3x – y = 3 ਦੀ ਰੇਖਾ ਪ੍ਰਾਪਤ ਹੁੰਦੀ ਹੈ ।
ਗ੍ਰਾਫ਼ ਤੋਂ ਇਹ ਸਪੱਸ਼ਟ ਹੈ ਕਿ ਦਿੱਤੀਅ ਹੋਈ ਹਥਾਵਾਂ -A (1, 0) ਉੱਤੇ ਕੱਟਦੀਆਂ ਹਨ ।y- ਧੂਰੇ ਤੇ ਬਣੀ △ABD ਨੂੰ ਛਾਇਆ ਅੰਕਿਤ ਕੀਤਾ ਗਿਆ ਹੈ । △ABD ਦੇ ਸਿਖ਼ਰਾਂ ਦੇ ਨਿਰਦੇਸ਼ ਅੰਕ ਹਨ : A (1, 0); B (0, – 5) ਅਤੇ D (0, – 3)
ਸਾਰਣੀ

7. ਹੇਠਾਂ ਦਿੱਤੇ ਰੇਖੀ ਸਮੀਕਰਣ ਜੋੜਿਆਂ ਨੂੰ ਹੱਲ ਕਰੋ :

ਪ੍ਰਸ਼ਨ (i).
px + qy = p – q
qx – py = p + q
ਉੱਤਰ:
ਦਿੱਤਾ ਗਿਆ ਰੇਖੀ ਸਮੀਕਰਣ ਜੋੜਾ ਹੈ :
px + qy = p – q ..(1)
ਅਤੇ qx – py = p + q …(2)
(1) ਨੂੰ q ਨਾਲ ਅਤੇ (2) ਨੂੰ p ਨਾਲ ਗੁਣਾ ਕਰਨ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :

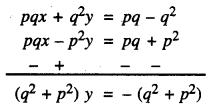
ਜਾਂ y = -1
y ਦਾ ਇਹ ਮੁੱਲ (1) ਵਿਚ ਸਥਾਪਿਤ ਕਰਨ ‘ਤੇ | ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
px + q(-1) = p – qx
ਜਾਂ px – q = p – q
ਜਾਂ px = p – q + q
ਜਾਂ px = p
ਜਾਂ x = 1
∴ x = 1 ਅਤੇ y = – 1

ਪ੍ਰਸ਼ਨ (ii).
ax + by = c
bx + ay = 1 + c
ਉੱਤਰ:
ਦਿੱਤਾ ਗਿਆ ਰੇਖੀ ਸਮੀਕਰਣ ਜੋੜਾ ਹੈ :
ax + by = c
ਅਤੇ bx + ay = 1 + c
ਜਾਂ ax + by – c = 0
ਅਤੇ bx + ay – (1 + c) = 0

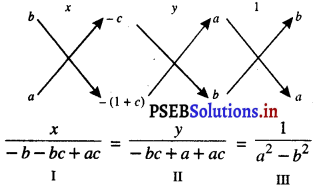
I ਅਤੇ III ਤੋਂ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :

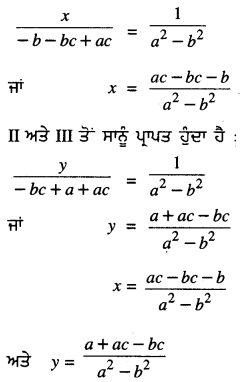
ਪ੍ਰਸ਼ਨ (iii).
\(\frac{x}{a}\) – \(\frac{y}{b}\) =0
ax + by = a² + b²
ਉੱਤਰ:
ਦਿੱਤਾ ਗਿਆ ਰੇਖੀ ਸਮੀਕਰਣ ਜੋੜਾ ਹੈ :
\(\frac{x}{a}\) – \(\frac{y}{b}\) = 0
ਜਾਂ \(\frac{bx-ay}{ab}\) = 0
ਜਾਂ bx – ay = 0 ….(1)
ਅਤੇ ax + by = a² + b²
ਜਾਂ ax + by = (a² + b²) = 0 …..(2)
ਤਿਰਛੀ ਗੁਣਾ ਵਿਧੀ ਦੁਆਰਾ

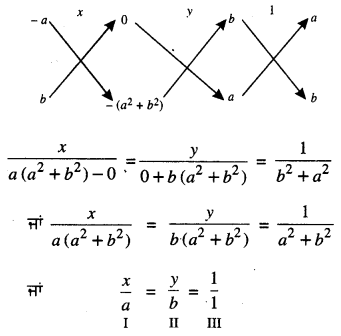
I ਅਤੇ III ਤੋਂ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
\(\frac{x}{a}\) = \(\frac{1}{1}\) ⇒ x = a
II ਅਤੇ III ਤੋਂ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
\(\frac{y}{b}\) = \(\frac{1}{1}\) ⇒ y = b
x = a ਅਤੇ y = b

ਪ੍ਰਸ਼ਨ (iv).
(a – b)x + (a + b) y = a² – 2ab – b²
(a + b) (x + y) = a² + b²
ਉੱਤਰ:
ਦਿੱਤਾ ਗਿਆ ਰੇਖੀ ਸਮੀਕਰਣ ਜੋੜਾ ਹੈ :
(a – b)x + (a + b) y = a² – 2ab – b²
ਜਾਂ ax – bx + ay + by = a² – 2ab – b² …(1)
ਅਤੇ (a + b) (x + y) = a² + b²
ਜਾਂ ax + bx + ay + by = a² + b² …(2)
ਹੁਣ (1) – (2) ਤੋਂ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :

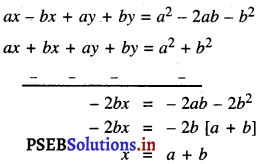
x ਦਾ ਮੁੱਲ (1) ਵਿੱਚ ਰੱਖਣ ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
(a – b) (a + b) + (a + b) y = a² – 2ab – b²
ਜਾਂ a² – b² + (a + b) y = a² – 2ab – b²
ਜਾਂ (a + b) y = a² – 2ab – b² – a² + b²
ਜਾਂ (a + b) y = – 2ab
ਜਾਂ y = \(\frac{-2ab}{a+b}\)
x = a + b ਅਤੇ y = \(\frac{-2ab}{a+b}\)

ਪ੍ਰਸ਼ਨ (v).
152x – 378y = -74
– 378x + 152y =- 604
ਉੱਤਰ:
ਦਿੱਤਾ ਗਿਆ ਰੇਖੀ ਸਮੀਕਰਣ ਜੋੜਾ ਹੈ :
152x – 378y = – 74
ਅਤੇ – 378x + 152y = – 604
ਜਾਂ 76x – 189y + 37 = 0
ਅਤੇ – 189x + 76y + 302 = 0
ਤਿਰਛੀ ਗੁਣਾ ਵਿਧੀ ਦੁਆਰਾ

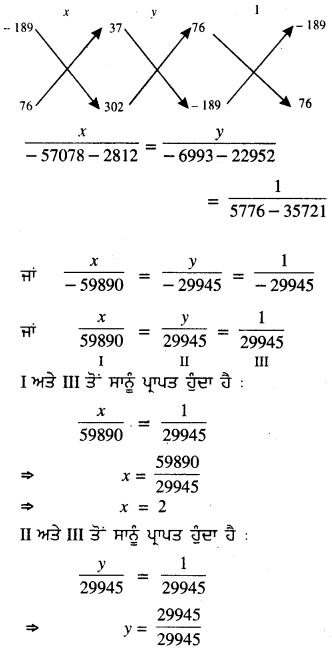
⇒ y = 1
x = 2 ਅਤੇ y = 1

ਪ੍ਰਸ਼ਨ 8.
ABCD ਇੱਕ ਚੱਕਰੀ ਚਤੁਰਭੁਜ ਹੈ । ਇਸ ਚੱਕਰੀ ਚਤੁਰਭੁਜ ਦੇ ਕੋਣ ਪਤਾ ਕਰੋ । (ਦੇਖੋ ਚਿੱਤਰ)

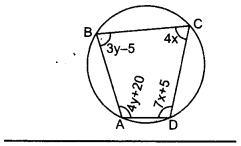
ਹੱਲ:
ਚੱਕਰੀ ਚਤੁਰਭੁਜ ABCD ਵਿੱਚ
∠A = (4y + 20); ∠B = 3y – 5;
∠C = 4x ਅਤੇ ∠D = 7x + 5
∠C = 4x = 4 x 15 = 60°
∠D = 7x + 5 = 7 x 15 + 5 = 110°
∠A = 120°, ∠B = 70°; ∠C = 60°
ਅਤੇ ∠D = 110°
∴ ∠A + ∠C = 180°,
ਜਾਂ 4y + 20 + (4x) = 180°
ਜਾਂ 4x + 4y = 180° – 20°
ਜਾਂ 4x + 4y = 160
ਜਾਂ x + y = 40
ਜਾਂ y = 40 – x ….(1)
ਅਤੇ ∠B + ∠D = 180°
ਜਾਂ 3y – 5 + (7x + 5) = 180°
ਜਾਂ 3y – 5 + 7x + 5 = 180°
ਜਾਂ 7x + 3y = 180° …(2)
(1) ਤੋਂy ਦਾ ਮੁੱਲ (2) ਵਿਚ ਰੱਖਣ ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
7x + 3 (40 – x) = 180°
ਜਾਂ 7x + 120 – 3x = 180
ਜਾਂ 4x = 180 – 120
ਜਾਂ 4x = 60
ਜਾਂ x = \(\frac{60}{4}\) = 15
x ਦਾ ਇਹ ਮੁੱਲ (1) ਵਿੱਚ ਪ੍ਰਤਿਸਥਾਪਿਤ ਕਰਨ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ !
y = 40 – 15 = 25
∴ ∠A = 4y + 20 = 4 × 25 + 20
= 120°
∠B = 3y – 5 = 3 × 25 – 5 = 70°
∠C = 4x = 4 × 15 = 60°
∠D = 7x + 5 = 7 × 15 + 5 = 110°
∴ ∠A = 120°, ∠B = 70°; ∠C = 60°
ਅਤੇ ∠D = 110°