PSEB 10th Class Maths Solutions Chapter 4 ਦੋ ਘਾਤੀ ਸਮੀਕਰਣ Ex 4.3

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 4 ਦੋ ਘਾਤੀ ਸਮੀਕਰਣ Ex 4.3 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 10 Maths Chapter 4 ਦੋ ਘਾਤੀ ਸਮੀਕਰਣ Exercise 4.3

1. ਜੇਕਰ ਹੇਠ ਲਿਖਿਆਂ ਸਮੀਕਰਣਾਂ ਦੇ ਮੂਲ ਸੰਭਵ ਹੋਣ ਤਾਂ ਪੂਰਨ ਵਰਗ ਬਣਾਉਣ ਦੀ ਵਿਧੀ ਰਾਹੀਂ ਪਤਾ ਕਰੋ ।

ਪ੍ਰਸ਼ਨ (i).
2x² – 7x + 3 = 0
ਉੱਤਰ:
ਦਿੱਤੀ ਗਈ ਸਮੀਕਰਣ ਹੈ
2x² – 7x + 3 = 0
ਜਾਂ 2x² – 7x = – 3


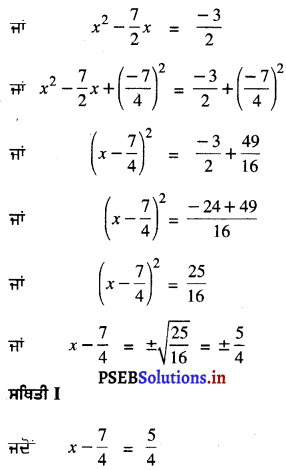
ਇਸ ਲਈ, ਦਿੱਤੀ ਗਈ ਦੋ ਘਾਤੀ ਸਮੀਕਰਣ ਦੇ ਮੂਲ 3, \(\frac{1}{2}\) ਹਨ

ਪ੍ਰਸ਼ਨ (ii).
2x² + x – 4 = 0
ਉੱਤਰ:
ਦਿੱਤੀ ਗਈ ਸਮੀਕਰਣ ਹੈ
2x² + x – 4 = 0
ਜਾਂ 2x² + x = 4


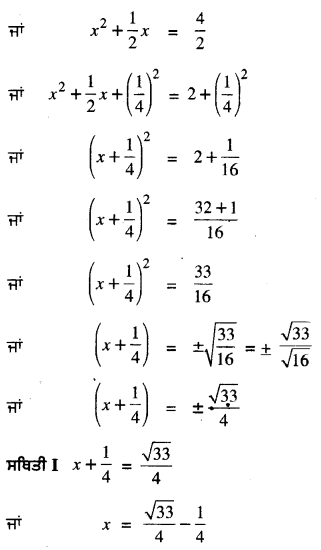
ਇਸ ਲਈ, ਦਿੱਤੀ ਗਈ ਦੋ ਘਾਤੀ ਸਮੀਕਰਣ ਦੇ ਮੂਲ ਹਨ: \(\frac{-1+\sqrt{33}}{4}\) ਅਤੇ \(\frac{-1-\sqrt{33}}{4}\)

ਪ੍ਰਸ਼ਨ (iii).
4x² + 4\(\sqrt {3}\) x + 3 = 0
ਉੱਤਰ:
ਦਿੱਤੀ ਗਈ ਦੋ ਘਾਤੀ ਸਮੀਕਰਣ ਹੈ
4x² + 4\(\sqrt {3}\)x + 3 = 0
ਜਾਂ 4x² + 4\(\sqrt {3}\)x = – 3

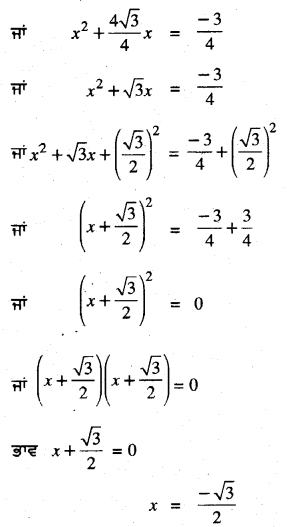
ਜਾਂ x + \(\frac{\sqrt{3}}{2}\) = 0
ਜਾਂ x = \(\frac{-\sqrt{3}}{2}\)
ਇਸ ਲਈ, ਦਿੱਤੀ ਗਈ ਸਮੀਕਰਣ ਦੇ ਮੂਲ ਹਨ :
\(\frac{-\sqrt{3}}{2}\) ਅਤੇ \(\frac{-\sqrt{3}}{2}\)

ਪ੍ਰਸ਼ਨ (iv).
2x² + x + 4 = 0
ਉੱਤਰ:
ਦਿੱਤੀ ਹੋਈ ਦੋ ਘਾਤੀ ਸਮੀਕਰਣ ਹੈ
2x² + x + 4 = 0
ਜਾਂ 2x² + x = -4

∵ ਕਿਸੇ ਸੰਖਿਆਂ ਦਾ ਵਰਗ ਰਿਣਾਤਮਕ ਨਹੀਂ ਹੋ ਸਕਦਾ ।
∴ (x + \(\frac{1}{4}\))², x ਦੇ ਕਿਸੇ ਵੀ ਮੁੱਲ ਲਈ ਰਿਣਾਤਮਕ ਨਹੀਂ ਹੋ ਸਕਦਾ ।
∴ ਇੱਥੇ x ਦਾ ਕੋਈ ਵਾਸਤਵਿਕ ਮੁਲ ਨਹੀਂ ਹੈ ਜੋ ਦੋ ਘਾਤੀ ਸਮੀਕਰਣ ਨੂੰ ਸੰਤੁਸ਼ਟ ਕਰਦਾ ਹੈ ।
∴ ਇਸਦੇ ਮੂਲ ਵਾਸਤਵਿਕ ਨਹੀਂ ਹਨ ।

ਪ੍ਰਸ਼ਨ 2.
ਉਪਰੋਕਤ ਪ੍ਰਸ਼ਨ (1) ਵਿੱਚ ਦਿੱਤੇ ਗਏ ਦੋ ਘਾਤੀ | ਸਮੀਕਰਣਾਂ ਦੇ ਮੂਲ ਦੋ ਘਾਤੀ ਸੂਤਰ ਦਾ ਪ੍ਰਯੋਗ ਕਰਕੇ ਪਤਾ ਲਗਾਉ ॥
ਹੱਲ:
(i) ਦਿੱਤੀ ਗਈ ਦੋ ਘਾਤੀ ਸਮੀਕਰਣ ਹੈ
2x² – 7x + 3 = 0
ਇਸਦੀ ax² + bx + c = 0 ਨਾਲ ਤੁਲਨਾ ਕਰਨ ਤੇ ।
a = 2, b = – 7, c = 3
ਹੁਣ b² – 4ac = (-7) – 4 × 2 × 3
= 49 – 24
= 25 > 0

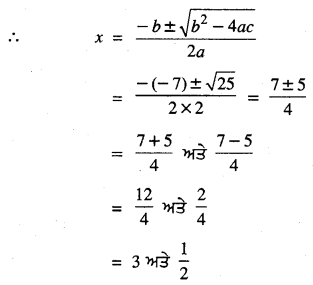
∴ 3 ਅਤੇ \(\frac{1}{2}\)ਦਿੱਤੀ ਗਈ ਸਮੀਕਰਣ ਦੇ ਮੂਲ ਹਨ ।

(ii) ਦਿੱਤੀ ਗਈ ਦੋ ਘਾਤੀ ਸਮੀਕਰਣ ਹੈ
2x² + x – 4 = 0
ਇਸ ਦੀ ਤੁਲਨਾ ax² + bx + c = 0 ਨਾਲ ਕਰਨ ਤੇ
∴ a = 1, b = 1, c = – 4
ਹੁਣ b² – 4ac = (1)² – 4 × 2 × (-4)
= 1 + 32
= 33 > 0

ਇਸ ਲਈ \(\frac{-1+\sqrt{33}}{4}\) ਅਤੇ \(\frac{-1-\sqrt{33}}{4}\) ਦਿੱਤੀ ਹੋਈ ਸਮੀਕਰਣ ਦੇ ਮੂਲ ਹਨ ।

(iii) ਦਿੱਤੀ ਗਈ ਦੋ ਘਾਤੀ ਸਮੀਕਰਣ ਹੈ
4x² + 4\(\sqrt {3}\) + 3 = 0
ਇਸ ਦੀ ਤੁਲਨਾ ax² + bx + = 0 ਨਾਲ ਕਰਨ ਤੇ :
∴ a = 4, b = 4\(\sqrt {3}\) , c = 3
ਹੁਣ b² – 4ac = (4\(\sqrt {3}\))² – 4 × 4 × 3
= 48 – 48 = 0

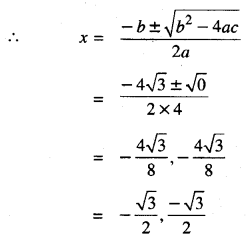
\(\frac{-\sqrt{3}}{2}\) ਅਤੇ \(\frac{-\sqrt{3}}{2}\) ਦਿੱਤੀ ਗਈ ਸਮੀਕਰਣ ਦੇ ਮੂਲ ਹਨ ।

(iv) ਦਿੱਤੀ ਗਈ ਦੋ ਘਾਤੀ ਸਮੀਕਰਣ ਹੈ
2x² + x + 4 = 0
ਇਸ ਦੀ ਤੁਲਨਾ ax² + bx + 0 = 0 ਨਾਲ ਕਰਨ ਤੇ
∴ a = 2, b = 1, c = 4
ਹੁਣ b² – 4ac = (1)² – 4 × 2 × 4
= 1 – 32 = – 31 < 0
∴ x = \(\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}\)
ਕਿਉਂਕਿ ਇਕ ਵਾਸਤਵਿਕ ਸੰਖਿਆ ਦਾ ਵਰਗ ਰਿਣਾਤਮਕ ਨਹੀਂ ਹੋ ਸਕਦਾ ਹੈ । ਇਸ ਲਈ x ਦਾ ਕੋਈ ਵਾਸਤਵਿਕ ਮੂਲ ਹੀਂ ਹੈ !
∴ ਦਿੱਤੀ ਹੋਈ ਸਮੀਕਰਣ ਦੇ ਮੂਲ ਵਾਸਤਵਿਕ ਨਹੀਂ ਹਨ ।
ਉਪਰ ਦਿੱਤੇ ਦੋ ਪ੍ਰਸ਼ਨਾਂ ਵਿਚ ਅਸੀਂ ਦੋ ਘਾਤੀ ਸਮੀਕਰਣ ਦੇ ਮੁਲ ਪਤਾ ਕਰਨ ਲਈ ਦੋਵਾਂ ਵਿਧੀਆਂ ਦਾ ਪ੍ਰਯੋਗ ਕੀਤਾ ਹੈ । ਅਸੀਂ ਦੇਖਦੇ ਹਾਂ ਕਿ ਦੋ ਘਾਤੀ ਸੂਤਰ ਦਾ ਪ੍ਰਯੋਗ, ਪੂਰਨ ਵਰਗ ਬਣਾਉਣ ਨਾਲੋਂ ਜ਼ਿਆਦਾ ਅਸਾਨ ਹੈ ।

3. ਹੇਠਾਂ ਲਿਖੀਆਂ ਸਮੀਕਰਣਾਂ ਦੇ ਮੂਲ ਪਤਾ ਕਰੋ :

ਪ੍ਰਸ਼ਨ (i).
x – \(\frac{1}{x}\) = 3, x ≠ 0
ਉੱਤਰ:
ਦਿੱਤੀ ਗਈ ਸਮੀਕਰਣ ਹੈ
x – \(\frac{1}{x}\) = 3
ਜਾਂ \(\frac{x^{2}-1}{x}\) = 3
ਜਾਂ x² – 1 = 3x
ਜਾਂ x² – 3x – 1 = 0
ਇਸ ਦੀ ਤੁਲਨਾ ax² + bx + c = 0 ਨਾਲ ਕਰਨ ਤੇ
∴ a = 1, b = – 3, c = – 1
ਹੁਣ b² – 4ac = (-3)² – 4. 1 (-1)
= 9 + 4 = 13 > 0

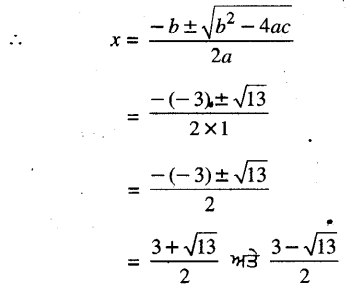
ਇਸ ਲਈ \(\frac{3+\sqrt{13}}{2}\) ਅਤੇ \(\frac{3-\sqrt{13}}{2}\) ਦਿੱਤੀ ਗਈ ਦੋ ਘਾਤੀ ਸਮੀਕਰਣ ਦੇ ਮੂਲ ਹਨ ।

ਪ੍ਰਸ਼ਨ (ii).
\(\frac{1}{x+4}\) – \(\frac{1}{x-7}\) = \(\frac{11}{30}\), x ≠ -4, 7
ਉੱਤਰ:
ਦਿੱਤੀ ਹੋਈ ਸਮੀਕਰਣ ਹੈ
\(\frac{1}{x+4}\) – \(\frac{1}{x-7}\) = \(\frac{11}{30}\)
ਜਾਂ \(\frac{(x-7)-(x+4)}{(x+4)(x-7)}\) = \(\frac{11}{30}\)

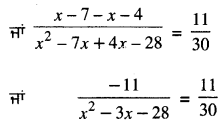
ਜਾਂ -11 × 30 = 11 (x² – 3x – 28)
ਜਾਂ x² – 3x – 28 + 30 = 0
ਜਾਂ x² – 3x + 2 = 0
ਇਸ ਦੀ ਤੁਲਨਾ ax² + bx + c = 0 ਨਾਲ ਕਰਨ ਤੇ
∴ a = 1, b = – 3, c = 2
ਹੁਣ, b² – 4ac = (-3)² – 4 × 1 × 2
= 9 – 8
= 1 > 0

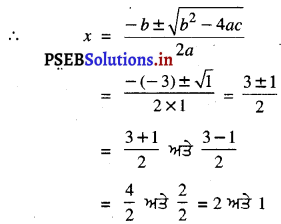
∴ 2 ਅਤੇ 1 ਦਿੱਤੀ ਹੋਈ ਸਮੀਕਰਣ ਦੇ ਮੂਲ ਹਨ ।

ਪ੍ਰਸ਼ਨ 4.
3 ਸਾਲ ਪਹਿਲਾਂ ਰਹਿਮਾਨ ਦੀ ਉਮਰ (ਸਾਲਾਂ ਵਿੱਚ) ਅਤੇ ਹੁਣ ਤੋਂ ਪੰਜ ਸਾਲ ਬਾਅਦ ਦੀ ਉਮਰ ਦੇ ਉਲਟਮਾਂ ਦਾ ਜੋੜ \(\frac{1}{3}\) ਹੈ । ਉਸ ਦੀ ਵਰਤਮਾਨ ਉਮਰ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਮੰਨ ਲਓ ਰਹਿਮਾਨ ਦੀ ਵਰਤਮਾਨ ਉਮਰ = x ਸਾਲ
3 ਸਾਲ ਪਹਿਲਾਂ ਰਹਿਮਾਨ ਦੀ ਉਮਰ = (x – 3) ਸਾਲ
ਹੁਣ ਤੋਂ 5 ਸਾਲ ਬਾਅਦ ਰਹਿਮਾਨ ਦੀ ਉਮਰ = (x + 5) ਸਾਲ
ਪ੍ਰਸ਼ਨ ਅਨੁਸਾਰ
\(\frac{1}{x-3}\) + \(\frac{1}{x+5}\) = \(\frac{1}{3}\)

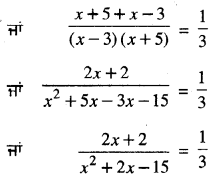
ਜਾਂ 6x + 6 = x² + 2x – 15
ਜਾਂ x² + 2x – 15 – 6x – 6 = 0
ਜਾਂ x² – 4x – 21 = 0, ਜੋ ਕਿ 1 ਵਿਚ ਦੋ ਘਾਤ ਹੈ ਇਸ ਲਈ ਇਸ ਦੀ ਤੁਲਨਾ ax² + bx + c = 0 ਨਾਲ ਕਰਨ ਤੇ
∴ a = 1, b = – 4, c = – 21
ਹੁਣ b² – 4ac = (-4)² – 4 × 1 × (21)
= 16 + 84
= 100 > 0

= 7 ਅਤੇ – 2
∵ ਉਮਰ ਰਿਣਾਤਮਕ ਨਹੀਂ ਹੋ ਸਕਦੀ ਹੈ
∴ x = – 3 ਨੂੰ ਛੱਡ ਦਿੰਦੇ ਹਾਂ
∴ x = 7
∴ ਰਹਿਮਾਨ ਦੀ ਵਰਤਮਾਨ ਉਮਰ x = 7 ਸਾਲ ।

ਪ੍ਰਸ਼ਨ 5.
ਇਕ ਸ਼੍ਰੇਣੀ ਟੈਸਟ ਵਿਚ ਸ਼ੈਫਾਲੀ ਦੇ ਗਣਿਤ ਅਤੇ ਅੰਗ੍ਰੇਜ਼ੀ ਵਿਚ ਪ੍ਰਾਪਤ ਕੀਤੇ ਅੰਕਾਂ ਦਾ ਜੋੜ 30 ਹੈ । ਜੇਕਰ ਉਸ ਨੂੰ ਗਣਿਤ ਵਿਚ 2 ਅੰਕ ਵੱਧ ਅਤੇ ਅੰਗ੍ਰੇਜ਼ੀ ਵਿਚ 3 ਅੰਕ ਘੱਟ ਮਿਲੇ ਹੁੰਦੇ ਤਾਂ ਉਸਦੇ ਅੰਕਾਂ ਦਾ ਗੁਣਨਫਲ 20 ਹੁੰਦਾ । ਉਸ ਦੁਆਰਾ ਦੋਵੇਂ ਵਿਸ਼ਿਆਂ ਵਿਚ ਪ੍ਰਾਪਤ ਅੰਕ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਮੰਨ ਲਓ ਸ਼ੈਫਾਲੀ ਨੇ ਗਣਿਤ ਵਿਚ ਪ੍ਰਾਪਤ ਕੀਤੇ ਅੰਕ = x
∴ ਸ਼ੈਫਾਲੀ ਦੇ ਅੰਗ੍ਰੇਜ਼ੀ ਵਿਚ ਪ੍ਰਾਪਤ ਅੰਕ = 30 – x
ਪ੍ਰਸ਼ਨ ਦੀ ਸ਼ਰਤ ਅਨੁਸਾਰ
ਸ਼ੈਫਾਲੀ ਦੇ ਗਣਿਤ ਵਿਚ ਅੰਕ = x + 2
ਸ਼ੈਫਾਲੀ ਦੇ ਅੰਗੇਜ਼ੀ ਵਿੱਚ ਅੰਕ
= 30 – x – 3
= 27 – 1
∴ ਉਸਦੇ ਅੰਕਾਂ ਦਾ ਗੁਣਨਫਲ = (x + 27) (27 – x)
= 27x – x² + 54 – 2x
= -x² + 25x + 54
ਪ੍ਰਸ਼ਨ ਦੀ ਦੂਸਰੀ ਸ਼ਰਤ ਅਨੁਸਾਰ
-x² + 25x + 54 = 210
ਜਾਂ -x² + 25x + 54 – 210 = 0
ਜਾਂ -x² + 25x – 156 = 0
ਜਾਂ x² – 25x + 156 = 0
ਇਸ ਦੀ ਤੁਲਨਾ ax² + bx + c = 0 ਨਾਲ ਕਰਨ ਤੇ
a = 1, b = – 25, c = 156
ਹੁਣ b² – 4ac = (-25)² – 4 × 1 × 156
= 625 – 624
= 1 > 0

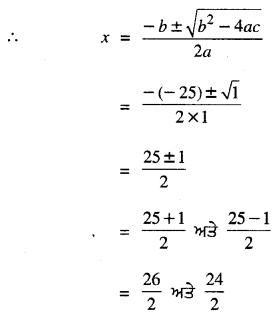
= 13 ਅਤੇ 12
ਸਥਿਤੀ I.
ਜਦੋਂ x = 13
∴ ਸ਼ੈਫਾਲੀ ਦੇ ਗਣਿਤ ਦੇ ਅੰਕ = 13
ਸ਼ੈਫਾਲੀ ਦੇ ਅੰਗ੍ਰੇਜ਼ੀ ਦੇ ਅੰਕ = 30 – 13 = 17
ਸਥਿਤੀ II.
ਜਦੋਂ = 12
ਸ਼ੈਫਾਲੀ ਦੇ ਗਣਿਤ ਦੇ ਅੰਕ = 12
ਅੰਗ੍ਰੇਜ਼ੀ ਦੇ ਅੰਕ = 30 – 12 = 18
∴ ਸ਼ੈਫਾਲੀ ਦੇ ਦੋ ਵਿਸ਼ਿਆਂ ਦੇ ਅੰਕ ਹਨ : 13 ਅਤੇ 17 ਜਾਂ 12 ਅਤੇ 18

ਪ੍ਰਸ਼ਨ 6.
ਇਕ ਆਇਤਾਕਾਰ ਖੇਤ ਦਾ ਵਿਕਰਣ ਉਸਦੀ ਛੋਟੀ ਭੁਜਾ ਤੋਂ 60 m ਲੰਬਾ ਹੈ । ਜੇਕਰ ਵੱਡੀ ਭੁਜਾ ਛੋਟੀ ਭੁਜਾ ਤੋਂ 30 m ਵੱਧ ਹੋਵੇ ਤਾਂ ਖੇਤ ਦੀਆਂ ਭੁਜਾਵਾਂ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਮੰਨ ਲਓ ਆਇਤਾਕਾਰ ਖੇਤ ਦੀ ਛੋਟੀ ਭੁਜਾ
= AD = x m

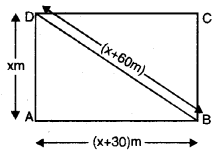
ਆਇਤਾਕਾਰ ਖੇਤ ਦੀ ਵੱਡੀ ਭੁ
= AB = (x + 30) m
ਆਇਤਾਕਾਰ ਖੇਤ ਦਾ ਵਿਕਰਣ
= DB = (x+ 60) m
ਇਕ ਆਇਤ ਵਿਚ ਲੰਬਾਈ ਅਤੇ ਚੌੜਾਈ ਦੇ ਵਿਚ ਦਾ } ਕੋਣ ਸਮਕੋਣ ਹੁੰਦਾ ਹੈ
∴ ∠AB = 90°
ਹੁਣ ਸਮਕੋਣ ਤ੍ਰਿਭੁਜ DAB ਵਿਚ
ਪਾਇਥਾਗੋਰਸ ਦੇ ਸਿਧਾਂਤ ਅਨੁਸਾਰ
(DB)² = (AD)² + (AB)²
(x + 60)² = (x)² + (x + 30)²
ਜਾਂ x² + 3600 + 120x
= x² + x² + 900 + 60x
ਜਾਂ x² + 3600 + 120x – 2x² – 900 – 60x = 0
ਜਾਂ -x² + 6x + 2700 = 0
ਜਾਂ x² – 60x – 2700 = 0
ਇਸ ਦੀ ਤੁਲਣਾ ax² + bx + c = 0 ਨਾਲ ਕਰਨ ਤੇ
∴ a = 1, b = – 60, c = – 2700
ਅਤੇ b² – 4ac = (-60)² – 4 . 1. (-2700)
= 3600 + 10800
= 14400 > 0

= 90 ਅਤੇ -30
∵ ਕਿਸੇ ਖੇਤ ਦੀ ਭੁਜਾ ਰਿਣਾਤਮਕ ਨਹੀਂ ਹੋ ਸਕਦੀ
∴ ਅਸੀਂ x = -30 ਨੂੰ ਛੱਡ ਦਿੰਦੇ ਹਾਂ
∴ x = 90
∴ ਆਇਤਾਕਾਰ ਖੇਤ ਦੀ ਸਭ ਤੋਂ ਛੋਟੀ ਭੁਜਾ
= 90 m
ਆਇਤਾਕਾਰ ਖੇਤ ਦੀ ਸਭ ਤੋਂ ਵੱਡੀ ਭੁਜਾ
= (9) + 30)
= 120 m

ਪ੍ਰਸ਼ਨ 7.
ਦੋ ਸੰਖਿਆਵਾਂ ਦੇ ਵਰਗਾਂ ਦਾ ਅੰਤਰ 180 ਹੈ । ਛੋਟੀ ਸੰਖਿਆ ਦਾ ਵਰਗ, ਵੱਡੀ ਸੰਖਿਆ ਦਾ ਅੱਠ ਗੁਣਾ ਹੈ । ਦੋਵੇਂ ਸੰਖਿਆਵਾਂ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਮੰਨ ਲਓ ਵੱਡੀ ਸੰਖਿਆ = 1
ਛੋਟੀ ਸੰਖਿਆ =y ਪ੍ਰਸ਼ਨ ਦੀ ਸ਼ਰਤ ਅਨੁਸਾਰ
x² – y² = 180 ….(i)
ਪ੍ਰਸ਼ਨ ਦੀ ਦੂਸਰੀ ਸ਼ਰਤ ਅਨੁਸਾਰ
² = 8z …(ii)
(i) ਅਤੇ (ii) ਤੋਂ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
x² – 8x = 180
ਜਾਂ x² – 8x – 180 = 0
ਇਸਦੀ ਤੁਲਨਾ ax² + bx + c = 0 ਨਾਲ ਕਰਨ ਤੇ
a = 1, b = – 8, c = – 180
ਅਤੇ b² – 4ac = (-8)² – 4 × 1 × (-180)
= 64 + 720
= 784 > 0

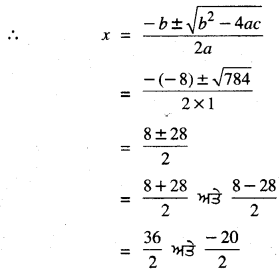
= 18 ਅਤੇ – 10
ਜਦੋਂ x = – 10 ਤਾਂ, (ii) ਤੋਂ
y² = 8 (-10) = – 80, ਜੋ ਸੰਭਵ ਨਹੀਂ ਹੈ
∴ ਅਸੀਂ x = – 10 ਨੂੰ ਛੱਡ ਦਿੰਦੇ ਹਾਂ
ਜਦੋਂ x = 18, ਤਾਂ (2) ਤੋਂ,
y² = (18) 8 = 144
ਜਾਂ y = ±\(\sqrt {144}\)
ਜਾਂ y = ±12
∴ ਲੋੜੀਂਦੀਆਂ ਸੰਖਿਆਵਾਂ ਹਨ 18 ਅਤੇ 12 ਜਾਂ 18 ਅਤੇ – 12

ਪ੍ਰਸ਼ਨ 8.
ਇੱਕ ਰੇਲਗੱਡੀ ਇੱਕ ਸਮਾਨ ਚਾਲ ਨਾਲ 360 km ਦਾ ਸਫ਼ਰ ਤੈਅ ਕਰਦੀ ਹੈ । ਜੇਕਰ ਇਹ ਚਾਲ 5 km/h ਵੱਧ ਹੁੰਦੀ ਤਾਂ ਉਹ ਉਸੇ ਸਫ਼ਰ ਲਈ 1 ਘੰਟਾ ਘੱਟ ਸਮਾਂ ਲੈਂਦੀ । ਰੇਲਗੱਡੀ ਦੀ ਚਾਲ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਮੰਨ ਲਓ ਰੇਲਗੱਡੀ ਦੀ ਇਕ ਸਮਾਨ ਚਾਲ = x km/h
ਰੇਲਗੱਡੀ ਦੁਆਰਾ ਤੈਅ ਕੀਤੀ ਦੂਰੀ = 360 km

ਰੇਲਗੱਡੀ ਦੀ ਵੱਧੀ ਹੋਈ ਚਾਲ = (x + 5) km/h
∴ ਵੱਧੀ ਹੋਈ ਚਾਲ ਨਾਲ ਰੇਲਗੱਡੀ ਦੁਆਰਾ ਲੱਗਿਆ ਸਮਾਂ
= \(\frac{360}{x+5}\)
ਪ੍ਰਸ਼ਨ ਅਨੁਸਾਰ
\(\frac{360}{x}\) – \(\frac{360}{x+5}\) = 1
\(\frac{360(x+5)-360 x}{x(x+5)}\) = 1
\(\frac{360 x+1800-360 x}{x^{2}+5 x}\) = 1
1800 = x² + 5x
x² + 5x – 1800 = 0
ਇਸ ਦੀ ਤੁਲਨਾ ax² + bx + c = 0 ਨਾਲ ਕਰਨ ਤੇ
a = 1, b = 5, c = – 1800
ਅਤੇ b² – 4ac = (5)² – 4 × 1 × (-1800)
= 25 + 7200
= 7225 > 0.

= 40 ਅਤੇ – 45
∴ ਕਿਸੇ ਰੇਲਗੱਡੀ ਦੀ ਚਾਲ ਰਿਣਾਤਮਕ ਨਹੀਂ ਹੋ ਸਕਦੀ
∴ਅਸੀਂ x = – 45 ਨੂੰ ਛੱਡ ਦਿੰਦੇ ਹਾਂ
∴ x = 40
∴ ਰੇਲਗੱਡੀ ਦੀ ਚਾਲ = 40 km/h

ਪ੍ਰਸ਼ਨ 9.
ਦੋ ਟੁੱਟੀਆਂ ਮਿਲਕੇ ਇੱਕ ਹੌਜ ਨੂੰ 9\(\frac{3}{8}\) ਘੰਟਿਆਂ ਵਿੱਚ ਭਰ ਸਕਦੀਆਂ ਹਨ । ਵੱਡੇ ਵਿਆਸ ਵਾਲੀ ਟੁੱਟੀ, ਘੱਟ ਵਿਆਸ ਵਾਲੀ ਟੁੱਟੀ ਤੋਂ 10 ਘੰਟੇ ਘੱਟ ਸਮਾਂ ਲੈਂਦੀ ਹੈ । ਹਰੇਕ ਟੁੱਟੀ ਦੁਆਰਾ ਹੌਜ਼ ਨੂੰ ਭਰਨ ਲਈ ਲਿਆ ਗਿਆ ਸਮਾਂ | ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਮੰਨ ਲਓ ਵੱਡੇ ਵਿਆਸ ਵਾਲੀ ਟੁੱਟੀ ਹੌਜ਼ ਭਰਨ ਵਿਚ ਜਿਨ੍ਹਾਂ ਸਮਾਂ ਲੈਂਦੀ ਹੈ = x
ਘੰਟੇ ਛੋਟੇ ਵਿਆਸ ਵਾਲੀ ਲੈਂਦੀ ਜਿਨ੍ਹਾਂ ਸਮਾਂ ਲੈਂਦੀ ਹੈ = (x + 10)
ਘੰਟੇ ਇੱਕ ਘੰਟੇ ਦੀ ਸਥਿਤੀ
ਵੱਡੀ ਟੁੱਟੀ ਹੌਜ਼ ਭਰ ਸਕਦੀ ਹੈ = \(\frac{1}{x+10}\)
∴ ਵੱਡੀ ਅਤੇ ਛੋਟੀ ਟੁੱਟੀ ਹੌਜ਼ ਭਰ ਸਕਦੀਆਂ ਹਨ
= \(\frac{1}{x}\) = \(\frac{1}{x+10}\) ….(1)
ਪਰ ਦੋਵੇਂ ਟੁੱਟੀਆਂ ਹੌਜ਼ ਭਰਨ ਵਿਚ ਜਿਨ੍ਹਾਂ ਸਮਾਂ ਲੈਣਗੀਆਂ
= 9\(\frac{3}{8}\) ਘੰਟੇ = \(\frac{75}{8}\) ਘੰਟੇ
ਹੁਣ ਦੋਵੇਂ ਟੁੱਟੀਆਂ ਇਕ ਘੰਟੇ ਵਿਚ ਹੌਜ਼ ਭਰ ਸਕਦੀਆਂ ਹਨ
= \(\frac{8}{75}\) …(2)
(1) ਅਤੇ (2) ਤੋਂ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ

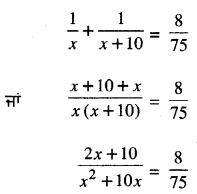
75 (2x + 10) = 8(x² + 10x)
150x + 750 = 8x² + 80x
ਜਾਂ 8x² + 80 – 150x – 750 = 0
8x² – 70x – 750 = 0
4x² – 35x – 375 = 0
ਇਸ ਦੀ ਤੁਲਨਾ ax² + bx + c = 0 ਨਾਲ ਕਰਨ ਤੇ ,
∴ a = 4, b = – 35, c = – 375
ਅਤੇ b² – 4ac = (-35)² –4 × 4 × (375)
= 1225 + 6000
= 7225 > 0

∵ ਸਮਾਂ ਰਿਣਾਤਮਕ ਨਹੀਂ ਹੋ ਸਕਦਾ ਹੈ
ਇਸ ਲਈ, ਅਸੀਂ x = \(\frac{-25}{4}\)ਨੂੰ ਛੱਡ ਦਿੰਦੇ ਹਾਂ
∴ x = 15
ਇਸ ਲਈ ਵੱਡੀ ਟੁੱਟੀ ਹੌਜ਼ ਭਰਨ ਵਿਚ ਸਮਾਂ ਲੈਂਦੀ ਹੈ = 15 ਘੰਟੇ
ਅਤੇ ਛੋਟੀ ਟੁੱਟੀ ਹੌਜ਼ ਭਰਨ ਵਿੱਚ ਸਮਾਂ ਲੈਂਦੀ ਹੈ
= (15 + 10) ਘੰਟੇ
= 25 ਘੰਟੇ

ਪ੍ਰਸ਼ਨ 10.
ਮੈਸਰ ਅਤੇ ਬੰਗਲੌਰ ਦੇ ਵਿਚਕਾਰ 132 km ਦਾ ਸਫ਼ਰ ਕਰਨ ਲਈ ਇਕ ਐਕਸਪ੍ਰੈੱਸ ਰੇਲਗੱਡੀ, ਸਵਾਰੀ ਗੱਡੀ ਤੋਂ 1 ਘੰਟਾ ਘੱਟ ਸਮਾਂ ਲੈਂਦੀ ਹੈ । ਵਿਚਕਾਰਲੇ ਸਟੇਸ਼ਨਾਂ ਤੇ ਰੁਕਣ ਦਾ ਸਮਾਂ ਧਿਆਨ ਵਿੱਚ ਨਾ ਰੱਖਿਆ । ਜਾਵੇ) ਜੇਕਰ ਐਕਸਪ੍ਰੈਸ ਰੇਲਗੱਡੀ ਦੀ ਔਸਤ ਚਾਲ, ਸਵਾਰੀ ਗੱਡੀ ਦੀ ਔਸਤ ਚਾਲ ਤੋਂ 11 km/h ਜ਼ਿਆਦਾ ਹੋਵੇ ਤਾਂ ਦੋਵੇਂ ਰੇਲਗੱਡੀਆਂ ਦੀ ਔਸਤ ਚਾਲ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਮੰਨ ਲਓ ਸਵਾਰੀ ਗੱਡੀ ਦੀ ਔਸਤ ਚਾਲ
= x km/h
ਐਕਸਪ੍ਰੈੱਸ ਰੇਲਗੱਡੀ ਦੀ ਔਸਤ ਚਾਲ
= (x + 11) km/h
ਮੈਸੂਰ ਅਤੇ ਬੰਗਲੌਰ ਵਿਚ ਦੂਰੀ
= 132 ਕਿ.ਮੀ.
ਸਵਾਰੀ ਗੱਡੀ ਦੁਆਰਾ ਲਿਆ ਸਮਾਂ = \(\frac{132}{x}\) ਘੰਟੇ

1452 = x² + 11x
ਜਾਂ x² + 11x – 1452 = 0
ਇਸ ਦੀ ਤੁਲਨਾ ax² + bx + c = 0 ਨਾਲ ਕਰਨ ਤੇ
∴ a = 1, b = 11, c = – 1452
ਅਤੇ b² – 4ac = (11)² – 4 × 1 × (- 1452)
= 121 + 5808
= 5929 > 0

= \(\frac{66}{2}\) ਅਤੇ \(\frac{-88}{2}\)
= 33, – 44
∵ ਰੇਲਗੱਡੀ ਦੀ ਚਾਲ ਰਿਣਾਤਮਕ ਨਹੀਂ ਹੋ ਸਕਦੀ
∴ x = 33
∴ ਸਵਾਰੀ ਗੱਡੀ ਦੀ ਔਸਤ ਚਾਲ
= 33 km/h.
ਅਤੇ ਐਕਸਪ੍ਰੈੱਸ ਰੇਲਗੱਡੀ ਦੀ ਔਸਤ ਚਾਲ
= (33 + 11) km/h
= 44 km/h

ਪ੍ਰਸ਼ਨ 11.
ਦੋ ਵਰਗਾਂ ਦੇ ਖੇਤਰਫਲਾਂ ਦਾ ਜੋੜ 48 m² ਹੈ । ਜੇਕਰ ਉਨ੍ਹਾਂ ਦੇ ਪਰਿਮਾਪਾਂ ਦਾ ਅੰਤਰ 24 m ਹੋਵੇ ਤਾਂ ਦੋਵੇਂ ਵਰਗਾਂ ਦੀਆਂ ਭੁਜਾਵਾਂ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਪਹਿਲਾਂ ਵੱਡੇ ਵਰਗ ਦੀ ਸਥਿਤੀ ਵਿਚ
ਮੰਨ ਲਓ ਵਰਗ ਦੀ ਹਰੇਕ ਭੁਜਾ ਦੀ ਲੰਬਾਈ = x m
ਵਰਗ ਦਾ ਖੇਤਰਫਲ = x² m²
ਵਰਗ ਦਾ ਪਰਿਮਾਪ = 4x m
ਛੋਟੇ ਵਰਗ ਦੀ ਸਥਿਤੀ ਵਿੱਚ
ਮੰਨ ਲਓ ਵਰਗ ਦੀ ਹਰੇਕ ਭੁਜਾ ਦੀ ਲੰਬਾਈ
= y m
ਵਰਗ ਦਾ ਖੇਤਰਫਲ = y²
ਵਰਗ ਦਾ ਪਰਿਮਾਪ = 4y m
ਪਹਿਲੀ ਸ਼ਰਤ ਅਨੁਸਾਰ,
x² + y² = 468 …(1)
ਦੂਸਰੀ ਸ਼ਰਤ ਅਨੁਸਾਰ,
4x – 4y = 24
4(x – y) = 24
x – y = 6
ਜਾਂ x = 6 + y ….(2)
(1) ਅਤੇ (2) ਤੋਂ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ।
(6 + y)² + y² = 468
36 + y² + 12y + y² = 468
2y² + 12y + 36 – 468 = 0
2y² + 12y – 432 = 0
y² + 6y – 216 = 0
ਇਸ ਦੀ ਤੁਲਨਾ ay² + by + c = 0 ਨਾਲ ਕਰਨ ਤੇ
∴ a = 1, b = 6, c = – 216
ਅਤੇ b² – 4ac = (6)² – 4 × 1 × (216)
= 36 + 864
= 900 > 0

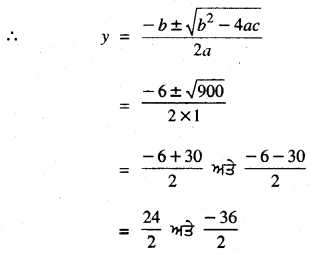
= 12 ਅਤੇ – 18
∵ ਵਰਗ ਦੀ ਭੁਜਾ ਰਿਣਾਤਮਕ ਨਹੀਂ ਹੋ ਸਕਦੀ
∴ ਅਸੀਂ y = – 18 ਨੂੰ ਛੱਡ ਦਿੰਦੇ ਹਾਂ
∴ y = 12
(2) ਤੋਂ, x = 6 + 12 = 18
∴ ਦੋਵੇਂ ਵਰਗਾਂ ਦੀਆਂ ਭੁਜਾਵਾਂ
12 m ਅਤੇ 18 m ਹਨ ।