Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 4 ਦੋ ਘਾਤੀ ਸਮੀਕਰਣ Ex 4.4 Textbook Exercise Questions and Answers.
PSEB Solutions for Class 10 Maths Chapter 4 ਦੋ ਘਾਤੀ ਸਮੀਕਰਣ Exercise 4.4
1. ਹੇਠਾਂ ਦਿੱਤੇ ਦੋ ਘਾਤੀ ਸਮੀਕਰਣਾਂ ਦੇ ਮੂਲਾਂ ਦੀ ਪ੍ਰਕ੍ਰਿਤੀ ਪਤਾ ਲਗਾਉ । ਜੇਕਰ ਮੂਲ ਸੰਭਵ ਹੋਣ ਤਾਂ ਉਨ੍ਹਾਂ ਦਾ ਪਤਾ ਲਗਾਉ ।
ਪ੍ਰਸ਼ਨ (i).
2x2 – 3x + 5 = 0
ਉੱਤਰ:
ਦਿੱਤੀ ਗਈ ਦੋ ਘਾਤੀ ਸਮੀਕਰਣ ਹੈ।
2x2 – 3x + 5 = 0
ਇਸ ਦੀ ਤੁਲਨਾ ax2 + bx + c = 0 ਨਾਲ ਕਰਨ ਤੇ
∴ a = 2, b = – 3, c = 5
D = b2 – 4ac
= (-3)2 – 4 × 2 × 5
= 9 – 40
= – 31 < 0
∴ ਦਿੱਤੀ ਹੋਈ ਦੋ ਘਾਤੀ ਸਮੀਕਰਣ ਦਾ ਕੋਈ ਵਾਸਤਵਿਕ ਮੂਲ ਨਹੀਂ ਹੈ ।
ਪ੍ਰਸ਼ਨ (ii).
3x2 – 4\(\sqrt {3}\) x + 4 = 0
ਉੱਤਰ:
ਦਿੱਤੀ ਗਈ ਦੋ ਘਾਤੀ ਸਮੀਕਰਣ ਹੈ
3x2 – 4\(\sqrt {3}\)x + 4 = 0
ਇਸ ਦੀ ਤੁਲਨਾ ax2 + bx + c = 0 ਨਾਲ ਕਰਨ ‘ਤੇ
∴ a = 3, b = -4\(\sqrt {3}\), c = 4
D = b2 – 4ac
= (-4\(\sqrt {3}\)x)2 -4 x 3 x 4
= 48 – 48 = 0
∴ ਦਿੱਤੀ ਹੋਈ ਸਮੀਕਰਣ ਦੇ ਵਾਸਤਵਿਕ ਅਤੇ ਬਰਾਬਰ ਮੂਲ ਹਨ ।

∴ ਦਿੱਤੀ ਹੋਈ ਦੋ ਘਾਤੀ ਸਮੀਕਰਣ ਦੇ ਮੂਲ ਹਨ \(\frac{2}{\sqrt{3}}\) ਅਤੇ \(\frac{2}{\sqrt{3}}\)
![]()
ਪ੍ਰਸ਼ਨ (iii).
2x2 – 6x + 3 = 0
ਉੱਤਰ:
ਦਿੱਤੀ ਹੋਈ ਦੋ ਘਾਤੀ ਸਮੀਕਰਣ ਹੈ
2x2 – 6x + 3 = 0
ਇਸ ਦੀ ਤੁਲਨਾ ax2 + bx + c = 0 ਨਾਲ ਕਰਨ ‘ਤੇ
∴ a = 2, b = – 6, c = 3
D = b2 – 4ac
= (-6)2 – 4 × 2 × 3
= 36 – 24
= 12 > 0
∴ ਦਿੱਤੀ ਹੋਈ ਦੋ ਘਾਤੀ ਸਮੀਕਰਣ ਦੇ ਵਾਸਤਵਿਕ ਨੂੰ ਅਤੇ ਅਲਗ-ਅਲਗ ਮੂਲ ਹਨ :
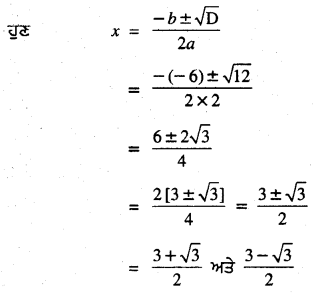
∴ ਦਿੱਤੀ ਹੋਈ ਦੋ ਘਾਤੀ ਸਮੀਕਰਣ ਦੇ ਮੂਲ \(\frac{3+\sqrt{3}}{2}\) ਅਤੇ \(\frac{3-\sqrt{3}}{2}\) ਹਨ ।
2. ਹੇਠਾਂ ਦਿੱਤੇ ਹਰੇਕ ਦੋ ਘਾਤੀ ਸਮੀਕਰਣ ਵਿਚ k ਦਾ ਅਜਿਹਾ ਮੁੱਲ ਪਤਾ ਕਰੋ ਕਿ ਉਸ ਦੇ ਦੋ ਬਰਾਬਰ ਮੂਲ ਹੋਣ :
ਪ੍ਰਸ਼ਨ (i).
2x2 + kx + 3 = 0
ਉੱਤਰ:
ਦਿੱਤੀ ਹੋਈ ਦੋ ਘਾਤੀ ਸਮੀਕਰਣ ਹੈ
2x2 + kx + 3 = 0
ਇਸ ਦੀ ਤੁਲਨਾ ax2 + bx + c = 0 ਨਾਲ ਕਰਨ ਤੇ
∴ a = 2, b = k, c = 3
∵ ਦਿੱਤੀ ਹੋਈ ਦੋ ਘਾਤੀ ਸਮੀਕਰਣ ਦੇ ਮੂਲ ਹਨ
∴ D = 0
b2 – 4ac = 0
(k)2 – 4 × 2 × 3 = 0
k2 – 24 = 0 .
k2 = 24
k2 = ±\(\sqrt {24}\)
k = ±2\(\sqrt {6}\)
![]()
ਪ੍ਰਸ਼ਨ (ii).
kx (x – 2) + 6 = 0.
ਉੱਤਰ:
ਦਿੱਤੀ ਹੋਈ ਦੋ ਘਾਤੀ ਸਮੀਕਰਣ ਹੈ
kx(x – 2) + 6 = 0
kx2 – 2kx + 6 = 0
ਇਸਦੀ ਤੁਲਨਾ ax2 + bx + c = 0 ਨਾਲ ਕਰਨ ਤੇ
∴ a = k, b = -2k, c = 6
∵ ਦਿੱਤੀ ਹੋਈ ਦੋ ਘਾਤੀ ਸਮੀਕਰਣ ਦੇ ਮੂਲ ਬਰਾਬਰ | ਹਨ।
∴ D = 0
b2 – 4ac = 0
(-2k)2 – 4 × k × 6 = 0
4k2 – 24k = 0
4k [k – 6] = 0
ਭਾਵ 4k = 0 ਜਾਂ k – 6 = 0
k = 0 ਜਾਂ . k = 6
∴ k = 0, 6
ਪ੍ਰਸ਼ਨ 3.
ਕੀ ਅਜਿਹਾ ਅੰਬਾਂ ਦਾ ਆਇਤਾਕਾਰ ਬਾਗ ਲਗਾਉਣਾ | ਸੰਭਵ ਹੈ ਜਿਸਦੀ ਲੰਬਾਈ, ਚੌੜਾਈ ਤੋਂ ਦੁੱਗਣੀ ਹੋਵੇ ਅਤੇ ਇਸਦਾ ਖੇਤਰਫਲ 800 m ਹੋਵੇ । ਜੇਕਰ ਸੰਭਵ ਹੈ ਤਾਂ ਇਸਦੀ ਲੰਬਾਈ ਅਤੇ ਚੌੜਾਈ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਮੰਨ ਲਓ ਆਇਤਾਕਾਰ ਬਾਗ ਦੀ ਲੰਬਾਈ = x m
ਅਤੇ ਆਇਤਾਕਾਰ ਬਾਗ ਦੀ ਚੌੜਾਈ = 2x m
ਆਇਤਾਕਾਰ ਬਾਗ ਦਾ ਖੇਤਰਫਲ = ਲੰਬਾਈ × ਚੌੜਾਈ
= [x × 2x] ਮੀ.2
= 2x2 ਮੀ.2
ਪ੍ਰਸ਼ਨ ਦੇ ਅਨੁਸਾਰ,
2x2 = 800
x2 = \(\frac{800}{2}\) = 400
x = ±\(\sqrt {400}\)
x = ±20
∵ ਬਾਗ਼ ਦੀ ਲੰਬਾਈ ਰਿਣਾਤਮਕ ਨਹੀਂ ਹੋ ਸਕਦੀ ।
∴ ਅਸੀਂ x = 20 ਨੂੰ ਛੱਡ ਦਿੰਦੇ ਹਾਂ ।
∴ x = 20
∴ ਬਾਗ਼ ਦੀ ਚੌੜਾਈ = 20 m
ਬਾਗ਼ ਦੀ ਲੰਬਾਈ
= (2 × 20) m = 40 m
![]()
ਪ੍ਰਸ਼ਨ 4.
ਕੀ ਹੇਠਾਂ ਦਿੱਤੀ ਸਥਿਤੀ ਸੰਭਵ ਹੈ । ਜੇਕਰ ਹਾਂ ਤਾਂ ਉਨ੍ਹਾਂ ਦੀ ਵਰਤਮਾਨ ਉਮਰਾਂ ਪਤਾ ਕਰੋ । ਦੋ ਮਿੱਤਰਾਂ ਦੀਆਂ ਉਮਰਾਂ ਦਾ ਜੋੜ 20 ਸਾਲ ਹੈ । ਚਾਰ ਸਾਲ ਪਹਿਲਾਂ ਉਨ੍ਹਾਂ ਦੀਆਂ ਉਮਰਾਂ ਸਾਲਾਂ ਵਿੱਚ) ਦਾ ਗੁਣਨਫਲ 48 ਸੀ ।
ਹੱਲ:
ਮੰਨ ਲਓ ਪਹਿਲੇ ਮਿੱਤਰ ਦੀ ਉਮਰ = x ਸਾਲ
ਦੂਸਰੇ ਮਿੱਤਰ ਦੀ ਉਮਰ = (20 – x) ਸਾਲ
ਚਾਰ ਸਾਲ ਪਹਿਲਾਂ :
ਪਹਿਲੇ ਮਿੱਤਰ ਦੀ ਉਮਰ = (x – 4) ਸਾਲ
ਦੂਸਰੇ ਮਿੱਤਰ ਦੀ ਉਮਰ = (20 – x – 4) ਸਾਲ
= (16 – x) ਸਾਲ
ਉਨ੍ਹਾਂ ਦਾ ਗੁਣਨਫਲ = (x – 4) (16 – x)
= 16x – x2 – 64 + 4x
= -x2 + 20x – 64
ਪ੍ਰਸ਼ਨੇ ਅਨੁਸਾਰ,
-x2 + 20x – 64 = 48
-x2 + 20x – 64 – 48 = 0
-x2 + 20x – 112 = 0
x2 – 20x + 12 = 0 …(1)
ਇਸ ਦੀ ਤੁਲਨਾ ax2 + bx + c = 0 ਨਾਲ ਕਰਨ ਤੇ
a = 1, b = – 20, c = 112
D = b2 – 4ac
= (-20)2 – 4 × 1 × 112
= 400 – 448
= – 48 < 0
∵ ਮੂਲ ਵਾਸਤਵਿਕ ਨਹੀਂ ਹਨ
∴ ਦਾ ਕੋਈ ਮੁੱਲ ਦੋ ਘਾਤੀ ਸਮੀਕਰਣ (1) ਨੂੰ ਸੰਤੁਸ਼ਟ ਨਹੀਂ ਕਰਦਾ ਹੈ
∴ ਦਿੱਤੀ ਹੋਈ ਸਥਿਤੀ ਸੰਭਵ ਨਹੀਂ ਹੈ ।
![]()
ਪ੍ਰਸ਼ਨ 5.
ਕੀ ਪਰਿਮਾਪ 80 m ਅਤੇ ਖੇਤਰਫਲ 400 m2 ਦੇ ਇੱਕ ਪਾਰਕ ਨੂੰ ਬਣਾਉਣਾ ਸੰਭਵ ਹੈ ? ਜੇਕਰ ਹੈ ਤਾਂ ਉਸਦੀ ਲੰਬਾਈ, ਚੌੜਾਈ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਮੰਨ ਲਓ ਆਇਤਾਕਾਰ ਪਾਰਕ ਦੀ ਲੰਬਾਈ = x ਮੀ.
ਆਇਤਾਕਾਰ ਪਾਰਕ ਦੀ ਚੌੜਾਈ = y ਮੀ.
∴ ਆਇਤਾਕਾਰ ਪਾਰਕ ਦਾ ਪਰਿਮਾਪ =2 (x + y) ਮੀ.
∴ ਆਇਤਾਕਾਰ ਪਾਰਕ ਦਾ ਖੇਤਰਫਲ = xy ਮੀ.2
ਪਹਿਲੀ ਸ਼ਰਤ ਅਨੁਸਾਰ
2 (x + y) = 80
x + y = \(\frac{80}{2}\) = 40
y = 40 – x …(1)
ਦੂਸਰੀ ਸ਼ਰਤ ਅਨੁਸਾਰ
xy = 400
x(40 – x) = 400 [(1) ਦਾ ਪ੍ਰਯੋਗ ਕਰਨ ਤੇ]
ਜਾਂ 40x – x2 = 400
ਜਾਂ 40x – x2 – 400 = 0
ਜਾਂ x2 – 40x + 400 = 0
ਇਸ ਦੀ ਤੁਲਨਾ ax2 + b + c = 0 ਨਾਲ ਕਰਨ ਤੇ
∴ a = 1, b = -40, c = 400
D = b2 – 4ac
= (-40)2 – 4 × 1 × 400
= 1600 – 1600 = 0

ਹੁਣ x = 20, ਤਾਂ (1) ਤੋਂ
y = 40 – 20 = 20
∴ ਆਇਤਾਕਾਰ ਪਾਰਕ ਦੀ ਲੰਬਾਈ ਅਤੇ ਚੌੜਾਈ ਦਾ | ਮਾਪ 20 m ਬਰਾਬਰ ਹੈ ।
∴ ਆਇਤਾਕਾਰ ਪਾਰਕ ਸੰਭਵ ਹੈ । ਇਹ ਵਰਗ ਹੈ ।
