Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 5 Arithmetic Progressions Ex 5.2 Textbook Exercise Questions and Answers.
PSEB Solutions for Class 10 Maths Chapter 5 Arithmetic Progressions Ex 5.2
Question 1
Fill in the blanks in the following table, given that a is the first term, d the common difference and a the nth term of the
AP:
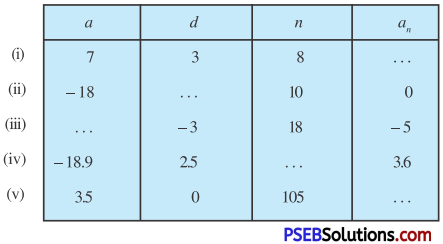
Solution:
(i) Here a = 7, d = 3, n = 8
∵ an = a + (n – 1)d
∴ a8 = 7 + (8 – 1)3
= 7 + 21 = 28.
(ii) Here a = – 18, n = 10, an = 0
∵ an = a + (n – 1)d
∴ a10 = – 18 + (10 – 1)d
or 0 = – 18 + 9d .
or 9d = 18
d = \(\frac{18}{2}\) = 2.
![]()
(iii) Here d = – 3, n = 18, an = – 5
∵ an = a + (n – 1)d
∴ a18 = a + (18 – 1)(-3)
or -5 = a – 51
or a = – 5 + 51 = 46.
(iv) Here a = – 18.9, d = 2.5 an = 3.6
∵ an = a + (n – 1)d
∴ 3.6 = – 18.9 + (n – 1) 2.5
or 3.6 + 18.9 = (n – 1) 2.5
or (n – 1) 2.5 = 22.5
or n – 1 = \(\frac{22.5}{2.5}\)
or n = 9 + 1 = 10.
(v) Here a = 3.5, d = 0, n = 105
∵ an = a + (n – 1) d
∴ an = 3.5 + (105 – 1) 0
an = 3.5 + 0 = 3.5.
Question 2.
Choose the correct choice in the following and justify:
(i) 30th term of the AP: 10, 7, 4, …………….. is
(A) 97 (B) 77 (C) – 77 (D) – 87
(ii) 11th term of the AP: – 3, – \(\frac{1}{2}\), 2, ………. is
(A) 28 (B) 22 (C) – 38 (D) – 48\(\frac{1}{2}\)
Solution:
(i) Given A.P. is 10, 7, 4 ……………
T1 = 10, T2 = 7, T3 = 4
T2 – T1 = 7 – 10 = – 3
T3 – T2 = 4 – 7 = – 3
∵ T2 – T1 = T3 – T2 = – 3 = d(say)
∵ Tn = a + (n – 1) d
Now, T30 = 10 + (30 – 1)(-3)
= 10 – 87 = – 77
∴ Correct choice is (C).
![]()
(ii) Given A.P. is – 3, –\(\frac{1}{2}\), 2, ……….
T1 = – 3 T2 = –\(\frac{1}{2}\), T3 = 2, …………..
T2 – T1 = –\(\frac{1}{2}\) + 3 = \(\frac{-1+6}{2}=\frac{5}{2}\)
T3 – T2 = 2 + \(\frac{1}{2}\) = \(\frac{4+1}{2}=\frac{5}{2}\)
∵ T2 – T1 = T3 – T2 = \(\frac{5}{2}\) = d(say)
∵ Tn = a + (n – 1) d
Now, T11 = -3 + (11 – 1) \(\frac{5}{2}\)
= -3 + 10 × \(\frac{5}{2}\) = – 3 + 25 = 22
∴ Correct choice is (B).
Question 3.
In the following APs, find the missing terms in the boxes:
(i) 2, ![]() , 26
, 26
(ii)![]() , 13,
, 13, ![]() , 3
, 3
(iii) 5,![]() ,
, ![]() , 9
, 9
(iv) – 4, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , 6
, 6
(v) ![]() , 38,
, 38, ![]() ,
, ![]() ,
, ![]() , – 22
, – 22
Solution:
Let a be the first term and ‘d’ be the common difference of given A.P.
(i) Here T1 = a = 2
and T3 = a + 2d = 26
or 2 + 2d = 26
or 2d = 26 – 2 = 24
or d = 12
∴ Missing term = T2 = a + d = 2 + 12 = 14.
![]()
(ii) Here, T2 = a + d = 13 ……………(1)
and T4 = a + 3d = 3 …………….(3)
Now, (2) – (1) gives
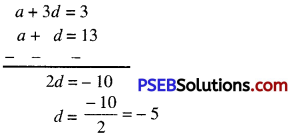
Substitute this value of d in (1), we get
a – 5 = 13
a = 13 + 5 = 18.
∴ T1 = a = 18
T3 = a + 2d = 18 + 2(-5)
= 18 – 10 = 8.
(iii)Here T1 = a = 5
and T4 = a + 3d = 9
or a + 3d = \(\frac{19}{2}\)
or 5 + 3d = \(\frac{19}{2}\)
or 3d = \(\frac{19}{2}\) – 5
or 3d = \(\frac{19-10}{2}=\frac{9}{2}\)
or d = \(\frac{9}{2} \times \frac{1}{3}=\frac{3}{2}\)
T2 = a + d = 5 + \(\frac{3}{2}\)
= \(\frac{10+3}{2}=\frac{13}{2}\)
T3 = a + 2d = 5 + 2(\(\frac{3}{2}\)) = 5 + 3 = 8.
(iv) Here T1 = a = —
T6 = a + 5d = 6
or -4 + 5d = 6
or 5d = 6 + 4
or 5d = 10
or d = \(\frac{10}{2}\) = 2
Now, T2 = a + d = -4 + 2 = -2
T3 = a + 2d = – 4 + 2(2)
= – 4 + 4 = 0
T4 = a + 3d = – 4 + 3(2)
= – 4 + 6 = 2
T5 = a + 4d = – 4 + 4(2)
= – 4 + 8 = 4
(v) Here T2 = a + d = 38 ………….(1)
and T6 = a + 5d = -22 ……………(2)
Now, (2) – (1) gives
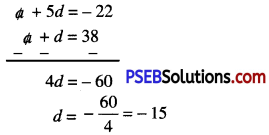
Substitute this value of d in (1), we get
a + (-15) = 38
a = 38 + 15 = 53
∴ T1 = a = 53
T3 = a + 2d = 53 + 2(-15) = 53 – 30 = 23.
T4 = a + 3d = 53 + 3(-15) = 53 – 45 = 8
T5 = a + 4d = 53 + 4(-15) = 53 – 60 = – 7.
![]()
Question 4
Which term of the A.P. 3, 8, 13, 18, …………… is 78?
Solution:
Given A.P. is 3, 8, 13, 18, ………….
T1 = 3, T2 = 8, T3 = 13, T4 = 18
T2 – T1 =8 – 3=5
T3 – T2= 13 – 8=5
T2 – T1 = T3 – T,= 5 = d (say)
Using, Tn = a + (n – I) d
or 78 = 3 + (n – 1) 5
or 5(n – 1) = 78 – 3 = 75
or n – 1 = 15
or n = 15 + 1 = 16
Hence, 16th term of given AP. is 78.
Question 5.
Find the number of terms in each of the following APs:
(i) 7, 13, 19,…, 205
(ii) 18, 15\(\frac{1}{2}\), 13, ………….., – 47
Solution:
(i) Given A.P. is 7, 13, 19, …………..
T1 = 7, T2 = 13, T3 = 19
T2 – T1 = 13 – 7 = 6
T3 – T2 = 19 – 13 = 6
T2 – T1 = T3 – T2 = 6 = d(say)
Using formula, Tn = a + (n – 1) d
205 = 7 + (n – 1) 6
or (n – 1) 6 = 205 – 7 = 198
or (n – 1) = \(\frac{198}{6}\)
or n – 1 = 33
n = 33 + 1 = 34
Hence, 34th term of an AP. is 205.
![]()
(ii) Given A P. is 18, 15\(\frac{1}{2}\), 13, …………..
T1 = 18, T2 = 15\(\frac{1}{2}\) = \(\frac{31}{2}\), T3 = 13
T2 – T1 = \(\frac{31}{2}\) – 18 = \(\frac{31-36}{2}=-\frac{5}{2}\)
T3 – T2 = 13 – \(\frac{31}{2}\) = \(\frac{26-31}{2}=-\frac{5}{2}\)
∵ T2 – T1 = T3 – T2 = \(\frac{-5}{2}\) = d (say)
Using formula. Tn = a + (n – 1) d
– 47 = 18 + (n – 1) \(\frac{-5}{2}\)
or (n – 1) (\(\frac{-5}{2}\)) = – 47 – 18
or (n – 1) (\(\frac{-5}{2}\)) = – 65
or n – 1 = – 65 × – \(\frac{2}{5}\)
or n – 1 = 26
or n = 26 + 1 = 27
Hence, 27th term of an A.P. is – 47.
Question 6.
Is – 150 a term of 11, 8, 5, 2….? why?
Solution:
Given sequence is 11, 8, 5, 2, ………..
T1 = 11, T2 = 8, T3 = 5, T4 = 2
T2 – T1 = 8 – 11 = – 3
T3 – T2 = 5 – 8 = – 3
T4 – T3 = 2 – 5 = – 3
T2 – T1 = T3 – T2 = T4 – T3 = – 3 = d (say).
Let – 150 be any term of given A.P.
then Tn = – 150
a+(n – 1)d = – 150
or 11 +(n – 1)(- 3) = – 150
or (n – 1)( – 3) = – 150 – 11 = – 161
or n – 1 = \(\frac{161}{3}\)
or n = \(\frac{161}{3}\) + 1 = \(\frac{161+3}{3}\)
n = \(\frac{164}{3}\) = 54\(\frac{2}{3}\),
which is not a natural number.
Hence, – 150 cannot be a term of given A.P.
![]()
Question 7.
Find the 31st term of an AP whose 11th term is 38 and 16th term is 73.
Solution:
Let ‘a’ and 4d’ be the first term and common difference of given A.P.
Given that T11 = 38
a +(11 – 1) d = 38
[∵ Tn = a + (n – 1) d]
a + 10 d = 38
and T16 = 73
a + (16 – 1) d = 73
[∵ Tn = a + (n – 1) d]
a + 15 d = 73
Now, (2) – (1) gives
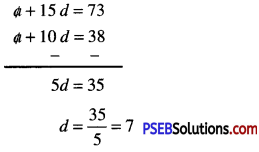
Substitute this value of d in (1), we get
a + 10 (7) = 38
or a + 70 = 38
or a = 38 – 70 = – 32
Now, T31 = a + (31 – 1) d
= – 32 + 30 (7) = – 32 + 210 = 178.
Question 8.
An AP consists of 50 terms of which 3rd term is 12 and the last term is 106. Find the 291h term.
Solution:
Let ‘a’ and ‘d’ be the first term and common difference of given A.P.
Given that, T3 = 12
a + (3 – 1) d = 12
∵ Tn = a + (n – 1) d
or a + 2d = 12 ………………(1)
and Last term = T50 = 106
a + (50 – 1) d = 106
∵ Tn = a + (n – 1) d
a + 49 d = 106 ……………(2)
Now, (2) – (1) gives

Substitute this value of d in (1), we get
a + 2(2) = 12
or a + 4 = 12
or a + 12 – 4 = 8
Now, T29 = a + (29 – 1) d
= 8 + 28 (2) = 8 + 56 = 64.
![]()
Question 9.
If the 3rd and 9th tenus of an A.P. are 4 and – 8 respectively, which term of this A.P. is zero.
Solution:
Let ‘a’ and ‘d’ be the first term and common difference of given AP.
Given that: T3 = 4
a + (3 – 1) d = 4
∵ Tn = a + (n – 1) d
a + 2d = 4 …………..(1)
and T9 = – 8
a + (9 – 1) d = 8
and T9 = – 8
a + (9 – 1)d = 8
∵ Tn = a + (n – 1) d
or a + 8d = – 8
Now, (2) – (1) gives
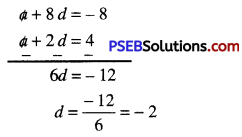
Substitute this value of d in (1), we get
a + 2(- 2) = 4
or a – 4 = 4
or a = 4 + 4 = 8
Now, Tn = 0 (Given)
a + (n – 1) d = 0
or 8 + (n – 1)(- 2)=0
or -2 (n – 1) = – 8
or n – 1 = 4
or n = 4 + 1 = 5
Hence, 5th term of an AP. is zero.
Question 10.
The 17th term of an A.P. exceeds its 10th term by 7. Find the common difference.
Solution:
Let ‘a’ and ‘d’ be the first term and common difference of given A.P.
Now, T17 = a + (17 – 1) d = a + 16 d
and T10 = a + (10 – 1) d = a + 9 d
According to question
T17 – T10 = 7
(a + 16 d) – (a + 9 d) = 7
or a + 16 d – a – 9 d = 7
7 d = 7
or d = \(\frac{7}{7}\) = 1
Hence, common difference is 1.
![]()
Question 11.
Which term of the A.P. 3, 15, 27, 39, …………. will be 132 more than its 54th term?
Solution:
Let ‘a’ and ‘d’ be the first term and common difference of given A.P.
Given A.P. is 3, 15, 27, 39, …
T1 = 3, T2 = 15, T3 = 27, T4 = 39
T2 – T1 = 15 – 3 = 12
T3 – T2 = 27 – 15 = 12
:. d=T2 – T1 = T3 – T2 =12
Now, T54 = a + (54 – 1) d
= 3 + 53 (12) = 3 + 636 = 639
According to question
T = T54 + 132
a + (n – 1)d = 639 + 132
3 + (n – 1)(12) = 771
(n – 1) 12 = 771 – 3 = 768
or n – 1 = \(\frac{768}{12}\) = 64
or n = 64 + 1 = 65
Hence, 65th term of A.P. is 132 more than its 54th term.
Question 12.
Two APs have the same common difference. The difference between their 100th terms is 100, what is the difference between their 1000th terms?
Solution:
Let ‘a’ and ‘d’ be the first term and common difference of first AP.
Also, ‘A’ and ‘d’ be the first term and common difference of second A.P.
According to question
[T100 of second A.P.] – [T100 of first A.P.] = 100
or[A +(100 – 1)d] – [a +(100 – 1)d] = 100
or A + 99d – a – 99d = 100
or A – a = 100
Now, [T1000 of second A.P.] – [T1000 of first A.P.]
= [A + (1000 – 1) d) – (a + (1000 – 1) d]
= A + 999 d – a – 999 d
= A – a = 100 [Using (I)].
![]()
Question 13.
How many three-digits numbers are divisible by 7?
Solution:
Three digits numbers which divisible by 7 are 105, 112, 119 , 994
Here a = T1 = 105, T2 = 112, T3 = 119 and Tn = 994
T2 – T1 = 112 – 105=7
T3 – T2 = 119 – 112=7
∴ d = T2 – T1 = T3 – T2 = 7
Given that, Tn = 994
a + (n – 1) d = 994
or 105 + (n – 1) 7 = 994
or (n – 1) 7 = 994 – 105
or (n – 1) 7 = 889
or n – 1 = \(\frac{889}{7}\) = 127
or n = 127 + 1 = 128.
Hence, 128 terms of three digit number are divisible by 7.
Question 14.
How many multiples of 411e between 10 and 250?
Solution:
Multiples of 4 lie between 10 and 250 are 12, 16, 20, 24, … 248
Here a = T1 = 12, T2 = 16, T3 = 20 and Tn = 248
T2 – T1 = 16 – 12 = 4
T3 – T2 = 20 – 16 = 4
∴ d = T2 – T1 = T3 – T2 = 4
Given that, Tn = 248
a + (n – 1) d = 248
or 12 + (n – 1)4 = 248
or 4(n – 1) = 248 – 12 = 236
or n – 1 = \(\frac{236}{4}\) = 59
or n = 59 + 1 = 60
Hence, there are 60 terms which are multiples of 4 lies between 10 and 250.
![]()
Question 15.
For what value of n, are the n terms of two A.P.s 63, 65, 67, …………. and 3, 10, 17, …………….. equal?
Solution:
Given A.P. is 63, 65, 67, ……………..
Here a = T1 = 63, T2 = 65, T3 = 67
T2 – T1 = 65 – 63 = 2
T3 – T2 = 67 – 65 = 2
∴ d = T2 – T1 = T3 – T2 = 2
and second A.P. is 3, 10, 17, …
Here a = T1 = 3, T2 = 10, T3 = 17
T2 – T1 = 10 – 3 = 7
T3 – T2 = 17 – 10 = 7
According to question.
[nth term of first A.P.] = [nth term of second A.P.]
63 + (n – 1)2 = 3 + (n – 1) 7
or 63 + 2n – 2 = 3 + 7n – 7
or 61 + 2n = 7n – 4
or 2n – 7n = – 4 – 61
– 5n = – 65
n = \(\frac{65}{5}\) = 13.
Question 16.
Determine the AP. whose third term is 16 and 7 term exceeds the by 12.
Solution:
Let ‘a’ and ‘d’ be the first term and common difference of given A.P.
Given that T3 = 16
a + (3 – 1) d = 16
a + 2d = 16
According to question
T7 – T5 = 12
[a + (7 – 1) d] – [a + (5 -1) d] = 12
a + 6 d – a – 44 = 12
2d = 12
d = \(\frac{12}{2}\) = 6
Substitute this value of d in (1), we get
a + 2(6) = 16
a = 16 – 12 = 4 .
Hence, given A.P. are 4, 10, 16, 22, 28, ………….
![]()
Question 17.
Find the 20th term from the last term of the AP: 3, 8, 13, ………., 253.
Solution:
Given A.P. is 3, 8, 13, …………., 253
Here, a = T1 = 3, T2 = 8, T3 =13 and Tn = 253
T2 – T1 = 8 – 3 = 5
T3 – T2 = 13 – 8 = 5
∴ d = T2 – T1 = T3 – T1 = 5
Now, Tn = 253
3 + (n – 1)5 = 253
∵ Tn = a + (n – 1) d
(n – 1) 5 = 250
n-1 = \(\frac{250}{5}\) = 50
n = 50 + 1 = 51
20th term from the end of AP = (Total number of terms) – 20 + 1
= 51 – 20 + 1 = 32nd term
∴ 20th term from the end of AP
= 32nd term from the starting
= 3 + (32 – 1)5
∵ Tn = a + (n – 1)d
= 3 + 31 × 5
= 3 + 155 = 158.
Question 18.
The sum of the 4th and 8th term of an AP is 24 and the sum of the 6’ and 10th terms is 44. FInd the first three terms of the A.P.
Solution:
Let ‘a’ and ‘d’ be the first term and common difference of given A.P.
According to 1st condition
T4 + T8 = 24
a + (4 – 1) d + a + (8 – 1) d = 24
∵ Tn = a + (n – 1) d
or 2a + 3d + 7d = 24
2a + 10d = 24
a + 5d = 12 …………(1)
According to 2nd condition
T6 + T10 = 44
a + (6 – 1) d + a +(10 – 1) d = 44
∵ Tn = a + (n – 1) d
2a + 5d + 9d = 44
2a + 14d = 44
a + 7d = 22
Now (2) – (1) gives
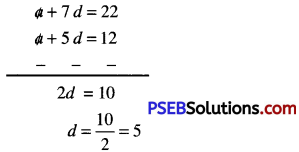
Substitute this value of d in (I). we get
a + 5(5) = 12
a + 25 = 12
a = 12 – 25 = -13
T1 = a = -13
T2 = a + d = 13 + 5 = -8
T2 = a + 2d = – 13 + 2(5) = – 13 + 10 = -3
Hence, given A.P. is -13, -8, -3, ……………
![]()
Question 19.
Subba Rao started work in 1995 at an annual salary of ₹ 5000 and received an increment of ₹ 200 each year. In which year did his income reach ₹ 7000?
Solution:
Subba Rao’s starting salary = ₹ 5000
Annual increment = ₹ 200
Let ‘n’ denotes number of years.
∴ first term = a = ₹ 5000
Common diflerence = d = ₹ 200
and Tn = ₹ 7000
5000 + (n – 1) 200 = 7000
∵ Tn = a + (n – 1) d
(n – 1) 200 = 7000 – 5000
or (n – 1) 200 = 2000
or n – 1 = \(\frac{2000}{200}\) = 10
or n = 10 + 1 = 11
Now, in case of year the sequence are 1995. 1996, 1997, 1998, ……………
Here a = 1995, d = 1 and n = 11
Let Tn denotes the required year.
∴ Tn = 1995 + (11 – 1) 1
= 1995 + 10 = 2005
Hence, in 2005, Subba Rao’s salary becomes 7000.
![]()
Question 20.
Ramkali saved ₹ 5 in the first week of a year and then increased her weekly saving by ₹ 1.75. If in the nth week, her weekly saving becomes ₹ 20.75, find n.
Solution:
Amount saved in first week = ₹ 5
Increment in saving every week = ₹ 1.75
It is clear that, it form an A.P. whose terms are
T1 = 5, d = 1.75
∴ T2 = 5 + 1.75 = 6.75
T3 = 6.75 + 1.75 = 8.50
Also. Tn = 20. 75 (Given)
5 + (n – 1) 1.75 = 20.75
∵ Tn = a + (n – 1) d
or (n – 1) 1.75 = 20.75 – 5
or (n – 1) 1.75 = 15.75
or (n – 1) = \(\frac{1575}{100} \times \frac{100}{175}\)
or n – 1 = 9
or n = 9 + 1 = 10
Hence, in 10th week, Ramkali’s saving becomes ₹ 20.75.
