Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 5 Arithmetic Progressions Ex 5.4 Textbook Exercise Questions and Answers.
PSEB Solutions for Class 10 Maths Chapter 5 Arithmetic Progressions Ex 5.4
Question 1.
Which term of the A.P. 121, 117, 113, …………. is its first negative term?
Solution:
Given A.P is 121, 117, 113, …
Here a = T1 = 121 ;T2 = 117; T3 = 113
d = T2 – T1 = 117 – 121 = – 4
Using formula, Tn = a + (n – 1) d
Tn = 121 + (n – 1) (- 4)
= 121 – 4n + 4
= 125 – 4n.
According to question :—
Tn < 0
or 125 – 4n < 0
or 125 < 4n or 4n > 125.
or n > \(\frac{125}{4}\)
or n > 31\(\frac{1}{4}\).
But n must be integer, for first negative term.
∴ n = 32.
Hence, 32nd term be the first negative term of given A.P.
![]()
Question 2.
The sum of the third and the seventh term of an A.P. is 6 and their product ¡s 8. Find the sum of first sixteer
terms of an A.P.
Solution:
Let ‘a’ and ‘d’ be the first term and common diftèrence of given A.P.
According to 1st condition
T3 + T7 = 6
[a + (3 – 1)d] + [a + (7 – 1) d] = 6
∵ [Tn = a + (n – 1) d]
or a + 2d + a + 6d = 6
or 2a + 8d = 6
or a + 4d = 3 …………….(1)
According to 2nd condition
T3 (T7) = 8
[a + (3 – 1) d] [a + (7 – 1)d] = 8
∵ [Tn = a + (n – 1) d]
or (a + 2d) (a + 6d) = 8
or [3 – 4d + 2d] [3 – 4d + 6d] = 8
[Using (1), a = 3 – 4d]
or (3 – 2d) (3 + 2d) = 8
or 9 – 4d2 = 8
or 4d2 = 98
or d2 = \(\frac{1}{4}\)
d = ± \(\frac{1}{2}\)
![]()
Case I:
When d = \(\frac{1}{2}\)
Putting d = \(\frac{1}{2}\) in (1), we get:
a + 4 (\(\frac{1}{2}\)) = 3
or a + 2 = 3
or a = 3 – 2 = 1
Using formula, Sn = \(\frac{n}{2}\) [2a + (n – 1) d]
S16 = \(\frac{16}{2}\) [2 (1) + (16 – 1) \(\frac{1}{2}\)].
Case II:
Putting d = – \(\frac{1}{2}\) in (1), we get,
When d = – \(\frac{1}{2}\)
a + 4 (-\(\frac{1}{2}\)) = 3
a – 2 = 3
or a = 3 + 2 = 5
Using formula,
Sn = \(\frac{n}{2}\) [2a + (n – 1)d]
S16 = \(\frac{16}{2}\) [2(5) + (16 – 1) (-\(\frac{1}{2}\))]
= 8[10 – \(\frac{15}{2}\)]
= 8 \(\left[\frac{20-15}{2}=\frac{5}{2}\right]\)
S16 = 20.
![]()
Question 3.
A ladder has rungs 25 cm apart (see fig.) The rungs decrease uniformly in length from 45 cm at the bottom to 25 cm at the top. If the top and bottom rungs are 2 latex]\frac{1}{2}[/latex] m apart, what is the length of the wood required for the rungs?
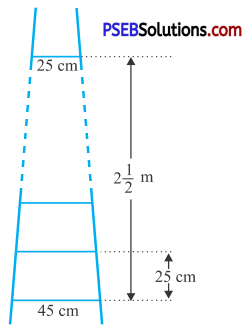
[Hint: Number of rungs = \(\frac{250}{25}\) + 1]
Solution:
Total length of rungs = 2 \(\frac{1}{2}\) m = \(\frac{5}{2}\) m
= (\(\frac{5}{2}\) × 100) cm = 250 cm
Length of each rung = 25 cm
∴ Number of rungs = \(\frac{\text { Total length of rungs }}{\text { Length of each rung }}\) + 1
= \(\frac{250}{25}\) + 1 = 10 + 1 = 11
Length of first rung =45 cm
Here a = 45; l = 25; n = 11
Length of the wood for rungs
= S11
= \(\frac{n}{2}\) [a + l]
= \(\frac{11}{2}\) [45 + 25]
= \(\frac{1}{2}\) × 70
= 11 × 35 = 385
Hence, length of the wood for rungs has 385 cm.
![]()
Question 4.
The houses of a row are numbered consecutively from 1 to 49. Show that there is a value of x such that the sum of the numbers of the houses preceding the house numbered x is equal to the sum of the numbers of the houses following it and find this value of x.
[Hint: Sx – 1 = S49 – S1]
Solution:
Let ‘x’ denotes the number of any house.
Here a = T1 = 1 ;d = 1
According to question,
Sx – 1 = S49 – Sx
= \(\frac{x-1}{2}\) [2 (1) + (x – 1 – 1) (1)]
= \(\frac{49}{2}\) [1 + 49] – \(\frac{x}{2}\) [2 (1) + (x – 1) (1)]
[Using Sn = \(\frac{n}{2}\) [2a + (n – 1) d] and Sn = \(\frac{n}{2}\) (a + l) ]
or \(\frac{x-1}{2}\) [2 + x – 2] = \(\frac{49}{2}\) (50) – \(\frac{x}{2}\) [2 + x – 1]
or \(\frac{x(x-1)}{2}=49(25)-\frac{x(x+1)}{2}\)
or \(\frac{x}{2}\) [x – 1 + x + 1] = 1225
\(\frac{x}{2}\) × 2x = 1225
or x2 = 1225
or x = 35.
![]()
Question 5.
A small terrace at a football ground comprises of 15 step each of which is 50 m long and built of solid concrete. Each step has a rise of \(\frac{1}{4}\) m and a tread of \(\frac{1}{2}\) m (see fig.) Calculate the total volume of concrete required to build the terrace.
[Hint: Volume of concrete required to build of the first step \(\frac{1}{4}\) × \(\frac{1}{2}\) × 50 m3].

Solution:
Volume of concrete required to build the first step \(\frac{1}{4}\) × \(\frac{1}{2}\) × 50 m3]
= [latex]\frac{25}{4}[/latex] m3
Volume of concrete required to build the second step = [\(\frac{25}{4}\) × \(\frac{1}{2}\) × 50] m3
= \(\frac{75}{2}\) m3
Volume of concrete required to build the third step = [\(\frac{3}{4}\) × \(\frac{1}{2}\) × 50] m3 and so on upto 15 steps.
Here a = T1 = \(\frac{25}{4}\);
T2 = \(\frac{25}{2}\);
T3 = \(\frac{75}{4}\); and n = 15.
d = T2 – T1 = \(\frac{25}{2}\) – \(\frac{25}{4}\)
= \(\frac{50-25}{4}\) = \(\frac{25}{4}\).
Total volume of concrete required to buld the terrace = S15
= \(\frac{n}{2}\) [2a + (n – 1)d]
= \(\frac{15}{2}\left[2\left(\frac{25}{4}\right)+(15-1) \frac{25}{4}\right]\)
= \(\left[\frac{25}{4} \times \frac{14 \times 25}{4}\right]\)
= \(\frac{15}{2}\left[\frac{25}{2} \times \frac{175}{2}\right]\)
= \(\frac{15}{2} \times \frac{200}{2}\) = 750
Hence, total volume of concrete required to build the terrace is 750 m3.
