PSEB 10th Class Maths Solutions Chapter 5 ਅੰਕਗਣਿਤਕ ਲੜੀਆਂ Ex 5.4

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 5 ਅੰਕਗਣਿਤਕ ਲੜੀਆਂ Ex 5.4 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 10 Maths Chapter 5 ਅੰਕਗਣਿਤਕ ਲੜੀਆਂ Exercise 5.4

ਪ੍ਰਸ਼ਨ 1.
A.P. : 121, 117, 113, … ਦਾ ਕਿਹੜਾ ਸਭ ਤੋਂ ਪਹਿਲਾ ਰਿਣਾਤਮਕ ਪਦ ਹੋਵੇਗਾ ?
ਸਿੰਕੇਤ : a_n < 0 ਦੇ ਲਈ 1 ਪਤਾ ਕਰੋ ।
ਹਲ:
ਦਿੱਤੀ ਹੋਈ A.P. ਹੈ ।
121, 117, 113, …
ਇੱਥੇ a = T₁ = 121 ; T₂ = 117; T₃ = 113
d = T₂ = T₁ = 117 – 121 = -4
ਸੂਤਰ T_n = a + (n – 1) d ਦਾ ਪ੍ਰਯੋਗ ਕਰਨ ਤੇ
T_n = 121 + (n – 1) (-4)
= 121 – 4n + 4
= 125 – 4n
ਪ੍ਰਸ਼ਨ ਅਨੁਸਾਰ
T_n < 0
125 – 4n < 0 4n > 125
n > \(\frac{125}{4}\)
n > 31\(\frac{1}{4}\)
ਪਰ ਪਹਿਲੇ ਰਿਣਾਤਮਕ ਪਦ ਲਈ n ਸੰਪੂਰਨ ਸੰਖਿਆ ਹੋਣੀ ਚਾਹੀਦੀ ਹੈ।
∴ n = 32
∴ ਦਿੱਤੀ ਗਈ A.P. ਦਾ 32ਵਾਂ ਪਦ ਪਹਿਲਾ ਰਿਣਾਤਮਕ ਪਦ ਹੋਵੇਗਾ ।

ਪ੍ਰਸ਼ਨ 2.
ਕਿਸੇ A.P. ਦੇ ਤੀਸਰੇ ਅਤੇ ਸੱਤਵੇਂ ਪਦਾਂ ਦਾ ਜੋੜ 6 ਹੈ ਅਤੇ ਉਨ੍ਹਾਂ ਦਾ ਗੁਣਨਫਲ 8 ਹੈ । ਇਸ A.P. ਦੇ ਪਹਿਲੇ 16 ਪਦਾਂ ਦਾ ਜੋੜਫਲ ਪਤਾ ਕਰੋ ।
ਹਲ:
ਮੰਨ ਲਉ ‘a’ ਅਤੇ ‘d’ ਦਿੱਤੀ ਹੋਈ A.P. ਦਾ ਪਹਿਲਾ ਪਦ ਅਤੇ ਸਾਂਝਾ ਅੰਤਰ ਹੈ ।
ਪਹਿਲੀ ਸ਼ਰਤ ਅਨੁਸਾਰ,
T₃ + T₇ = 6
[a + (3 – 1)d] + [a + (7 – 1) d] = 6
|∵ T_n = a + (n – 1)d
a + 2d + a + 6d = 6
2a + 8d = 6
a + 4d = 3 …(1)
ਦੂਸਰੀ ਸ਼ਰਤ ਅਨੁਸਾਰ,
T₃(T₇) = 8
[a + (3 – 1) d] [a + (7 – 1) d] = 8
|∵ T_n = a + (n – 1) d
(a + 2d) (a + 6d) = 8
[3 – 4d + 2] [3 – 4d + 6d] = 8
[(1) ਤੋਂ a = 3 – 4d]
(3 – 2d) (3 + 2d) = 8
9 – 4d² = 8
4d² =9 – 8
d² = \(\frac{1}{4}\)
d = ±\(\frac{1}{2}\)
ਸਥਿਤੀ I. ਜਦੋਂ d = \(\frac{1}{2}\)
d = \(\frac{1}{2}\) ਦਾ ਮੁੱਲ (1) ਵਿਚ ਰੱਖਣ ‘ਤੇ ਮਿਲਦਾ ਹੈ
a + 4\(\left(\frac{1}{2}\right)\) = 3
a + 2 = 3
a = 3 – 2 = 1
ਸੂਤਰ ਦਾ ਪ੍ਰਯੋਗ ਕਰਕੇ \(\frac{n}{2}\) = [2a + (n – 1) d]
S_n = \(\frac{16}{2}\)[2(1) + (16 – 1)\(\frac{1}{2}\)]
= 8[2 + \(\frac{15}{2}\)]
= 8[latex]\frac{4+15}{2}[/latex]
= 8 × \(\frac{19}{2}\)
S₁₆ = 76.
ਸਥਿਤੀ II. ਜਦੋਂ ਵੀ d = \(-\frac{1}{2}\)
d = \(-\frac{1}{2}\) ਦਾ ਮੁੱਲ (1) ਵਿਚ ਰੱਖਣ ‘ਤੇ

S₁₆ = 20.

ਪ੍ਰਸ਼ਨ 3.
ਇੱਕ ਪੌੜੀ ਦੇ ਲਗਾਤਾਰ ਡੰਡੇ ਆਪਸ ਵਿੱਚ 25 cm ਦੀ ਦੂਰੀ ‘ਤੇ ਹਨ (ਦੇਖੋ ਚਿੱਤਰ ( ਡੰਡਿਆਂ ਦੀ ਲੰਬਾਈ ਇਕ ਸਮਾਨ ਰੂਪ ਨਾਲ ਘੱਟਦੀ ਜਾਂਦੀ ਹੈ ਅਤੇ ਸਭ ਤੋਂ ਹੇਠਲੇ ਡੰਡੇ ਦੀ ਲੰਬਾਈ 45 cm ਅਤੇ ਸਭ ਤੋਂ ਉਪਰਲੇ ਡੰਡੇ ਦੀ ਲੰਬਾਈ 25 cm ਹੈ । ਜੇਕਰ ਉਪਰਲੇ ਅਤੇ ਹੇਠਲੇ ਡੰਡੇ ਦੇ ਵਿਚਕਾਰਲੀ ਦੂਰੀ 2\(\frac{1}{2}\) m ਹੈ ਤਾਂ ਡੰਡਿਆਂ ਨੂੰ ਬਣਾਉਣ ਲਈ ਲੱਕੜੀ ਦੀ ਕਿੰਨੀ ਲੰਬਾਈ ਦੀ ਲੋੜ ਹੋਵੇਗੀ ?

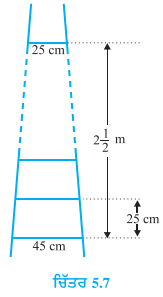
ਸੰਕੇਤ : ਡੰਡਿਆਂ ਦੀ ਸੰਖਿਆਂ = \(\frac{250}{25}\) + 1 ਹੈ ।
ਹਲ:
ਡੰਡਿਆਂ ਵਿਚਕਾਰਲੀ ਕੁਲ ਲੰਬਾਈ
= 2\(\frac{1}{2}\)m = \(\frac{5}{2}\)m
= (\(\frac{5}{2}\) × 100)m
= 250 cm
ਹਰੇਕ ਡੰਡੇ ਦੀ ਲੰਬਾਈ = 25 cm

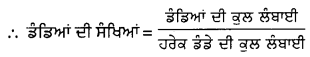
= \(\frac{250}{25}\) = 10
ਪਹਿਲੇ ਡੰਡੇ ਦੀ ਲੰਬਾਈ = 45 cm
ਇੱਥੇ a = 45; l = 25 ; n = 10
ਡੰਡਿਆਂ ਦੇ ਲਈ ਲਕੜੀ ਦੀ ਲੰਬਾਈ = S₁₀
= \(\frac{n}{2}\)[a + l]
= \(\frac{10}{2}\)[45 + 25]
= 5 (70)
= 350.
ਡੰਡਿਆਂ ਲਈ ਲੋੜੀਂਦੀ ਲਕੜੀ ਦੀ ਲੰਬਾਈ 350 cm ਹੈ ।

ਪ੍ਰਸ਼ਨ 4.
ਇਕ ਕਤਾਰ ਵਿੱਚ ਮਕਾਨਾਂ ਨੂੰ ਲਗਾਤਾਰ ਸੰਖਿਆਂ ਤੋਂ 49 ਨਾਲ ਦਰਸਾਇਆ ਗਿਆ ਹੈ । ਦਿਖਾਉ ਕਿ 1 ਦਾ ਇੱਕ ਅਜਿਹਾ ਮੁੱਲ ਹੈ ਕਿ x ਨਾਲ ਦਰਸਾਏ ਮਕਾਨ ਤੋਂ ਪਹਿਲੇ ਦੇ ਮਕਾਨਾਂ ਦੀ ਸੰਖਿਆਵਾਂ ਦਾ ਜੋੜ ਉਸ ਤੋਂ ਬਾਅਦ ਵਾਲੇ ਮਕਾਨਾਂ ਦੀ ਸੰਖਿਆਵਾਂ ਦੇ ਜੋੜ ਦੇ ਬਰਾਬਰ ਹੈ । ਦਾ ਮੁੱਲ ਪਤਾ ਕਰੋ । | [ਸੰਕੇਤ : S_x-1= S₄₉ – S_x ਹੈ ]
ਹਲ:
ਮੰਨ ਲਉ x’ ਕਿਸੇ ਮਕਾਨ ਦੀ ਸੰਖਿਆਂ ਨੂੰ ਦਰਸਾਉਂਦਾ ਹੈ ।
ਇੱਥ a = T₁ = 1; d = 1
ਪ੍ਰਸ਼ਨ ਅਨੁਸਾਰ
S_x-1 = S₄₉ – S_x
= \(\frac{x-1}{2}\)[2(1) + (x – 1 – 1) (1)]
= \(\frac{49}{2}\)[1 + 49] – \(\frac{x}{2}\)[2 (1) + (x -1)(1)]
[ਸੂਤਰ S_n = \(\frac{n}{2}\)[2a + (n – 1)d]
ਅਤੇ \(\frac{n}{2}\)(a + l) ਦਾ ਪ੍ਰਯੋਗ ਕਰਕੇ

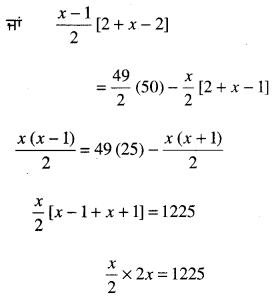
x² = 1225
x = 35

ਪ੍ਰਸ਼ਨ 5.
ਇੱਕ ਫੁੱਟਬਾਲ ਦੇ ਮੈਦਾਨ ਵਿਚ ਇੱਕ ਛੋਟਾ ਚਬੂਤਰਾ ਹੈ | ਜਿਸ ਵਿਚ 15 ਪੌੜੀਆਂ ਬਣੀਆਂ ਹੋਈਆਂ ਹਨ । ਇਨ੍ਹਾਂ ਪੌੜੀਆਂ ਵਿਚੋਂ ਹਰੇਕ ਦੀ ਲੰਬਾਈ 50 m ਹੈ ਅਤੇ ਠੋਸ ਕੰਕਰੀਟ ਦੀ ਬਣੀ ਹੋਈ ਹੈ । ਹਰੇਕ ਪੌੜੀ ਵਿੱਚ \(\frac{1}{4}\) m ਦੀ ਚੌੜਾਈ ਅਤੇ \(\frac{1}{2}\) m ਦਾ ਫੈਲਾਵ (ਚੌੜਾਈ) ਹੈ । (ਦੇਖੋ ਚਿੱਤਰ) । ਇਸ ਚਬੂਤਰੇ ਨੂੰ ਬਣਾਉਣ ਲਈ ਲੱਗੀ ਕੰਕਰੀਟ ਦਾ ਕੁਲ ਆਇਤਨ ਪਤਾ ਕਰੋ ।
[ਸੰਕੇਤ : ਪਹਿਲੀ ਪੌੜੀ ਨੂੰ ਬਣਾਉਣ ਲਈ ਲੱਗੀ ਕੰਕਰੀਟ ਦਾ ਆਇਤਨ \(\frac{1}{4}\) × \(\frac{1}{2}\) × 50 m²ਹੈ ॥]

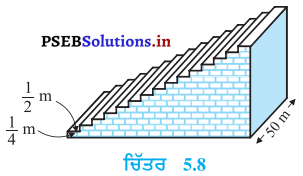
ਹੱਲ :
ਪਹਿਲੀ ਪੌੜੀ ਬਣਾਉਣ ਵਿਚ ਲੱਗੀ ਕੰਕਰੀਟ ਦਾ
ਆਇਤਨ = (\(\frac{1}{4}\) × \(\frac{1}{2}\) × 50) m³
= \(\left(\frac{25}{4}\right)\) m³
ਦੂਸਰੀ ਪੌੜੀ ਬਣਾਉਣ ਵਿਚ ਲੱਗੀ ਕੰਕ੍ਰਿਟ ਦਾ ਆਇਤਨ
= (\(\frac{2}{4}\) × \(\frac{1}{2}\) × 50) m³
= \(\left(\frac{25}{2}\right)\) m³
ਤੀਸਰੀ ਪੌੜੀ ਬਣਾਉਣ ਵਿਚ ਲੱਗੀ ਕੰਕਰੀਟ ਦਾ ਆਇਤਨ
= (\(\frac{3}{4}\) × \(\frac{1}{2}\) × 50) m³
= \(\left(\frac{75}{4}\right)\) m³
ਇਸੇ ਤਰ੍ਹਾਂ ਅੱਗੋਂ 15 ਪੌੜੀਆਂ ਹਨ ।

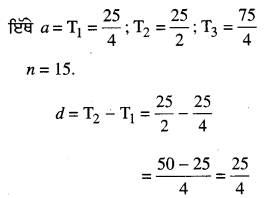
ਚਬੂਤਰਾ ਬਣਾਉਣ ਵਿਚ ਲੱਗੇ ਕੰਕਰੀਟ ਦਾ ਆਇਤਨ
= S₁₅

∴ ਚਬੂਤਰਾ ਬਣਾਉਣ ਲਈ ਲੋਂੜੀਦਾ ਦਾ ਕੰਕਰੀਟ = 750 m³