Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 6 त्रिभुज Ex 6.2 Textbook Exercise Questions and Answers
PSEB Solutions for Class 10 Maths Chapter 6 त्रिभुज Ex 6.2
प्रश्न 1.
आकृति (i) और (ii) में DE || BC है।
(i) में, EC और
(ii) में AD ज्ञात कीजिए :
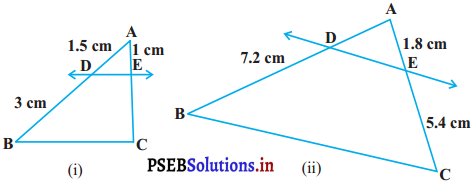
हल :
(i) ∆ABC में, DE || BC …………..(दिया है)
∴ \(\frac{\mathrm{AD}}{\mathrm{BD}}=\frac{\mathrm{AE}}{\mathrm{EC}}\)
[आधारभूत समानुपातिकता प्रमेय का प्रयोग करने पर]
\(\frac{1.5}{3}=\frac{1}{\mathrm{EC}}\)EC = \(\frac{3}{1.5}\)
EC = \(\frac{3 \times 10}{15}\) = 2 cm
∴ EC = 2 cm.
![]()
(ii) ∆ABC में,
DE || BC ……………(दिया है)
∴ \(\frac{A D}{B D}=\frac{A E}{E C}\)
[आधारभूत समानुपातिकता प्रमेय का प्रयोग करने पर]
\(\frac{\mathrm{AD}}{7.2}=\frac{1.8}{5.4}\)AD = \(\frac{1.8 \times 7.2}{5.4}\)
= \(\frac{1.8}{10} \times \frac{72}{10} \times \frac{10}{54}\)
= \(\frac{24}{10}\)
AD = 2.4
∴ AD = 2.4 cm.
![]()
प्रश्न 2.
किसी APQR की भुजाओं PQ और PR पर क्रमशः बिंदु E और F स्थित हैं। निम्नलिखित में से प्रत्येक स्थिति के लिए, बताइए कि क्या EF || QR है:
(i) PE = 3.9 cm, EQ = 3 cm, PF = 3.6 cm और FR = 2.4 cm
(ii) PE = 4 cm, QE = 4.5 cm, PF = 8 cm और RF = 9 cm.
(iii) PQ = 1.28 cm, PR=3D 2.56 cm, PE = 0.18 cm और PF = 0.36 cm.
हल :
∆PQR में दो बिंदु क्रमशः E और F भुजाओं PQ और PR पर स्थित हैं।
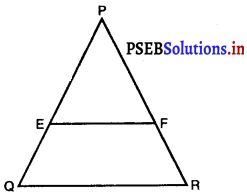
(i) PE = 3.9 cm, EQ = 3 cm, PF = 3.6 cm, FR = 2.4 cm
\(\frac{\mathrm{PE}}{\mathrm{EQ}}=\frac{3.9}{3}=\frac{39}{30}=\frac{13}{10}\) = 1.3
\(\frac{\mathrm{PF}}{\mathrm{FR}}=\frac{3.6}{2.4}=\frac{36}{24}=\frac{3}{2}\) = 1.5
\(\frac{P E}{E Q} \neq \frac{P F}{F R}\)∴ EF, QR के समांतर नहीं है। .
(ii) PE = 4 cm, QE = 4.5 cm, PF = 8 cm, RF = 9 cm.
\(\frac{\mathrm{PE}}{\mathrm{QE}}=\frac{4}{4.5}=\frac{40}{45}=\frac{8}{9}\) ……………(1)
\(\frac{\mathrm{PF}}{\mathrm{RF}}=\frac{8}{9}\) ……………(2)
(1) और (2) से,
\(\frac{\mathrm{PE}}{\mathrm{QE}}=\frac{\mathrm{PF}}{\mathrm{RF}}\)∴ आधारभूत समानुपातिकता प्रमेय के विलोम से EF || QR.
(iii) PQ = 1.28 cm, PR = 2.56 cm, PE = 0.18 cm, PF = 0.36 cm.
EQ = PQ – PE = 1.28 – 0.18 = 1.10 cm
ER = PR – PF = 2.56-0.36 = 2.20 cm
यहा \(\frac{\mathrm{PE}}{\mathrm{EQ}}=\frac{0.18}{1.10}=\frac{18}{110}=\frac{9}{55}\) …………….(1)
और \(\frac{\mathrm{PF}}{\mathrm{FR}}=\frac{0.36}{2.20}=\frac{36}{220}=\frac{9}{55}\) …………..(2)
(1) और (2) से
\(\frac{\mathrm{PE}}{\mathrm{EQ}}=\frac{\mathrm{PF}}{\mathrm{FR}}\)∴ आधारभूत समानुपातिकता प्रमेय के विलोम से EF || QR.
![]()
प्रश्न 3.
आकृति में यदि LM || CB और LN || CD हो, तो सिद्ध कीजिए कि है।
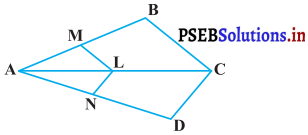
हल:
∆ABC में, LM || CB (दिया है)
∴ \(\frac{\mathrm{AM}}{\mathrm{MB}}=\frac{\mathrm{AL}}{\mathrm{LC}}\) ………….(1)
(आधारभूत समानुपातिकता प्रमेय से)
पुन: ∆ACD में,
LN || CD (दिया है)
∴ \(\frac{A N}{N D}=\frac{A L}{L C}\) ……………..(2) (आधारभूत समानुपातिकता प्रमेय से)
(1) और (2) से,
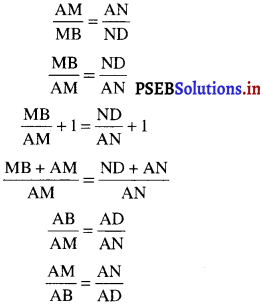
![]()
प्रश्न 4.
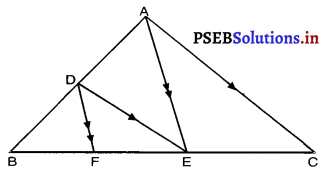
आकृति में DE || AC और DF || AE है। सिद्ध कीजिए कि \(\frac{\mathbf{B F}}{\mathbf{F E}}=\frac{\mathbf{B E}}{\mathbf{E C}}\) है।
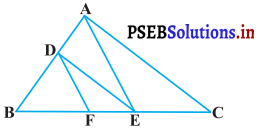
हल :
∆ABE में,
DE || AC (दिया है)
∴ \(\frac{\mathrm{BD}}{\mathrm{DA}}=\frac{\mathrm{BE}}{\mathrm{EC}}\) …………….(1)
[आधारभूत समानुपातिकता प्रमेय से]
∆ABE में, DF || AE
\(\frac{\mathrm{BD}}{\mathrm{DA}}=\frac{\mathrm{BF}}{\mathrm{EF}}\) …………..(2)
[आधारभूत समानुपातिकता प्रमेय से]
(1) और (2) से,
![]()
प्रश्न 5.
आकृति में DE || 0Q और DF || OR है। दर्शाइए कि EF || QR है।
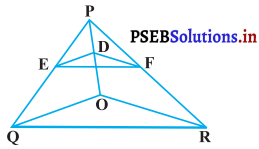
हल :
दिया है : ∆PQR में, DE || OQ, DF || QR.
सिद्ध करना है : EF || QR.
उपपत्ति : APQO में, ED || QO (दिया है)
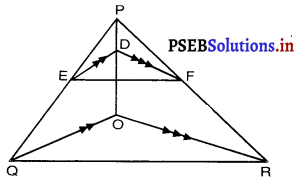
∴ \(\frac{\mathrm{PD}}{\mathrm{DO}}=\frac{\mathrm{PF}}{\mathrm{EQ}}\) …………..(1)
[आधारभूत समानुपातिकता प्रमेय से]
पुन: ∆POR में, DF || OR (दिया है)
∴ \(\frac{\mathrm{PD}}{\mathrm{DO}}=\frac{\mathrm{PE}}{\mathrm{FR}}\) ……………..(2)
[आधारभूत समानुपातिकता प्रमेय से]
(1) और (2) में,
∆PQR में, आधारभूत समानुपातिकता प्रमेय के विलोम से,
EF || QR.
![]()
प्रश्न 6.
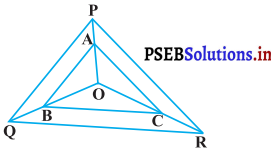
आकृति में क्रमशः OP, OQ और OR पर स्थित बिंदु A, B और C इस प्रकार हैं कि AB || PQ और AC || PR है। दर्शाइए कि BC || QR है।
हल :
दिया है : ∆PQR में बिंदु A, B और C क्रमशः OP, OQ और OR पर इस प्रकार स्थित हैं कि AB || PQ, AC || PR
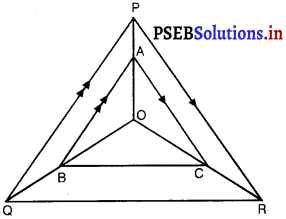
सिद्ध करना है : BC || QR.
उपपत्ति : ∆OPQ में, AB || PQ (दिया है)
∴ \(\frac{\mathrm{OA}}{\mathrm{AP}}=\frac{\mathrm{OB}}{\mathrm{BQ}}\) …………..(1)
[आधारभूत समानुपातिकता प्रमेय से
पुनः ∆OPR में, AC || PR (दिया है)
∴ \(\frac{\mathrm{OA}}{\mathrm{AP}}=\frac{\mathrm{OC}}{\mathrm{CR}}\) ……………(2)
[आधारभूत समानुपातिकता प्रमेय से]
(1) और (2) से,
∴ आधारभूत समानुपातिकता प्रमेय के विलोम से. ∆OQR में BC || QR है।
![]()
प्रश्न 7.
प्रमेय 6.1 का प्रयोग करते हुए सिद्ध कीजिए कि एक त्रिभुज की एक भुजा के मध्य-बिंदु से होकर दूसरी भुजा के समांतर खींची गई रेखा तीसरी भुजा को समद्विभाजित करती है।(याद कीजिए कि आप इसे IX में सिद्ध कर चुके हैं।)
हल :
दिया है : ∆ABC में, D, AB का मध्य बिंदु है अर्थात् AD = DB है।
BC के समांतर रेखा AC को E पर प्रतिच्छेद करती है जैसा कि आकृति में दिखाया गया है अर्थात् DE || BC है।
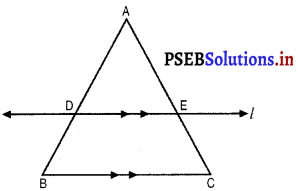
सिद्ध करना है : E, AC का मध्य-बिन्दु है।
उपपत्ति : D, AB का मध्य-बिन्दु है।
अर्थात् AD = DB (दिया है)
\(\frac{\mathrm{AD}}{\mathrm{BD}}\) ……………..(1)
पुन: ∆ABC में, DE || BC
∴ \(\frac{\mathrm{AD}}{\mathrm{DB}}=\frac{\mathrm{AE}}{\mathrm{EC}}\)
[आधारभूत समानुपातिकता प्रमेय से]
1 = \(\frac{\mathrm{AE}}{\mathrm{EC}}\) [(1) से]
∴ AE = EC
∴ E, AC का मध्य-बिंदु है।
![]()
प्रश्न 8.
प्रमेय 6.2 का प्रयोग करते हुए सिद्ध कीजिए कि एक त्रिभुज की किन्हीं दो भुजाओं के मध्य-बिन्दुओं को मिलाने वाली रेखा तीसरी भुजा के समांतर होती है (याद कीजिए कि आप कक्षा IX में ऐसा कर चुके हैं)।
हल :
दिया है : ∆ABC में, D और E क्रमश: AB और AC के मध्य-बिंदु हैं जिससे कि AD = BD और AE = EC हैं। D और E को मिलाया गया है।
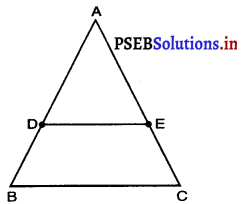
सिद्ध करना है : DE || BC
उपपत्ति: D, AB का मध्य बिंदु है।
अर्थात् AD = BD
\(\frac{\mathrm{AD}}{\mathrm{BD}}\) = 1 …………..(1)
E, AC का मध्य बिंदु है। (दिया है)
∴ AE = EC
\(\frac{\mathrm{AE}}{\mathrm{EC}}\) = 1 ………….(2)
(1) और (2) से
\(\frac{\mathrm{AB}}{\mathrm{BD}}=\frac{\mathrm{AE}}{\mathrm{EC}}\)आधारभूत समानुपातिकता प्रमेय के विलोम के प्रयोग से, DE || BC।
![]()
प्रश्न 9.
ABCD एक समलंब है जिसमें AB || DC है तथा इसके विकर्ण परस्पर बिंदु O पर प्रतिच्छेद करते है। दर्शनीय कि \(\frac{\mathrm{AO}}{\mathrm{BO}}=\frac{\mathrm{CO}}{\mathrm{DO}}\) है।
हल :
दिया है : ABCD एक समलंब है जिसमें AB || DC है। विकर्ण AC तथा BD परस्पर बिंदु पर प्रतिच्छेद करते हैं।
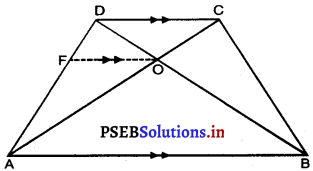
सिद्ध करना है: \(\frac{\mathrm{AO}}{\mathrm{BO}}=\frac{\mathrm{CO}}{\mathrm{DO}}\)
रचना : O में से FO || DC || AB खींचिए।
उपपत्ति : ∆DAB में,
FO || AB (रचना)
∴ \(\frac{D F}{F A}=\frac{D O}{B O}\) ……………(1)
[आधारभूत समानुपातिकता प्रमेय के प्रयोग से]
पुन: ∆DCA में, FO || DC (रचना)
\(\frac{\mathrm{DF}}{\mathrm{FA}}=\frac{\mathrm{CO}}{\mathrm{AO}}\) …………..(2)
[आधारभूत समानुपातिकता प्रमेय के प्रयोग से]
(1) और (2) से
\(\frac{\mathrm{DO}}{\mathrm{BO}}=\frac{\mathrm{CO}}{\mathrm{AO}}\)⇒ \(\frac{\mathrm{AO}}{\mathrm{BO}}=\frac{\mathrm{CO}}{\mathrm{DO}}\)
![]()
प्रश्न 10.
एक चतुर्भुज ABCD के विकर्ण परस्पर बिंदु O पर प्रतिच्छेद करते हैं कि \(\frac{\mathrm{AO}}{\mathrm{BO}}=\frac{\mathrm{CO}}{\mathrm{DO}}\) है। दर्शाइए कि ABCD एक समलंब है।
हल :
दिया है : चतुर्भुज ABCD में विकर्ण AC और BD परस्पर बिंदु 0 पर इस प्रकार प्रतिच्छेद करते हैं कि \(\frac{\mathrm{AO}}{\mathrm{BO}}=\frac{\mathrm{CO}}{\mathrm{DO}}\)
सिद्ध करना है : चतुर्भुज ABCD एक समलंब है।
रचना : ‘O’ में से रेखा EO || AB खींचिए, जो AD को E पर मिलती है।
उपपत्ति : ∆DAB में,
EO || AB
∴ \(\frac{\mathrm{DE}}{\mathrm{EA}}=\frac{\mathrm{DO}}{\mathrm{OB}}\) ………..(1)
[आधारभूत समानुपातता प्रमेय के प्रयोग से]

(1) और (2) से,
\(\frac{\mathrm{DE}}{\mathrm{EA}}=\frac{\mathrm{CO}}{\mathrm{AO}}\)∴ आधारभूत समानुपातिकता प्रमेय के प्रयोग से EO || DC
EO || AB
साथ ही, AB || DC
∴ चतुर्भुज ABCD एक समलंब है जिसमें AB || CD.
