PSEB 10th Class Maths Solutions Chapter 6 त्रिभुज Ex 6.3

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 6 त्रिभुज Ex 6.3 Textbook Exercise Questions and Answers

PSEB Solutions for Class 10 Maths Chapter 6 त्रिभुज Ex 6.3

प्रश्न 1.
बताइए कि आकृति में दिए त्रिभुजों के युग्मों में से कौन-कौन से युग्म समरूप हैं ? उस समरूपता कसौटी को लिखिए जिसका प्रयोग आपने उत्तर देने में किया है तथा साथ ही समरूप त्रिभुजों को सांकेतिक रूप में व्यक्त कीजिए।

(i)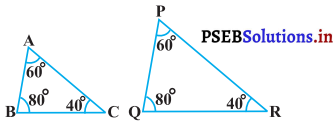

(ii)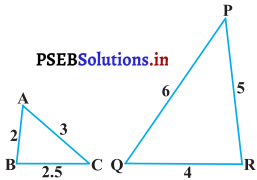

(iii)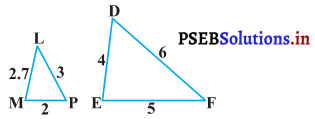

(iv)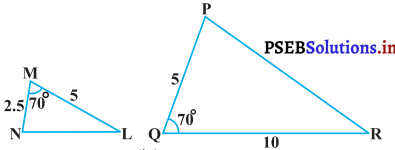

(v)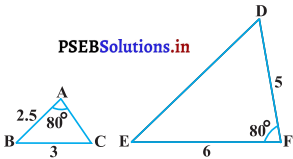

(vi)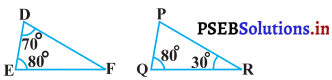

हल :
(i) ∆ABC तथा ∆PQR में,
∠A = ∠P (प्रत्येक 60°)
∠B = ∠Q (प्रत्येक 80°)
∠C = ∠R (प्रत्येक 40°)
∴ ∆ABC ~ ∆PQR [AAA समरूपता कसौटी)

(ii) ∆ABC तथा ∆PQR में,
\(\frac{\mathrm{AB}}{\mathrm{RQ}}=\frac{2}{4}=\frac{1}{2}\) ………….(1)

\(\frac{\mathrm{AC}}{\mathrm{PQ}}=\frac{3}{6}=\frac{1}{2}\) ………….(2)

\(\frac{\mathrm{AB}}{\mathrm{RQ}}=\frac{2.5}{5}=\frac{1}{2}\) ………….(3)
(1), (2) और (3) से,
\(\frac{\mathrm{BC}}{\mathrm{PR}}=\frac{\mathrm{AC}}{\mathrm{PQ}}=\frac{\mathrm{BC}}{\mathrm{PR}}=\frac{1}{2}\)
∴ ∆ABC ~ ∆QRP [SSS समरूपता कसौटी से)

(iii) ∆LMP तथा ∆DEF में,

\(\frac{\mathrm{MP}}{\mathrm{DE}}=\frac{2}{4}=\frac{1}{2}\) \(\frac{\mathrm{PL}}{\mathrm{DF}}=\frac{3}{6}=\frac{1}{2}\) \(\frac{\mathrm{LM}}{\mathrm{EF}}=\frac{2.7}{5}=\frac{27}{50}\)

यहाँ \(\frac{\mathrm{MP}}{\mathrm{DE}}=\frac{\mathrm{PL}}{\mathrm{DF}} \neq \frac{\mathrm{LM}}{\mathrm{EF}}\)
∴ दो त्रिभुजें समरूप नहीं हैं।

(iv) ∆MNL तथा ∆PQR में,
\(\frac{\mathrm{MP}}{\mathrm{QR}}=\frac{5}{10}=\frac{1}{2}\)

∠M = ∠Q (प्रत्येक 70°)

\(\frac{\mathrm{MN}}{\mathrm{PQ}}=\frac{3}{6}=\frac{1}{2}\)

∴ ∆MNL ~ ∆QPR [SAS समरूपता कसौटी से]

(v) ∆ABC और ∆DEF में,

\(\frac{\mathrm{AB}}{\mathrm{DF}}=\frac{2.5}{5}=\frac{1}{2}\) \(\frac{\mathrm{BC}}{\mathrm{EF}}=\frac{3}{6}=\frac{1}{2}\)

∠B ≠ ∠F
∴ ∆ABC तथा ∆DEF समरूप नहीं हैं।

(vi) ∆DEF में,
∠D = 70°, ∠E = 80°
∠D + ∠E + ∠F = 180°
70° + 80° + ∠F = 180°
∠F = 180° – 70° – 80°
∠F = 30°
∆PQR में,
∠Q = 80°, ∠R = 30°
∠P + ∠Q + ∠R = 180°
(त्रिभुज के कोणों का योगफल)
∠P + 80° + 30° = 180°
∠P = 180° – 80° – 30°
∠P = 70°
∆DEF तथा ∆PQR में,
∠D = ∠P (70° प्रत्येक)
∠E = ∠Q (80° प्रत्येक)
∠F = ∠R (30° प्रत्येक)
∴ ∆DEF ~ ∆PQR (AAA समरूपता कसौटी)

प्रश्न 2.
आकृति में, ∆ODC ~ ∆OBA, ∠BOC = 125° और ∠CDO = 70° है। ∠DOC, ∠DCO और ∠OAB ज्ञात कीजिए।

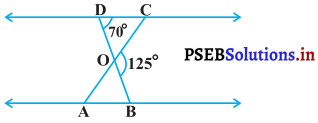
हल :
∠BOC = 125°
∠CDO = 70°
DOC एक सरल रेखा है।
∴ ∠DOC + ∠COB = 180°
∠DOC + 125 = 180°
∠DOC = 180° – 125°
∠DOC = 55°
∠DOC = ∠AOB = 55° [शीर्षाभिमुख कोण]
∆ODC ~ ∆OBA
∠D = ∠B = 70°
∆DOC में,
∠D + ∠O + ∠C = 180°
70° + 55° + ∠C = 180°
∠C = 180° – 70° – 550
∠C = 55°
∠C = ∠A = 55°
∠DOC = 55°
∠DCO = 55°
∠OAB = 55°

प्रश्न 3.
समलंब ABCD, में AB || DC है, के विकर्ण AC और BD परस्पर O परिच्छेद करते हैं। दो त्रिभुजों की समरूपता कसौटी का प्रयोग करते हुए, दर्शाइए कि \(\frac{\mathrm{OA}}{\mathrm{OC}}=\frac{\mathrm{OB}}{\mathrm{OD}}\) है।
हल :

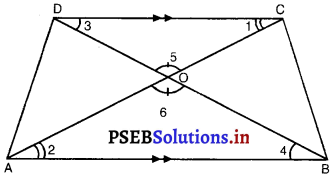
दिया है : समलंब ABCD जिसमें AB || CD है और विकर्ण AC तथा BD परस्पर O पर प्रतिच्छेद करते हैं।
सिद्ध करना है. \(\frac{\mathrm{OA}}{\mathrm{OC}}=\frac{\mathrm{OB}}{\mathrm{OD}}\)
AB || CD
उपपत्ति : AB || DC
∆DOC और ∆BOA में,
∠1 = ∠2 (एकांतर कोण)
∠5 = ∠6 (शीर्षाभिमुख कोण)
∠3 = ∠4 (एकांतर कोण) ..
∴ ∆DOC ~ ∆BOA [AAA समरूपता कसौटी]

\(\frac{\mathrm{DO}}{\mathrm{BO}}=\frac{\mathrm{OC}}{\mathrm{OA}}\) [यदि दो त्रिभुजें समरूप हों, तो संगत भुजाएँ समानुपाती होती हैं।} |

⇒ \(\frac{\mathrm{OA}}{\mathrm{OC}}=\frac{\mathrm{BO}}{\mathrm{DO}}\)

प्रश्न 4.
आकृति में, \(\frac{\mathrm{QR}}{\mathrm{QS}}=\frac{\mathrm{QT}}{\mathrm{PR}}\) तथा ∠1 = ∠2 है। दर्शाइए कि ∆PQS ~ ∆TQR है।
हल :
दिया है ∆TQR में
\(\frac{\mathrm{QR}}{\mathrm{QS}}=\frac{\mathrm{QT}}{\mathrm{PR}}\) तथा
∠1 = ∠2
सिद्ध करना है : ∆PQS ~ ∆TQR
उपपत्ति : ∆PQR में,
∠1 = ∠2 (दिया है)
∴ PR = PQ
[बराबर कोणों की सम्मुख भुजाएँ बराबर होती हैं।]

∠1 = ∠1 (उभयनिष्ठ)
∴ ∆PQS ~ ∆TQR [SAS समरूपता कसौटी]

प्रश्न 5.
∆PQR की भुजाओं PR और QR पर क्रमशः बिंदु S और T इस प्रकार स्थित हैं कि ∠P = ∠RTS है। दर्शाइए कि ∆RPQ ~ ∆RTS है।
हल :
दिया है :- ∆PQR की भुजाओं PR और QR पर क्रमश: बिंदु S और T इस प्रकार स्थित हैं कि ∠P = ∠RTS है।

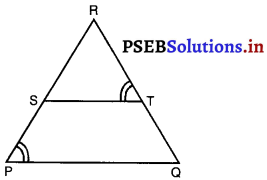
सिद्ध करना है : ∆RPQ ~ ∆RTS
उपपत्ति : ∆RPQ और ∆RTS में,
∠RPQ = ∠RTS (दिया है)
∠R = ∠R (उपनिष्ठ)
∆PQS ~ ∆TQR [AA समरूपता कसौटी]

प्रश्न 6.
आकृति में, यदि ∆ABE ≅ ∆ACD है, तो दर्शाइए कि ∆ADE ~ ∆ABC है।

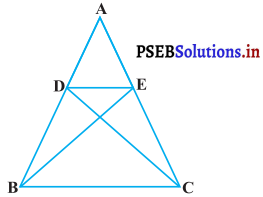
हल:
दिया है : ∆ABC और ∆ABE ≅ ∆ACD है।
सिद्ध करना है : ∆ADE ~ ∆ABC
उपपत्ति : ∆ABE = ∆ACD (दिया है)
AB = AC (सर्वांगसम त्रिभुजों के संगत भाग)
और AE = AD (सर्वांगसम त्रिभुजों के संगत भाग)
\(\frac{\mathrm{AB}}{\mathrm{AC}}\) = 1 ……………….(1)

\(\frac{\mathrm{AD}}{\mathrm{AE}}\) = 1 ………………(2)

(1) और (2) से, \(\frac{\mathrm{AB}}{\mathrm{AC}}=\frac{\mathrm{AD}}{\mathrm{AE}}\)

∆ADE और ∆ABC में, \(\frac{\mathrm{AD}}{\mathrm{AE}}=\frac{\mathrm{AB}}{\mathrm{AC}}\)
∠A = ∠A (उभयनिष्ठ)
∴ ∆ADE ~ ∆ABC [SAS समरूपता कसौटी से]

प्रश्न 7.
आकृति में, ∆ABC के शीर्षलंब AD और CE परस्पर बिंदु P पर प्रतिच्छेद करते हैं। दर्शाइए कि :
(i) ∆AEP ~ ∆CDP
(ii) ∆ABD ~ ∆CBE
(iii) ∆AEP ~ ∆ADB
(iv) ∆PDC ~ ∆BEC.
हल:
दिया है : ∆ABC, AD | BC

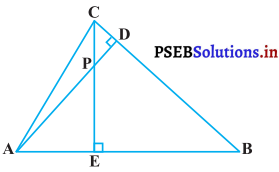
सिद्ध करना है:
(i) ∆AEP ~ ∆CDP
(ii) ∆ABD ~ ∆CBE
(iii) ∆AEP ~ ∆ADB
(iv) ∆PDC ~ ∆BEC.

उपपत्ति : (i) ∆AEP और ∆CDP में,
∠E = ∠D (प्रत्येक 90°)
∠APE = ∠CPD (शीर्षाभिमुख कोण)
∴ ∆AEP ~ ∆CDP [AA समरूपता कसौटी]

(ii) ∆ABD और ∆CBE में,
∠D = ∠E (प्रत्येक 90°)
∠B = ∠B (उभयनिष्ठ)
∴ ∆ABD ~ ∆CBE [AA समरूपता कसौटी]

(iii) ∆AEP और ∆ADB में,
∠E = ∠D (प्रत्येक 90°)
∠A = ∠A (उभयनिष्ठ)
∴ ∆AEP ~ ∆ADB [AA समरूपता कसौटी]

(vi) ∆PDC और ∆BEC में,
∠C = ∠C (उभयनिष्ठ)
∠D = ∠E (प्रत्येक 90°)
∴ ∆PDC ~ ∆BEC [AA समरूपता कसौटी]

प्रश्न 8.
समांतर चतुर्भुज ABCD की बढ़ाई गई भुजा AD पर स्थित E एक बिंदु है तथा BE भुजा CD को F पर प्रतिच्छेद करती है। दर्शाइए कि AABE ~ACFB

त्रिभुज
हल :
दिया है :- समांतर चतुर्भुज ABCD की बढ़ाई गई भुजा AD पर स्थित E एक बिंदु है तथा BE भुजा CD को F पर प्रतिच्छेद करती है।

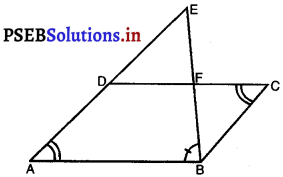
सिद्ध करना है : ∆ABE ~ ∆CFB
उपपत्ति : ∆ABE और ∆CFB में,
∠A = ∠C (II gm की सम्मुख भुजाएँ)
∠ABE = ∠CFB (एकांतर कोण)
∴ ∆ABE ~ ∆CFB (AA समरूपता कसौटी)

प्रश्न 9.
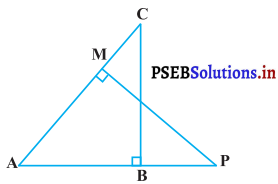
आकृति में, ABC और AMP दो समकोण त्रिभुज हैं, जिनके कोण B और M समकोण हैं। सिद्ध कीजिए कि
(i) ∆ABC ~ ∆AMP
(ii) \(\frac{\mathbf{C A}}{\mathbf{P A}}=\frac{\mathbf{B C}}{\mathbf{M P}}\)

हल :
दिया है : ∆ABC और ∆AMP दो समकोण त्रिभुज हैं, जिनके कोण B और M समकोण हैं।
सिद्ध करना है : (i) ∆ABC ~ ∆AMP में
(ii) \(\frac{\mathbf{C A}}{\mathbf{P A}}=\frac{\mathbf{B C}}{\mathbf{M P}}\)
उपपत्ति : ∆ABC और ∆AMP में,
∠A = ∠A (उभयनिष्ठ)
∠B = ∠M (प्रत्येक 90°)
∴ ∆ABC – ∆AMP (AA समरूपता)
∴ \(\frac{A C}{A P}=\frac{B C}{M P}\) [यदि दो त्रिभुज समरूप हों, तो संगत भुजाएँ समानुपाती होती हैं।

\(\frac{\mathrm{CA}}{\mathrm{PA}}=\frac{\mathrm{BC}}{\mathrm{MP}}\)

प्रश्न 10.
CD और GH क्रमश: ∠ACB और ∠EGF के ऐसे समद्विभाजक हैं कि बिंदु D और H क्रमशः ∆ABC और ∆FEG की भुजाओं AB और FE पर स्थित हैं। यदि ∆ABC ~ ∆FEG हैं, तो दर्शाइए कि :
(i) \(\)
(ii) ∆DCB ~ ∆HGE
(ii) ∆DCA ~ ∆HGF
हल:

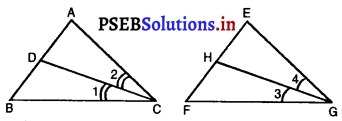
दिया है : ∆ABC और ∆FEG में, CD और GH
क्रमश: ∠ACB और ∠EGF के समद्विभाजक हैं अर्थात ∠1 = ∠2 और ∠3 = ∠4 है।
∆ABC – ∆FEG
सिद्ध करना है : (i) \(\)
(ii) ∆DCB ~ ∆HGE
(iii) ∆DCA ~ ∆HGE
उपपत्ति : (i) ∆ABC ~ ∆FEG (दिया है)
∠C = ∠G [यदि दो त्रिभुज समरूप हों, तो संगत कोण बराबर होते हैं।
\(\frac{1}{2}\) ∠C = \(\frac{1}{2}\) ∠G
∠1 = ∠3 या ∠2 = ∠4

अब, ∆ACD और ∆FGH में,
∠A = ∠F [प्रमाणित ऊपर]
∠2 = ∠4 [प्रमाणित ऊपर]
∴ ∆ACD ~ ∆FGH
[∵ AA प्रमाणित समरूपता कसौटी से] |
CD AG Also, GH FG
[∵ समरूप त्रिभुजों की संगत भुजाएँ समानुपाती होती हैं।

(ii) अब, ∆DCB और ∆HGE में,
∠B = ∠E [प्रमाणित ऊपर]
∠1 = ∠3 [प्रमाणित ऊपर]
∆DCB ~ ∆HGE
[∵ AA समरूपता कसौटी से]

(iii) अब, ∆DCA और ∆HGF में,
∠A = ∠F [प्रमाणित ऊपर)
∴ ∠2 = ∠4 [प्रमाणित ऊपर]
∆DCA ~ ∆HGF [∵ AA समरूपता कसौटी से]

प्रश्न 11.
आकृति में, AB = AC वाले, एक समद्विबाहु त्रिभुज ABC की बढ़ाई गई भुजा CB पर स्थित E एक बिंदु है। यदि AD ⊥ BC और EF ⊥ AC है, तो सिद्ध कीजिए कि ∆ABD ~ ∆ECF है।
हल :

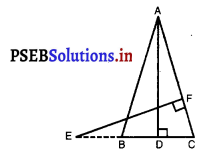
दिया है : AB = AC वाले एक समद्विबाहु ∆ABC की बढ़ाई गई भुजा CB पर स्थित E एक बिंदु है। AD ⊥ BC और EF ⊥ AC हैं।
सिद्ध करना है : ∆ABD ~ ∆ECF
उपपत्ति : ∆ABC समद्विबाहु त्रिभुज है (दिया है)
AB = AC (त्रिभुज में समान भुजाओं के सम्मुख कोण बराबर | होते है)
∴ ∠B = ∠C (बराबर कोण)
∆ABD और ∆ECF में,
∠ABD = ∠ECF (ऊपर प्रमाणित)
∠ADB = ∠EFC (प्रत्येक 90°)
∴ ∆ABD ~ ∆ECF [AA समरूपता]

प्रश्न 12.
एक त्रिभुज ABC की भुजाएँ AB और BC तथा माध्यिका AD एक अन्य त्रिभुज PQR की क्रमश : भुजाओंPQ औरQR तथा माध्यिका PM के समानुपाती हैं (देखिए आकृति) दर्शाइए कि ∆ABC ~ ∆PQR है।
हल :

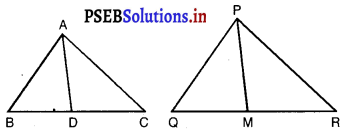
दिया है : ∆ABC और ∆PQR, ∆ABC की भुजाएँ AB, BC और माध्यिका AD एक अन्य त्रिभुज PQR की क्रमशः भुजाओं PQ और QR तथा माध्यिका PM के समानुपाती हैं
अर्थात् : \(\frac{\mathrm{AB}}{\mathrm{PQ}}=\frac{\mathrm{AC}}{\mathrm{PR}}=\frac{\mathrm{AD}}{\mathrm{PM}}\)
सिद्ध करना है : ∆ABC ~ ∆PQR

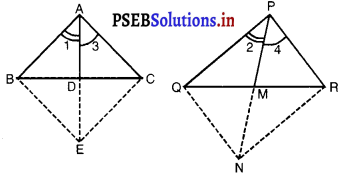
रचना : AD को E तक बढ़ाइए ताकि AD = DE और PM को N तक बढ़ाइए ताकि PM = MN हो।
BE, CE, QN और RN को मिलाइए।
उपपत्ति: \(\frac{\mathrm{AB}}{\mathrm{PQ}}=\frac{\mathrm{AC}}{\mathrm{PR}}=\frac{\mathrm{AD}}{\mathrm{PM}}\) (दिया है) …………….(1)
BD = DC (दिया है)
AD = DE
रचना: चतुर्भुज ABEC के विकर्ण परस्पर समद्विभाजित करता | है।
∴ चतुर्भुज ABEC एक समांतर चतुर्भुज है। इसी प्रकार, PONR एक समांतर चतुर्भुज है।
∴ BE = AC {समांतर चतुर्भुज की सम्मुख भुजाएँ) और QN = PR
\(\frac{\mathrm{BE}}{\mathrm{AC}}\) = 1 …………….(i)

\(\frac{\mathrm{QN}}{\mathrm{PR}}\) = 1 ……………..(ii)
(i) और (ii) से,

∴ ∆ABE ~ ∆PQN [भुजाएँ समानुपाती हैं]
∴ ∠1 = ∠2 ………..(4) [समरूप त्रिभुजों के संगत कोण] इसी प्रकार,
∆ACE ~ ∆PRN
∠3 = ∠4 ………..(5) [समरूप त्रिभुजों के संगत कोण]
(4) और (5) को जोड़ने पर,
∠1 + ∠3 = ∠2 + ∠4
∠A = ∠P
अब ∆ABC और ∆PQR में,
∠A = ∠P (प्रमाणित)
\(\frac{\mathrm{AB}}{\mathrm{PQ}}=\frac{\mathrm{AC}}{\mathrm{PR}}\) (दिया है)
∴ ∆ABC ~ ∆PQR
[ SAS समरूपता कसौटी के प्रयोग से]

प्रश्न 13.
एक त्रिभुज ABC की भुजा BC पर एक बिंदु D इस प्रकार स्थित है कि ∠ADC = ∠BAC है। दर्शाइए कि CA² = CB . CD है।
हल :
दिया है : ∆ABC की भुजा BC पर एक बिंदु D 57 Yar foretage foto ∠ADC = ∠BAC
सिद्ध करना है : CA² = BC × CD
उपपत्ति : ∆ABC और ∆ADC में,

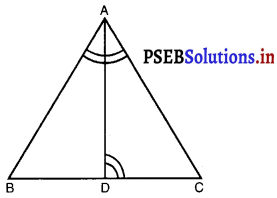
∠C = ∠C (उभयनिष्ठ)
∠BAC = ∠ADC (दिया है)
∴ ∆ABC ~ ∆DAC [AA समरूपता कसौटी से]
∴ \(\frac{\mathrm{AC}}{\mathrm{DC}}=\frac{\mathrm{BC}}{\mathrm{AC}}\) [दो त्रिभुजः समरूप हों ता संगत भुजाएँ समानुपाती होती हैं।]
AC² = BC . DC

प्रश्न 14.
एक त्रिभुज ABC की भुजाएँ AB और AC तथा माध्यिका AD एक अन्य त्रिभुज की भुजाओं PQ और PR तथा माध्यिका PM के क्रमशः समानुपाती हैं। दर्शाइए कि ∆ABC ~ ∆PQR है।
हल :
दिया है : दो त्रिभुज ABC और PQR में D, BC का मध्य-बिंदु है और M, QR का मध्य-बिंदु है।

और \(\frac{\mathrm{AB}}{\mathrm{PQ}}=\frac{\mathrm{AC}}{\mathrm{PR}}=\frac{\mathrm{AD}}{\mathrm{PM}}\) ………………(1)

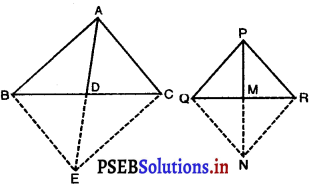
सिद्ध करना है : ∆ABC ~ ∆PQR
रचना : AD को E तक बढ़ाइए ताकि AD = DE हों।
BE और CE को मिलाइए।
PM को N तक बढ़ाइए ताकि PM = MN हो।
QN और NR को मिलाइए।
उपपत्ति : चतुर्भुज ABEC के विकर्ण AE और BC परस्पर D पर समद्विभाजित करते हैं।
∴ चतुर्भुज ABEC एक समांतर चतुर्भुज है।
इसी प्रकार यह दर्शाया जा सकता है कि चतुर्भुज PQNR एक समांतर चतुर्भुज है।
चूँकि ABEC एक समांतर चतुर्भुज है।
∴ BE = AC …………..(2)
इसी प्रकार चूँकि PQNR एक || gm है।
∴ QN = PR …………….(3)
(2) को (3) से विभाजित करने पर हमें प्राप्त होता है

इसी प्रकार, यह सिद्ध किया जाता है कि
∆AEC ~ ∆PNR
∴ ∠EAC = ∠NPR ……….(7)
(6) और (7) को जोड़ने पर हमें प्राप्त होता है।
∠BAE + ∠EAC = ∠QPN + ∠NPR
अर्थात् ∠BAC = ∠QPR
अब ∆ABC और ∆PQR में
\(\frac{\mathrm{AB}}{\mathrm{PQ}}=\frac{\mathrm{AC}}{\mathrm{PR}}\)
∠A = ∠P
∴ ∆ABC ~ ∆QPR (SAS समरूपता कसौटी से)

प्रश्न 15.
लंबाई 6 m वाले एक उर्ध्वाधर स्तंभ की भूमि पर छाया की लंबाई 4 m है, जबकि उसी समय एक मीनार की छाया की लंबाई 28 m है।मीनार की ऊँचाई ज्ञात कीजिए।
हल:

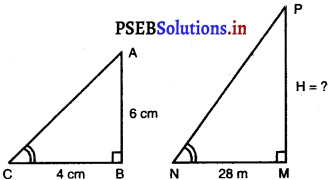
उर्ध्वाधर स्तंभ की लंबाई = 6 m
स्तंभ की छाया की लंबाई = 4 m
मान लीजिए मीनार की ऊँचाई = Hm
मीनार की छाया की लंबाई = 28 m
∆ABC और ∆PMN में,
∠C = ∠N (मीनार की छाया की लंबाई)
∠B = ∠M (प्रत्येक 90°)
∴ ∆ABC ~ ∆PMN [AA समरूपता कसौटी]
∴ \(\frac{\mathrm{AB}}{\mathrm{PM}}=\frac{\mathrm{BC}}{\mathrm{MN}}\) [यदि दो त्रिभुजें समरूप हों, तो उनकी संगत भुजाएँ समानुपाती होती हैं।

∴ \(\frac{6}{H}=\frac{4}{28}\)
H = 6 × 7
H = 42 m
∴ मीनार की ऊँचाई = 42 m.

प्रश्न 16.
AD और PM त्रिभुजों ABC और PQR की क्रमशः माध्यिकाएँ हैं, जबकि ∆ABC ~ ∆PQR है। सिद्ध कीजिए कि P-Bहै।

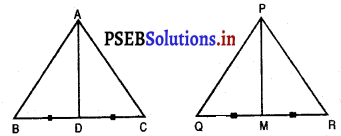
हल : दिया है : ∆ABC और ∆PQR की AD और PM माध्यिकाएँ हैं तथा ∆ABC ~ ∆PQR है।
सिद्ध करना है : \(\frac{\mathrm{AB}}{\mathrm{PQ}}=\frac{\mathrm{AD}}{\mathrm{PM}}\)
उपपत्ति : ∆ABC ~ ∆PQR (दिया है)
∴ \(\frac{\mathrm{AB}}{\mathrm{PQ}}=\frac{\mathrm{BC}}{\mathrm{QR}}=\frac{\mathrm{AC}}{\mathrm{PR}}\) {यदि दो त्रिभुजें समरूप हैं तो उनकी संगत भुजाएँ समानुपाती होती हैं।
∠A = ∠P {यदि दो त्रिभुजें समरूप हैं, तो उनके संगत कोण बराबर होते हैं।}
∠B = ∠Q
∠C = ∠R
D, BC का मध्य-बिंदु है।
∴ BD = DC = \(\frac{1}{2}\) BC
M, OR का मध्य-बिंदु है।
∴ QM = MR = \(\frac{1}{2}\) OR

\(\frac{\mathrm{AB}}{\mathrm{PQ}}=\frac{\mathrm{BC}}{\mathrm{QR}}\) ………………..(3)

\(\frac{\mathrm{AB}}{\mathrm{PQ}}=\frac{2 \mathrm{BD}}{2 \mathrm{QM}}\) ((2) और (3) से)

\(\frac{\mathrm{AB}}{\mathrm{PQ}}=\frac{\mathrm{BD}}{\mathrm{QM}}\)

∠ABD = ∠PQM
(दिया है) ∆ABC ~ ∆PQM (SAS समरूपता कसौटी से)
\(\frac{\mathrm{AB}}{\mathrm{PQ}}=\frac{\mathrm{AD}}{\mathrm{PM}}\) [यदि दो त्रिभुजें समरूप हैं तो उनकी संगत भुजाएँ समानुपाती होती हैं।