PSEB 10th Class Maths Solutions Chapter 6 त्रिभुज Ex 6.4

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 6 त्रिभुज Ex 6.4 Textbook Exercise Questions and Answers

PSEB Solutions for Class 10 Maths Chapter 6 त्रिभुज Ex 6.4

प्रश्न 1. मान लीजिए ∆ABC ~ ∆DEF है और इनके क्षेत्रफल क्रमशः 64 cm² और 121 cm2 हैं। यदि EF = 15.4 cm हो, तो BC ज्ञात कीजिए। हल : ∆ABC ~ ∆DEF, AABC का क्षेत्रफल = 64 cm² और ∆DEF का क्षेत्रफल = 121 cm² और EF = 15.4 cm है। . 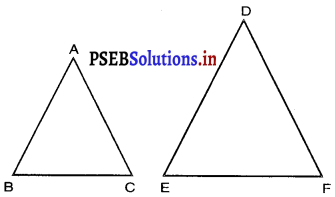∆ABC ~ ∆DEF ∴ \(\frac{\ {ar}(\triangle \mathrm{ABC})}{\ {ar}(\triangle \mathrm{DEF})}=\frac{\mathrm{AB}^{2}}{\mathrm{DE}^{2}}=\frac{\mathrm{AC}^{2}}{\mathrm{DF}^{2}}=\frac{\mathrm{BC}^{2}}{\mathrm{EF}^{2}}\) (यदि दो त्रिभुजें समरूप हों तो उनके क्षेत्रफलों का अनुपात संगत भुजाओं के अनुपात के वर्ग के बराबर होता है।) \(\frac{64}{121}=\frac{\mathrm{BC}^{2}}{\mathrm{EF}^{2}}\) \(\left(\frac{8}{11}\right)^{2}=\left(\frac{B C}{15.4}\right)^{2}\) \(\frac{8}{11}=\frac{B C}{15.4}\) BC = \(\frac{8 \times 15.4}{11}\) BC = 8 × 1.4 BC = 11.2 cm. प्रश्न 2. एक समलंब ABCD जिसमें AB || DC है, के विकर्ण परस्पर बिंदु 0 पर प्रतिच्छेद करते हैं। यदि AB = 2 CD हो, तो त्रिभुजों AOB और COD के क्षेत्रफलों का अनुपात ज्ञात कीजिए। हल : ABCD एक समलंब है जिसमें AB || DC है, के विकर्ण AC और BD परस्पर बिंदु 0 पर प्रतिच्छेद करते हैं। AB = 2 CD है। 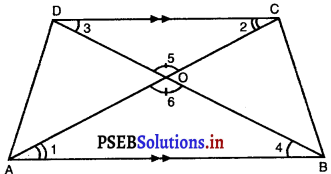∆AOB और ∆COD में, ∠1 = ∠2 (एकांतर कोण) ∠3 = ∠4 (एकांतर कोण) ∠5 = ∠6 (शीर्षाभिमुख कोण)। ∴ ∆AOB ~ ∆COD \(\frac{\ {ar}(\triangle \mathrm{AOB})}{\ {ar}(\Delta \mathrm{COD})}=\frac{\mathrm{AB}^{2}}{\mathrm{CD}^{2}}\) {यदि दो त्रिभुजें समरूप हों, तो उनके क्षेत्रफलों का अनुपात उनकी संगत भुजाओं के अनुपात का वर्ग होता है।} = \(\frac{(2 \mathrm{CD})^{2}}{\mathrm{CD}^{2}}\) \(\frac{\ {ar}(\triangle \mathrm{AOB})}{\ {ar}(\triangle \mathrm{COD})}=\frac{4 \mathrm{CD}^{2}}{\mathrm{CD}^{2}}=\frac{4}{1}\) ∴ वांछित ar ∆AOB और ar ∆COD का अनुपात = 4 : 1 प्रश्न 3. आकृति में एक ही आधार BC पर दो त्रिभुज ABC और DBC बने हुए हैं। यदि AD, BC को 0 पर प्रतिच्छेद करे, तो दर्शाइए कि \(\frac{\ {ar}(\triangle \mathrm{AOB})}{\ {ar}(\Delta \mathrm{COD})}=\frac{\mathrm{AO}}{\mathrm{DO}}\) है| 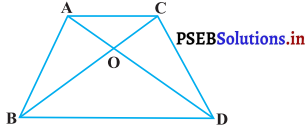हल: दिया है : AABC और ADBC एक ही आधार BC पर बने हुए हैं। AD, BC को 0 पर प्रतिच्छेद करती है। 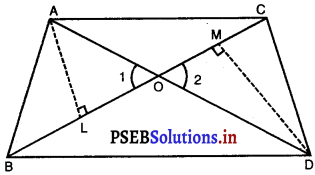सिद्ध कीजिए : \(\frac{\ {ar}(\triangle \mathrm{ABC})}{\ {ar}(\triangle \mathrm{DBC})}=\frac{\mathrm{AO}}{\mathrm{DO}}\) रचना : AL ⊥ BC, DM ⊥ BC खींचिरा उपपत्ति : ∆ALO और ∆DMO में, ∠1 = ∠2 (शीर्षाभिमुख कोण) ∠L = ∠M (प्रत्येक 90°) ∴ ∆ALO ~ ∆DMO [AA समरूपता कसौटी] ∴ \(\frac{\mathrm{AL}}{\mathrm{DM}}=\frac{\mathrm{AO}}{\mathrm{DO}}\) …………….(1) [यदि दो त्रिभुजें समरूप हों, तो संगत भुजाएँ समानुपाती होती हैं।]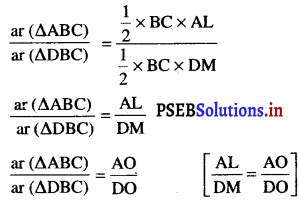 प्रश्न 4. यदि दो समरूप त्रिभुजों के क्षेत्रफल बराबर हों तो सिद्ध कीजिए कि वे त्रिभुज सर्वांगसम होते हैं। हल : दिया है : दो त्रिभुजें ABC और DEF समरूप हैं और क्षेत्रफल में बराबर हैं। सिद्ध करना है : ∆ABC ≅ ∆DEF 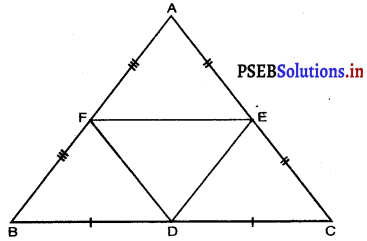उपपत्ति : चूँकि ∆ABC ~ ∆DEF, ∴ \(\frac{\ {ar}(\triangle \mathrm{ABC})}{\ {ar}(\triangle \mathrm{DEF})}=\frac{\mathrm{BC}^{2}}{\mathrm{EF}^{2}}\) \(\frac{\mathrm{BC}^{2}}{\mathrm{EF}^{2}}\) = 1 ⇒ BC² = EF² ⇒ BC = EF. साथ ही, चूँकि ∆ABC ~ ∆DEF, इसलिए वे समकोणिक हैं और ∠B = ∠E और ∠C =∠F. अब त्रिभुजों ABC और DEF में, ∠B = ∠E, ∠C = ∠F और BC = EF ∴ ∆ABC = ∆DEF (ASA सर्वांगसमता प्रमेय) प्रश्न 5. एक त्रिभुज ABC की भुजाओं AB, BC और CA के मध्य-बिंदु क्रमशः D, E और F हैं। ∆DEF और ∆ABC के क्षेत्रफलों का अनुपात ज्ञात कीजिए। हल: दिया है : एक ∆ABC की भुजाओं AB, BC और CA के मध्य-बिंदु क्रमश: D, E और F हैं। अभीष्ट : ar (∆DEF) : ar (∆ABC) ज्ञात करना। उपपत्ति : ∆ABC में, F, AB का मध्य-बिंदु है। …(दिया है) E, AC का मध्य-बिंदु है। …(दिया है) इसलिए मध्य-बिंदु प्रमेय से, FE || BC और FE = \(\frac{1}{2}\) BC ⇒ FE || BD . और FE = BD [∵ BD = \(\frac{1}{2}\) BC] ∴ BDEF एक समांतर चतुर्भुज है (∵ सम्मुख भुजाएँ समांतर और समान हैं।) त्रिभुजों FBD और DEF में, FB = DE …(|| gm BDEF की सम्मुख भुजाएँ) FD = FD …(उभयनिष्ठ) ….|(| gm BDEF की सम्मुख भुजाएँ) BD = FE ∴ ∆FBD = ∆DEF ….. (SSS सर्वांगसमता प्रयोग) इसी प्रकार, हम सिद्ध कर सकते हैं कि ∆AFE = ∆DEF और ∆EDC = ∆DEF यदि त्रिभुजें सर्वांगसम हों, तो वे क्षेत्रफल में बराबर होती हैं। ∴ ar (∆FBD) = ar (∆DEF) …………(1) ar (∆AFE) = ar (∆DEF) ………..(2) ar (∆EDC) = ar (∆DEF) ……………..(3) अब ar ∆(ABC) = ar (∆FBD) + ar (∆DEF) + ar (∆AFE) + ar (AEDC) = ar (ADEF) + ar (ADEF) + ar (ADEF) + ar (ADEF) [(1), (2) और (3) का प्रयोग करने पर] = 4 ar (∆DEF) = ar (∆DEF) = \(\frac{1}{4}\) ar (∆ABC) ⇒ \(\frac{\ {ar}(\triangle \mathrm{DEF})}{\ {ar}(\triangle \mathrm{ABC})}=\frac{1}{4}\) ∴ ar (∆DEF) : ar (∆ABC) = 1 : 4. प्रश्न 6. सिद्ध कीजिए कि दो समरूप त्रिभुजों के क्षेत्रफलों का अनुपात इनकी संगत माध्यिकाओं के अनुपात का वर्ग होता है। दिया है : ∆ABC ~ ∆DEF. AX और DY क्रमशः भुजाओं BC और EF की माध्यिकाएँ हैं। 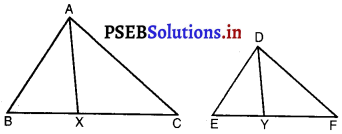प्रश्न 7. सिद्ध कीजिए कि एक वर्ग की किसी भुजा पर बनाए गए समबाहु त्रिभुज का क्षेत्रफल उसी वर्ग के एक विकर्ण पर बनाए गए समबाहु त्रिभुज के क्षेत्रफल का आधा होता है। हल : दिया है : ABCD एक वर्ग है। समबाहु ∆ABC वर्ग की भुजा AB पर स्थित है और समबाहु ∆ACF विकर्ण AC पर बनी हैं। 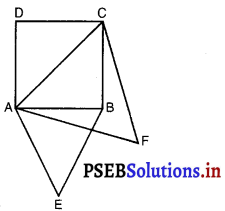सिद्ध कीजिए : \(\frac{\ {ar}(\triangle \mathrm{ABC})}{\ {ar}(\triangle \mathrm{ACF})}=\frac{1}{2}\) उपपत्ति : समकोण ∆ABC में, AB² + BC² = AC² [पाइथागोरस प्रमेय द्वारा] = AB² + AB² = AC² [∵ AB = BC, एक ही वर्ग की भुजाएँ] ∴ 2AB² = AC² ………………(1) अब, प्रत्येक ∆ABE और ∆ACF समबाहु और इसलिए समकोणिक हैं और इसलिए समरूप हैं। अर्थात् ∆ABE ~ ∆ACF. यहाँ पहली ∆ की कोई भुजा दूसरी त्रिभुज की किसी भुजा से समांतर हैं। ∴ \(\frac{\ {ar}(\triangle \mathrm{ABE})}{\ {ar}(\triangle \mathrm{ACF})}=\frac{\mathrm{AB}^{2}}{\mathrm{AC}^{2}}\) [:: दो समरूप त्रिभुजों के क्षेत्रफलों का अनुपात उनकी संगत भुजाओं के अनुपात के वर्ग के बराबर होता है।] = \(\frac{\mathrm{AB}^{2}}{2 \mathrm{AB}^{2}}=\frac{1}{2}\). [(1) का प्रयोग करने पर] सही उत्तर चुनिए और अपने उत्तर का औचित्य दीजिए: प्रश्न 8. ABC और BDE दो समबाहु त्रिभुज इस प्रकार हैं कि D भुजा BC का मध्य-बिंदु है। त्रिभुजों ABC और BDE के क्षेत्रफलों का अनुपात है : (A) 2 : 1 (B) 1 : 2 (C) 4 : 1 (D) 1 : 4. हल :- ∆ABC और ∆BDE दो समबाहु त्रिभुज इस प्रकार है कि D भुजा BC का मध्य-बिन्दु है। ∴ BD = DC = \(\frac{1}{2}\) BC, मान लीजिए समबाहु त्रिभुज की भुजा 2a है। ∴ ∆ABC ~ ∆BDE ∴ \(\frac{\ {ar}(\triangle \mathrm{ABC})}{\ {ar}(\triangle \mathrm{BDE})}=\frac{\mathrm{AB}^{2}}{\mathrm{BD}^{2}}\) = \(\frac{(2 a)^{2}}{(a)^{2}}=\frac{4 a^{2}}{a^{2}}\) = \(\frac{4}{1}\) ∴ (C) सही विकल्प है प्रश्न 9. दो समरूप त्रिभुजों की भुजाएँ 4:9 के अनुपात में हैं। इन त्रिभुजों के क्षेत्रफलों का अनुपात है : (A) 2 : 3 (B) 4 : 9 (C) 81 : 16 (D) 16 : 81. हल: 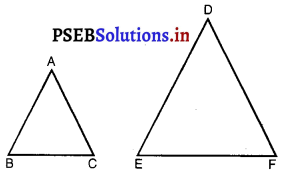(दिया है) ∆ABC ~ ∆DEF \(\frac{\mathrm{AB}}{\mathrm{DE}}=\frac{\mathrm{AC}}{\mathrm{DF}}=\frac{\mathrm{BC}}{\mathrm{EF}}=\frac{4}{9}\) ∴ \(\frac{\ {ar}(\Delta \mathrm{ABC})}{\ {ar}(\Delta \mathrm{DEF})}=\frac{\mathrm{AB}^{2}}{\mathrm{DE}^{2}}\) [दो समरूप त्रिभुजों के क्षेत्रफलों का अनुपात उनकी संगत भुजाओं के अनुपात के वर्ग के बराबर होता है] ∴ \(\frac{\ {ar}(\triangle \mathrm{ABC})}{\ {ar}(\Delta \mathrm{DEF})}=\left(\frac{4}{9}\right)^{2}=\frac{16}{81}\) ∴ (D) सही विकल्प है।