PSEB 10th Class Maths Solutions Chapter 6 त्रिभुज Ex 6.5

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 6 त्रिभुज Ex 6.5 Textbook Exercise Questions and Answers

PSEB Solutions for Class 10 Maths Chapter 6 त्रिभुज Ex 6.5

प्रश्न 1.
कुछ त्रिभुजों की भुजाएँ नीचे दी गई हैं। निर्धारित कीजिए कि इनमें से कौन-कौन से त्रिभुज समकोण त्रिभुज हैं। इस स्थिति में कर्ण की लंबाई भी लिखिए।
(i) 7 cm, 24 cm, 25 cm
(ii) 3 cm, 8 cm, 6 cm
(iii) 50 cm, 80 cm, 100 cm
(iv) 13 cm, 12 cm, 5 cm.
हल :
(i) मान लीजिए ∆ABC में,
AB = 7 cm, BC = 24 cm, AC = 25 cm
AB² + BC² = (7)² + (24)²
= 49 + 576 = 625
AC² = (25)² = 625
अब AB² + BC² = AC²
∴ ∆ ABC एक समकोण त्रिभुज है।

(ii) मान लीजिए APQR में,
PQ = 3 cm, QR = 8 cm, PR = 6 cm
PQ² + PR² = (3)² + (6)²
= 9 + 36 = 45
QR² = (8)² = 64.
यहाँ PQ² + PR² ≠ QR²
∴ ∆ PQR समकोण त्रिभुज नहीं है।

(iii) मान लीजिए ∆MNP में, MN = 50 cm, NP = 80 cm, MP = 100 cm
MN² + NP² = (50)² + (80)²
= 2500 + 6400 = 8900
MP² = (100)² = 10000
यहां MP² + MN² + NP².
∴ ∆MNP समकोण त्रिभुज नहीं है।

(iv) मान लीजिए ∆ABC में,
AB = 13 cm, BC = 12 cm,
AC = 5 cm BC² + AC²
= (12)² + (5)²
= 144 + 25 = 169
AB² = (13)² = 169
∴ AB² = BC² + AC²
∆ABC समकोण त्रिभुज है।

प्रश्न 2.
POR का समकोण त्रिभज है जिसका कोण P समकोण है तथा QR पर बिंदु M इस प्रकार स्थित है कि PM ⊥ QR है। दर्शाइए कि PM² = QM.MR है।
हल:
दिया है : समकोण ∆PQR में कोण P समकोण है।Q पर बिंदु M इस प्रकार स्थित है कि PM ⊥ QR है।
सिद्ध करना है : PM² = QM × MR

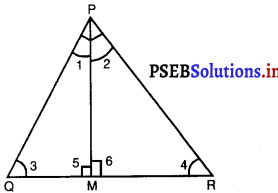
(दिया है)

उपपत्ति:
∠P = 90°
∠1 + ∠2 = 90° ………………(1)
∠M = 90°
∆PMQ में,
∠1 + ∠3 + ∠n = 180°
∠1 + ∠3 = 90° ……………..(2)
[∠M = 90°]
(1) और (2) से,
∠1 + ∠2 = ∠1 + ∠3
∠2 = ∠3
∆QPM और ∆RPM में,
∠3 = ∠2 (प्रमाणित)
∠5 = ∠6 (प्रत्येक 90°)
∴ ∆QMP ~ ∆PMR [AA समरूपता]

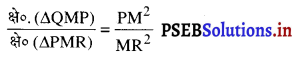
[यदि दो त्रिभुजें समरूप हैं, तो उनके क्षेत्रफलों का अनुपात उनकी संगत भुजाओं के वर्गों के अनुपात के बराबर होता है।]

\(\frac{\frac{1}{2} \mathrm{QM} \times \mathrm{PM}}{\frac{1}{2} \mathrm{RM} \times \mathrm{PM}}=\frac{\mathrm{PM}^{2}}{\mathrm{MR}^{2}}\)

[∵ A का क्षेत्रफल = \(\frac{1}{2}\) × आधार × शीर्षलम्ब]

\(\frac{\mathrm{QM}}{\mathrm{RM}}=\frac{\mathrm{PM}^{2}}{\mathrm{RM}^{2}}\)

PM² = QM × RM

प्रश्न 3.
आकृति में, ABD एक समकोण त्रिभुज है जिसका कोणA समकोण है तथा AC ⊥ BD है।दर्शाइए कि
(i) AB² = BC.BD
(ii) AC² = BC.DC
(iii) AD = BC.CD.

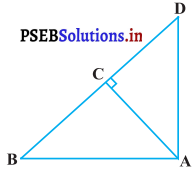
हल :
∆DAB और ∆DCA में,
∠D = ∠D (उभयनिष्ठ)
∠A = ∠C (प्रत्येक 90°)
∴ ∆DAB ~ ∆DCA [AA समरूपता]
∆DAB और ∆ACB में, ……………….(1)
∠B = ∠B (उभयनिष्ठ)
∠A = ∠C (प्रत्येक 90°)
∴ ∆DAB ~ ∆ACB ……………..(2)
(1) और (2) से,
∆DAB ~ ∆ACB ~ ∆DCA.
(i) ∆ACB~ ∆DAB (प्रमाणित)

∴ \(\frac{(\Delta \mathrm{ACB})}{(\Delta \mathrm{DAB})}=\frac{\mathrm{AB}^{2}}{\mathrm{DB}^{2}}\)

[यदि दो त्रिभुजें समरूप हैं, तो उनके क्षेत्रफलों का अनुपात उनकी संगत भुजाओं के वर्गों के अनुपात के बराबर होता है।]

\(\frac{\frac{1}{2} \mathrm{BC} \times \mathrm{AC}}{\frac{1}{2} \mathrm{DB} \times \mathrm{AC}}=\frac{\mathrm{AB}^{2}}{\mathrm{DB}^{2}}\)

[∵ त्रिभुज का क्षेत्रफल = \(\frac{1}{2}\) आधार × शीर्षलम्ब]

BC = \(\frac{\mathrm{AB}^{2}}{\mathrm{BD}}\)
AB² = BC × BD.

(ii) ∆ACB ~ ∆DCA (प्रमाणित)

\(\frac{(\Delta \mathrm{ACB})}{(\Delta \mathrm{DCA})}=\frac{\mathrm{AC}^{2}}{\mathrm{DC}}\)

[यदि दो त्रिभुजें समरूप हों, तो उनके क्षेत्रफलों का अनुपात संगत भुजाओं के अनुपात के वर्ग के बराबर होता है।]

\(\frac{\frac{1}{2} \mathrm{BC} \times \mathrm{AC}}{\frac{1}{2} \mathrm{DC} \times \mathrm{AC}}=\frac{\mathrm{AC}^{2}}{\mathrm{DC}^{2}}\)

[∵ त्रिभुज का क्षेत्रफल = \(\frac{1}{2}\) आधार × शीर्षलम्ब]

BC = \(\frac{\mathrm{AC}^{2}}{\mathrm{DC}}\)

AC² = BC × DC

(iii) ∆DAB ~ ∆DCA (प्रमाणित)

\(\frac{(\triangle \mathrm{DAB})}{(\Delta \mathrm{DCA})}=\frac{\mathrm{DA}^{2}}{\mathrm{DB}^{2}}\)

[यदि दो त्रिभुजें समरूप हों, तो उनके क्षेत्रफलों का अनुपात संगत भुजाओं के अनुपात के वर्ग के बराबर होता है।

\(\frac{\frac{1}{2} \mathrm{CD} \times \mathrm{AC}}{\frac{1}{2} \mathrm{BD} \times \mathrm{AC}}=\frac{\mathrm{AD}^{2}}{\mathrm{BD}^{2}}\)

CD = \(\frac{\mathrm{AD}^{2}}{\mathrm{BD}}\)

→ AD² = BD × CD.

प्रश्न 4.
ABC एक समद्विबाहु त्रिभुज है जिसका कोण C समकोण है। सिद्ध कीजिए कि AB² = 2AC है।
हल :
दिया है : ∆ABC एक समद्विबाहु त्रिभुज है जिसका कोण C समकोण है।
सिद्ध करना है : AB² = 2AC².
उपपत्ति : ∆ACB में, ∠C = 90°
AC = BC (दिया है)
AB² = AC² + BC²
[पाइथागोरस प्रमेय से]
= AC² + AC² [BC = AC]
AB² = 2 AC²

प्रश्न 5.
ABC एक समद्विबाहु त्रिभुज है जिसमें AC = BC है। यदि AB² = 2AC² है, तो सिद्ध कीजिए कि ABC एक समकोण त्रिभुज है।
हल :
दिया है. : ∆ABC एक समद्विबाहु त्रिभुज है जिसका कोण AC = BC है।
AB² = 2AC².
सिद्ध करना है : ∆ABC एक समकोण त्रिभुज है।

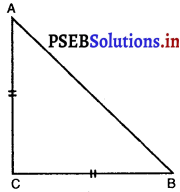
उपपत्ति: AB² = 2AC²
(दिया है) AB² = AC² + A²
AB² = AC² + BC² [AC = BC]
∴ पाइथागोरस प्रमेय के विलोम से, ∆ABC समकोण त्रिभुज है।

प्रश्न 6.
एक समबाहु त्रिभुज ABC की भुजा 2a है। उसके प्रत्येक शीर्षलंब की लंबाई ज्ञात कीजिए।
हल :
∆ABC समबाहु त्रिभुज है जिसकी भुजा 2a है।
AD ⊥ BC
AB = AC = BC = 2a
∆ADB = ∆ADC [RHS सर्वांगसमता से]
∴ BD = DC = a

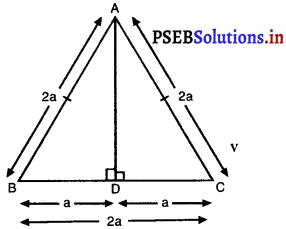
समकोण ∆ADB में,
AB² = AD² + BD²
(2a)² = AD² + (a)²
4a² – a² = AD².
AD² = 3a²
∴ AD = √3a.

प्रश्न 7.
सिद्ध कीजिए कि एक समचतुर्भुज की भुजाओं के वर्गों का योग उसके विकर्णों के वर्गों के योग के बराबर होता है।
हल :
दिया है : समचतुर्भज ABCD के विकर्ण AC और BD परस्पर 0 पर प्रतिच्छेद करते हैं।
सिद्ध करना है : AB² + BC² + CD² + AD² = AC² + BD²
उपपत्ति: समचतुर्भुज के विकर्ण परस्पर समकोण पर समद्विभाजित होते हैं। ………………(1)

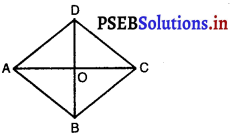
∴ AO = CO, BO = DO
∴ O पर कोण समकोण हैं
∆AOB में, ∠AOB = 90°
∴ AB² = AO² + BO²
[पाइथागोरस प्रमेय से]
इसी प्रकार, BC² = CO² + BO² ……………(2)
CD² = CO² + DO² ………….(3)
और DA² = DO² + AO² ……………(4)
(1), (2), (3) और (4) को जोड़ने पर हमें प्राप्त होता है।
AB² + BC² + CD² + DA² = 2AO² + 2CO² + 2BO² + 2DO²
= 4AO² + 4BO²
[∵ AO = CO और BO = DO]
= (2AO)² + (2BO)²
= AC² + BD².

प्रश्न 8.
आकृति में, ∆ABC के अभ्यंतर में स्थित कोई बिंदु O है तथा OD ⊥ BC, OE ⊥ AC और OF ⊥ AB है। दर्शाइए कि
(i) OA² + OB² + OC² – OD² – OE² – OF² = AF² + BD² + CE²
(ii) AF² + BD² + CE² = AE² + CD² + BF².

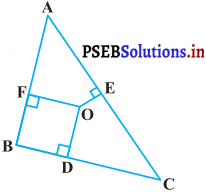
हल :
दिया है : एक ∆ABC जिसमें OD ⊥ BC, OE ⊥ AC और OF ⊥ AB है।
सिद्ध करना है: (i) AF² + BD² + CE² = OA² + OB² + OC² – OD² – OE² – OF²
(ii) AF² + BD² + CE² = AE² + CD² + BF²
उपपत्ति : (i) समकोण AAFO में,
OA² = OF² + AF² [पाइथागोरस प्रमेय से।]
या AF² = OA² – OF² …………….(1)
समकोण ∆BDO में,
OB² = BD² + OD² [पाइथागोरस प्रमेय से]
⇒ BD² = OB² – OD² ……………….(2)
समकोण ∆CEO में,
OC² = CE² + OE²
[पाइथागोरस प्रमेय से]
⇒ CE² = OC² – OE² ……………(3)
∴ AF² + CD² + CE² = OA² – OF² + OB² – OD² + OC² – OE²
[(1), (2), और (3) को जोड़ने पर]
= OA² + OB² + OC² – OD² – OE² – OF²
जोकि (1) को सिद्ध करता है।
पुन : AF² + BD² + CE²
= (OA² – OE²) + (OC² – OD²) + (OB² – OF²)
= AE² + CD² + BF²
[∵ AE² = AO² – OE²
CD² = OC² – OD²
BF² = OB² – OF²]

प्रश्न 9.
10 m लंबी एक सीढ़ी एक दीवार पर टिकाने पर भूमि से 8 m की ऊँचाई पर स्थित एक खिड़की तक पहुँचती है। दीवार के आधार से सीढ़ी के निचले सिरे की दूरी ज्ञात कीजिए।

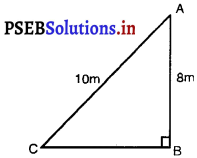
हल :
खिड़की की धरती से ऊँचाई (AB) = 8 m
10m
8m
सीढ़ी की लंबाई (AC) = 10 m
सीढ़ी के निचले सिरे और दीवार के आधार के बीच की दूरी (BC) = ?
∆ ABC में,
AB² + BC² = AC² [पाइथागोरस प्रमेय से।
(8)² + (BC)² = (10)²
64 + BC² = 100
BC² = 100 – 64
BC = √36
BC = 6 cm.
∴ सीढ़ी के निचले सिरे और दीवार के आधार के बीच की दूरी = 6 cm.

प्रश्न 10.
18 m ऊँचे एक ऊर्ध्वाधर खंभे के ऊपरी सिरे से एक तार का एक सिरा जुड़ा हुआ है तथा तार का दूसरा सिरा एक खूटे से जुड़ा हुआ है। खंभे के आधार से खूटे को कितनी दूरी पर गाड़ा जाए कि तार तना रहे जबकि तार की लंबाई 24 m है।
हल :
मान लीजिए खंभे की ऊँचाई AB = 18 m
तार की लंबाई, AC = 24 m

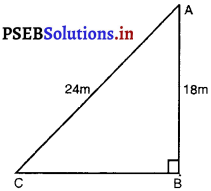
C, खूटे की स्थिति है। इसकी खंभे के आधार से दूरी BC = है।
समकोण ABC,
AB² + BC² = AC² [पाइथागोरस प्रमेय से।]
(18)² + (BC)² = (24)²
324 + (BC)² = 576
BC² = 576 – 324
BC = √252
BC = 6√7 m

प्रश्न 11.
एक हवाई जहाज़ एक हवाई अड्डे से उत्तर की ओर 1000 km/hr की चाल से उड़ता है। इसी समय एक अन्य हवाई जहाज़ उसी हवाई अड्डे से पश्चिम की
ओर 1200 km/hr की चाल से उड़ता है। 1\(\frac{1}{2}\) बाद दोनों हवाई जहाजों के बीच की दूरी कितनी होगी ?
हल :
पहले हवाई जहाज़ की चाल = 1000 km/hr.

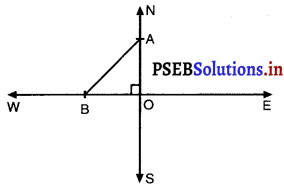
पहले हवाई जहाज़ द्वारा उत्तर की ओर 1 \(\frac{1}{2}\) घंटे में तय की गई दूरी = 1000 × \(\frac{3}{2}\) km = 1500 km
OA = 1500 km
दूसरे हवाई जहाज़ की चाल = 1200 km/hr.
दूसरे हवाई जहाज़ द्वारा 1 \(\frac{1}{2}\) घंटे में तय की गई दूरी = 1200 × \(\frac{3}{2}\)
OB = 1800 km.
समकोण ∆AOB में,
AB² = AO² + OB²
AB² = (1500)² + (1800)²
AB = \(\sqrt{2250000+3240000}\)
= \(\sqrt{5490000}\)
AB = 300 √61 km.
∴ दोनों हवाई जहाज़ों के बीच की दूरी = 300 √61 km

प्रश्न 12.
दो खंभे जिनकी ऊँचाईयाँ 6 m और 11 m हैं तथा ये समतल भूमि पर खड़े हैं। यदि इनके ऊपरी सिरों के बीच की दूरी 12 m है तो इनके ऊपरी सिरों के बीच की दूरी ज्ञात कीजिए।
हल :
खंभे की ऊँचाई, AB = 11m
खंभे की ऊँचाई (CD) = 6 m

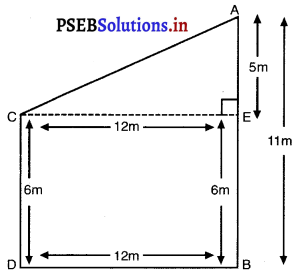
खंभों के आधारों में दूरी = 12 m
C से CE ⊥ AB खींचिए
BE = DC = 6m
AE = AB – BE
= (11 – 6) m = 5 m.
समकोण ∆AEC में, AC² = AE² + EC²
AC = \(\sqrt{(5)^{2}+(12)^{2}}\)
= \(\sqrt{25+144}\)
= √169 = 13.
∴ खंभों के ऊपरी सिरों के बीच की दूरी = 13m.

प्रश्न 13.
एक त्रिभुज ABC जिसका कोण C समकोण है, की भुजाओं CA और CB पर क्रमशः बिंदु D और E स्थित हैं। सिद्ध कीजिए कि AE² + BD² = AB² + DE² है।
हल :
दिया है :
∆ABC एक समकोण त्रिभुज है जिसमें C पर समकोण है भुजाओं CA और CB पर क्रमशः बिंदुD और E स्थित हैं।
अर्थात् CD = AD = \(\frac{1}{2}\) AC
BE = EC = \(\frac{1}{2}\) BC
सिद्ध करना है:
AE² + BD² = AB² + DE²
उपपत्ति : समकोण ABCA में,
AB² = BC² + CA² ………………(1)
[पाइथागोरस प्रमेय से]

समकोण AECD में,
DE² = EC² + DC² …………….(2)
पाइथागोरस प्रमेय से] समकोण ∆ACE में,
AE² = AC² + CE² ……………..(3)
समकोण ABCD में, BD² = BC² + CD² ……………..(4)
(3) और (4) को जोड़ने पर,
AE² + BD² = AC² + CE² + BC² + CD²
= [AC² + CB²] + [CE² + DC²]
= AB² + DE²
[(3) और (4) से]
अतः, AE² + BD² = AB² + DE².

प्रश्न 14.
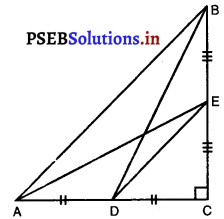
किसी त्रिभुज ABC के शीर्ष A से BC पर डाला गया लम्ब BC को बिंदु पर इस प्रकार प्रतिच्छेद करता है कि DB = 3 CD है ( देखिए आकृति)
सिद्ध कीजिए कि 2 AB² = 2 AC² + BC² है।
हल :
दिया है : ∆ABC में, AD ⊥ BC
BD = 3CD है।
सिद्ध करना है: 2AB² = 2AC² + BC².
उपपत्ति : समकोण त्रिभुजों ADB और ADC में,
AB² = AD² + BD²;
AC² = AD²+ DC²
[पाइथागोरस प्रमेय से]
AB² – AC² = BD² – DC²
= 9CD² – CD²;
[∵ BD = 3CD]
= 8CD² = 8 (\(\frac{BC}{4}\))²
[∵ BC = DB + CD
= 3CD + CD
= 4CD ]
[∴ CD = \(\frac{1}{4}\) BC]
∴ AB² – AC² = \(\frac{\mathrm{BC}^{2}}{2}\)
⇒ 2(AB²– AC²) = BC²
⇒ 2AB² – 2AC² = BC²
∴ 2AB² = 2AC² + BC².

प्रश्न 15.
किसी समबाहु त्रिभुज ABC की भजा BC पर एक बिंदु D इस प्रकार स्थित है कि BD = \(\frac{1}{3}\) BC है। सिद्ध कीजिए कि 9AD² = 7AB² है।
हल :
दिया है : समबाहु त्रिभुज ABC की भुजा BC पर एक बिंदु D इस प्रकार स्थित है कि BD = \(\frac{1}{3}\) BC.
सिद्ध करना है : 9AD² = 7AB².

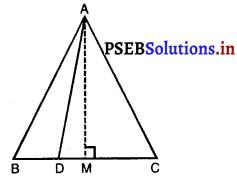
रचना : AB ⊥ BC.
उपपत्ति :- ∆AMB ≅ ∆AMC [R.H.S. नियम से क्योंकि AM = AM और AB = AC]
∴ BM = MC = \(\frac{1}{2}\) BC
पुन: {BD = \(\frac{1}{3}\) BC और DC = \(\frac{2}{3}\) BC}
(∵ BC, D पर तीन भागों में विभाजित है)
अब ∆ADC में, ∠ C न्यून कोण है। .
AD² = AC² + DC² – 2DC × MC
= AC² + (\(\frac{2}{3}\) BC)² – 2 (\(\frac{2}{3}\) BC) \(\frac{1}{2}\) BC

[∵ DC = \(\frac{2}{3}\) BC और MC = \(\frac{2}{3}\) BC]
= AB² + \(\frac{4}{9}\) AB² – \(\frac{2}{3}\) AB²
[∵ AC = BC = AB]
=\(\left(1+\frac{4}{9}-\frac{2}{3}\right)\) AB²

= \(\left(\frac{9+4-6}{9}\right)\) AB²

= \(\frac{7}{9}\) AB²

∴ AD² = \(\frac{7}{9}\) AB²

⇒ 9AD² = 7AB².

प्रश्न 16.
किसी समबाहु त्रिभुज में, सिद्ध कीजिए कि उसकी एक भुजा के वर्ग का तिगुना उसके एक शीर्षलंब के वर्ग के चार गुने के बराबर होता है।
हल :
दिया है : ∆ABC एक समबाहु A है जिसमें AB = BC = AC

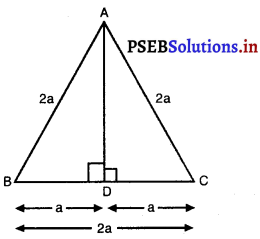
AD ⊥ DC सिद्ध करना है : 3AB² = 4AD²
उपपत्ति : ∆ABC में, मान लीजिए AB = BC = AC = 2a
AD ⊥ BC
∴ BD = DC = \(\frac{1}{2}\) BC = a समकोण त्रिभुज में,
AB² = AD² + BD²
(2a)² = AD² + (a)²
4a² = AD² + a²
4a² – a² = AD²
AD² = 3a²
= \(\left[\frac{A B}{2}\right]^{2}\)
[∵ AB = 2a, a = \(\frac{A B}{2}\)]
AD² = 3 \(\frac{\mathrm{AB}^{2}}{4}\)
3AB² = 4AD².

प्रश्न 17.
सही उत्तर चुनकर उसका औचित्य दीजिए : ∆ABC में, AB = 6√3 cm, AC = 12 cm और BC = 6 cm है। कोण B है :
(A) 120°
(B) 60°
(C) 90°
(D) 45°
हल :
AC = 12 cm
AB = 6√3 cm
BC = 6 cm
AC² = (12)² = 144 cm
AB² + BC² = (6√3)² + (6)²
= 108 + 36
AB² + BC² = 144
∴ AB² + BC² = AC²
पाइथागोरस प्रमेय के विलोम से,
∆ABC में B पर समकोण है
∴ ∠B = 90°
∴ विकल्प (C) सही है।