PSEB 10th Class Maths Solutions Chapter 7 Coordinate Geometry Ex 7.4

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 7 Coordinate Geometry Ex 7.4 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 10 Maths Chapter 7 Coordinate Geometry Ex 7.4

Question 1.
Determine the ratio in which the line it + y – 4 = 0 divides the line segment joining the points A (2, – 2) and B (3, 7).
Solution:
Let line 2x + y – 4 = 0 divides the line segment joining the points A (2,- 2) and B(3, 7) at C (x, y) in the ratio k : 1

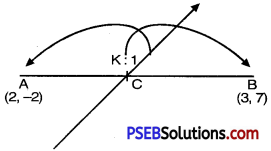
∴ Coordinates of C are x = \(\frac{3 k+2 \times 1}{k+1}=\frac{3 k+2}{k+1}\) and y = \(\frac{7 k+(-2) \times 1}{k+1}=\frac{7 k-2}{k+1}\)
∴ C \(\left[\frac{3 k+2}{k+1}, \frac{7 k-2}{k+1}\right]\). must lie on the line 2x + y – 4 = 0

i.e., 2\(\left(\frac{3 k+2}{k+1}\right)+\left(\frac{7 k-2}{k+1}\right)\) – 4 = 0
or \(\frac{6 k+4+7 k-2-4 k-4}{k+1}\) = 0
or 9k – 2 = 0
or 9k = 2
or k = \(\frac{2}{9}\).
∴ ratio k : 1 = \(\frac{2}{9}\) : 1 = 2 : 9.
Hence required ratio is 2 : 9.

Question 2.
Find a relation between x and y if (x, y) ; (1, 2) and (7, 0) are collinear.
Solution:
Let given points are A (x, y); B (1, 2) and C (7, 0).
Here x₁ = x, x₂ = 1, x₃ = 7
y₁ = y, y₂ = 2, y₃ = 0
∵ Three points are collinear
iff \(\frac{1}{2}\) [x₁ (y₂ – y₃) + x₂ (y₃ – y₁) + x₃ (y₁ – y₂)] = 0
or \(\frac{1}{2}\) x (2 – 0) + 1 (0 – y) + 7 (y – 2)] = 0
or 2x – y + 7y – 14 = 0
or 2x + 6y – 14 = 0
or x + 3y – 7 = 0 is the required relation.

Question 3.
Find the centre of a cirçle passing through the points (6, —6); (3, —7) and (3,3).
Solution:
Let O (x, y) be the required centre of the circle which passes through points P(6, – 6); Q(3, – 7) and R (3, 3).
∴ radii of circle are equal.

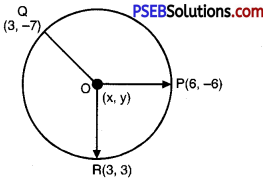
∴ OP = OQ = OR
or (OP)² = (OQ)² = (OR)²
Now, (OP)² = (OQ)²
(x – 6)² + (y + 6)² = (x – 3)² + (y + 7)²
or x² + 36 – 12x + y² + 36 + 12y = x² + 9 – 6x + y² + 49 + 14y
or – 12x + 12y + 72 = – 6x + 14y + 58
or – 6x – 2y + 14 = 0
or 3x + y – 7 = 0 ………………(1)
Also, (OQ)² = (OR)²
or (x – 3)² + (y + 7)² = (x – 3)² + (y – 3)²
or (y + 7)² = (y – 3)²
or y² + 49 + 14y = y² + 9 – 6y
or 20y = – 40
y = \(\frac{-40}{20}\) = – 2
Substitute this value of)’ in (1), we get
3x – 2 – 7 = 0
or 3x – 9 = 0
or 3x = 9
or x = \(\frac{9}{3}\) = 3
∴ Required centre is (3, – 2).

Question 4.
The two opposite vertices of a square are (- 1, 2) and (3, 2). Find the coordinates of other two vertices.
Solution:
Let two opposite vertices of a square ACBD are A (- 1, 2) and B (3, 2) and coordinates of C are (x, y)
∵ Length of each sides of square are equal.
∴ AC = BC
or (AC)² = (BC)²
or (x + 1)² + (y – 2)² = (x – 3)² + (y – 2)²

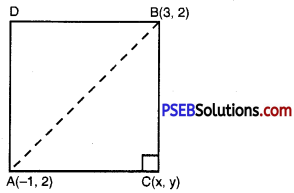
or (x + 1)² = (x – 3)²
or x² + 1 + 2x = x² + 9 – 6x
or 8x = 8
or x = \(\frac{8}{8}\) = 1
Now, in rt ∠d ∆ACB,
Using Pythagoras Theorem,
(AC)² + (BC)² = (AB)²
(x + 1)² + (y – 2)² + (x – 3)² + (y – 2)² = (3 + 1)² + (2 – 2)²
or x² + 1 + 2x + y² + 4 – 4y + x² + 9 – 6x + y² + 4 – 4y = 16
or 2x² + 2y² – 4x – 8y + 2 = 0
or x² + y² – 2x – 4y + 1 = 0
Putting the value of x = 1 in (1), we get
(1)² + y² – 2 (1) – 4y + 1 = 0
or y² – 4y = 0
or y (y – 4) = 0
Either y = 0 or y – 4 = 0
Either y = 0 or y = 4
∴ y = 0, 4
∴ Required points are (1. 0) and (1.4).

Question 5.
The Class X students of a secondary school in Krishinagar have been allotted a rectangular plot of land for their gardening activity. Sapling of Gulmohar are planted on the boundary at a distance of 1m from each other. There ¡s a triangular grassy lawn in the plot as shown in the Fig. The students are to sow seeds of flowering plants on the remaining area of the plot.

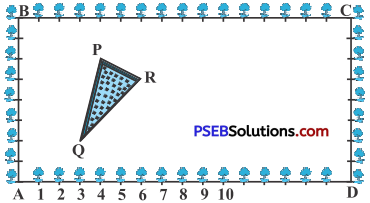
(i) Taking A as origin, find the coordinates of the vertices of the triangle.
(ii) What will be the coordinates of the vertices of A PQR if C is the origin? Also calculate the areas of the triangles In these cases. What do you observe?
Solution:
Case I:
When taking A as origin then AD is X-axis and AB is Y-axis.
∴ Coordinates of triangular grassy Lawn
PQR are P (4, 6); Q (3, 2) and R(6, 5).
Here x₁ = 4, x₂ = 3, x₃ = 6
y₁ = 6, y₂ = 2, y₃ = 50
Now, area of ∆PQR = \(\frac{1}{2}\) [x₁ (y₂ – y₃) + x₂ (y₃ – y₁) + x₃ (y₁ – y₂)]
= \(\frac{1}{2}\) [4 (2 – 5) + 3 (5 – 6) + 6 (6 – 2)]
= \(\frac{1}{2}\) [- 12 – 3 + 24] = \(\frac{9}{2}\)
= 4.5 sq. units.

Case II: When taking C as origin then CB is X – axis and CD is Y – axis.
∴ Coordinates of triangular grassy lawn PQR
are P(12, 2); Q (13,6) and R (10, 3)
Here x₁ = 12, x₂ = 13, x₃ = 10
y₁ = 2, y₂ = 6, y₃ = 3
Now, area of ∆PQR = \(\frac{1}{2}\) [x₁ (y₂ – y₃) + x₂ (y₃ – y₁) + x₃ (y₁ – y₂)]
= \(\frac{1}{2}\) [12 (6 – 3) + 13 (3 – 2) + 10 (2 – 6)]
= \(\frac{1}{2}\) [36 + 13 – 40]
= \(\frac{9}{2}\) = 4.5 sq. units.
From above two cases, it is clear that area of triangular grassy lawn is same.

Question 6.
The vertices of a ∆ABC are A (4, 6), B (1, 5) and C (7, 2). A line is drawn to intersect sides AB and AC at D and E respectively, such that \(\frac{\mathrm{AD}}{\mathrm{AB}}=\frac{\mathrm{AE}}{\mathrm{AC}}=\frac{1}{4}\) Calculate the area of the ∆ADE and compare it with the area of ∆ABC. (Recall Theorem 6.2 and Theorem 6.6).
Solution:
The vertices of ∆ABC are A (4, 6); B (1, 5) and C (7, 2)

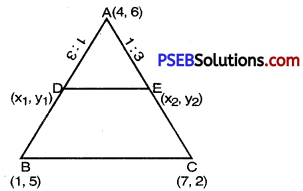
A line is drawn to intersect sides AB and AC at D (x₁, y₁) and E (x₂, y₂) respectively such that \(\frac{\mathrm{AD}}{\mathrm{AB}}=\frac{\mathrm{AE}}{\mathrm{AC}}=\frac{1}{4}\).

∴ D and E divides AB and AC in the ratio 1 : 3.
∴ Coordinates of D are
x₁ = \(\frac{1(1)+3(4)}{1+3}=\frac{1+12}{4}=\frac{13}{4}\) and y₁ = \(\frac{1(5)+3(6)}{1+3}=\frac{5+18}{4}=\frac{23}{4}\)

∴ Coordinates of D are (\(\frac{13}{4}\), \(\frac{23}{4}\))
Now, coordinates of E are
x₂ = \(\frac{1(7)+3(4)}{1+3}=\frac{7+12}{4}=\frac{19}{4}\) and y₂ = \(\frac{1(2)+3(6)}{1+3}=\frac{2+18}{4}=\frac{20}{4}=5\)

∴ Coordinates of E are (\(\frac{19}{4}\), 5).

In ∆ADE
x₁ = 4, x₂ = \(\frac{13}{4}\), x₃ = \(\frac{19}{4}\)
y₂ = 6, y₂ = \(\frac{23}{4}\), y₃ = 5
area of ∆ADE = \(\frac{1}{2}\) [x₁ (y₂ – y₃) + x₂ (y₃ – y₁) + x₃ (y₁ – y₂)]

= \(\frac{1}{2}\left[4\left(\frac{23}{4}-5\right)+\frac{13}{4}(5-6)+\frac{19}{4}\left(6-\frac{23}{4}\right)\right]\)

= \(\frac{1}{2}\left[4\left(\frac{23-20}{4}\right)+\frac{13}{4}(-1)+\frac{19}{4}\left(\frac{24-23}{4}\right)\right]\)

= \(\frac{1}{2}\left[3-\frac{13}{4}+\frac{19}{16}\right]\)

= \(\frac{1}{2}\left[\frac{48-52+19}{16}=\frac{15}{16}\right]\)
= \(\frac{15}{32}\) sq. units.

In ∆ABC
x₁ = 4, x₂ = 1, x₃ = 7
y₂ = 6, y₂ = 5, y₃ = 2
Area of ∆ABC = \(\frac{1}{2}\) [x₁ (y₂ – y₃) + x₂ (y₃ – y₁) + x₃ (y₁ – y₂)]

= \(\frac{1}{2}\) [4 (5 – 2) + 1 (2 – 6) + 7 (6 – 5)]
= \(\frac{1}{2}\) [12 – 4 + 7] = \(\frac{15}{2}\) sq.units.

Now, \(\frac{\text { area of } \Delta \mathrm{ADE}}{\text { area of } \Delta \mathrm{ABC}}=\frac{\frac{15}{32}}{\frac{15}{2}}=\frac{15}{32} \times \frac{2^{1}}{16_{1}}\)

= \(\frac{1}{16}=\left(\frac{1}{4}\right)^{2}\)

= \(\left(\frac{A D}{A B}\right)^{2} \text { or }\left(\frac{A E}{A C}\right)^{2}\).

Question 7.
Let (4, 2), B (6, 5) and C (1, 4) be the vertices of ∆ABC.
(i) The median from A meets BC at D. Find the coordinates of the point D.
(ii) Find the coordinates of the potnt P on AD such that AP : PD = 2 : 1
(iii) Find the coordinates of points Q and R on medians BE and CF respectively such that BQ : QE = 2 : 1 and CR : RF = 2 : 1.
(iv) What do you observe?
[Note : The point which is common to all the three medians ¡s called centroid and this point divides each median in the ratio 2: 1]
(v) if A (x₁, y₁), B (x₂, y₂) and C (x₃, y₃) are the vertices of ∆ABC, find the coordinates of the centroid of the triangle.
Solution:
Given that vertices of ∆ABC are A (4, 2); B (6, 5) and C (1, 4).
(i) AD is the median from the vertex A.
∴ D is the mid point of BC.

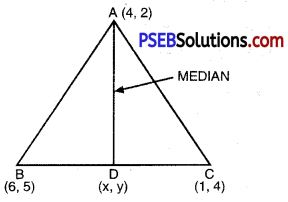
then x = \(\frac{6+1}{2}=\frac{7}{2}\) and y = \(\frac{5+4}{2}=\frac{9}{2}\)
Hence, coordinates of D is (\(\frac{7}{2}\), \(\frac{9}{2}\)).

(ii) Let P(x, y) be point on AD such that AP : PD = 2 : 1

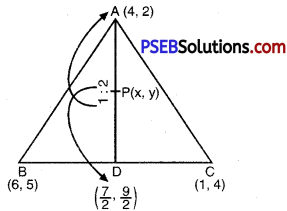
then x = \(\frac{2\left(\frac{7}{2}\right)+1(4)}{2+1}\)
= \(\frac{7+4}{3}=\frac{11}{3}\)

and y = \(\frac{2\left(\frac{9}{2}\right)+1(2)}{2+1}\)
= \(\frac{9+2}{3}=\frac{11}{3}\)

Hence, Coordinates of P is (\(\frac{11}{3}\), \(\frac{11}{3}\)).

(iii) Le BE and CF are the medians of ∆ABC to AC and AB respectively.
∴ E and F are mid points of AC and AB respectively.

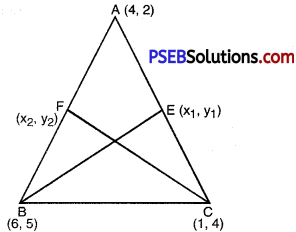
Coordinate of E are
x₁ = \(\frac{4+1}{2}=\frac{5}{2}\)
and y₁ = \(\frac{4+2}{2}=\frac{6}{2}\) = 3
Coordinate of E are (\(\frac{5}{2}\), 3)
Coordinate of F are
x₂ = \(\frac{4+6}{2}=\frac{10}{2}\) = 5
and y₂ = \(\frac{5+2}{2}=\frac{7}{2}\)
∴ Coordinate of F are (5, \(\frac{7}{2}\))
Now, Q divides BE such that BQ : QE = 2: 1

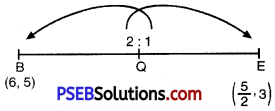
∴ Coordinate of Q are \(\left(\frac{2\left(\frac{5}{2}\right)+6(1)}{2+1}, \frac{2(3)+1(5)}{2+1}\right)\)

= \(\left(\frac{5+6}{3}, \frac{6+5}{3}\right)\) = \(\left(\frac{11}{3}, \frac{11}{3}\right)\)

Also, R divides CF such that CR : RF = 2 : 1

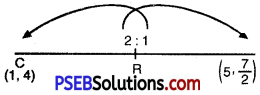
∴ Coordinate of R are = \(\left(\frac{2(5)+1(1)}{2+1}, \frac{2\left(\frac{7}{2}\right)+(4)}{2+1}\right)\)

= \(\left(\frac{10+1}{3}, \frac{7+4}{3}\right)\)

= \(\left(\frac{11}{3}, \frac{11}{3}\right)\)

(iv) From above discussion, it is clear that coordinates of P, Q and R are same and coincide at a point, is known as centroid of triangle, which divides each median in the ratio 2: 1.

(v) The vertices of given ∆ABC are
A (x₁, y₁); B (x₂, y₂) and C (x₃, y₃).

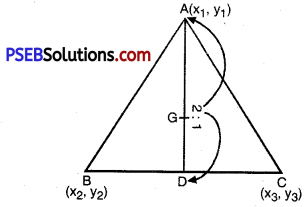
Let AD is median of E, ∆ABC.
∴ D is the mid point of BC then coordinates of D are \(\left(\frac{x_{2}+x_{3}}{2}, \frac{y_{2}+y_{3}}{2}\right)\)

Now, G be the centroid of ABC, which divides the median AD in the ratio 2: 1
∴ Coordinates of G are [using (iv)]

= \(\left[\frac{2\left(\frac{x_{2}+x_{3}}{2}\right)+1\left(x_{1}\right)}{2+1}, \frac{2\left(\frac{y_{2}+y_{3}}{2}\right)+1\left(y_{1}\right)}{2+1}\right]\)

= \(\left[\frac{x_{2}+x_{3}+x_{1}}{3}, \frac{y_{2}+y_{3}+y_{1}}{3}\right]\)

= \(\left[\frac{x_{1}+x_{2}+x_{3}}{3}, \frac{y_{1}+y_{2}+y_{3}}{3}\right]\).

Question 8.
ABCD is a rectangle formed by the points A (- 1, – 1), B (- 1, 4), C (5, 4) and D (5, – 1). P, Q R and S are the mid points
of AB, BC, CD and DA respectively. Is the quadrilateral PQRS a square ? a rectangle? or a rhombus ? Justify your answer.
Solution:
Given: The vertices ot’ given rectangle ABCD are
A(- 1, – 1); B(- 1, 4); C(5, 4) and D (5, – 1).

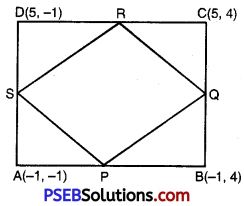
∵ P is the mid point of AB.
∴ Coordinates of P are \(\left(\frac{-1-1}{2}, \frac{-1+4}{2}\right)=\left(-1, \frac{3}{2}\right)\)
∵ Q is the mid point of BC.
∴ Co-ordinates of Q are \(\left(\frac{-5+5}{2}, \frac{4+4}{2}\right)\) = (2, 4)
∵ R is the mid point of CD.
∴ Coordinates of R are \(\left(\frac{5+5}{2}, \frac{4+1}{2}\right)=\left(5, \frac{3}{2}\right)\)

∵ S is the mid point of AD.
∴ Co-ordinates of S are \(\left(\frac{5-1}{2}, \frac{-1-1}{2}\right)\) = (2, -1)

PQ = \(\sqrt{(2+1)^{2}+\left(4-\frac{3}{2}\right)^{2}}\)

= \(\sqrt{9 \times \frac{25}{4}}=\sqrt{\frac{36+25}{4}}\)

PQ = \(\sqrt{\frac{61}{4}}\)

QR = \(\sqrt{(5-2)^{2}+\left(\frac{3}{2}-4\right)^{2}}\)

= \(\sqrt{(3)^{2}+\left(\frac{3-8}{2}\right)^{2}}\)

= \(\sqrt{9+\frac{25}{4}}=\sqrt{\frac{36+25}{4}}\)

QR = \(\sqrt{\frac{61}{4}}\)

RS = \(\sqrt{(2-5)^{2}+\left(-1-\frac{3}{2}\right)^{2}}\)

= \(\sqrt{9+\frac{25}{4}}=\sqrt{\frac{36+25}{4}}\)

RS = \(\sqrt{\frac{61}{4}}\)

and SP = \(\sqrt{(-1-2)^{2}+\left(\frac{3}{2}+1\right)^{2}}\)

SP = \(\sqrt{9+\frac{25}{4}}=\sqrt{\frac{61}{4}}\)

Also PR = \(\sqrt{(5+1)^{2}+\left(\frac{3}{2}-\frac{3}{2}\right)^{2}}\)
PR = \(\sqrt{36+0}=\sqrt{36}\) = 6
QS = \(\sqrt{(2-2)^{2}+(4+1)^{2}}\)
= \(\sqrt{0+25}=\sqrt{25}\) = 5.

Form above discussion it is clear that PQ = QR = RS = SP.
Also, PR ≠ QS.
⇒ All sides of quad. PQRS are equal but their diagonals are not equal.
Quad. PQRS is a rhombus.