PSEB 10th Class Maths Solutions Chapter 8 Introduction to Trigonometry Ex 8.1

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 8 Introduction to Trigonometry Ex 8.1 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 10 Maths Chapter 8 Introduction to Trigonometry Ex 8.1

Question 1.
In ∆ABC, right angled at B, AB = 24 cm; BC = 7 cm. Determine
(i) sin A, cos A
(ii) sin C, cos C.
Solution:
(i) We are to find sin A .cos A AB = 24 cm; BC = 7 cm
By using Pythagoras Theorem,

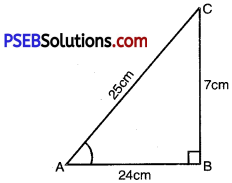
AC² = AB² + BC²
AC² = (24)² + (7)²
AC² = 576 + 49
AC² = 625
AC = \(\sqrt{625}\)
AC = 25 cm.
sin A = \(\frac{\mathrm{BC}}{\mathrm{AC}}\)

sin A = \(\frac{7 \mathrm{~cm}}{25 \mathrm{~cm}}=\frac{7}{25}\)

cos A = \(\frac{\mathrm{AB}}{\mathrm{AC}}=\frac{24 \mathrm{~cm}}{25 \mathrm{~cm}}\)

cos A = \(\frac{24}{25}\)

Hence sin A = \([latex]\frac{7}{25}\)[/latex] and cos A = \([latex]\frac{24}{25}\)[/latex].

(ii) sin C = \(\frac{\mathrm{AB}}{\mathrm{AC}}=\frac{24 \mathrm{~cm}}{25 \mathrm{~cm}}\)

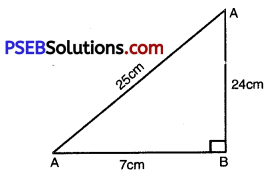
sin C = \(\frac{24}{25}\)

cos C = \(\frac{\mathrm{BC}}{\mathrm{AC}}=\frac{7 \mathrm{~cm}}{25 \mathrm{~cm}}\)

cos C = \(\frac{7}{25}\)

Hence sin C = \(\frac{24}{25}\) and cos C = \(\frac{7}{25}\).

Question 2
In fig., find tan P – cot R.

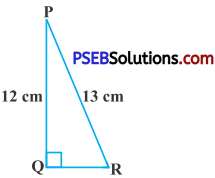
Solution:
Hyp. PR = 13 cm

By using Pythagoras Theorem,
PR² = PQ² + QR²
or (13)² = (12)² + QR²
or 169 = 144 + (QR)²
or 169 – 144 = (QR)²
or 25 = (QR)²
or QR = ± \(\sqrt{25}\)
or QR = 5, – 5.
But QR = 5 cm.
[QR ≠ – 5, because side cannot be negative]
tan P = \(\frac{R Q}{Q P}=\frac{5}{12}\)

cot R = \(\frac{R Q}{P Q}=\frac{5}{12}\)

∴ tan P – cot R = \(\frac{5}{12}-\frac{5}{12}\) = 0
Hence tan P – cot R = 0.

Question 3.
If sin A = \(\frac{3}{4}\) calculate cos A and tan A.
Solution:
Let ABC be any triangle with right angle at B.

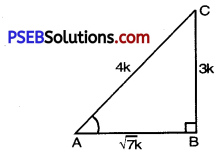
sin A = \(\frac{3}{4}\)
But sin A = \(\frac{\mathrm{BC}}{\mathrm{AC}}\) [From figure]
∴ \(\frac{\mathrm{BC}}{\mathrm{AC}}=\frac{3}{4}\)
But \(\frac{\mathrm{BC}}{\mathrm{AC}}=\frac{3}{4}\) = K
where K, is constant of proportionality.
⇒ BC = 3K, AC = 4K
By using Pythagoras Theorem,
AC² = AB² + BC²
or (4K)² = (AB)² + (3K)²
or 16K² = AB² + 9K²
or 16K² – 9K² = AB²
or 7K² = AB²
or AB = ± \(\sqrt{7 K^{2}}\)
or AB = ± \(\sqrt{7} \mathrm{~K}\)
[AB ≠ \(\sqrt{7 K}\) because side of a triangle cannot be negative]

⇒ AB = \(\sqrt{7} \mathrm{~K}\)
cos A = \(\frac{\mathrm{AB}}{\mathrm{AC}}\)
cos A = \(\frac{\sqrt{7} K}{4 K}=\frac{\sqrt{7}}{4}\)
tan A = \(\frac{\mathrm{BC}}{\mathrm{AB}}=\frac{3 \mathrm{~K}}{\sqrt{7} \mathrm{~K}}=\frac{3}{\sqrt{7}}\)

Hence cos A = \(\frac{\sqrt{7}}{4}\) and tan A = \(\frac{3}{\sqrt{7}}\).

Question 4.
Given 15 cot A = 8, find sin A and sec A.
Solution:
Let ABC be any right angled triangle where A is an acute angle with right angle at B.

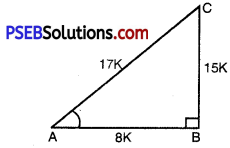
15 cot A = 8
cot A = \(\frac{8}{15}\)
But cot A = \(\frac{A B}{B C}\) (fromfig.)
⇒ \(\frac{A B}{B C}=\frac{8}{15}\) = K
where K is constant of proportionality.
AB = 8 K, BC = 15 K
By using Pythagoras Theorem.
AC² = (AB)² + (BC)²
(AC)² = (8 K)² + (15 K)²
(AC)² = 64K² + 225 K²
(AC)² = 289 K²
AC = ± \(\sqrt{289 K^{2}}\)
AC = ± 17 K
⇒ AC = 17K
[AC = – 17 K, Because side cannot be negative]
sin A = \(\frac{\mathrm{BC}}{\mathrm{AC}}=\frac{15 \mathrm{~K}}{17 \mathrm{~K}}=\frac{15}{17}\)

sin A = \(\frac{15}{17}\)

sec A = \(\frac{\mathrm{AC}}{\mathrm{AB}}\)

sec A = \(\frac{17 \mathrm{~K}}{8 \mathrm{~K}}=\frac{17}{8}\)

sec A = \(\frac{17}{8}\)

Hence, sin A = \(\frac{15}{17}\) and sec A = \(\frac{17}{8}\).

Question 5.
Given sec θ = \(\frac{13}{2}\), calculate all other trigonometric ratios.
Solution:
Let ABC be any right angled triangle with right angle at B.
Let ∠BAC = θ

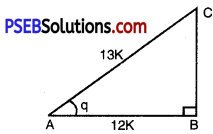
sec θ = \(\frac{13}{12}\)

But sec θ = \(\frac{\mathrm{AC}}{\mathrm{AB}}\) ……….[from fig.]

\(\frac{\mathrm{AC}}{\mathrm{AB}}=\frac{13}{12}\)

But \(\frac{\mathrm{AC}}{\mathrm{AB}}=\frac{13}{12}\) = k where k is constant of proportionality.
AC = 13 k and AB = 12 k
By using Pythagoras Theorem,
AC² = (AB)² + (BC)²
or (13k)² = (12k)² + (BC)²
or 169k² = 144k² + (BC)²
or 169k² – 144k² = (BC)
or (BC)² = 25k²
or BC = ± \(\sqrt{25 k^{2}}\)
or BC = ± 5k
or BC = 5k.
[BC ≠ – 5k because side cannot be negative]

sin θ = \(\frac{\mathrm{BC}}{\mathrm{AC}}=\frac{5 k}{13 k}=\frac{5}{13}\)
cos θ = \(\frac{\mathrm{AB}}{\mathrm{AC}}=\frac{12 k}{13 k}=\frac{12}{13}\)
tan θ = \(\frac{\mathrm{BC}}{\mathrm{AB}}=\frac{5 k}{12 k}=\frac{5}{12}\)
cosec θ = \(\frac{\mathrm{AC}}{\mathrm{BC}}=\frac{13 k}{5 k}=\frac{13}{5}\)
cot θ = \(\frac{\mathrm{AB}}{\mathrm{BC}}=\frac{12 k}{5 k}=\frac{12}{5}\).

Question 6.
If ∠A and ∠B are acute angles such that cos A = cos B, show that LA = LB.
Solution:
Let ABC be any triangle, where ∠A and ∠B are acute angles. To find cos A and cos B.

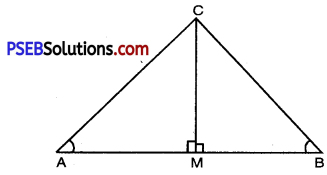
Draw CM ⊥ AB
∠AMC = ∠BMC = 90°
In right angled ∆AMC,
\(\frac{\mathrm{AM}}{\mathrm{AC}}\) = cos A ……………(1)
In right angled ∆BMC,
\(\frac{\mathrm{BM}}{\mathrm{BC}}\) = cos B ……………(2)
But cos A = cos B [given] ………..(3)
From (1), (2) and (3),
\(\frac{\mathrm{AM}}{\mathrm{AC}}=\frac{\mathrm{BM}}{\mathrm{BC}}\)
\(\frac{\mathrm{AM}}{\mathrm{BM}}=\frac{\mathrm{AC}}{\mathrm{BC}}=\frac{\mathrm{CM}}{\mathrm{CM}}\)
∴ ∆AMC = ∆BMC [By SSS similarity]
⇒ ∠A = ∠B [∵ Corresponding angles of two similar triangles are equal].

Question 7.
If cot θ = \(\frac{7}{8}\) evaluate
(i) \(\frac{(1+\sin \theta)(1-\sin \theta)}{(1+\cos \theta)(1-\cos \theta)}\)
(ii) cot² θ.
Solution:
(i) ∠ABC = θ.
In right angled triangle ABC with right angle at C.

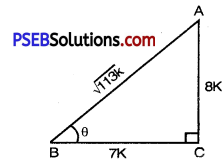
Given that, cot θ = \(\frac{7}{8}\)
But cot θ = \(\frac{\mathrm{BC}}{\mathrm{AC}}\) [From fig.]
⇒ \(\frac{\mathrm{BC}}{\mathrm{AC}}=\frac{7}{8}\)
Let \(\frac{\mathrm{BC}}{\mathrm{AC}}=\frac{7}{8}\) = k
where k is constant of proportionality.
⇒ BC = 7k, AC = 8k
By using Pythagoras Theorem,
AB² = (BC)² + (AC)²
or (AB)² = (7k)² + (8k)²
or (AB)² = 49k² + 64k²
or (AB)² = 113 k²
or AB = ± \(\)
AB = \(\sqrt{113 k^{2}}\) k
AB = \(\sqrt{113}\) k
[AB ≠ \(\sqrt{113}\) k because side cannot be negative]

sin θ = \(\frac{\mathrm{AC}}{\mathrm{AB}}=\frac{8 k}{\sqrt{113} k}\)
sin θ = \(\frac{8}{\sqrt{113}}\)
cos θ = \(\frac{\mathrm{BC}}{\mathrm{AB}}=\frac{7 k}{\sqrt{113} k}=\frac{7}{\sqrt{113}}\)
cos θ = \(\frac{7}{\sqrt{113}}\)

(1 + sin θ) (1 – sin θ) = (1 + \(\frac{8}{\sqrt{113}}\)) (1 – \(\frac{8}{\sqrt{113}}\))
= (1)² – (\(\frac{8}{\sqrt{113}}\))²
[By using formula (a + b) (a – b) = a² – b²]
= 1 – \(\frac{64}{113}\)
(1 + sin θ) (1 – sin θ) = \(\frac{113-64}{113}=\frac{49}{113}\)
(1 + sin θ)(1 – sin θ) = \(\frac{49}{113}\) ……………..(1)

(1 + cos θ) (1 – cos θ) = (1 + \(\frac{8}{\sqrt{113}}\)) (1 – \(\frac{8}{\sqrt{113}}\))
(1)² – (\(\frac{7}{\sqrt{113}}\))²
[By using formula(a + b) (a – b) = a² – b²]
= 1 – \(\frac{49}{113}\) = \(\frac{113-49}{113}\)
(1 + cos θ) (1 – cos θ) = \(\frac{64}{113}\) ……….(2)

Consider, \(\frac{(1+\sin \theta)(1-\sin \theta)}{(1+\cos \theta)(1-\cos \theta)}=\frac{\frac{49}{113}}{\frac{64}{113}}\) [From (1) and (2)]

Hence \(\frac{(1+\sin \theta)(1-\sin \theta)}{(1+\cos \theta)(1-\cos \theta)}=\frac{49}{64}\)

(ii) cot θ = \(\frac{\mathrm{BC}}{\mathrm{AC}}=\frac{7}{8}\)
cot² θ = (cot θ)²
cot² θ= (\(\frac{7}{8}\))²
⇒ cot² θ = \(\frac{49}{64}\).

Question 8.
If 3 cot A = 4 check whether \(\frac{1-\tan ^{2} A}{1+\tan ^{2} A}\) = cos² A – sin² A or not.
Solution:
Let ABC be a right angled triangle with right angled at B.

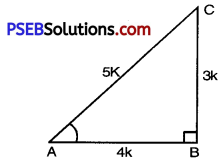
It is given that 3 cot A = 4
cot A = \(\frac{4}{3}\)
But cot A = \(\frac{\mathrm{AB}}{\mathrm{BC}}\) [From fig.]
⇒ \(\frac{A B}{B C}=\frac{4}{3}\)
But \(\frac{A B}{B C}=\frac{4}{3}\) = k
⇒ AB = 4k, BC = 3k
By using Pythagoras Theorem,
(AC)² = (AB)² + (BC)²
(AC)² = (4k)² + (3k)²
(AC)² = 16 k² + 9 k²
(AC)² = 25 k²
AC=± \(\sqrt{25 k^{2}}\)
AC = ± 5k

But AC = 5k.
[AC ≠ – 5k. because side cannot be negative]
sin A = \(\frac{\mathrm{BC}}{\mathrm{AC}}=\frac{3 k}{5 k}=\frac{3}{5}\)

tan A = \(\frac{\mathrm{BC}}{\mathrm{AB}}=\frac{3 k}{4 k}=\frac{3}{4}\)

cos A = \(\frac{\mathrm{AB}}{\mathrm{AC}}=\frac{4 k}{5 k}=\frac{4}{5}\)

L.H.S. = \(\frac{1-\tan ^{2} \mathrm{~A}}{1+\tan ^{2} \mathrm{~A}}\)

∴ cos² A – sin² A = \(\frac{7}{25}\) ………..(2)

From (1) and (2),
L.H.S = R.H.S
Hence, \(\frac{1-\tan ^{2} \mathrm{~A}}{1+\tan ^{2} \mathrm{~A}}\) = cos² A – sin² A.

Question 9.
In triangle ABC, right angled at B, if tan A = \(\frac{1}{\sqrt{3}}\). Find the value of:
(i) sin A cos C + cos A sin C
(ii) cos A cos C – sin A sin C.
Solution:
(i) Given: ABC with right angled at B

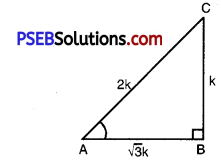
tan A = \(\frac{1}{\sqrt{3}}\) ……………..(1)
But tan A = \(\frac{B C}{A B}\) ……………(2)
From (1) and (2),
\(\frac{\mathrm{BC}}{\mathrm{AB}}=\frac{1}{\sqrt{3}}\)
Let \(\frac{\mathrm{BC}}{\mathrm{AB}}=\frac{1}{\sqrt{3}}\) = k
BC = k, AB = k
where k is constant of proportionality.
In right angled triangle ABC,
By using Pythagoras Theorem,
(AC)² = (AB)² + (BC)²
or (AC)² = (Jk)² + (k)²
or AC² = 3k² + k²
or AC² = 4k²
or AC = ± \(\sqrt{4 k^{2}}\)
AC = ± 2k.
where AC = 2k
[AC ≠ – 2k side cannot be negative]

[sin A = \(\frac{\mathrm{BC}}{\mathrm{AC}}=\frac{k}{2 k}=\frac{1}{2}\)

cos C = \(\frac{\mathrm{BC}}{\mathrm{AC}}=\frac{k}{2 k}=\frac{1}{2}\)

cos A = \(\frac{\mathrm{AB}}{\mathrm{AC}}=\frac{\sqrt{3} k}{2 k}=\frac{\sqrt{3}}{2}\)

sin C = \(\frac{\mathrm{AB}}{\mathrm{AC}}=\frac{\sqrt{3} k}{2 k}=\frac{\sqrt{3}}{2}\)] …………….(3)

sin A cos C = \(\left(\frac{1}{2}\right)\left(\frac{1}{2}\right)=\frac{1}{4}\)
cos A sin C = \(\left(\frac{\sqrt{3}}{2}\right)\left(\frac{\sqrt{3}}{2}\right)=\frac{3}{4}\)
sin A cos C + cos A sin C = \(\frac{1}{4}+\frac{3}{4}\)
= \(\frac{1+3}{4}\)
= \(\frac{4}{4}\) = 1
∴ sin A cos C + cos A sin C = 1.

(ii) cos A cos C = \(\left(\frac{\sqrt{3}}{2}\right)\left(\frac{1}{2}\right)=\frac{\sqrt{3}}{4}\) [From (3)]
sin A sin C = \(\left(\frac{1}{2}\right)\left(\frac{\sqrt{3}}{2}\right)=\frac{\sqrt{3}}{4}\) [From (3)]

cos A cos C – sin A sin C = \(\left(\frac{\sqrt{3}}{4}\right)-\left(\frac{\sqrt{3}}{4}\right)\) = 0.

Question 10.
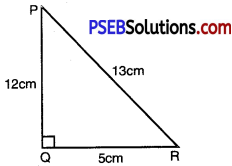
In ∆PQR, right angled at Q, PR + QR = 25 cm and PQ = 5 cm. Determine the values of sin P, cos P and tan P.
Solution:
Given: ∆PQR, right angled at Q

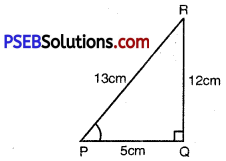
PR + QR = 25 cm
PQ = 5 cm
In right angled triangle PQR
By using Pythagoras Theorem,
(PR)² = (PQ)² + (RQ)²
or (PR)² = (5)² + (RQ)²
[∴ PR + QR = 25, QR = 25 – PR]
or (PR)² = 25 + [25 – PR]²
or (PR)² = 25 + (25)² + (PR)² – 2 × 25 × PR
or (PR)² = 25 + 625 + (PR)² – 50
or (PR)² – (PR)² + 50 PR = 650
or 50 PR = 650
or PR = \(\frac{650}{50}\)
or PR = 13 cm
QR = 25 – PR
QR = (25 – 13) cm
or QR = 12 cm.

sin P = \(\frac{Q R}{P R}=\frac{12}{13}\)

cos P = \(\frac{P Q}{P R}=\frac{5}{13}\)

tan P = \(\frac{Q R}{P Q}=\frac{12}{5}\)

Question 11.
State whether the following are true or false. Justify your answer.
(i) The value of tan A is always less than 1
(ii) sec A = \(\frac{12}{5}\) for some value of angle A.
(iii) cos A is abbreviation used for cosecant of angle A.
(iv) cot A is product of cot and A.
(v) sin θ = \(\frac{4}{3}\) for some angle θ.
Solution:
(i) False
∵ tan 60° = √3 = 1.732 > 1.

(ii) True; sec A = \(\frac{12}{5}\) = 240 > 1
∵ Sec A is always greater than 1.

(iii) False.
Because cos A is used for cosine A.

(iv) False.
Because cot A is cotangent of the angle A not the product of cot and A.

(v) False; sin θ = \(\frac{4}{3}\) = 1.666 > 1
Because sin θ is always less than 1.