PSEB 10th Class Maths Solutions Chapter 8 त्रिकोणमिति का परिचय Ex 8.1

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 8 त्रिकोणमिति का परिचय Ex 8.1 Textbook Exercise Questions and Answers

PSEB Solutions for Class 10 Maths Chapter 8 त्रिकोणमिति का परिचय Ex 8.1

प्रश्न 1.
∆ABC में, जिसका कोण B समकोण है, AB = 24 cm और BC = 7 cm है। निम्नलिखित का मान ज्ञात कीजिए।
(i) sin A, cos A
(ii) sin C, cos C.
हल :
(i) हमें ज्ञात करना है sin A, cos A
AB = 24 cm ; BC = 7 cm

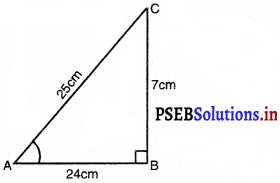
पाइथागोरस प्रमेय का प्रयोग करने पर,
AC² = AB² + BC²
AC² = (24)² + (7)²
AC² = 576 +49
AC² = 625.
AC = √625
AC = 25 cm.
sin A = \(\frac{\mathrm{BC}}{\mathrm{AC}}\)

sin A = \(\frac{7 \mathrm{~cm}}{25 \mathrm{~cm}}=\frac{7}{25}\)

sin A = \(\frac{\mathrm{AB}}{\mathrm{AC}}=\frac{24 \mathrm{~cm}}{25 \mathrm{~cm}}\)

cos A = \(\frac{24}{25}\)
अतः, sin A = \(\frac{7}{25}\) और cos A = \(\frac{24}{25}\)

(ii) sin C = \(\frac{\mathrm{AB}}{\mathrm{AC}}=\frac{24 \mathrm{~cm}}{25 \mathrm{~cm}}\)

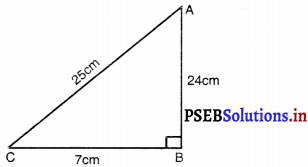
sin C = \(\frac{24}{25}\)

cos C = \(\frac{\mathrm{BC}}{\mathrm{AC}}=\frac{7 \mathrm{~cm}}{25 \mathrm{~cm}}\)

cos C = \(\frac{7}{25}\)
अतः, sin C = \(\frac{24}{25}\) और cos C = \(\frac{7}{25}\).

प्रश्न 2.
आकृति में, tan P – cot R का मान ज्ञात कीजिए।

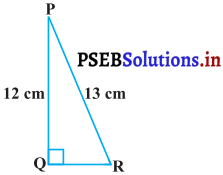
हल :
कर्ण PR = 13 cm

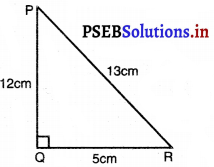
पाइथागोरस प्रमेय का प्रयोग करने पर,
PR² = PQ² + QR²
(13)² = (12)² + QR²
169 = 144 + (QR)²
या 169 – 144 = (QR)²
या 25 = (QR)²
या QR = + 125
या QR = 5, – 5.
परन्तु QR = 5 cm.
[QR ≠ – 5 क्योंकि भुजा ऋणात्मक नहीं हो सकती]
tan P = \(\frac{\mathrm{RQ}}{\mathrm{QP}}=\frac{5}{12}\)
cot R = \(\frac{\mathrm{RQ}}{\mathrm{PQ}}=\frac{5}{12}\)
∴ tan P- cot R = \(\frac{5}{12}-\frac{5}{12}\) = 0
अतः tan P – cot R = 0.

प्रश्न 3.
यदि sin A =, तो cos A और tanA का मान ज्ञात कीजिए।
हल :
मान लीजिए ABC कोई समकोण त्रिभुज है जिसमें कोण B पर समकोण है।

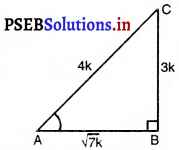
sin A = \(\frac{3}{4}\)
परन्तु sin A = \(\frac{BC}{AC}\) [आकृति से]
∴ \(\frac{\mathrm{BC}}{\mathrm{AC}}=\frac{3}{4}\)

परन्तु \(\frac{\mathrm{BC}}{\mathrm{AC}}=\frac{3}{4}\) = K

जहां K, आनुपातिकता स्थिरांक है।
BC = 3K.
AC = 4K
पाइथागोरस प्रमेय का प्रयोग करने पर
AC² = AB² + BC²
(4K)² = (AB)² + (3K)²
16K² = AB² + 9K²
या 16K² – 9K² = AB²
7K² = AB²
या AB = ± \(\sqrt{7 \mathrm{~K}^{2}}\)
AB = ± √7K
[AB ≠ ± √7K क्योंकि भुजा ऋणात्मक नहीं हो सकती]
⇒ AB = √7K
cos A = \(\frac{\mathrm{AB}}{\mathrm{AC}}\)
cos A = \(\frac{\sqrt{7} K}{4 K}=\frac{\sqrt{7}}{4}\)

tan A = \(\frac{\mathrm{BC}}{\mathrm{AB}}=\frac{3 \mathrm{~K}}{\sqrt{7} \mathrm{~K}}=\frac{3}{\sqrt{7}}\)

अत: cos A = \(\frac{\sqrt{7}}{4}\) और tan A = \(\frac{3}{\sqrt{7}}\).

प्रश्न 4.
यदि 15 cot A = 8 हो तो sin A और sec A का मान ज्ञात कीजिए।
हल :
मान लीजिए ABC कोई समकोण त्रिभुज है जिसमें A न्यून कोण है और B पर समकोण है।

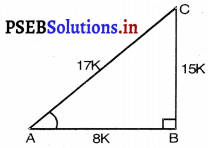
15 cot A = 8
cot A = \(\frac{8}{15}\)

परन्तु cot A = \(\frac{AB}{BC}\) [आकृति से]

⇒ \(\frac{\mathrm{AB}}{\mathrm{BC}}=\frac{8}{15}\) = K

जहां K आनुपातिकता स्थिरांक है।
⇒ AB = 8 K, BC = 15 K
पाइथागोरस प्रमेय का प्रयोग करने पर,
AC² = (AB)² + (BC)²
(AC)² = (8K)² + (15K)²
(AC)² = 64K² + 225 K²
(AC)² = 289 K²
AC = ± \(\sqrt{289 \mathrm{~K}^{2}}\)
AC = ± 17K
⇒ AC = 17K
[AC = – 17 K, क्योंकि भुजा ऋणात्मक नहीं हो सकती]

अत: sin A = \(\frac{15}{17}\) और sec A = \(\frac{17}{8}\)

प्रश्न 5.
यदि sec θ = 13 हो तो अन्य सभी त्रिकोणमितीय परिकलित अनुपात ज्ञात कीजिए।
हल :
मान लीजिए ABC कोई समकोण त्रिभुज है जिसमें B पर समकोण है।
मान लीजिए ∠BAC = θ

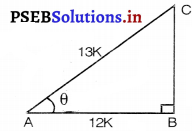
sec θ = \(\frac{13}{12}\)

परन्तु sec θ = \(\frac{AC}{AB}\) …[आकृति से]

जहां k आनुपातिकता स्थिरांक है।
AC = 13k और AB = 12k
त्रिकोणमिति का परिचय पाइथागोरस प्रमेय का प्रयोग करने पर,
AC² = (AB)² + (BC)²
(13k)² = (12k)² + (BC)²
169k²= 144k² + (BC)²
169k² – 144k² = (BC)²
(BC)² = 25k²
BC = ± \(\sqrt{25 k^{2}}\)
BC = ± 5k
BC = 5k. [BC ≠ – 5k क्योंकि भुजा ऋणात्मक नहीं हो सकती]

प्रश्न 6.
यदि ∠A और ∠B न्यून कोण हों, जहां cos A = cos B, तो दिखाइए कि ∠A = ∠B.
हल :
मान लीजिए ABC कोई त्रिभुज है जहां ∠A और ∠B न्यून कोण हैं। cos A और cos B ज्ञात करने हैं।

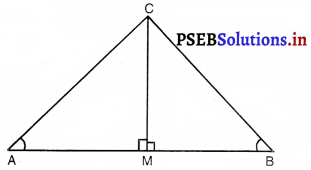
CM ⊥ AB खींचिए
∠AMC = ∠BMC = 90°
समकोण ∆AMC में,
\(\frac{\mathrm{AM}}{\mathrm{AC}}\) = cos A …………..(1)
समकोण ∆BMC में,
\(\frac{\mathrm{BM}}{\mathrm{BC}}\) = cos B …………….(2)
परन्तु cos A = cos B [दिया है। …………..(3)
(1), (2) और (3) से,
\(\frac{\mathrm{AM}}{\mathrm{AC}}=\frac{\mathrm{BM}}{\mathrm{BC}}\)
\(\frac{\mathrm{AM}}{\mathrm{BM}}=\frac{\mathrm{AC}}{\mathrm{BC}}=\frac{\mathrm{CM}}{\mathrm{CM}}\)
∴ ∆AMC ~ ∆BMC [SSS समरूपता से)
⇒ ∠A = ∠B [. क्योंकि समरूप त्रिभुजों के संगत कोण बराबर होते हैं]

प्रश्न 7.
यदि cot² θ = , तो
(i) \(\frac{(1+\sin \theta)(1-\sin \theta)}{(1+\cos \theta)(1-\cos \theta)}\)
(ii) cot² θ का मान निकालिए।
हल :
(i) ∠ABC = θ.
समकोण त्रिभुज ABC में C पर समकोण है।

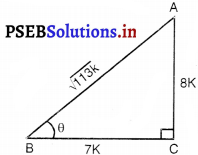
दिया है : cot θ = \(\frac{7}{8}\)
परन्तु cot θ = \(\frac{\mathrm{BC}}{\mathrm{AC}}\) [आकृति से]
\(\frac{\mathrm{BC}}{\mathrm{AC}}=\frac{7}{8}\)
मान लीजिए \(\frac{\mathrm{BC}}{\mathrm{AC}}=\frac{7}{8}\) = k
जहां k आनुपातिकता स्थिरांक है।
⇒ BC = 7k, AC = 8k
पाइथागोरस प्रमेय का प्रयोग करने से,
AB² = (BC)² + (AC)²
या (AB)² = (7k)² + (8k)²
या (AB)² = 49k² + 64k²
या (AB)² = 113k²
या AB = ± \(\sqrt{113 k^{2}}\)
AB = \(\sqrt{113}\) k
[AB ≠ – \(\sqrt{113}\) k क्योंकि भुजा ऋणात्मक नहीं हो सकती]

प्रश्न 8.
यदि 3 cot A = 4 तो जांच कीजिए कि \(\) = cos² A – sin² A है या नहीं।
हल :
मान लीजिए ABC एक समकोण त्रिभुज है जिसमें B पर समकोण है।

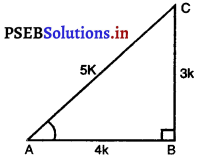
यह दिया है कि 3 cot A =4
cot A = \(\frac{4}{3}\)
परन्तु cot A = \(\frac{AB}{BC}\) [आकृति से]

\(\frac{\mathrm{AB}}{\mathrm{BC}}=\frac{4}{3}\)

परन्तु \(\frac{\mathrm{AB}}{\mathrm{BC}}=\frac{4 k}{3 k}\)
⇒ AB = 4k, BC = 3k
पाइथागोरस प्रमेय का प्रयोग करने पर,
(AC)² = (AB)² + (BC)²
(AC)² = (4k)² + (36)²
(AC)² = 16k² + 9k²
(AC)² = 25k²
AC = ± \(\sqrt{25 k^{2}}\)
AC = ± 5k
परन्तु AC = 5k. [AC ≠ – 5k, क्योंकि भुजा ऋणात्मक नहीं हो सकती]

∴ cos² A – sin² A = \(\frac{7}{25}\) …………(2)
(1) और (2) से,
L.H.S = R.H.S.
अर्थात \(\frac{1-\tan ^{2} \mathrm{~A}}{1+\tan ^{2} \mathrm{~A}}\) = cos² A – sin ²A.

प्रश्न 9.
ABC में, जिसका कोण B समकोण है, यदि tan A = \(\frac{1}{\sqrt{3}}\) तो निम्नलिखित के मान ज्ञात कीजिए।
(i) sin A cos C + cos A sin C
(ii) cos A cos C – sin A sin C.
हलः
(i) दिया है : ∆ABC जिसका कोण B समकोण | है।

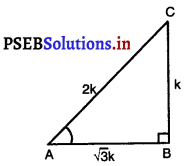
tan A = \(\frac{1}{\sqrt{3}}\) …………..(1)
परन्तु tan A = \(\frac{B C}{A B}\) ……………(2)
(1) और (2) से,
\(\frac{\mathrm{BC}}{\mathrm{AB}}=\frac{1}{\sqrt{3}}\)
मान लीजिए
\(\frac{\mathrm{BC}}{\mathrm{AB}}=\frac{1}{\sqrt{3}}\) = k
BC = k, AB = √3k
जहां k आनुपातिकता स्थिरांक है।
समकोण त्रिभुज ABC में, पाइथागोरस प्रमेय का प्रयोग करने पर,
(AC)² = (AB)² + (BC)²
(AC)² = (√3k)² + (k)²
AC² = 3k² + k²
AC² = 4k²
AC = ± \(\sqrt{4 k^{2}}\)
AC = ± 2k.
AC = 2k [AC ≠ – 2k ∵ भुजा ऋणात्मक नहीं हो सकती]

sin A cos C + cos A sin C = \(\frac{1}{4}+\frac{3}{4}\)
= \(\frac{1+3}{4}=\frac{4}{4}\) = 1
∴ sin A cos C + cos A sin C = 1.

(ii) cos A cos C = \(\left(\frac{\sqrt{3}}{2}\right)\left(\frac{1}{2}\right)=\frac{\sqrt{3}}{4}\) [(3) से

sin A sin C = \(\left(\frac{1}{2}\right)\left(\frac{\sqrt{3}}{2}\right)=\frac{\sqrt{3}}{4}\) [(3) से]

cos A cos C – sin A sin C = \(\left(\frac{\sqrt{3}}{4}\right)-\left(\frac{\sqrt{3}}{4}\right)\) = 0

प्रश्न 10.
∆PQR में, जिसका कोण Q समकोण है, PR + QR = 25 cm और PQ = 5 cm. है। sin P, cos P और tan P के मान ज्ञात कीजिए।
हल :
दिया है : ∆PQR, में Q पर समकोण है।

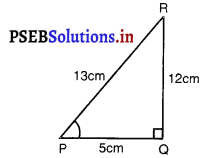
PR + QR = 25 cm
PQ = 5 cm
समकोण त्रिभुज PQR में, पाइथागोरस प्रमेय का प्रयोग करने पर,
(PR)² = (PQ)² + (RQ)²
(PR)² = (5)² + (RQ)²
[∵ PR + QR = 25
QR = 25 – PR]
या (PR)² = 25 + [25 – PR]²
या (PR)² = 25 + (25)² + (PR)² – 2×25 x PR
या (PR)² = 25+625 + (PR)² – 50 PR
या (PR)² – (PR)² + 50 PR = 650
या 50 PR = 650
PR = \(\frac{650}{50}\)
PR = 13.
QR = 25 – PR
QR = 25 – 13
QR = 12 cm.
sin P = \(\frac{\mathrm{QR}}{\mathrm{PR}}=\frac{12}{13}\)

cos P = \(\frac{\mathrm{PQ}}{\mathrm{PR}}=\frac{5}{13}\)

tan P = \(\frac{\mathrm{QR}}{\mathrm{PQ}}=\frac{12}{5}\)

प्रश्न 11.
बताइए कि निम्नलिखित कथन सत्य है या असत्य कारण सहित अपने उत्तर की पुष्टि कीजिए।
(i) tan A का मान सदैव 1 से कम होता है
(ii) कोण A के किसी मान के लिए sec A = \(\frac{12}{5}\)
(iii) cos A कोण A के cosecant के लिए प्रयुक्त एक संक्षिप्त रूप है।
(iv) cot A, cot और A का गुणनफल होता है।
(v) किसी भी कोण 8 के लिए sin θ = \(\frac{4}{3}\)
हल :
(i) असत्य
∴ tan 60° = √3 = 1.732 > 1.

(ii) सत्य
sec A = \(\frac{12}{5}\) = 2.40 > 1 (सत्य) ∵ Sec A सदैव 1 से बड़ा होता है।

(iii) असत्य
क्योंकि cos A, cosine A के लिए प्रयोग किया जाता है।

(iv) असत्य।
क्योंकि cot A, कोण A का cotangent न कि cot और A का गुणनफल।

(v) असत्य sin θ = \(\frac{4}{3}\) = 1.666 > 1 (असत्य)
क्योंकि sin θ सदैव 1 से कम होता है।