PSEB 10th Class Maths Solutions Chapter 8 ਤਿਕੋਣਮਿਤੀ ਬਾਰੇ ਜਾਣ ਪਛਾਣ Ex 8.1

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 8 ਤਿਕੋਣਮਿਤੀ ਬਾਰੇ ਜਾਣ ਪਛਾਣ Ex 8.1 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 10 Maths Chapter 8 ਤਿਕੋਣਮਿਤੀ ਬਾਰੇ ਜਾਣ ਪਛਾਣ Exercise 8.1

ਪ੍ਰਸ਼ਨ 1.
△ABC ਵਿੱਚ, ਜਿਸਦਾ ਕੋਣ B ਸਮਕੋਣ ਹੈ, AB = 24 cm ਅਤੇ BC = 7 cm ਹੈ। ਹੇਠਾਂ ਦਿੱਤਿਆਂ ਦਾ ਮੁੱਲ ਪਤਾ ਕਰੋ :
(i) sin A, cos A
(ii) sin C, cos C.
ਹੱਲ:
(i) ਅਸੀਂ ਪਤਾ ਕਰਨਾ ਹੈ sin A, cos A AB = 24 cm ; BC = 7 cm

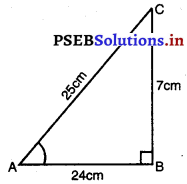
ਪਾਈਥਾਗੋਰਸ ਪ੍ਰਮੇਯ ਦਾ ਪ੍ਰਯੋਗ ਕਰਦੇ ਹੋਏ,
AC² = AB² + BC²
AC² = (24)² + (7)²
AC² = 576 + 49
AC² = 625.
AC = \(\sqrt {625}\)
AC = 25 cm.
sin A = \(\frac{BC}{AC}\)
sin A = \(\frac{7 cm}{25 cm}\) = \(\frac{7}{25}\)
cos A = \(\frac{AB}{AC}\) = \(\frac{24 cm}{25 cm}\)
cos A = \(\frac{24}{25}\)
sin A = \(\frac{7}{25}\) ਅਤੇ cos A = \(\frac{24}{25}\)

(ii) sin C = \(\frac{AB}{AC}\) = \(\frac{24 cm}{25 cm}\)

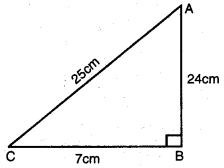
sin C = \(\frac{24}{25}\)
cos C = \(\frac{BC}{AC}\) = \(\frac{7 cm}{25 cm}\)
cos C = \(\frac{7}{25}\)
sin C = \(\frac{24}{25}\) ਅਤੇ cos C = \(\frac{7}{25}\)

ਪ੍ਰਸ਼ਨ 2.
ਚਿੱਤਰ ਵਿੱਚ, tan P – cot R ਦਾ ਮੁੱਲ ਪਤਾ ਕਰੋ ।

ਹੱਲ:
ਕਰਣ PR = 13 cm, ਲੰਬ PQ = 12 cm

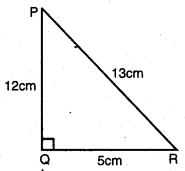
ਪਾਈਥਾਗੋਰਸ ਪ੍ਰਮੇਯ ਦਾ ਪ੍ਰਯੋਗ ਕਰਨ ‘ਤੇ,
PR² = PQ² + OR²
ਜਾਂ (13)² = (12)² + QR²
ਜਾਂ 169 = 144 + (OR)²
ਜਾਂ 169 – 144 = (QR)²
ਜਾਂ 25 = (QR)²
ਜਾਂ QR = ±\(\sqrt {25}\)
ਜਾਂ QR = 5, – 5.
ਪਰ QR = 5 cm.
[QR ≠ -5 ਕਿਉਂਕਿ ਭੁਜਾ ਰਿਣਾਤਮਕ ਨਹੀਂ ਹੁੰਦੀ]
tan P = \(\frac{RQ}{QP}\) = \(\frac{5}{12}\)
cot R = \(\frac{RQ}{PQ}\) = \(\frac{5}{12}\)
∴ tan P – cot R = \(\frac{5}{12}\) – \(\frac{5}{12}\) = 0
ਇਸ ਲਈ tan P – cot R = 0.

ਪ੍ਰਸ਼ਨ 3.
ਜੇਕਰ sin A = \(\frac{3}{4}\), ਤਾਂ cos A ਅਤੇ tan A ਦਾ ਮਾਨ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਮੰਨ ਲਉ ABC ਕੋਈ ਸਮਕੋਣ ਤ੍ਰਿਭੁਜ ਹੈ ਜਿਸ ਵਿਚ ਕੋਣ B ਸਮਕੋਣ ਹੈ ।

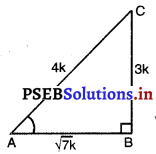
sin A = \(\frac{3}{4}\)
ਪਰ sin A = \(\frac{BC}{AC}\) [ਚਿੱਤਰ ਵਿਚ]
∴ \(\frac{BC}{AC}\) = \(\frac{3}{4}\)
ਪਰ \(\frac{BC}{AC}\) = \(\frac{3}{4}\) = k
K, ਇਕ ਸਥਿਰ ਅੰਕ ਹੈ ।
⇒ BC = 3K,
AC = 4K
ਪਾਈਥਾਗੋਰਸ ਪ੍ਰਮੇਯ ਦਾ ਪ੍ਰਯੋਗ ਕਰਕੇ,
AC² = AB² + BC²
ਜਾਂ (4K)² = (AB)² + (3K)²
ਜਾਂ 16K² = AB² + 9K²
ਜਾਂ 16K² – 9K² = AB²
ਜਾਂ 7K² = AB²
ਜਾਂ AB = ±\(\sqrt{7 \mathrm{~K}^{2}}\)
ਜਾਂ AB = ±\(\sqrt {7}\) K
[AB ≠ – 7K ਕਿਉਂਕਿ ਭੁਜਾ ਰਿਣਾਤਮਕ ਨਹੀਂ ਹੋ ਸਕਦੀ ] AB= 17 K
⇒ AB = \(\sqrt {7}\) K
cos A = \(\frac{AB}{AC}\)
cos A = \(\frac{\sqrt{7} K}{4 K}\) = \(\frac{\sqrt{7}}{4}\)
tan A = \(\frac{\mathrm{BC}}{\mathrm{AB}}\) = \(\frac{3 K}{\sqrt{7} K}\) = \(\frac{3}{\sqrt{7}}\)
∴ cos A = \(\frac{\sqrt{7}}{4}\) ਅਤੇ tan A = \(\frac{3}{\sqrt{7}}\)

ਪ੍ਰਸ਼ਨ 4.
ਜੇਕਰ 15 cot A = 8 ਹੋਵੇ ਤਾਂ sin A ਅਤੇ sec A ਦਾ ਮੁੱਲ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਮੰਨ ਲਉ ABC ਕੋਈ ਸਮਕੋਣ ਤਿਭੁਜ ਹੈ ਜਿਸ ਵਿਚ ∠A ਨਿਊਨ ਕੋਣ ਹੈ ਅਤੇ B ਸਮਕੋਣ ਹੈ ।

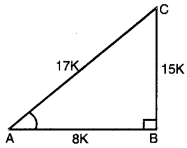
15 cot A = 8
cot A = \(\frac{8}{15}\)
ਪਰ cot A = \(\frac{AB}{BC}\) [ਚਿੱਤਰ ਵਿਚ]
⇒ \(\frac{AB}{BC}\) = \(\frac{8}{15}\) = K
K, ਸਥਿਰ ਅੰਕ ਹੈ ।
⇒ AB = 8 K, BC = 15 K
ਪਾਈਥਾਗੋਰਸ ਪ੍ਰਮੇਯ ਦਾ ਪ੍ਰਯੋਗ ਕਰਨ ‘ਤੇ
AC² = AB² + BC²
AC² = (8K)² + (15K)²
AC² = 64K² + 225 K²
AC² = 289 K²
AC = ±\(\sqrt{289 K^{2}}\)
AC = ±17K
⇒ AC = 17K
[AC = – 17 K, ਕਿਉਂਕਿ ਭੁਜਾ ਰਿਣਾਤਮਕ ਨਹੀਂ ਹੋ ਸਕਦੀ ]

ਪ੍ਰਸ਼ਨ 5.
ਜੇਕਰ sec θ = \(\frac{13}{12}\) ਹੋਵੇ ਤਾਂ ਬਾਕੀ ਸਾਰੇ ਤਿਕੋਣਮਿਤਈ ਅਨੁਪਾਤ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਮੰਨ ਲਉ ABC ਕੋਈ ਸਮਕੋਣ ਤਿਭੁਜ ਹੈ ਜਿਸ ਵਿਚ ∠B ਸਮਕੋਣ ਹੈ ।
∠BAC = θ

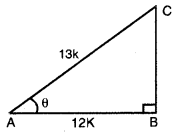
sec θ = \(\frac{13}{12}\)
ਪਰ sec θ = \(\frac{AC}{AB}\) …[ਚਿੱਤਰ ਵਿਚ]
\(\frac{AC}{AB}\) = \(\frac{13}{12}\)
ਪਰ \(\frac{AC}{AB}\) = \(\frac{13}{12}\) = k
k ਸਥਿਰ ਅੰਕ ਹੈ ।
AC = 13k ਅਤੇ AB = 12k
ਪਾਈਥਾਗੋਰਸ ਪ੍ਰਮੇਯ ਦੇ ਪ੍ਰਯੋਗ ਕਰਨ ‘ਤੇ,
AC² = (AB)² + (BC)²
ਜਾਂ (13k)² = (12k)² + (BC)²
ਜਾਂ169k² = 144k² + BC²
ਜਾਂ 169k² – 144k² = BC²
ਜਾਂ (BC)² = 25k²
ਜਾਂ BC = ±\(\sqrt{25 k^{2}}\)
ਜਾਂ BC = ±5k
ਜਾਂ BC = 5k.
[BC ≠ – 5k ਕਿਉਂਕਿ ਭੁਜਾ ਰਿਣਾਤਮਕ ਨਹੀਂ ਹੋ ਸਕਦੀ]

ਪ੍ਰਸ਼ਨ 6.
ਜੇਕਰ ∠A ਅਤੇ ∠B ਨਿਊਨ ਕੋਣ ਹੋਣ, ਜਿੱਥੇ cos A = cos B, ਤਾਂ ਦਿਖਾਉ ਕਿ ∠A = ∠B.
ਹੱਲ:
ਮੰਨ ਲਉ ABC ਕੋਈ ਤਿਭੁਜ ਹੈ ਜਿੱਥੇ ∠A ਅਤੇ ∠B ਨਿਊਨ ਕੋਣੇ ਹਨ | cos A ਅਤੇ cos B ਪਤਾ ਕਰੋ ।

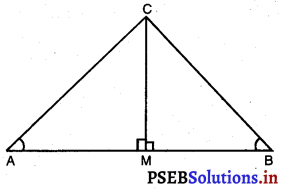
CM ⊥ AB
∠AMC : ∠BMC = 90°
ਸਮਕੋਣ △AMC ਵਿਚ,
\(\frac{AM}{AC}\) = cos A …(1)
ਸਮਕੋਣ △BMC ਵਿਚ,
\(\frac{BM}{BC}\) = cos B …(2)
ਪਰ cos A = cos B [ਦਿੱਤਾ ਹੈ ] …(3)
(1), (2) ਅਤੇ (3) ਤੋਂ,
\(\frac{AM}{AC}\) = \(\frac{BM}{BC}\)
\(\frac{AM}{BM}\) = \(\frac{AC}{BC}\) = \(\frac{CM}{CM}\)
∴ △AMC ~ △BMC [SSS ਕਸੌਟੀ ]
⇒ ∠A = ∠B [∵ ਕਿਉਂਕਿ ਸਮਰੂਪ ਤ੍ਰਿਭੁਜਾਂ ਸੰਗਤ ਕੋਣ ਬਰਾਬਰ ਹੁੰਦੇ ਹਨ]

ਪ੍ਰਸ਼ਨ 7.
ਜੇਕਰ cot θ = \(\frac{7}{8}\), ਤਾਂ
(i) \(\frac{(1+\sin \theta)(1-\sin \theta)}{(1+\cos \theta)(1-\cos \theta)}\)
(ii) cot²θ ਦਾ ਮੁੱਲ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
(i) ∠ABC = θ
ਸਮਕੋਣ ਤਿਭੁਜ ABC ਵਿਚ C ਉੱਤੇ ਸਮਕੋਣ ਹੈ ।

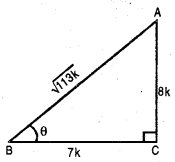
ਦਿੱਤਾ ਹੈ : cot θ = \(\frac{7}{8}\)
ਪਰ cot θ = \(\frac{BC}{AC}\) [ਚਿੱਤਰ ਵਿਚ]
⇒ \(\frac{BC}{AC}\) = \(\frac{7}{8}\)
ਮੰਨ ਲਓ \(\frac{BC}{AC}\) = \(\frac{7}{8}\) = k
ਜਿੱਥੇ k ਸਥਿਰ ਅੰਕ ਹੈ ।
⇒ BC = 7k, AC = 8k
ਪਾਈਥਾਗੋਰਸ ਪ੍ਰਮੇਯ ਦਾ ਪ੍ਰਯੋਗ ਕਰਨ ‘ਤੇ,
AB² = (BC)² + (AC)²
ਜਾਂ (AB)² = (7k)² + (8k)²
ਜਾਂ (AB)² = 49k² + 64k²
ਜਾਂ(AB)² = 113k²
ਜਾਂ AB = ±\(\sqrt{113 k^{2}}\)
AB = \(\sqrt{113}\) k
[AB ≠ –\(\sqrt{113}\) k ਕਿਉਂਕਿ ਭੁਜਾ ਰਿਣਾਤਮਕ ਨਹੀਂ ਹੋ ਸਕਦੀ]

[ਸੂਤਰ (a + b) (a – b) = a² – b² ਦਾ ਪ੍ਰਯੋਗ ਕਰਨ ‘ਤੇ]
= 1 – \(\frac{64}{113}\)
(1 + sin θ) (1 – sin θ)
= \(\frac{113-64}{113}\) = \(\frac{49}{113}\)
⇒ (1 + sin θ) (1 – sin θ) = \(\frac{49}{113}\) …(1)
(1 + cos θ) (1 – cos θ)

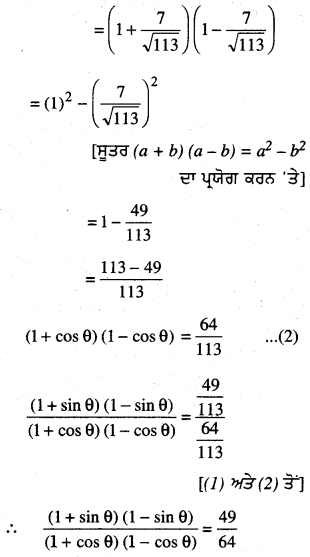
(ii) cot θ = \(\frac{BC}{AC}\) = \(\frac{7}{8}\)
cot² θ = (cot θ)²
cot² θ = \(\left(\frac{7}{8}\right)^{2}\)
⇒ cot² θ = \(\frac{49}{64}\).

ਪ੍ਰਸ਼ਨ 8.
ਜੇਕਰ 3 cot A = 4 ਤਾਂ ਪੜਤਾਲ ਕਰੋ ਕਿ \(\frac{1-\tan ^{2} A}{1+\tan ^{2} A}\) = cos²A – sin²A ਹੈ ਜਾਂ ਨਹੀਂ
ਹੱਲ:
ਮੰਨ ਲਉ ABC ਇਕ ਸਮਕੋਣ ਤ੍ਰਿਭੁਜ ਹੈ ਜਿਸ ‘ ਵਿਚ B ਸਮਕੋਣ ਹੈ ॥

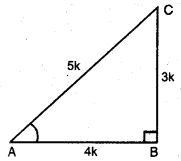
ਇਹ ਦਿੱਤਾ ਹੈ ਕਿ 3 cot A = 4
cot A = \(\frac{4}{3}\)
ਪਰ cot A = \(\frac{AB}{BC}\) [ਚਿੱਤਰ ਵਿਚੀ]
\(\frac{AB}{BC}\) = \(\frac{4}{3}\)
ਪਰ \(\frac{AB}{BC}\) = \(\frac{4k}{3k}\)
⇒ AB = 4k, BC = 3k
ਪਾਈਥਾਗੋਰਸ, ਪ੍ਰਮੇਯ ਦਾ ਪ੍ਰਯੋਗ ਕਰਨ ਤੇ,
AC² = AB² + BC²
AC² = 4k² + 3k²
AC² = 16k² + 9k²
AC² = 25²
AC = ± \(\sqrt{25 k^{2}}\)
AC = ± 5k
ਪਰ AC = 5k.
[AC ≠ – 5k, ਕਿਉਂਕਿ ਭੁਜਾ ਰਿਣਾਤਮਕ ਨਹੀਂ ਹੁੰਦੀ ਹੈ।]

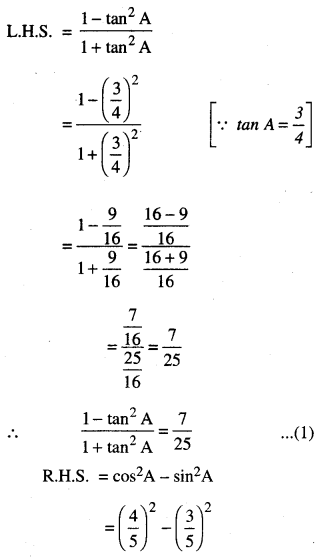
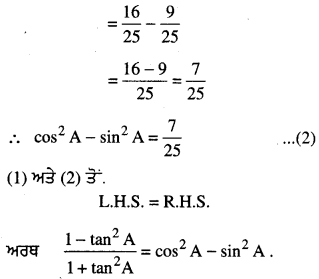
ਪ੍ਰਸ਼ਨ 9.
AABC ਵਿਚ, ਜਿਸਦਾ ਕੋਣ B ਸਮਕੋਣ ਹੈ, ਜੇਕਰ tan A = \(\frac{1}{\sqrt{3}}\), ਤਾਂ ਹੇਠਾਂ ਦਿੱਤੇ ਮੁੱਲ ਪਤਾ ਕਰੋ :
(i) sin A cos C + cos A sin C
(ii) cos A cos C – sin A sin C.
ਹੱਲ:
(i) ਦਿੱਤਾ ਹੈ : △ABC ਜਿਸਦਾ ਕੋਣ B ਸਮਕੋਣ ਹੈ ।

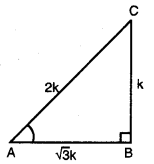
tan A = \(\frac{1}{\sqrt{3}}\) …(1)
ਪਰ tan A = \(\frac{BC}{AB}\) …(2)
(1) ਅਤੇ (2) ਤੋਂ, .
\(\frac{BC}{AB}\) = \(\frac{1}{\sqrt{3}}\)
ਮੰਨ ਲਉ \(\frac{BC}{AB}\) = \(\frac{1}{\sqrt{3}}\) = k
BC = k, AB = \(\sqrt {3}\) k
ਜਿੱਥੇ k ਸਥਿਰ ਅੰਕ ਹੈ ।
ਸਮਕੋਣ ਤ੍ਰਿਭੁਜ ABC ਵਿਚ,
ਪਾਈਥਾਗੋਰਸ ਪ੍ਰਮੇਯ ਦਾ ਪ੍ਰਯੋਗ ਕਰਨ ‘ਤੇ,
AC² = AB² + Bc²
(AC)² = ( k)² + (k)²
AC² = 3k² + k²
AC² = 4k²
AC = ± \(\sqrt{4 k^{2}}\)
AC = ± 2k.
ਇੱਥੇ AC = 2k
[AC ≠ – 2k ∵ ਭੁਜਾ ਰਿਣਾਤਮਕ ਨਹੀਂ ਹੋ ਸਕਦੀ]

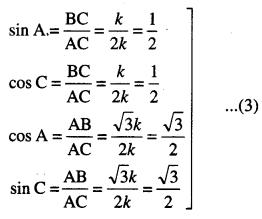
sin A cos C = \(\left(\frac{1}{2}\right)\)\(\left(\frac{1}{2}\right)\) = \(\frac{1}{4}\)
cos A sin C = \(\left(\frac{\sqrt{3}}{2}\right)\)\(\left(\frac{\sqrt{3}}{2}\right)\) = \(\frac{3}{4}\)
sin A cos C + cos A sinC
= \(\frac{1}{4}\) + \(\frac{3}{4}\)
= \(\frac{1+3}{4}\) = \(\frac{4}{4}\) = 1
∴ sin A cos C + cos A sin C = 1.

(ii) cos A cos C = \(\left(\frac{\sqrt{3}}{2}\right)\)\(\left(\frac{1}{2}\right)\) = \(\frac{\sqrt{3}}{4}\) [(3) ਤੋਂ]
sin A sin C = \(\left(\frac{1}{2}\right)\)\(\left(\frac{\sqrt{3}}{2}\right)\) = \(\frac{\sqrt{3}}{4}\) [(3) ਤੋਂ।]
cos A cos C – sin A sin C
= \(\left(\frac{\sqrt{3}}{4}\right)\) – \(\left(\frac{\sqrt{3}}{4}\right)\) = 0

ਪ੍ਰਸ਼ਨ 10.
△POR ਵਿੱਚ, ਜਿਸਦਾ ਕੋਣ Q ਸਮਕੋਣ ਹੈ, PR + QR = 25 cm ਅਤੇ PQ = 5 cm ਹੈ । sin P, cos P ਅਤੇ tan P ਦੇ ਮੁੱਲ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਦਿੱਤਾ ਹੈ : △PQR, ਵਿੱਚ Q ਸਮਕੋਣ ਹੈ ।

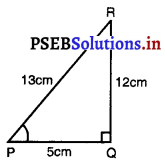
PR + QR = 25 cm
PQ = 5 cm
ਸਮਕੋਣ ਭੁਜ PQR ਵਿਚ,
ਪਾਈਥਾਗੋਰਸ ਪ੍ਰਮੇਯ ਦਾ ਪ੍ਰਯੋਗ ਕਰਨ ਤੇ,
PR² = PQ² + RQ²
ਜਾਂ PR² = 5² + RQ²
[∵ PR + OR = 25
QR = 25 – PR]
PR² = 25 + [25 – PR]²
PR² = 25 + 25² + PR² – 2 × 25 × PR PR² = 25 + 625 + PR² – 50 PR
PR² – PR² + 50 PR = 650
PR = \(\frac{650}{50}\)
PR = 13
∴ QR = 25 – PR
⇒ 25 – 13
= 12 cm.
sin P = \(\frac{QR}{PR}\) = \(\frac{12}{13}\)
cos P = \(\frac{PQ}{PR}\) = \(\frac{5}{13}\)
tan P = \(\frac{QR}{PQ}\) = \(\frac{12}{5}\)

ਪ੍ਰਸ਼ਨ 11.
ਦੱਸੋ ਕਿ ਹੇਠਾਂ ਦਿੱਤੇ ਕਥਨ ਠੀਕ ਹਨ ਜਾਂ ਗਲਤ, ਕਾਰਣ ਸਹਿਤ ਆਪਣੇ ਉੱਤਰ ਦੀ ਪੁਸ਼ਟੀ ਕਰੋ।
(i) tan A ਦਾ ਮੁੱਲ ਹਮੇਸ਼ਾ 1 ਤੋਂ ਘੱਟ ਹੁੰਦਾ ਹੈ ।
(ii) ਕੋਣ A ਦੇ ਕਿਸੇ ਮੁੱਲ ਲਈ sec A = \(\frac{12}{5}\).
(iii) cos A, ਕੋਣ A ਦੇ cosecant ਦਾ ਸੰਖੇਪ ਰੂਪ ਹੈ ।
(iv) cot A, cot ਅਤੇ A ਦਾ ਗੁਣਨਫਲ ਹੁੰਦਾ ਹੈ !
(v) ਕਿਸੇ ਵੀ ਕੋਣ 8 ਦੇ ਲਈ sin θ = \(\frac{4}{3}\).
ਹੱਲ:
(i) ਠੀਕ ਨਹੀਂ ਹੈ
∵ tan 60° = \(\sqrt {3}\) = 1.732 > 1.
(ii) ਠੀਕ ਹੈ, sec A = \(\frac{12}{5}\) = 2:40 > 1
∵ Sec A ਹਮੇਸ਼ਾਂ A ਤੋਂ ਵੱਡਾ ਹੁੰਦਾ ਹੈ ।
(ii) ਠੀਕ ਨਹੀਂ
ਕਿਉਂਕਿ cos A, cosine A ਦੇ ਲਈ ਪ੍ਰਯੋਗ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ।
(iv) ਠੀਕ ਨਹੀਂ
ਕਿਉਂਕਿ cot A, ਕੋਣ A ਦਾ cotangent ਹੈ ਨਾ ਕਿ cot ਅਤੇ A ਦਾ ਗੁਣਨਫਲ ।
(v) ਠੀਕ ਨਹੀਂ sin θ = \(\frac{4}{3}\) = 1 666 > 1
ਕਿਉਂਕਿ sin θ ਹਮੇਸ਼ਾਂ 1 ਤੋਂ ਘੱਟ ਹੁੰਦਾ ਹੈ ।