Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 8 ਤਿਕੋਣਮਿਤੀ ਬਾਰੇ ਜਾਣ ਪਛਾਣ Ex 8.2 Textbook Exercise Questions and Answers.
PSEB Solutions for Class 10 Maths Chapter 8 ਤਿਕੋਣਮਿਤੀ ਬਾਰੇ ਜਾਣ ਪਛਾਣ Exercise 8.2
ਪ੍ਰਸ਼ਨ 1.
ਹੇਠ ਲਿਖਿਆਂ ਦੇ ਮੁੱਲ ਪਤਾ ਕਰੋ :
(i) sin 60° cos 30° + sin 30° cos 60°
(ii) 2 tan2 45° + cos2 30° – sin2 60°
(iii) \(\frac{\cos 45^{\circ}}{\sec 30^{\circ}+{cosec} 30^{\circ}}\)
(iv) \(\frac{\sin 30^{\circ}+\tan 45^{\circ}-{cosec} 60^{\circ}}{\sec 30^{\circ}+\cos 60^{\circ}+\cot 45^{\circ}}\)
(v) \(\frac{5 \cos ^{2} 60^{\circ}+4 \sec ^{2} 30^{\circ}-\tan ^{2} 45^{\circ}}{\sin ^{2} 30^{\circ}+\cos ^{2} 30^{\circ}}\)
ਹੱਲ:
(i) ਦਿੱਤਾ ਹੈ :
sin 60° cos 30° + sin 30° cos 60°
= \(\left(\frac{\sqrt{3}}{2}\right)\)\(\left(\frac{\sqrt{3}}{2}\right)\) + \(\left(\frac{1}{2}\right)\)\(\left(\frac{1}{2}\right)\)
= \(\left(\frac{\sqrt{3}}{2}\right)^{2}\) + \(\left(\frac{1}{2}\right)^{2}\)
= \(\frac{3}{4}\) + \(\frac{1}{4}\) = 1.
(ii) ਦਿੱਤਾ ਹੈ :
2 tan2 45° + cos2 30° – sin2 60°
= 2 (tan 45°)2 + (cos 30°)2 – (sin 60°)2
= 2(1)2 + \(\left(\frac{\sqrt{3}}{2}\right)^{2}\) – \(\left(\frac{\sqrt{3}}{2}\right)^{2}\) = 2.
(iii) ਦਿੱਤਾ ਹੈ : \(\frac{\cos 45^{\circ}}{\sec 30^{\circ}+{cosec} 30^{\circ}}\)

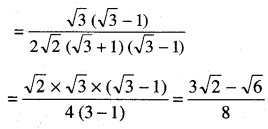
(iv) ਦਿੱਤਾ ਹੈ : \(\frac{\sin 30^{\circ}+\tan 45^{\circ}-{cosec} 60^{\circ}}{\sec 30^{\circ}+\cos 60^{\circ}+\cot 45^{\circ}}\)
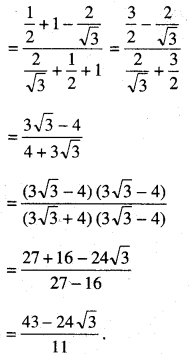
(v) ਦਿੱਤਾ ਹੈ : \(\frac{5 \cos ^{2} 60^{\circ}+4 \sec ^{2} 30^{\circ}-\tan ^{2} 45^{\circ}}{\sin ^{2} 30^{\circ}+\cos ^{2} 30^{\circ}}\)
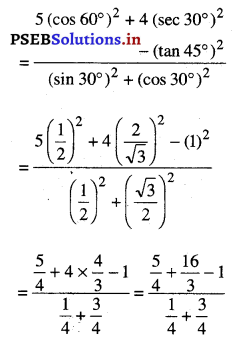
= \(\frac{5}{4}\) + \(\frac{16}{3}\) – 1 = \(\frac{15+64-12}{12}\)
= \(\frac{67}{12}\).
![]()
2. ਸਹੀ ਉੱਤਰ ਚੁਣੋ ਅਤੇ ਉਸਦਾ ਕਾਰਣ ਦੱਸੋ :
ਪ੍ਰਸ਼ਨ (i).
\(\frac{2 \tan 30^{\circ}}{1+\tan ^{2} 30^{\circ}}\)
(A) sin 60°
(B) cos 60°
(C) tan 60°
(D) sin 30°
ਉੱਤਰ:
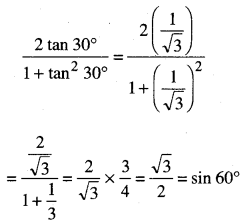
∴ ਵਿਕਲਪ ‘A’ ਸਹੀ ਹੈ ।
ਪ੍ਰਸ਼ਨ (ii).
\(\frac{1-\tan ^{2} 45^{\circ}}{1+\tan ^{2} 45^{\circ}}\)
(A) tan 90°
(B) 1
(C) sin45°
(D) 0.
ਉੱਤਰ:
\(\frac{1-\tan ^{2} 45^{\circ}}{1+\tan ^{2} 45^{\circ}}\) = \(\frac{1-(1)^{2}}{1+(1)^{2}}\) = 0.
∴ ਵਿਕਲਪ “D’ ਸਹੀ ਹੈ ।
ਪ੍ਰਸ਼ਨ (iii).
sin2A = 2sin A ਉਦੋਂ ਸੱਚ ਹੁੰਦਾ ਹੈ, ਜਦੋਂ A ਬਰਾਬਰ ਹੈ :
(A) 0°
(B) 30°
(C) 450
(D) 60°
ਉੱਤਰ:
ਦਿੱਤਾ ਹੈ, sin 2A = 2 sin A
ਜਦੋਂ, A = 0° ਹੋਵੇ ਤਾਂ
sin 2(0) = 2 sin 0
sin 0 = 0
0 = 0; ਜੋ ਸੱਚ ਹੈ ।
∴ ਵਿਕਲਪ ‘A’ ਸਹੀ ਹੈ ।
ਪ੍ਰਸ਼ਨ (iv).
\(\frac{2 \tan 30^{\circ}}{1-\tan ^{2} 30^{\circ}}\) ਬਰਾਬਰ ਹੈ :
(A) cos 60°
(B) sin 60°
(C) tan 60°
(D) sin 30°.
ਉੱਤਰ:

∴ ਵਿਕਲਪ ‘C’ ਸਹੀ ਹੈ ।
![]()
ਪ੍ਰਸ਼ਨ 3.
ਜੇਕਰ tan (A + B) = \(\sqrt {3}\) ਅਤੇ tan (A – B) = \(\frac{1}{\sqrt{3}}\); 0° < A + B ≤ 90° ; A > B ਤਾਂ A ਅਤੇ B ਦਾ ਮੁੱਲ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
tan (A + B) = \(\sqrt {3}\)
tan (A + B) = tan 60°
⇒ A + B = 60° …(1)
tan (A – B) = \(\frac{1}{\sqrt{3}}\)
ਜਾਂ tan (A – B) = tan 30°
⇒ A – B = 30° …(2)
(1) ਅਤੇ (2) ਜੋੜਨ ‘ਤੇ
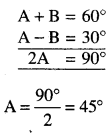
A = 45°
(1) ਵਿਚ ਮੁੱਲ ਭਰਨ ‘ਤੇ
45° + B = 60°
B = 60° – 45°
B = 15°
∴ A = 45° ਅਤੇ B = 15°
ਪ੍ਰਸ਼ਨ 4.
ਦੱਸੋ ਹੇਠਾਂ ਦਿੱਤਿਆਂ ਵਿੱਚੋਂ ਕਿਹੜਾ ਸਹੀ ਹੈ ਅਤੇ ਕਿਹੜਾ ਗਲਤ। ਕਾਰਣ ਸਹਿਤ ਆਪਣੇ ਉੱਤਰ ਦੀ ਪੁਸ਼ਟੀ ਕਰੋ।
(i) sin (A + B) = sin A + sin B.
(ii) θ ਦੇ ਵੱਧਣ ਨਾਲ sin θ ਦਾ ਮੁੱਲ ਵੀ ਵਧਦਾ ਹੈ।
(iii) θ ਦੇ ਵੱਧਣ ਨਾਲ cos θ ਦਾ ਮੁੱਲ ਵੀ ਵਧਦਾ ਹੈ।
(iv) θ ਦੇ ਸਾਰੇ ਮੁੱਲਾਂ ਲਈ sin θ = cos θ.
(v) A = 0° ਤੇ cot A ਪਰਿਭਾਸ਼ਿਤ ਨਹੀਂ ਹੈ ।
ਹੱਲ:
(i) ਠੀਕ ਨਹੀਂ
ਜਦੋਂ A = 60°, B = 30°
L.H.S. = sin (A + B)
= sin (60° + 30°)
= sin 90° = 1
R.H.S. = sin A + sin B
= sin 60° + sin 30°
= \(\frac{\sqrt{3}}{2}\) + \(\frac{1}{2}\) ≠ 1
ਅਰਥ L.H.S. ≠ R.H.S.
(ii) ਠੀਕ ਹੈ sin 30° = \(\frac{1}{2}\) = 0.5,
ਕਿਉਂਕਿ, sin 45 = \(\frac{1}{\sqrt{2}}\) = 0.7 (ਲਗਭਗ )
sin 60° = \(\frac{\sqrt{3}}{2}\) = 0.87 (ਲਗਭਗ)
ਅਤੇ sin 90° = 1
ਅਰਥ, ਜਦੋਂ θ ਦਾ ਮੁੱਲ 0° ਤੋਂ 90° ਤਕ ਵਧਦਾ ਹੈ ਤਾਂ sin 6 ਦਾ ਮੁੱਲ ਵੀ ਵਧਦਾ ਹੈ ।
![]()
(iii) ਠੀਕ ਨਹੀਂ
ਕਿਉਂਕਿ cos 0° = 1,
cos 30° = \(\frac{\sqrt{3}}{2}\) = 0.87 (ਲਗਭਗ) ।
cos 45° = \(\frac{1}{\sqrt{2}}\) = 0.7 (ਲਗਭਗ)
cos 60°= \(\frac{1}{2}\) = 0.5
ਅਤੇ cos 90° = 0.
ਜਦੋਂ θ ਦਾ ਮੁੱਲ 0° ਤੋਂ 90° ਤੱਕ ਵਧਦਾ ਹੈ ਤਾਂ cos 9 ਦਾ ਮੁੱਲ ਘਟਦਾ ਹੈ ।
(iv) ਠੀਕ ਨਹੀਂ
ਕਿਉਂਕਿ sin 30° = \(\frac{1}{2}\)
ਅਤੇ cos 30° = \(\frac{\sqrt{3}}{2}\)
ਜਾਂ sin 30° ≠ cos 30°
ਸਾਨੂੰ ਮਿਲਦਾ ਹੈ :
sin 45° = cos 45°.
\(\frac{1}{\sqrt{2}}\) = \(\frac{1}{\sqrt{2}}\)
![]()
(v) ਠੀਕ ਹੈ
cot 0°= \(\frac{1}{\tan 0^{\circ}}\) = \(\frac{1}{0}\), ਜਾਂ ਪਰਿਭਾਸ਼ਿਤ ਨਹੀਂ ।
