PSEB 10th Class Maths Solutions Chapter 8 Introduction to Trigonometry Ex 8.4

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 8 Introduction to Trigonometry Ex 8.4 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 10 Maths Chapter 8 Introduction to Trigonometry Ex 8.4

Question 1.
Express the trigonometric ratios of sin A, sec A and tan A in terms of cot A.
Solution:
By using Identity,
cosec² A – cot² A = 1
⇒ cosec² A = 1 + cot² A
⇒ (cosec A)² = cot² A + 1
⇒ \(\left(\frac{1}{\sin A}\right)^{2}\) = cot² A + 1
⇒ (sin A)² = \(\frac{1}{\cot ^{2} \mathrm{~A}+1}\)
⇒ sin A = ± \(\frac{1}{\sqrt{\cot ^{2} \mathrm{~A}+1}}\)
We reject negative values of sin A for acute angle A.
Therefore, sin A = \(\frac{1}{\sqrt{\cot ^{2} A+1}}\)
By using identity,
sec² A – tan² A = 1
⇒ sec² A = 1 + tan² A
= 1 + \(\frac{1}{\cot ^{2} A}\)
= \(\frac{\cot ^{2} A+1}{\cot ^{2} A}\)

⇒ sec A = \(\sqrt{\frac{\cot ^{2} A+1}{\cot ^{2} A}}\)

tan A = \(\frac{1}{\cot A}\).

Question 2.
Write all the other trigonometric ratios of ∠A in terms of sec A.
Solution:
By using Identity
sin² A + cos² A = 1
⇒ sin² A = 1 – cos² A
= 1 – \(\frac{1}{\sec ^{2} \cdot A}\) = \(\frac{\sec ^{2} A-1}{\sec ^{2} A}\)

⇒ (sin A)² = \(\frac{\sec ^{2} A-1}{\sec ^{2} A}\)

⇒ sin A = ± \(\sqrt{\frac{\sec ^{2} A-1}{\sec ^{2} A}}\)

[Reject – ve sign for acute angle A]
⇒ sin A = ± \(\sqrt{\frac{\sec ^{2} A-1}{\sec ^{2} A}}\)
cos A = \(\frac{1}{\sec A}\)
1 + tan² A = sec² A
tan² A = sec² A – 1
(tan A)² = sec² A – 1
⇒ tan A = ± \(\sqrt{\sec ^{2} A-1}\)
[Reject – ve sign for acute angle A]
i.e., tan A = \(\sqrt{\sec ^{2} A-1}\)
cosec A = \(\frac{1}{\sin A}=\frac{1}{\sqrt{\sec ^{2} A-1}}\)

= \(\frac{\sec A}{\sqrt{\sec ^{2} A-1}}\)

cot A = \(\frac{1}{\tan A}=\frac{1}{\sqrt{\sec ^{2} A-1}}\).

Question 3.
Evaluate:
(i) \(\frac{\sin ^{2} 63^{\circ}+\sin ^{2} 27^{\circ}}{\cos ^{2} 17^{\circ}+\cos ^{2} 73^{\circ}}\)

(ii) sin 25° cos 65° + cos 25° sin 65°.
Solution:
(i) \(\frac{\sin ^{2} 63^{\circ}+\sin ^{2} 27^{\circ}}{\cos ^{2} 17^{\circ}+\cos ^{2} 73^{\circ}}\)

= \(\frac{\left\{\sin \left(90^{\circ}-27^{\circ}\right)+\sin ^{2} 27^{\circ}\right\}}{\cos ^{2} 17^{\circ}+\left\{\cos \left(90^{\circ}-17^{\circ}\right)\right\}^{2}}\)
[∵ sin(90 – θ) = cos θ and cos (90 – θ) = sin θ]

= \(\frac{\left\{\cos 27^{\circ}\right\}^{2}+\sin ^{2} 27^{\circ}}{\cos ^{2} 17^{\circ}+\left\{\sin 17^{\circ}\right\}^{2}}\)

= \(\frac{\cos ^{2} 27^{\circ}+\sin ^{2} 27^{\circ}}{\cos ^{2} 17^{\circ}+\sin ^{2} 17^{\circ}}\)
= \(\frac{1}{1}\) = 1.

(ii) sin 25° cos 65° + cos 25° sin 65°
= sin 25° × cos (90° – 25°)
+ cos 25° × sin (90° – 25°)
[∵ cos (90° – θ) = sin θ
sin(90° – θ) = cos θ].
= sin 25° × sin 25° + cos 25° × cos 25°
= sin² 25° + cos² 25° = 1.

Question 4.
Choose the correct option. Justify your choice:
(i) 9 sec² A – 9 tan² A =
(A) 1
(B) 9
(C) 8
(D) 0.

(ii) (1 + tan θ + sec θ) (1 + cot θ – cosec θ) =
(A) θ
(B) 1
(C) 2
(D) – 1.

(iii) (sec A + tan A) (1 – sin A) =
(A) sec A
(B) sin A
(C) cosec A
(D) cos A.

(iv) \(\frac{1+\tan ^{2} A}{1+\cot ^{2} A}\) =
(A) sec²A
(B) – 1
(C) cot² A
(D) tan² A.

Solution:
(i) Consider, 9 sec² A – 9 tan² A
= 9 (sec² A – tan² A)
= 9 × 1 = 9.
Option (B) is correct.

(ii) Consider, (1 + tan θ + sec θ) (1 + cot θ – cosec θ)
= \(\left\{1+\frac{\sin \theta}{\cos \theta}+\frac{1}{\cos \theta}\right\} \times\left\{1+\frac{\cos \theta}{\sin \theta}-\frac{1}{\sin \theta}\right\}\)

= \(\left\{\frac{\cos \theta+\sin \theta+1}{\cos \theta}\right\} \times\left\{\frac{\sin \theta+\cos \theta+1}{\sin \theta}\right\}\)

= \(\begin{array}{r}
\{(\cos \theta+\sin \theta)+1\} \\
\times\{(\cos \theta+\sin \theta)-1\} \\
\hline \cos \theta \times \sin \theta
\end{array}\)

= \(\frac{(\cos \theta+\sin \theta)^{2}-(1)^{2}}{\cos \theta \times \sin \theta}\)

[∵ (a + b) (a – b) = a² – b²]

= \(\frac{\cos ^{2} \theta+\sin ^{2} \theta+2 \cos \theta \sin \theta-1}{\cos \theta \times \sin \theta}\)

= \(\frac{1+2 \cos \theta \sin \theta-1}{\cos \theta \sin \theta}\) = 2.

Option (C) is correct.

(iii) Consider, (sec A + tan A) (1 – sin A)
= \(\left(\frac{1}{\cos A}+\frac{\sin A}{\cos A}\right)\) × (1 – sin A)

= \(\frac{(1+\sin A)}{\cos A}\) × (1 – sin A)

= \(\frac{(1+\sin A)(1-\sin A)}{\cos A}\)

= \(\frac{(1)^{2}-(\sin A)^{2}}{\cos A}=\frac{1-\sin ^{2} A}{\cos A}=\frac{\cos ^{2} A}{\cos A}\)
[∵ cos² A = 1 – sin² A]
= cos A.
Option (D) is correct.

(iv) Consider, \(\frac{1+\tan ^{2} A}{1+\cot ^{2} A}\)

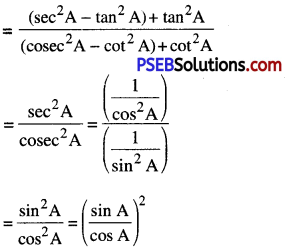
= tan² A.
Option (D) is correct.

Question 5.
Prove the following Identities, where the angles involved are acute angles for which the expressions are defined.
(i) (cosec θ – cot θ) = \(\frac{1-\cos \theta}{1+\cos \theta}\)

(ii) \(\frac{\cos A}{1+\sin A}+\frac{1+\sin A}{\cos A}\) = 2 sec A.

(iii) \(\frac{\tan \theta}{1+\cot \theta}+\frac{\cot \theta}{1-\tan \theta}\) = 1 + sec θ cosec θ
[Hint : Write the expression in terms of sin θ and cos θ]

(iv) \(\frac{1+\sec A}{\sec A}=\frac{\sin ^{2} A}{1-\cos A}\)
[Hint: Simplify L.H.S. and R.H.S. separately]

(v) \(\frac{\cos A-\sin A+1}{\cos A+\sin A-1}\) using the identity cosec² A = 1 + cot² A.

(vi) \(\sqrt{\frac{1+\sin A}{1-\sin A}}\) = sec A + tan A

(vii) \(\frac{\sin \theta-2 \sin ^{3} \theta}{2 \cos ^{3} \theta-\cos \theta}\) = tan θ

(viii) (sin A + cosec A)² + (cos A + sec A)² = 7 + tan² A + cot² A.

(ix) (cosec A – sin A) (sec A – cos A) = \(\frac{1}{\tan A+\cot A}\)
[Hint : Simplify L.H.S. and R.H.S. separately]

(x) \(\left(\frac{1+\tan ^{2} A}{1+\cot A^{2}}\right)=\left(\frac{1-\tan A}{1-\cot A}\right)^{2}\) = tan² A.

Solution:
(i) L.H.S. = (cosec θ – cot θ)²
= \(\left\{\frac{1}{\sin \theta}-\frac{\cos \theta}{\sin \theta}\right\}^{2}\)

= \(\left(\frac{1-\cos \theta}{\sin \theta}\right)^{2}=\frac{(1-\cos \theta)^{2}}{\sin ^{2} \theta}\)
Using identity, sin² θ + cos² θ = 1
⇒ sin² θ = 1 – cos² θ
= \(\frac{(1-\cos \theta)^{2}}{1-\cos ^{2} \theta}\)
= \(\)
[∵ a² – b² = (a + b) (a – b)]

= \(\)

∴ L.H.S. = R.H.S.
Hence, (cosec θ – cot θ)² = \(\frac{1-\cos \theta}{1+\cos \theta}\)

(ii) L.H.S. = \(\frac{\cos A}{1+\sin A}+\frac{1+\sin A}{\cos A}\)

= \(\frac{2}{\cos A}\) = cos A
∴L.H.S. = R.H.S.
Hence, \(\frac{\cos A}{1+\sin A}+\frac{1+\sin A}{\cos A}\) = 2 sec A.

(iii) L.H.S. = \(\frac{\tan \theta}{1+\cot \theta}+\frac{\cot \theta}{1-\tan \theta}\) = 1 + sec θ cosec θ

= \(\frac{\left(\frac{\sin \theta}{\cos \theta}\right)}{\left(1-\frac{\cos \theta}{\sin \theta}\right)}+\frac{\left(\frac{\cos \theta}{\sin \theta}\right)}{\left(1-\frac{\sin \theta}{\cos \theta}\right)}\)

= \(\frac{1+\sin \theta \cos \theta}{\cos \theta \sin \theta}=\frac{1}{\cos \theta \sin \theta}+1\)

= 1 + \(\left(\frac{1}{\cos \theta}\right)\left(\frac{1}{\sin \theta}\right)\) = 1 + sec θ cosec θ
∴L.H.S. = R.H.S.
Hence, \(\frac{\tan \theta}{1+\cot \theta}+\frac{\cot \theta}{1-\tan \theta}\) = 1 + sec θ cosec θ

(iv) L.H.S. = \(\frac{1+\sec A}{\sec A}=\frac{\sin ^{2} A}{1-\cos A}\)
= \(\frac{1+\frac{1}{\cos A}}{\frac{1}{\cos A}}\)
= 1 + cos A …………….(1)
R.H.S = \(\frac{\sin ^{2} A}{1-\cos A}\)
(∵ 1 – cos² A = sin² A.)
= \(\frac{1-\cos ^{2} A}{1-\cos A}\)

= \(\frac{(1+\cos A)(1-\cos A)}{(1-\cos A)}\)

= 1 + cos A. …………….(2)
From (1) and (2) it is clear that
∴ L.H.S. = R.H.S.
Hence, \(\frac{1+\sec A}{\sec A}=\frac{\sin ^{2} A}{1-\cos A}\).

(v) L.H.S. = \(\frac{\cos A-\sin A+1}{\cos A+\sin A-1}\) using the identity cosec² A

= cosec A + cot A
= R.H.S
∴ L.H.S. = R.H.S.
Hence, \(\frac{\cos A-\sin A+1}{\cos A+\sin A-1}\) using the identity cosec² A = 1 + cot² A.

(vi) L.H.S. = \(\sqrt{\frac{1+\sin A}{1-\sin A}}\)

= \(\sqrt{\frac{(1+\sin A)(1+\sin A)}{(1-\sin A)(1+\sin A)}}\)

= \(\sqrt{\frac{(1+\sin A)^{2}}{(1)^{2}-(\sin A)^{2}}}\)

= \(\sqrt{\frac{(1+\sin A)^{2}}{1-\sin ^{2} A}}=\sqrt{\frac{(1+\sin A)^{2}}{\cos ^{2} A}}\)

= \(\frac{1+\sin A}{\cos A}=\frac{1}{\cos A}+\frac{\sin A}{\cos A}\)
= sec A + tan A
∴ L.H.S. = R.H.S.
Hence, \(\sqrt{\frac{1+\sin A}{1-\sin A}}\) = sec A + tan A.

(vii) L.H.S. = \(\frac{\sin \theta-2 \sin ^{3} \theta}{2 \cos ^{3} \theta-\cos \theta}\)

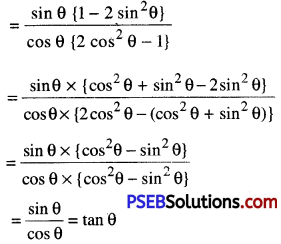
∴ L.H.S. = R.H.S.
Hence, \(\frac{\sin \theta-2 \sin ^{3} \theta}{2 \cos ^{3} \theta-\cos \theta}\) = tan θ

(viii) L.H.S. = (sin A + cosec A)² + (cos A + sec A)²
= (sin² A + cosec² A + 2 sin A × cosec A) + {cos² A + sec² A
+ 2 cos A × sec A)
= [sin² A + co² A + 2sin A × \(\frac{1}{\sin A}\)] + [cos² A + sec² A + 2 cosA × \(\frac{1}{\cos A}\)]
= (sin² A + cosec² A + 2) + (cos² A + sec² A + 2)
= 2 + 2 + (sin² A + cos² A) + sec² A + cosec² A
= 2 + 2 + 1 + 1 + tan² A + 1 + cot² A
= 7 tan² A + cot² A
∴ L.H.S. = R.H.S.
Hence, (sin A + cosec A)² + (cos A + sec A)² = 7 + tan² A + cot² A.

(ix) L.H.S. = (cosec A – sin A) (sec A – cos A)

From (1) and (2), it is clear that
L.H.S. = R.H.S.
Hence, (cosec A – sin A) (sec A – cos A) = \(\frac{1}{\tan A+\cot A}\)

(x) \(\left(\frac{1+\tan ^{2} A}{1+\cot A^{2}}\right)\)
(∵ 1 + tan² A = sec² A
and 1 + cot² A = cosec² A)

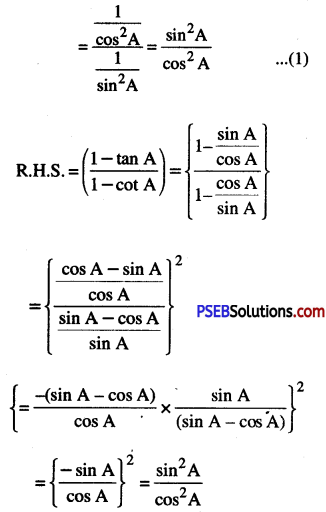
From (1) and (2), it is clear that
LH.S. = R.H.S.
Hence, \(\left(\frac{1+\tan ^{2} A}{1+\cot A^{2}}\right)=\left(\frac{1-\tan A}{1-\cot A}\right)^{2}\) = tan² A.