PSEB 10th Class Maths Solutions Chapter 8 त्रिकोणमिति का परिचय Ex 8.4

by

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 8 त्रिकोणमिति का परिचय Ex 8.4 Textbook Exercise Questions and Answers

PSEB Solutions for Class 10 Maths Chapter 8 त्रिकोणमिति का परिचय Ex 8.4

प्रश्न 1.
त्रिकोणमितीय अनुपातों sin A, sec A और tan A को cot A के पदों में व्यक्त कीजिए।
हल :
सर्वसमिका का प्रयोग करने पर, cosec2 A – cot2 A = 1
⇒ cosec2 A = 1 + cot2 A
⇒ (cosec A)2 = cot2 A + 1
⇒ (\(\left(\frac{1}{\sin A}\right)^{2}\)) = cot2 A + 1
⇒ (sin A)2 = \(\frac{1}{\cot ^{2} A+1}\)
sin A = ± \(\frac{1}{\sqrt{\cot ^{2} A+1}}\)
हम न्यून कोण A के लिए sin A के ऋणात्मक मानों को छोड़ देते हैं।
अतः, sin A = \(\frac{1}{\sqrt{\cot ^{2} A+1}}\)
सर्वसमिका का प्रयोग करने पर,
sec2 A – tan2 A = 1
⇒ sec2 A = 1 + tan2 A
= 1 + \(\frac{1}{\cot ^{2} \mathrm{~A}}\)

= \(\frac{\cot ^{2} \mathrm{~A}+1}{\cot ^{2} \mathrm{~A}}\)

sec A = \(\frac{\sqrt{\cot ^{2} A+1}}{\cot A}\)

tan A = \(\frac{1}{\cot \mathbf{A}}\)

PSEB 10th Class Maths Solutions Chapter 8 त्रिकोणमिति का परिचय Ex 8.4

प्रश्न 2.
∠A के सभी त्रिकोणमितिय अनुपतों को sec A के पदों में लिखिए।
हल :
sin2 A + cos2 A = 1
sin2 A = 1 – cos2 A

= 1 – \(\frac{1}{\sec ^{2} A}\)

= \(\frac{\sec ^{2} \mathrm{~A}-1}{\sec ^{2} \mathrm{~A}}\)

(sin A)2 = \(\frac{\sec ^{2} \mathrm{~A}-1}{\sec ^{2} \mathrm{~A}}\)

sin A = ± \(\sqrt{\frac{\sec ^{2} \mathbf{A}-1}{\sec ^{2} \mathbf{A}}}\)

[न्यून कोण A के लिए – ve चिन्ह को छोड़ दीजिए।]

sin A = \(\sqrt{\frac{\sec ^{2} \mathbf{A}-1}{\sec ^{2} \mathbf{A}}}\)
cos A = \(\frac{1}{\sec A}\)

1 + tan2 A = sec2 A
tan2 A = sec2 A – 1
(tan A)2 = sec2 A – 1
tan A = ± \(\sqrt{\sec ^{2} A-1}\)
[न्यून कोण A के लिए – ve चिन्ह को छोड़ दीजिए।]
अर्थात
tan A = \(\sqrt{\sec ^{2} A-1}\)
cosec A = \(\frac{1}{\sin \mathrm{A}}=\frac{1}{\frac{\sqrt{\sec ^{2} \mathrm{~A}-1}}{\sec \mathrm{A}}}\)

= \(\frac{\sec \mathrm{A}}{\sqrt{\sec ^{2} \mathrm{~A}-1}}\)

cos A = \(\frac{1}{\tan A}=\frac{1}{\sqrt{\sec ^{2} A-1}}\)

PSEB 10th Class Maths Solutions Chapter 8 त्रिकोणमिति का परिचय Ex 8.4

प्रश्न 3.
मान ज्ञात लिका लिए:
(i) \(\frac{\sin ^{2} 63^{\circ}+\sin ^{2} 27^{\circ}}{\cos ^{2} 17^{\circ}+\cos ^{2} 73^{\circ}}\)
(ii) sin 25° cos 65° + cos 25° sin 65°.
हल :
(i) PSEB 10th Class Maths Solutions Chapter 8 त्रिकोणमिति का परिचय Ex 8.4 1

(ii) sin 25° cos 65° + cos 25° sin 65°
= sin 25° × cos (90° – 25°) + cos 25° × sin (90° – 25°)
∵ [cos (90° – θ) = sin θ
sin (90° – θ) = cos θ]
= sin 25° × sin 25° + cos 25° × cos 25°
= sin2 25° + cos2 25°
= 1.

PSEB 10th Class Maths Solutions Chapter 8 त्रिकोणमिति का परिचय Ex 8.4

प्रश्न 4.
सही विकल्प चुनिए और अपने विकल्प की पुष्टि कीजिरा:
(i) 9 sec2 A – 9 tan2 बराबर:
(A) 1
(B) 9
(C) 8
(D) 0.

(ii) (1 + tan θ + sec θ) (1 + cot θ – cosec θ) =
(A) 0
(B) 1
(C) 2
(D) – 1.

(iii) (sec A + tan A) (1 – sin A) बराबर:
(A) sec A
(B) sin A
(C) cosec A
(D) cos A.

(iv) \(\frac{1+\tan ^{2} A}{1+\cot ^{2} A}\) कीजिरा:
(A) sec2 A
(B) – 1
(C) cot2 A.
(D) tan2 A.
हल :
(i) 9 sec2 A – 9 tan2 A
= 9 (sec2 A – tan2 A)
= 9 × 1 = 9.
∴ सही विकल्प (B) है।

(ii) (1 + tan θ + sec θ) (1 + cot θ – cosec θ)

PSEB 10th Class Maths Solutions Chapter 8 त्रिकोणमिति का परिचय Ex 8.4 2

∴ सही विकल्प (B) है।

PSEB 10th Class Maths Solutions Chapter 8 त्रिकोणमिति का परिचय Ex 8.4

(iii) (sec A + tan A) (1 – sin A)
= \(\left(\frac{1}{\cos A}+\frac{\sin A}{\cos A}\right)\) × (1 – sin A)

= \(\frac{(1+\sin A)}{\cos A}\)× (1 – sin A)

= \(\frac{(1+\sin A)(1-\sin A)}{\cos A}\)

= \(\frac{(1)^{2}-(\sin \mathrm{A})^{2}}{\cos \mathrm{A}}=\frac{1-\sin ^{2} \mathrm{~A}}{\cos \mathrm{A}}=\frac{\cos ^{2} \mathrm{~A}}{\cos \mathrm{A}}\)

[∵ cos2 A = 1 – sin2 A]

∴ सही विकल्प (D) है।

(iv) \(\frac{1+\tan ^{2} \mathrm{~A}}{1+\cot ^{2} \mathrm{~A}}\)

PSEB 10th Class Maths Solutions Chapter 8 त्रिकोणमिति का परिचय Ex 8.4 3

∴ सही विकल्प (D) है।

PSEB 10th Class Maths Solutions Chapter 8 त्रिकोणमिति का परिचय Ex 8.4

प्रश्न 5.
निम्नलिखित सर्वसमिकाएँ सिद्ध कीजिए जहाँ वे कोण, जिनके लिए व्यंजक परिभाषित है, न्यून कोण है।
(i) (cosec θ – cot θ)2 = \(\frac{1-\cos \theta}{1+\cos \theta}\)

(ii) \(\frac{\cos \mathbf{A}}{1+\sin \mathbf{A}}+\frac{1+\sin \mathbf{A}}{\cos \mathbf{A}}\) = 2 sec A

(iii) \(\frac{\tan \theta}{1-\cot \theta}+\frac{\cot \theta}{1-\tan \theta}\) = 1 + sec θ cosec θ
[संकेत : व्यंजकों को sin θ और cos θ के पदों में लिखिए।

(iv) \(\frac{1+\sec A}{\sec A}=\frac{\sin ^{2} A}{1-\cos A}\)
[संकेत : L.H.S. और R.H.S. को अलग-अलग सरल कीजिए।]

(v) \(\frac{\cos A-\sin A+1}{\cos A+\sin A-1}\) = cosec A + cot A, सर्वसमिका cosec2 A = 1 + cot2 A को लागू करके

(vi) \(\sqrt{\frac{1+\sin A}{1-\sin A}}\) = sec A + tan A

(vii) \(\frac{\sin \theta-2 \sin ^{3} \theta}{2 \cos ^{3} \theta-\cos \theta}\) = tan θ

(viii) (sin A + cosec A)2 + (cos A + sec A) = 7 + tan2 A + cot2 A

(ix) (cosec A – sin A) (sec A – cos A) = \(\frac{1}{\tan A+\cot A}\)
[संकेत : L.H.S. और R.H.S. को अलग-अलग सरल कीजिए।]

(x) \(\left(\frac{1+\tan ^{2} A}{1+\cot ^{2} A}\right)=\left(\frac{1-\tan A}{1-\cot A}\right)^{2}\)

PSEB 10th Class Maths Solutions Chapter 8 त्रिकोणमिति का परिचय Ex 8.4
हल :
(i) L.H.S. = (cosec θ – cot θ)2

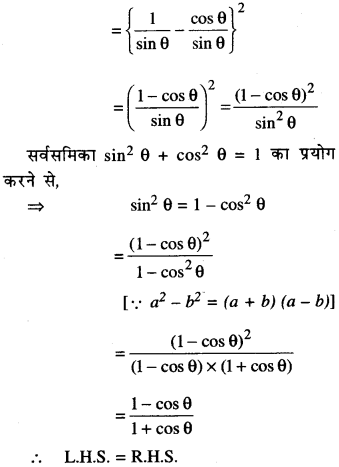
PSEB 10th Class Maths Solutions Chapter 8 त्रिकोणमिति का परिचय Ex 8.4 4

(ii) L.H.S. = \(\frac{\cos A}{1+\sin A}+\frac{1+\sin A}{\cos A}\)

PSEB 10th Class Maths Solutions Chapter 8 त्रिकोणमिति का परिचय Ex 8.4 5

∴ L.H.S = R.H.S

PSEB 10th Class Maths Solutions Chapter 8 त्रिकोणमिति का परिचय Ex 8.4

(iii) L.H.S. = \(\frac{\tan \theta}{1-\cot \theta}+\frac{\cot \theta}{1-\tan \theta}\)

PSEB 10th Class Maths Solutions Chapter 8 त्रिकोणमिति का परिचय Ex 8.4 6

∴ L.H.S = R.H.S

(iv) L.H.S. = \(\frac{1+\sec \mathrm{A}}{\sec \mathrm{A}}=\frac{1+\frac{1}{\cos \mathrm{A}}}{\frac{1}{\cos \mathrm{A}}}\)
= 1 + cos A
R.H.S = \(\frac{\sin ^{2} A}{1-\cos A}\)

= \(\frac{1-\cos ^{2} \mathrm{~A}}{1-\cos \mathrm{A}}\)

= \(\frac{(1+\cos A)(1-\cos A)}{(1-\cos A)}\)

= 1 + cos A

PSEB 10th Class Maths Solutions Chapter 8 त्रिकोणमिति का परिचय Ex 8.4

(v) \(\frac{\cos A-\sin A+1}{\cos A+\sin A-1}\)
(अंश और हर को sin A से विभाजित करने पर

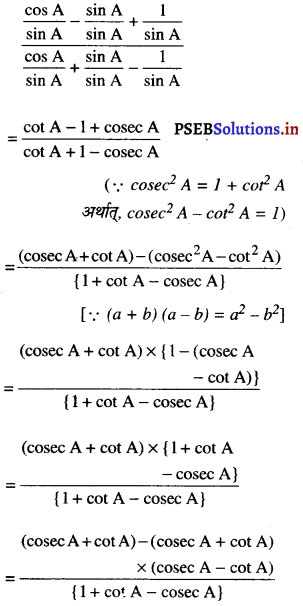
PSEB 10th Class Maths Solutions Chapter 8 त्रिकोणमिति का परिचय Ex 8.4 7

= cosec A + cos A
= R.H.S

PSEB 10th Class Maths Solutions Chapter 8 त्रिकोणमिति का परिचय Ex 8.4

(vi) LH.S = \(\sqrt{\frac{1+\sin \mathrm{A}}{1-\sin \mathrm{A}}}\)

= \(\sqrt{\frac{(1+\sin A)(1+\sin A)}{(1-\sin A)(1+\sin A)}}\)

= \(\sqrt{\frac{(1+\sin A)^{2}}{(1)^{2}-(\sin A)^{2}}}\)

= \(\sqrt{\frac{(1+\sin A)^{2}}{1-\sin ^{2} A}}=\sqrt{\frac{(1+\sin A)^{2}}{\cos ^{2} A}}\)

= \(\frac{1+\sin \mathrm{A}}{\cos \mathrm{A}}=\frac{1}{\cos \mathrm{A}}+\frac{\sin \mathrm{A}}{\cos \mathrm{A}}\)

= sec A + tan A

(vii) L.H.S = \(\frac{\sin \theta-2 \sin ^{3} \theta}{2 \cos ^{3} \theta-\cos \theta}\)

PSEB 10th Class Maths Solutions Chapter 8 त्रिकोणमिति का परिचय Ex 8.4 8

∴ L.H.S = R.H.S

PSEB 10th Class Maths Solutions Chapter 8 त्रिकोणमिति का परिचय Ex 8.4

(viii) L.H.S = (sin A + cosec A)2 + (cos A + sec A)2
= {sin2 A + cosec2 A + 2 sin A × cosec A} + {cos2 A + sec2 A + 2 cos A × sec A}
[∵ cosec A = \(\frac{1}{\sin A}\)]
= [sin2 A + cosec2 A + 2 sin A ×\(\frac{1}{\sin A}\)] + [cos2 A + sec2 A + 2 cos A × \(\frac{1}{\cos A}\)]
= {sin2 A + cosec2 A + 2} + {cos2 A + sec2 A + 2}
[∵ sec A = \(\frac{1}{\cos A}\)]
= 2 + 2 + (sin2 A + cos2 A) + sec2 A + cosec2 A
= 2 + 2 + 1 + 1 + tan2 A + 1 + cot2 A
[∵ sec2 A = tan2 A + 1, cosec2 A = cot2 A + 1]
= 7 tan2 A + cot2 A
∴ L.H.S. = R.H.S.

(ix) L.H.S. = (cosec A – sin A) (sec A – cos A)

PSEB 10th Class Maths Solutions Chapter 8 त्रिकोणमिति का परिचय Ex 8.4 9

= \(\frac{\sin A \cos A}{\sin ^{2} A+\cos ^{2} A}=\frac{\sin A \cos A}{1}\)
∴ L.H.S. = R.H.S.

PSEB 10th Class Maths Solutions Chapter 8 त्रिकोणमिति का परिचय Ex 8.4

(x) L.H.S = \(\left(\frac{1+\tan ^{2} A}{1+\cot ^{2} A}\right)=\frac{\sec ^{2} A}{\ {cosec}^{2} A}\)

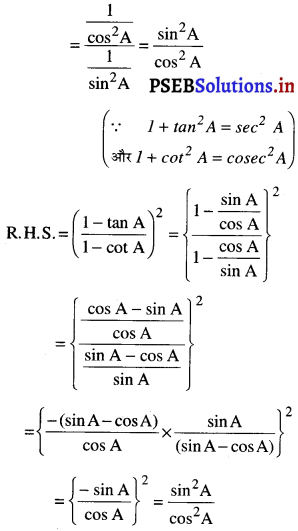
PSEB 10th Class Maths Solutions Chapter 8 त्रिकोणमिति का परिचय Ex 8.4 10

∴ L.H.S. = R.H.S.

Leave a Comment