PSEB 10th Class Maths Solutions Chapter 8 ਤਿਕੋਣਮਿਤੀ ਬਾਰੇ ਜਾਣ ਪਛਾਣ Ex 8.4

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 8 ਤਿਕੋਣਮਿਤੀ ਬਾਰੇ ਜਾਣ ਪਛਾਣ Ex 8.4 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 10 Maths Chapter 8 ਤਿਕੋਣਮਿਤੀ ਬਾਰੇ ਜਾਣ ਪਛਾਣ Exercise 8.4

ਪ੍ਰਸ਼ਨ 1.
ਤਿਕੋਣਮਿਤਈ ਅਨੁਪਾਤਾਂ sin A, sec A ਅਤੇ tan A ਨੂੰ cot A ਦੇ ਪਦਾਂ ਵਿਚ ਦਰਸਾਉ।
ਹੱਲ:
ਤਤਸਮਕ ਦਾ ਪ੍ਰਯੋਗ ਕਰਨ ‘ਤੇ,
cosec² A – cot² A = 1
⇒ cosec² A = 1 + cot² A
⇒ (cosec A)² = cot² A + 1
⇒ \(\left(\frac{1}{\sin A}\right)^{2}\) = cot² A + 1
⇒ (sin A)² = \(\frac{1}{\cot ^{2} \mathrm{~A}+1}\)
⇒ sin A = ±\(\frac{1}{\sqrt{\cot ^{2} A+1}}\)
ਅਸੀਂ ਨਿਉਨ ਕੋਣ A ਦੇ ਲਈ sin A ਦੇ ਰਿਣਾਤਮਕ ਮੁੱਲ ਛਡ ਦਿੰਦੇ ਹਨ ।
∴ sin A = \(\frac{1}{\sqrt{\cot ^{2} A+1}}\)
ਤਤਸਮਕ ਦਾ ਪ੍ਰਯੋਗ ਕਰਨ ਤੇ,
sec² A – tan² A = 1
⇒ sec² A = 1 + tan² A

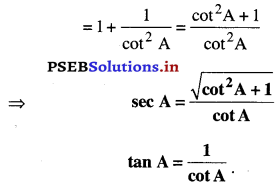
ਪ੍ਰਸ਼ਨ 2.
∠A ਦੇ ਬਾਕੀ ਸਾਰੇ ਤਿਕੋਣਮਿਤਈ ਅਨੁਪਾਤਾਂ ਨੂੰ sec A ਦੇ ਪਦਾਂ ਵਿੱਚ ਦਰਸਾਉ ।
ਹੱਲ:
sin² A + cos² A = 1
⇒ sin² A = 1 – cos² A

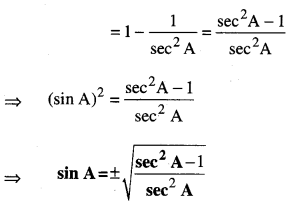
[ਨਿਊਨ ਕੋਣ A ਦੇ ਲਈ – ve ਚਿੰਨ੍ਹ ਨੂੰ ਛੱਡ ਦਿਓ]
⇒ sin A = \(\frac{\sqrt{\sec ^{2} A-1}}{\sec A}\)
cos A = \(\frac{1}{\sec A}\)
1 + tan² A = sec² A
tan² A = sec² A – 1
(tan A)² = sec² A – 1
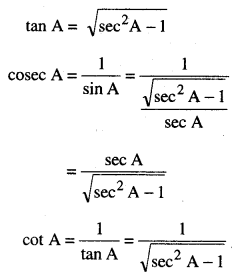
⇒ tan A = ±\(\sqrt{\sec ^{2} A-1}\)
[ਨਿਊਨ ਕੋਣ A ਦੇ ਲਈ – ve ਚਿੰਨ੍ਹ ਨੂੰ ਛੱਡ ਦਿਓ]

3. ਮੁੱਲ ਪਤਾ ਕਰੇ :

ਪ੍ਰਸ਼ਨ (i).
\(\frac{\sin ^{2} 63^{\circ}+\sin ^{2} 27^{\circ}}{\cos ^{2} 17^{\circ}+\cos ^{2} 73^{\circ}}\)
ਉੱਤਰ:

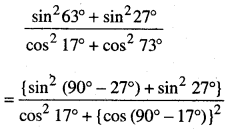
∵ sin (90° – θ)= cos θ
ਅਤੇ cos (90° – θ) = sin θ.
= \(\frac{\cos ^{2} 27^{\circ}+\sin ^{2} 27^{\circ}}{\cos ^{2} 17^{\circ}+\sin ^{2} 17^{\circ}}\)
= \(\frac{1}{1}\) = 1

ਪ੍ਰਸ਼ਨ (ii).
sin 25° cos 65° + cos 25° sin 65°.
ਉੱਤਰ:
sin 25° cos 65° + cos 25° sin 65°
= sin 25° × cos (90° – 25°) + cos 25° × sin (90° – 25°)
∵ cos (90° – θ) = sin θ
sin (90° – θ) = cos θ
= sin 25° × sin 25° + cos 25° × cos 25°
= sin² 25° + cos² 25°
= 1.

4. ਸਹੀ ਉੱਤਰ ਚੁਣੋ ਅਤੇ ਆਪਣੇ ਵਿਕਲਪ ਦੀ ਪੁਸ਼ਟੀ ਕਰੇ:

ਪ੍ਰਸ਼ਨ (i).
9 sec² A – 9 tan²
(A) 1
(B) 9
(C) 8
(D) 0
ਉੱਤਰ:
9 sec² A – 9 tan² A
= 9 (sec² A – tan² A)
= 9 × 1 = 9.
∴ ਸਹੀ ਵਿਕਲਪ (B) ਹੈ

ਪ੍ਰਸ਼ਨ (ii).
(1 + tan θ + sec θ) (1 + cotθ – cosec θ) ਬਰਾਬਰ ਹੈ :
(A) 0
(B) 1
(C) 2
(D) -1.
ਉੱਤਰ:
(1 + tan θ + sec θ) (1 + cotθ – cosec θ)


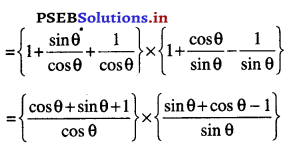
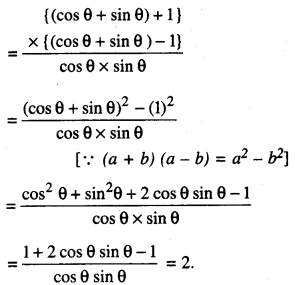
∴ ਸਹੀ ਵਿਕਲਪ (C) ਹੈ

ਪ੍ਰਸ਼ਨ (iii).
(sec A + tan A) (1 – sin A) ਬਰਾਬਰ ਹੈ :
(A) sec A
(B) sin A
(C) cosec A
(D) cos A.
ਉੱਤਰ:
(sec A + tan A) (1 – sin A)

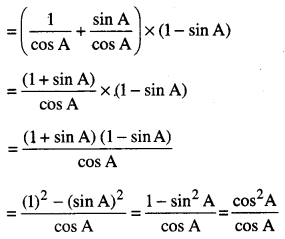
[∵ cos² A = 1 – sin² A]
= cos A.
∴ ਸਹੀ ਵਿਕਲਪ (D) ਹੈ

ਪ੍ਰਸ਼ਨ (iv).
\(\frac{1+\tan ^{2} A}{1+\cot ^{2} A}\)
(A) sec² A
(B) -1
(C) cot² A
(D) tan² A.
ਉੱਤਰ:
\(\frac{1+\tan ^{2} A}{1+\cot ^{2} A}\)

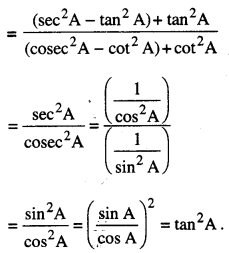
∴ ਸਹੀ ਵਿਕਲਪ (D) ਹੈ

5. ਹੇਠਾਂ ਦਿੱਤੀਆਂ ਸਰਬਸਮਤਾਵਾਂ (ਤਤਸਮਕਾਂ) ਸਿੱਧ ਕਰੋ, ਜਿੱਥੇ ਉਹ ਕੋਣ ਜਿਨ੍ਹਾਂ ਲਈ ਵਿਅੰਜਕਾਂ ਪਰਿਭਾਸ਼ਿਤ ਹਨ, ਨਿਊਨ ਕੋਣ ਹਨ :

ਪ੍ਰਸ਼ਨ (i).
(cosec θ – cot θ)² = \(\frac{1-\cos \theta}{1+\cos \theta}\)
ਉੱਤਰ:
L.H.S. = (cosec θ – cot θ)²
= \(\left\{\frac{1}{\sin \theta}-\frac{\cos \theta}{\sin \theta}\right\}^{2}\)

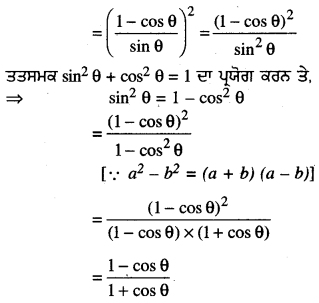
∴ L.H.S. = R.H.S.

ਪ੍ਰਸ਼ਨ (ii).
\(\frac{\cos A}{1+\sin A}\) + \(\frac{1+\sin A}{\cos A}\) = 2 sec A
ਉੱਤਰ:
L.H.S. = \(\frac{\cos A}{1+\sin A}\) + \(\frac{1+\sin A}{\cos A}\)

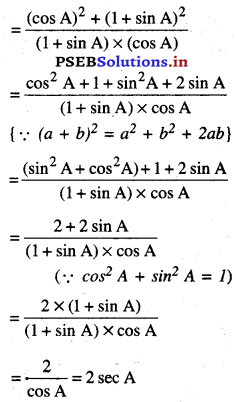
∴ L.H.S. = R.H.S.

ਪ੍ਰਸ਼ਨ (iii).
\(\frac{\tan \theta}{1-\cot \theta}\) + \(\frac{\cot \theta}{1-\tan \theta}\) = 1 + secθcosecθ
[ਸੰਕੇਤ : ਵਿਅੰਜਕ ਨੂੰ sin θ, ਅਤੇ cos θ ਦੇ ਪਦਾਂ ਵਿੱਚ ਲਿਖੋ1]
ਉੱਤਰ:
L.H.S. = \(\frac{\tan \theta}{1-\cot \theta}\) + \(\frac{\cot \theta}{1-\tan \theta}\)



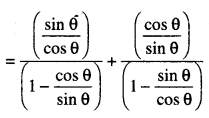
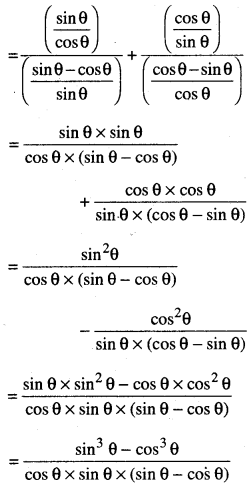
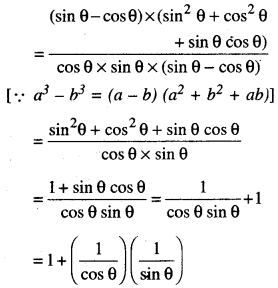
= 1 + sec θ cosec θ
∴ L.H.S. = R.H.S.

ਪ੍ਰਸ਼ਨ (iv).
\(\frac{1+\sec A}{\sec A}\) = \(\frac{\sin ^{2} A}{1-\cos A}\)
[ਸੰਕੇਤ : ਖੱਬੇ ਪਾਸੇ ਅਤੇ ਸੱਜੇ ਪਾਸੇ ਨੂੰ ਅਲੱਗ-ਅਲੱਗ ਸਰਲ ਕਰੋ ]
ਉੱਤਰ:


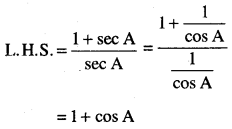
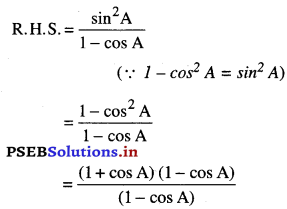
= 1 + cos A.
∴ L.H.S. = R.H.S.

ਪ੍ਰਸ਼ਨ (v).
ਤਤਮਸਕ cosec² A = 1 + cot² A ਨੂੰ ਵਰਤਦੇ ਹੋਏ, ਸਿੱਧ ਕਰੋ :
\(\frac{\cos A-\sin A+1}{\cos A+\sin A-1}\) = cosec A + cot A,
ਉੱਤਰ:
\(\frac{\cos A-\sin A+1}{\cos A+\sin A-1}\)
(ਅੰਸ਼ ਅਤੇ ਹਰ ਨੂੰ sin A ਨਾਲ ਭਾਗ ਕਰਨ ਤੇ)

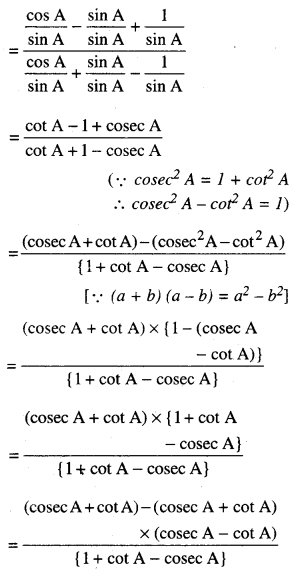
= cosec A + cot A
= R.H.S.

ਪ੍ਰਸ਼ਨ (vi).
\(\sqrt{\frac{1+\sin A}{1-\sin A}}\) = sec A + tan A
ਉੱਤਰ:
L.H.S. = \(\sqrt{\frac{1+\sin A}{1-\sin A}}\)

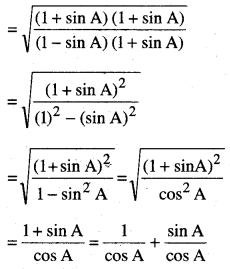
= sec A + tan A
∴ L.H.S. = R.H.S.

ਪ੍ਰਸ਼ਨ (vii).
\(\frac{\sin \theta-2 \sin ^{3} \theta}{2 \cos ^{3} \theta-\cos \theta}\) = tan θ
ਉੱਤਰ:
L.H.S. = \(\frac{\sin \theta-2 \sin ^{3} \theta}{2 \cos ^{3} \theta-\cos \theta}\)

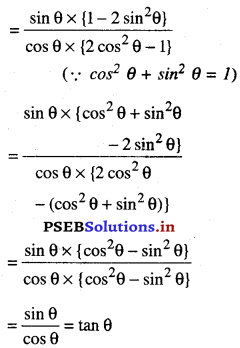
∴ L.H.S. = R.H.S.

ਪ੍ਰਸ਼ਨ (viii).
(sin A + cosec A)² + (cos A + sec A)² = 7 + tan² A + cot² A
ਉੱਤਰ:
L.H.S. = (sin A + cosec A)² + (cos A + sec A)²
= {sin² A + cosec² A + 2 sin A × cosec A} + {cos² A + sec² A + 2 cos A × sec A}
[∵ cosec A = \(\frac{1}{\sin A}\)]

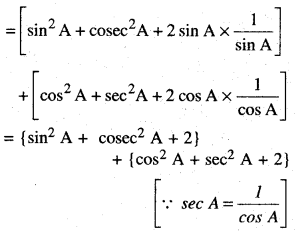
= 2 + 2 + (sin² A + cos² A) + sec² A + cosec² A
= 2 + 2 + 1 + 1 + tan² A + 1 + cot² A
(∵ sec² A = tan² A + 1,
(cosec² A = cot² A + 1)
= 7 + tan² A + cot² A
∴ L.H.S. = R.H.S.

ਪ੍ਰਸ਼ਨ (ix).
(cosec A – sin A) (sec A – cos A) = \(\frac{1}{\tan A+\cot A}\)
[ਸੰਕੇਤ : ਖੱਬੇ ਪਾਸੇ ਅਤੇ ਸੱਜੇ ਪਾਸੇ ਨੂੰ ਅਲੱਗ-ਅਲੱਗ ਸਰਲ ਕਰੋ]
ਉੱਤਰ:
L.H.S. = (cosec A – sin A) (sec A – cos A)

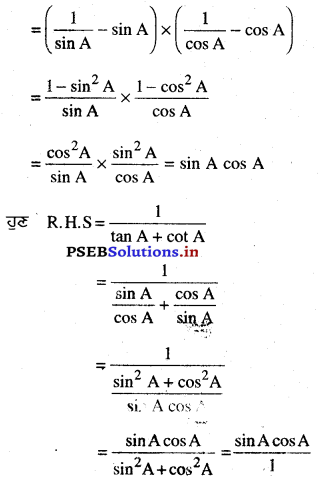
∴ L.H.S. = R.H.S.

ਪ੍ਰਸ਼ਨ (x).
\(\left(\frac{1+\tan ^{2} A}{1+\cot ^{2} A}\right)\) = \(\left(\frac{1-\tan A}{1-\cot A}\right)^{2}\) = tan² A
ਉੱਤਰ:

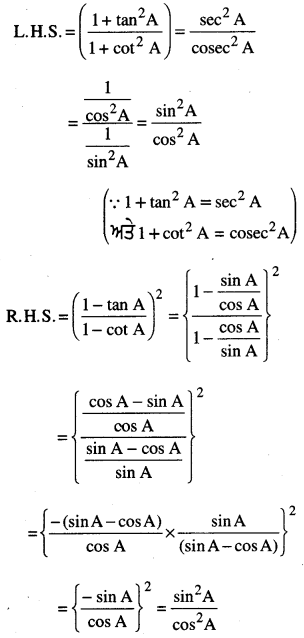
∴ L.H.S. = R.H.S.