PSEB 10th Class Maths Solutions Chapter 9 ਤਿਕੋਣਮਿਤੀਦੇ ਕੁਝ ਉਪਯੋਗ Ex 9.1

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 9 ਤਿਕੋਣਮਿਤੀਦੇ ਕੁਝ ਉਪਯੋਗ Ex 9.1 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 10 Maths Chapter 9 ਤਿਕੋਣਮਿਤੀਦੇ ਕੁਝ ਉਪਯੋਗ Exercise 9.1

ਪ੍ਰਸ਼ਨ 1.
ਸਰਕਸ ਦਾ ਇੱਕ ਕਲਾਕਾਰ ਇੱਕ 20 m ਲੰਬੀ ਰੱਸੀ ‘ਤੇ ਚੜ੍ਹ ਰਿਹਾ ਹੈ ਜੋ ਪੂਰੀ ਤਰ੍ਹਾਂ ਨਾਲ ਤਣੀ (ਕਸੀ) ਹੋਈ ਹੈ ਅਤੇ ਧਰਤੀ ‘ਤੇ ਸਿੱਧੇ ਖੜੇ ਖੰਬੇ ਦੇ ਸਿਖਰ ਨਾਲ ਬੰਨੀ ਹੋਈ ਹੈ। ਜੇਕਰ ਰੱਸੀ ਧਰਤੀ ਦੇ ਤਲ ਨਾਲ 30° ਦਾ ਕੋਣ ਬਣਾਉਂਦੀ ਹੋਵੇ ਤਾਂ ਖੰਬੇ ਦੀ ਉੱਚਾਈ ਪਤਾ ਕਰੋ ।(ਦੇਖੋ ਚਿੱਤਰ)।

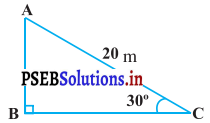
ਹੱਲ:
ਮੰਨ ਲਉ AB ਖੰਬੇ ਦੀ ਉੱਚਾਈ ਹੈ।
AC = 20 m ਰੱਸੀ ਦੀ ਲੰਬਾਈ

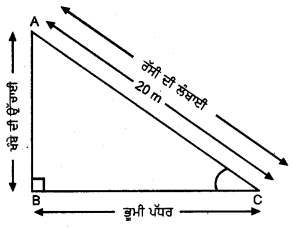
ਇਸ ਸਥਿਤੀ ਵਿਚ ਉਚਾਣ ਕੋਣ 30° ਹੈ ।
ਸਮਕੋਣ △ABC ਵਿੱਚ,
ਜਾਂ \(\frac{AB}{AC}\) = sin 30°
ਜਾਂ AB = \(\frac{1}{2}\) × 20 = 10
∴ ਖੰਬੇ ਦੀ ਉਚਾਈ 10 m ਹੈ ।

ਪ੍ਰਸ਼ਨ 2.
ਹਨੇਰੀ ਆਉਣ ਨਾਲ ਇੱਕ ਦਰੱਖਤ ਟੁੱਟ ਜਾਂਦਾ ਹੈ ਅਤੇ ਟੁੱਟਿਆ ਹੋਇਆ ਭਾਗ ਇਸ ਤਰ੍ਹਾਂ ਨਾਲ ਮੁੜ ਜਾਂਦਾ ਹੈ ਕਿ ਦਰੱਖਤ ਦਾ ਸਿਖ਼ਰ ਜਮੀਨ ਨੂੰ ਛੂਹਣ (touch) ਲੱਗਦਾ ਹੈ ਹੈ ਅਤੇ ਇਸ ਦੇ ਨਾਲ 30° ਦਾ ਕੋਣ ਬਣਾਉਂਦਾ ਹੈ । ਦਰੱਖ਼ਤ ਦੇ ਆਧਾਰ ਬਿੰਦੂ ਦੀ ਦੂਰੀ, ਜਿੱਥੇ ਦਰੱਖ਼ਤ ਦਾ ਸਿਖਰ ਜਮੀਨ ਨੂੰ ਛੂਹਦਾ ਹੈ, 8 m ਹੈ । ਦਰਖ਼ਤ ਦੀ ਉੱਚਾਈ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਮੰਨ ਲਉ ਹਨੇਰੀ ਤੋਂ ਪਹਿਲਾਂ ਦਰੱਖ਼ਤ ਦੀ ਉੱਚਾਈ BD ਹੈ । ਹਨੇਰੀ ਤੋਂ ਬਾਅਦ AD = AC = ਟੁੱਟੇ ਹੋਏ ਦਰੱਖ਼ਤ ਦੇ ਦੋ ਭਾਗਾਂ ਦੀ ਲੰਬਾਈ (ਚਿੱਤਰ ਵਿਚ ਦਿਖਾਏ ਤੋਂ ਅਨੁਸਾਰ

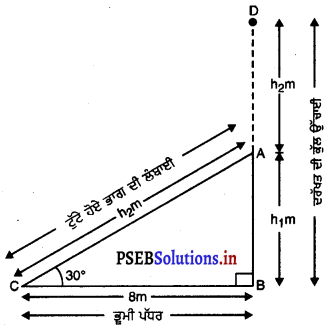
ਸਮਕੋਣ △ABC ਵਿੱਚ,
\(\frac{AB}{BC}\) = tan 30°

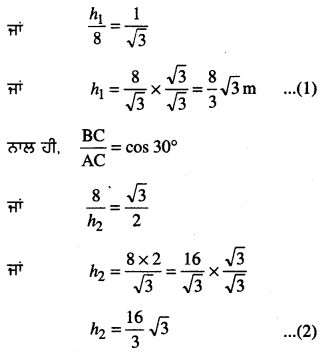
ਦਰੱਖਤ ਦੀ ਕੁੱਲ ਉੱਚਾਈ = h₁ + h₂
= \(\frac{8}{3}\)\(\sqrt {3}\) + \(\frac{16}{3}\)\(\sqrt {3}\) [(1) ਅਤੇ (2) ਤੋਂ।]
= [latex]\frac{8+16}{3}[/latex]\(\sqrt {3}\) = \(\frac{24}{3}\)\(\sqrt {3}\)
= 8\(\sqrt {3}\) m
∴ ਦਰੱਖ਼ਤ ਦੀ ਉੱਚਾਈ 83 m ਹੈ ।

ਪ੍ਰਸ਼ਨ 3.
ਇਕ ਠੇਕੇਦਾਰ ਬੱਚਿਆਂ ਦੇ ਖੇਡਣ ਵਾਲੇ ਇਕ ਪਾਰਕ ਵਿਚ ਦੋ ਤਿਲਕਣ ਪੱਟੀਆਂ (Slides) ਨੂੰ ਲਗਾਉਣਾ ਚਾਹੁੰਦਾ ਹੈ । 5 ਸਾਲ ਤੋਂ ਘੱਟ ਉਮਰ ਦੇ ਬੱਚਿਆਂ ਲਈ ਉਹ ਇਸ ਤਰਾਂ ਦੀ ਤਿਲਕਣ ਪੱਟੀ ਲਗਾਉਣਾ ਚਾਹੁੰਦਾ ਹੈ ਜਿਸ ਦਾ ਸਿਖਰ 1.5 m ਉੱਚਾਈ ‘ਤੇ ਹੋਵੇ ਅਤੇ ਉਹ ਜਮੀਨ ਨਾਲ 30° ਕੋਣ ‘ ਤੇ ਝੁਕੀ ਹੋਵੇ, ਜਦੋਂ ਕਿ ਇਸ ਤੋਂ ਵੱਧ ਉਮਰ ਦੇ ਬੱਚਿਆਂ ਲਈ ਉਹ 3m ਦੀ ਉੱਚਾਈ ‘ਤੇ ਇੱਕ ਵੱਧ ਢਾਲ ਦੀ ਤਿਲਕਣਪੱਟੀ ਲਗਾਉਣਾ ਚਾਹੁੰਦਾ ਹੈ ਜੋ ਜਮੀਨ ਨਾਲ 60° ਦਾ ਕੋਣ ਬਣਾਉਂਦੀ ਹੋਵੇ । ਹਰ ਇੱਕ ਸਥਿਤੀ ਵਿੱਚ ਤਿਲਕਣ ਪੱਟੀ ਦੀ ਲੰਬਾਈ ਕਿੰਨੀ ਹੋਣੀ ਚਾਹੀਦੀ ਹੈ।
ਹੱਲ:
ਸਥਿਤੀ 1. 5 ਸਾਲ ਤੋਂ ਛੋਟੇ ਬੱਚਿਆਂ ਲਈ
ਮੰਨ ਲਉ AC = l₁m ਤਿਲਕਣ ਪੱਟੀ ਦੀ ਲੰਬਾਈ ਹੈ ਅਤੇ BC = 1.5 m ਤਿਲਕਣ ਪੱਟੀ ਦੀ ਉੱਚਾਈ ਹੈ । ਇਸ ਸਥਿਤੀ ਵਿਚ ਜ਼ਮੀਨ ਨਾਲ ਬਣਿਆ ਕੋਣ 30° ਦਾ ਹੈ (ਦੇਖੋ ਚਿੱਤਰ)

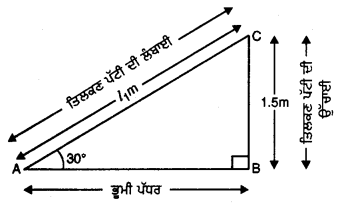
ਸਮਕੋਣ △ABC ਵਿੱਚ,
\(\frac{BC}{AC}\) = sin 30°
ਜਾਂ \(\frac{1 \cdot 5}{l_{1}}\) = \(\frac{1}{2}\)
ਜਾਂ l₁ = 1.5 × 2 = 3m
ਸਥਿਤੀ II. 5 ਸਾਲ ਤੋਂ ਵੱਧ ਉਮਰ ਦੇ ਬੱਚਿਆਂ ਲਈ
ਮੰਨ ਲਉ AC = l₂m ਤਿਲਕਣ ਪੱਟੀ ਦੀ ਲੰਬਾਈ ਹੈ ਅਤੇ BC = 3 m ਤਿਲਕਣ ਪੱਟੀ ਦੀ ਉੱਚਾਈ ਹੈ ਅਤੇ ਜਮੀਨ ਨਾਲ ਬਣਿਆ ਕੋਣ 60° ਦਾ ਹੈ । (ਦੇਖੋ ਚਿੱਤਰ) ।

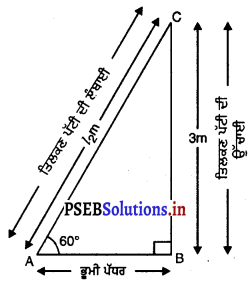
ਸਮਕੋਣ △ABC ਵਿੱਚ
\(\frac{BC}{AC}\) = sin 60°
ਜਾਂ \(\frac{3}{l_{2}}\) = \(\frac{\sqrt{3}}{2}\)
ਜਾਂ l₂ = \(\frac{3 \times 2}{\sqrt{3}}\) = \(\frac{6}{\sqrt{3}}\)
= \(\frac{6}{\sqrt{3}}\) × \(\frac{\sqrt{3}}{\sqrt{3}}\) = \(\frac{6 \sqrt{3}}{3}\) = 2\(\sqrt {3}\) m
∴ 5 ਸਾਲ ਤੋਂ ਛੋਟੇ ਬੱਚਿਆਂ ਲਈ ਅਤੇ ਉਸ ਤੋਂ ਵੱਧ ਉਮਰ ਦੇ ਬੱਚਿਆਂ ਲਈ ਤਿਲਕਣ ਪੱਟੀ ਦੀ ਲੰਬਾਈ ਕੁਮਵਾਰ
3 m ਅਤੇ 2\(\sqrt {3}\)m ਹੈ ।

ਪ੍ਰਸ਼ਨ 4.
ਜਮੀਨ ਦੇ ਇਕ ਬਿੰਦੂ ਤੋਂ ਜੋ ਮੀਨਾਰ ਦੇ ਆਧਾਰ ਬਿੰਦੂ ਤੋਂ 30 m ਦੀ ਦੂਰੀ ‘ਤੇ ਹੈ, ਮੀਨਾਰ ਦੇ ਸਿਖ਼ਰ ਦਾ ਉੱਚਾਣ ਕੋਣ 30° ਹੈ । ਮੀਨਾਰ ਦੀ ਉੱਚਾਈ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਮੰਨ ਲਉ BC = h m ਮੀਨਾਰ ਦੀ ਉੱਚਾਈ ਹੈ ਅਤੇ AB = 30 m ਆਧਾਰ ਤੋਂ ਬਿੰਦੂ ਦੀ ਦੂਰੀ (ਦੇਖੋ ਚਿੱਤਰ) ਹੈ।

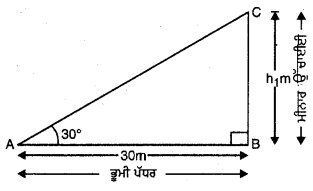
ਸਮਕੋਣ △ABC ਵਿੱਚ,
\(\frac{BC}{AB}\) = tan 30°
ਜਾਂ \(\frac{h}{30}\) = \(\frac{1}{1}\)
ਜਾਂ h = \(\frac{30}{\sqrt{3}}\) × \(\frac{\sqrt{3}}{\sqrt{3}}\) = \(\frac{30 \sqrt{3}}{3}\)
= 10\(\sqrt {3}\) = 10 × 1.732
h = 17:32 m
ਮੀਨਾਰ ਦੀ ਉੱਚਾਈ ਲਗਭਗ 17.32 m. ਹੈ ।

ਪ੍ਰਸ਼ਨ 5.
ਜਮੀਨ ਤੋਂ 60 m ਉੱਚਾਈ ‘ਤੇ ਇੱਕ ਪਤੰਗ ਉੱਡ ਰਹੀ ਹੈ। ਪਤੰਗ ਨਾਲ ਲੱਗੇ ਧਾਗੇ ਨੂੰ ਅਸਥਾਈ ਰੂਪ ਵਿੱਚ ਜਮੀਨ ‘ਤੇ ਇੱਕ ਬਿੰਦੂ ਨਾਲ ਬੰਨ ਦਿੱਤਾ ਗਿਆ ਹੈ। ਜ਼ਮੀਨ ਨਾਲ ਧਾਗੇ ਦਾ ਝੁਕਾਵ 60° ਹੈ। ਇਹ ਮੰਨਕੇ ਕਿ ਧਾਗੇ ਵਿੱਚ ਕੋਈ ਢਿੱਲ ਨਹੀਂ ਹੈ , ਧਾਗੇ ਦੀ ਲੰਬਾਈ ਪਤਾ ਕਰੋ।
ਹੱਲ:
ਮੰਨ ਲਉ ਬਿੰਦੂ ਤੇ ਪਤੰਗ ਦੀ ਸਥਿਤੀ ਹੈ AC = l m ਪਤੰਗ ਦੇ ਨਾਲ ਲੱਗੇ ਧਾਗੇ ਦੀ ਲੰਬਾਈ ਸਿਖਰ ਕੋਣ 60° ਦਾ ਹੈ । (ਦੇਖੋ ਚਿੱਤਰ)

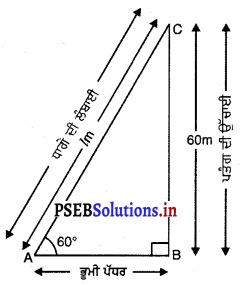
ਸਮਕੋਣ △ABC ਵਿੱਚ,
\(\frac{CB}{CA}\) = sin 60°
ਜਾਂ \(\frac{60}{l}\) = \(\frac{\sqrt{3}}{2}\)
ਜਾਂ l = \(\frac{60 \times 2}{\sqrt{3}}\) = \(\frac{120}{\sqrt{3}}\) × \(\frac{\sqrt{3}}{\sqrt{3}}\)
= \(\frac{120 \sqrt{3}}{3}\) = 40\(\sqrt {3}\) m
∴ ਧਾਗੇ ਦੀ ਲੰਬਾਈ 403 m ਹੈ ।

ਪ੍ਰਸ਼ਨ 6.
1.5 m ਲੰਬਾ ਲੜਕਾ 30 ਮੀਟਰ ਉੱਚੀ ਇੱਕ ਇਮਾਰਤ | ਤੋਂ ਕੁੱਝ ਦੂਰੀ ‘ਤੇ ਖੜ੍ਹਾ ਹੈ । ਜਦੋਂ ਉਹ ਇਮਾਰਤ ਵੱਲ ਜਾਂਦਾ ਹੈ (ਚਲਦਾ ਹੈ। ਤਾਂ ਉਸਦੀ ਅੱਖ ਨਾਲ ਇਮਾਰਤ ਦੇ ਸਿਖ਼ਰ ਦਾ | ਉੱਚਾਣ ਕੋਣ 30° ਤੋਂ 60° ਹੋ ਜਾਂਦਾ ਹੈ । ਦੱਸੋ ਕਿ ਉਹ | ਇਮਾਰਤ ਵੱਲ ਕਿੰਨੀ ਦੂਰੀ ਤੱਕ ਚਲ ਕੇ ਗਿਆ ?
ਹੱਲ:
ਮੰਨ ਲਉ ED = 30 m ਇਮਾਰਤ ਦੀ ਉੱਚਾਈ | ਹੈ ਅਤੇ EC = 1.5 m ਲੜਕੇ ਦੀ ਉੱਚਾਈ ਹੈ । ਭਿੰਨ-ਭਿੰਨ | ਸਥਿਤੀਆਂ ਵਿਚ ਸਿਖ਼ਰ ਦਾ ਉੱਚਾਣ ਕੋਣ 30° ਅਤੇ 60° ਹੈ । (ਦੇਖੋ ਚਿੱਤਰ)

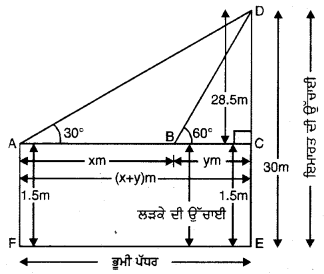
ਸਮਕੋਣ △ACD ਵਿੱਚ,
\(\frac{DC}{AC}\) = tan 30°
ਜਾਂ \(\frac{28.5}{x+y}\) = \(\frac{1}{\sqrt{3}}\)
ਜਾਂ x + y = 28.5 × \(\sqrt {3}\) m …(1)
ਹੁਣ, ਸਮਕੋਣ △BCD ਵਿੱਚ,

∴ ਲੜਕੇ ਦੁਆਰਾ ਇਮਾਰਤ ਵੱਲ ਤੈਅ ਕੀਤੀ ਦੂਰੀ 19\(\sqrt {3}\) m ਹੈ ।

ਪ੍ਰਸ਼ਨ 7.
ਜਮੀਨ ਦੇ ਇੱਕ ਬਿੰਦੂ ਤੋਂ ਇੱਕ 20 m ਉੱਚੀ ਇਮਾਰਤ ਦੇ ਸਿਖ਼ਰ ‘ਤੇ ਲੱਗੇ ਸੰਚਾਰ ਮੀਨਾਰ (transmission tower) ਦੇ ਤਲ ਅਤੇ ਸਿਖ਼ਰ ਦਾ ਉੱਚਾਣ ਕੋਣ ਕੁਮਵਾਰ 45° ਅਤੇ 60° ਹੈ। ਸੰਚਾਰ ਮੀਨਾਰ ਦੀ ਉੱਚਾਈ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਮੰਨ ਲਉ BC = 20 m ਇਮਾਰਤ ਦੀ ਉੱਚਾਈ ਹੈ DC=h m ਸੰਚਾਰ ਮੀਨਾਰ ਦੀ ਉੱਚਾਈ ਹੈ । ਇਮਾਰਤ ਦੇ ਸਿਖਰ ਤੇ ਲੱਗੀ ਇਕ ਸੰਚਾਰ ਮੀਨਾਰ ਦੇ ਤਲ ਅਤੇ ਸਿਖਰ ਦੇ ਉੱਚਾਣ ਕੋਣ ਕੁਮਵਾਰ 45° ਅਤੇ 60° ਹੈ । (ਦੇਖੋ ਚਿੱਤਰ)

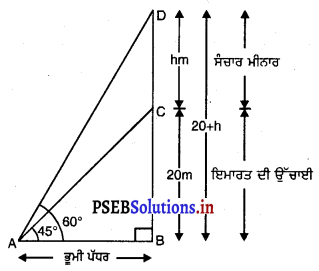
ਸਮਕੋਣ △ABC ਵਿੱਚ,
\(\frac{AB}{BC}\) = cot 45°
ਜਾਂ \(\frac{AB}{20}\) = 1
ਜਾਂ AB = 20 m ….(1)
ਨਾਲ ਹੀ, ਸਮਕੋਣ △ABD ਵਿੱਚ,
\(\frac{AB}{BD}\) = cot 60°
ਜਾਂ \(\frac{AB}{20+h}\) = \(\frac{1}{\sqrt{3}}\)
ਜਾਂ AB = \(\frac{20+h}{\sqrt{3}}\)
ਜਾਂ AB = \(\frac{(20+h)}{\sqrt{3}}\) ….(2)
(1) ਅਤੇ (2) ਤੋਂ ,
20 = \(\frac{(20+h)}{\sqrt{3}}\)
ਜਾਂ 20\(\sqrt {3}\) = 20 + h
ਜਾਂ h = 20\(\sqrt {3}\) – 20
ਜਾਂ h = 20(\(\sqrt {3}\) – 1)m
= 20 (1732 – 1) m
= 20 × 0.732 = 14∙64 m
∴ ਸੰਚਾਰ ਮੀਨਾਰ ਦੀ ਉੱਚਾਈ 1464 m ਹੈ ।

ਪ੍ਰਸ਼ਨ 8.
ਇੱਕ ਪੈਡਸਟਲ (Pedestal) ਦੇ ਸਿਖਰ ‘ਤੇ ਇੱਕ 1.6 m ਉੱਚੀ ਮੂਰਤੀ ਲੱਗੀ ਹੋਈ ਹੈ । ਜਮੀਨ ਦੇ ਇੱਕ ਬਿੰਦੂ ਤੋਂ ਮੂਰਤੀ ਦੇ ਸਿਖ਼ਰ ਦਾ ਉੱਚਾਣ ਕੋਣ 60° ਹੈ ਅਤੇ ਇਸ ਹੀ ਬਿੰਦੂ ਤੋਂ ਪੈਡਸਟਲ ਦੇ ਸਿਖ਼ਰ ਦਾ ਉੱਚਾਣ ਕੋਣ 45° ਹੈ । ਪੈਡਸਟਲ ਦੀ ਉੱਚਾਈ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਮੰਨ ਲਉ BC = hm ਪੈਡਸਟਲ ਦੀ ਉੱਚਾਈ ਹੈ CD = 1.6 m ਮੂਰਤੀ ਦੀ ਉੱਚਾਈ ਹੈ । ਜਮੀਨ ‘ਤੇ ਦਿੱਤੇ ਬਿੰਦੁ A ਤੋਂ ਮੁਰਤੀ ਦੇ ਸਿਖ਼ਰ ਅਤੇ ਪੈਡਸਟਲ ਦੇ ਸਿਖਰ ਦਾ ਉੱਚਾਂਣ ਕੋਣ 60° ਅਤੇ 45° ਹੈ । (ਦੇਖੋ ਚਿੱਤਰ)

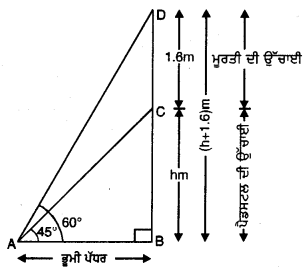
ਸਮਕੋਣ △ABC ਵਿੱਚ,
\(\frac{AB}{BC}\) = cot 45°
ਜਾਂ \(\frac{AB}{h}\) = 1
ਜਾਂ AB = h m …(1)
ਸਮਕੋਣ △ABD ਵਿੱਚ,
\(\frac{AB}{BD}\) = cot 60°
ਜਾਂ \(\frac{AB}{h+1.6}\) = \(\frac{1}{\sqrt{3}}\)
ਜਾਂ AB = \(\frac{h+1.6}{\sqrt{3}}\) ….(2)
(1) ਅਤੇ (2), ਤੋਂ
h = \(\frac{h+1.6}{\sqrt{3}}\)
ਜਾਂ \(\sqrt {3}\)h = h + 1∙6
ਜਾਂ (\(\sqrt {3}\) – 1) h = 1∙6
ਜਾਂ (1∙732 – 1) h = 1∙6
ਜਾਂ (0∙732)h = 1∙6
ਜਾਂ h = \(\frac{1∙6}{0∙732}\) = 2·1857923
= 2·20 m (ਲਗਭਗ)
∴ ਪੈਡਸਟਲ ਦੀ ਉੱਚਾਈ 2:20 m ਹੈ ।

ਪ੍ਰਸ਼ਨ 9.
ਇੱਕ ਮੀਨਾਰ ਦੇ ਆਧਾਰ ਬਿੰਦੂ ਤੋਂ ਇੱਕ ਇਮਾਰਤ ਦੇ ਸਿਖ਼ਰ ਦਾ ਉੱਚਾਣ ਕੋਣ 30° ਹੈ ਅਤੇ ਇਮਾਰਤ ਦੇ ਆਧਾਰ ਬਿੰਦੂ ਤੋਂ ਮੀਨਾਰ ਦੇ ਸਿਖਰ ਦਾ ਉੱਚਾਣ ਕੋਣ 60° ਹੈ । ਜੇਕਰ ਮੀਨਾਰ 50 ਮੀਟਰ ਉੱਚੀ ਹੋਵੇ ਤਾਂ ਇਮਾਰਤ ਦੀ ਉੱਚਾਈ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਮੰਨ ਲਉ BC = 50 m ਮੀਨਾਰ ਦੀ ਉੱਚਾਈ ਹੈ AD = hm ਇਮਾਰਤ ਦੀ ਉੱਚਾਈ ਹੈ । ਮੀਨਾਰ ਦੇ ਆਧਾਰ ਬਿੰਦੂ ਤੋਂ ਇਮਾਰਤ ਦੇ ਸਿਖ਼ਰ ਤੱਕ ਅਤੇ ਇਮਾਰਤ ਦੇ ਆਧਾਰ ਬਿੰਦੂ ਤੋਂ ਮੀਨਾਰ ਦੇ ਸਿਖ਼ਰ ਦੇ ਉੱਚਾਣ ਕੋਣ ਕ੍ਰਮਵਾਰ 30° ਅਤੇ 60° ਹਨ । (ਦੇਖੋ ਚਿੱਤਰ)

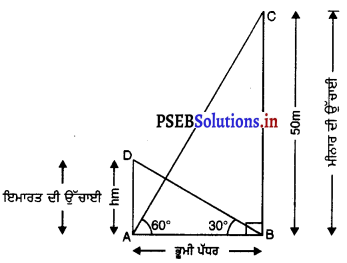
ਸਮਕੋਣ △ABC ਵਿੱਚ,
\(\frac{AB}{BC}\) = cot 60°
ਜਾਂ \(\frac{AB}{50}\) = \(\frac{1}{\sqrt{3}}\)
ਜਾਂ AB = \(\frac{50}{\sqrt{3}}\) …(1)
ਸਮਕੋਣ △DAB ਵਿੱਚ,
\(\frac{AB}{DA}\) = cot 30°
ਜਾਂ \(\frac{AB}{h}\) = \(\sqrt {3}\)
ਜਾਂ AB = h\(\sqrt {3}\) …(2)
(1) ਅਤੇ (2), ਤੋਂ ,
\(\frac{50}{\sqrt{3}}\) = h \(\sqrt {3}\)
ਜਾਂ \(\frac{50}{\sqrt{3}}\) \(\frac{1}{\sqrt{3}}\) = h
ਜਾਂ h = \(\frac{50}{3}\) = 16∙6666
ਜਾਂ h = 16∙70 m (ਲਗਭਗ
∴ ਇਮਾਰਤ ਦੀ ਉੱਚਾਈ 16-70 m ਹੈ ।

ਪ੍ਰਸ਼ਨ 10.
ਇੱਕ 80 ਮੀਟਰ ਚੌੜੀ ਸੜਕ ਦੇ ਦੋਵਾਂ ਪਾਸਿਆਂ ‘ਤੇ ਆਹਮਣੇ-ਸਾਹਮਣੇ ਬਰਾਬਰ ਲੰਬਾਈ ਵਾਲੇ ਦੋ ਖੰਬੇ ਲੱਗੇ ਹੋਏ ਹਨ । ਇਹਨਾਂ ਦੋਹਾਂ ਖੰਬਿਆਂ ਦੇ ਵਿੱਚ ਸੜਕ ‘ਤੇ ਇੱਕ ਬਿੰਦੂ ਤੋਂ ਖੰਬਿਆਂ ਦੇ ਸਿਖ਼ਰਾਂ ਦੇ ਉੱਚਾਣ ਕੋਣ ਕੁਮਵਾਰ 60° ਅਤੇ 30° ਹੈ । ਖੰਬਿਆਂ ਦੀ ਉੱਚਾਈ ਅਤੇ ਖੰਬਿਆਂ ਤੋਂ ਬਿੰਦੁ ਦੀ ਦੂਰੀ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਮੰਨ ਲਉ BC = DE = hm ਦੋ ਬਰਾਬਰ ਲੰਬਾਈ ਵਾਲੇ ਖੰਬਿਆਂ ਦੀ ਉੱਚਾਈ ਹੈ ਅਤੇ ਬਿੰਦੂ A ਲੋੜੀਂਦਾ ਬਿੰਦੂ ਹੈ, ਜਿੱਥੇ ਦੋਹਾਂ ਖੰਬਿਆ ਦੇ ਉੱਚਾਣ ਕੋਣ ਕੁਮਵਾਰ 30° ਅਤੇ 60° ਹੈ । (ਦੇਖੋ ਚਿੱਤਰ)

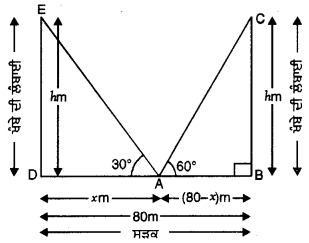
ਸਮਕੋਣ △ADE ਵਿੱਚ,
\(\frac{ED}{DA}\) = tan 30°
ਜਾਂ \(\frac{h}{x}\) = \(\frac{1}{\sqrt{3}}\)
ਜਾਂ h = \(\frac{h}{\sqrt{3}}\) ….(1)
ਸਮਕੋਣ △ABC ਵਿੱਚ,
\(\frac{BC}{AB}\) = tan 60°
ਜਾਂ \(\frac{h}{80-x}\) = \(\sqrt {3}\)
ਜਾਂ h = (80 – x)\(\sqrt {3}\)
(1) ਅਤੇ (2) ਤੋਂ
\(\frac{x}{\sqrt{3}}\) = (80 – x)\(\sqrt {3}\)
ਜਾਂ x = (80 – x)\(\sqrt {3}\) × \(\sqrt {3}\)
ਜਾਂ x = (80 – x) 3
ਜਾਂ x = 240 – 3x
ਜਾਂ 4x = 240
ਜਾਂ x = \(\frac{240}{4}\) = 60
x ਦਾ ਮੁੱਲ (1) ਵਿੱਚ ਰੱਖਣ ‘ਤੇ
h = \(\frac{60}{\sqrt{3}}\) = \(\frac{60}{\sqrt{3}}\) × \(\frac{\sqrt{3}}{\sqrt{3}}\)
= \(\frac{60 \sqrt{3}}{3}\) = 20\(\sqrt {3}\)
= (20 × 1.732) m = 34.64 m
∴ DA = x = 60 m
ਅਤੇ AB = 80 – x = (80 – 60) m = 20m.
∴ ਹਰੇਕ ਖੰਬੇ ਦੀ ਉੱਚਾਈ 34:64 m ਅਤੇ ਖੰਬਿਆਂ ਤੋਂ ਬਿੰਦੁ ਦੀ ਦੂਰੀ 20 m ਅਤੇ 60 m ਹੈ ।

ਪ੍ਰਸ਼ਨ 11.
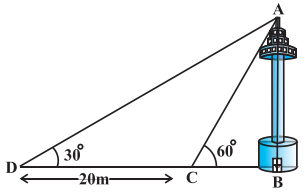
ਇੱਕ ਨਹਿਰ ਦੇ ਇੱਕ ਤੱਟ ‘ਤੇ ਇੱਕ ਟੀ. ਵੀ. ਟਾਵਰ ਸਿੱਧਾ ਖੜਾ ਹੈ । ਟਾਵਰ ਦੇ ਠੀਕ ਸਾਹਮਣੇ ਦੂਸਰੇ ਤੱਟ ‘ਤੇ ਇੱਕ ਹੋਰ ਬਿੰਦੂ ਤੋਂ ਟਾਵਰ ਦੇ ਸਿਖ਼ਰ ਦਾ ਉੱਚਾਣ ਕੋਣ 60° ਹੈ । ਇਸੇ ਤੱਟ ‘ਤੋਂ ਇਸ ਬਿੰਦੂ ਤੋਂ 20 m ਦੂਰ ਅਤੇ ਇਸ ਬਿੰਦੂ ਨੂੰ ਮੀਨਾਰ ਦੇ ਆਧਾਰ ਬਿੰਦੂ ਨਾਲ ਮਿਲਾਉਣ ਵਾਲੀ ਰੇਖਾ ‘ ਤੇ ਸਥਿਤ ਇੱਕ ਹੋਰ ਬਿੰਦੂ ਤੋਂ ਟਾਵਰ ਦੇ ਸਿੱਖ਼ਰ ਦਾ ਉੱਚਾਣ ਕੋਣ 30° ਹੈ (ਦੇਖੋ ਚਿੱਤਰ ਟਾਵਰ ਦੀ ਉੱਚਾਈ ਅਤੇ ਨਹਿਰ ਦੀ ਚੌੜਾਈ ਪਤਾ ਕਰੋ ।

ਹੱਲ:
ਮੰਨ ਲਉ BC = x m ਨਹਿਰ ਦੀ ਚੌੜਾਈ ਹੈ ਅਤੇ AB= hm ਟੀ.ਵੀ. ਟਾਵਰ ਦੀ ਉੱਚਾਈ ਹੈ | ਅਲੱਗਅਲੱਗ ਸਥਿਤੀਆਂ ਵਿਚ ਟਾਵਰ ਦੇ ਉੱਚਾਣ ਕੋਣ ਕ੍ਰਮਵਾਰ 30° ਅਤੇ 60° ਹਨ ।
(ਦੇਖੋ ਚਿੱਤਰ)

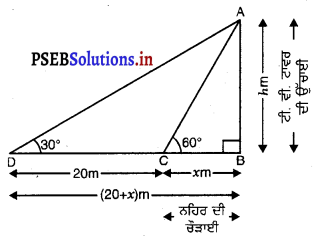
ਸਮਕੋਣ △ABC ਵਿੱਚ,
\(\frac{AB}{BC}\) = tan 60°
ਜਾਂ \(\frac{h}{x}\) = \(\sqrt {3}\)
ਜਾਂ h = \(\sqrt {3}\)x …(1)
ਨਾਲ ਹੀ, ਸਮਕੋਣ △ABD ਵਿੱਚ,
\(\frac{AB}{AD}\) = tan 30°
ਜਾਂ \(\frac{h}{20+x}\) = \(\frac{1}{\sqrt{3}}\)
ਜਾਂ h = \(\frac{20+x}{\sqrt{3}}\) …..(2)
(1) ਅਤੇ (2) ਤੋਂ
\(\sqrt {3}\)x = \(\frac{20+x}{\sqrt{3}}\)
ਜਾਂ \(\sqrt {3}\)(\(\sqrt {3}\)x) = 20 + x
ਜਾਂ 3x = 20 + x
ਜਾਂ 2x = 20
ਜਾਂ x = \(\frac{20}{2}\) = 10
x ਦਾ ਮੁੱਲ (1) ਵਿਚ ਭਰਨ ਤੇ
h= 10(\(\sqrt {3}\)).
= 10 × 1∙732
h= 17∙32 m
∴ ਟੀ.ਵੀ. ਟਾਵਰ ਦੀ ਉੱਚਾਈ 17:32 m ਹੈ ਅਤੇ ਨਹਿਰ ਦੀ ਚੌੜਾਈ 10 m. ਹੈ ।

ਪ੍ਰਸ਼ਨ 12.
7m ਉੱਚੀ ਇਮਾਰਤ ਦੇ ਸਿਖ਼ਰ ਤੋਂ ਇੱਕ ਕੇਬਲ ਟਾਵਰ ਦੇ ਸਿਖ਼ਰ ਦਾ ਉੱਚਾਣ ਕੋਣ 60° ਹੈ ਅਤੇ ਇਸਦੇ ਪੈਰ ਦਾ ਨੀਵਾਨ ਕੋਣ 45° ਹੈ। ਟਾਵਰ ਦੀ ਉੱਚਾਈ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਮੰਨ ਲਉ BD = hm ਕੇਵਲ ਟਾਵਰ ਦੀ ਉੱਚਾਈ ਹੈ ਅਤੇ AE = 7 m ਇਮਾਰਤ ਦੀ ਉੱਚਾਈ ਹੈ । ਕੇਵਲ ਟਾਵਰ ਦੇ ਸਿਖਰ ਦਾ ਉੱਚਾਣ ਕੋਣ ਅਤੇ ਪੈਰ ਦਾ ਨੀਵਾਨ ਕੋਣ ਕੁਮਵਾਰ 60° ਅਤੇ 45° ਹੈ ।
(ਦੇਖੋ ਚਿੱਤਰ)

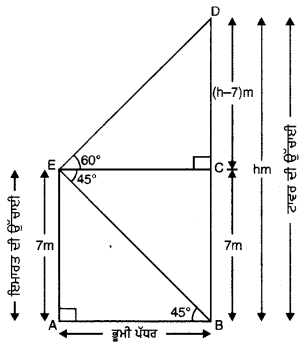
ਸਮਕੋਣ △BAE ਵਿੱਚ
\(\frac{AB}{AE}\) = cot 45°
ਜਾਂ \(\frac{AB}{7}\) = 1
ਜਾਂ AB = 7 m …..(1)
ਸਮਕੋਣ △DCE ਵਿੱਚ
\(\frac{EC}{DC}\) = cot 60°
ਜਾਂ \(\frac{EC}{h-7}\) = \(\frac{1}{\sqrt{3}}\)
ਜਾਂ EC = \(\frac{h-7}{\sqrt{3}}\) …(2)
ਪਰ AB = EC …(ਦਿੱਤਾ ਹੈ।)
7 = \(\frac{h-7}{\sqrt{3}}\)
[(1) ਅਤੇ (2) ਤੋਂ।]
ਜਾਂ 7\(\sqrt {3}\) = h – 7
ਜਾਂ h = 7\(\sqrt {3}\) + 7 = 7 (\(\sqrt {x}\) + 1)
ਜਾਂ h = 7(1∙732 + 1) = 7(2∙732)
ਜਾਂ h = 19∙124
ਜਾਂ h = 19∙20 m (ਲਗਭਗ)
∴ ਕੇਬਲ ਟਾਵਰ ਦੀ ਉੱਚਾਈ 19.20 m ਹੈ ।

ਪ੍ਰਸ਼ਨ 13.
ਸਮੁੰਦਰ ਤਲ ਤੋਂ 75 m ਉੱਚੇ ਲਾਈਟ ਹਾਊਸ ਦੇ ਸਿਖ਼ਰ ਤੋਂ ਦੇਖਣ ਨਾਲ ਦੋ ਸਮੁੰਦਰੀ ਜਹਾਜ਼ਾਂ ਦੇ ਨੀਵਾਨ ਕੋਣ ਕੁਮਵਾਰ 30° ਅਤੇ 45° ਹਨ । ਜੇਕਰ ਲਾਈਟ ਹਾਊਸ ਦੇ ਇੱਕ ਹੀ ਪਾਸੇ ਤੋਂ ਇੱਕ ਜਹਾਜ਼ ਦੂਸਰੇ ਜਹਾਜ਼ ਦੇ ਬਿਲਕੁਲ ਪਿੱਛੇ ਹੋਵੇ ਤਾਂ ਦੋਵੇਂ ਜਹਾਜ਼ਾਂ ਦੀ ਵਿਚਕਾਰਲੀ ਦੂਰੀ ਪਤਾ ਕਰੋ ।
ਹੱਲ:

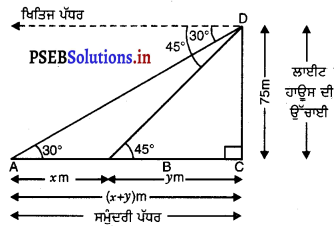
ਮੰਨ ਲਉ CD = 75 m ਲਾਈਟ ਹਾਊਸ ਦੀ ਉੱਚਾਈ | ਅਤੇ ਲਾਈਟ ਹਾਊਸ ਦੇ ਸਿਖ਼ਰ ਦੇ ਬਿੰਦੁ ਤੋਂ ਜਹਾਜਾਂ ਦੇ | ਨੀਵਾਨ ਕੋਣ ਕ੍ਰਮਵਾਰ 30° ਅਤੇ 45° ਹੈ ।
(ਦੇਖੋ ਚਿੱਤਰ)
ਸਮਕੋਣ △BCD ਵਿੱਚ,
\(\frac{BC}{CD}\) = cot 45°
ਜਾਂ \(\frac{y}{75}\) = 1
ਜਾਂ y = 75 m ….(1)
ਸਮਕੋਣ △ACD ਵਿੱਚ,
\(\frac{AC}{CD}\) = cot 30°
ਜਾਂ \(\frac{x+y}{75}\) = \(\sqrt {3}\)
ਜਾਂ x + y = 75\(\sqrt {3}\)
ਜਾਂ x + 75 = 75\(\sqrt {x}\)
[1) ਦਾ ਪ੍ਰਯੋਗ ਕਰਨ ਤੋਂ]
ਜਾਂ x = 75\(\sqrt {x}\) – 75
= 75 (\(\sqrt {x}\) – 1)
= 75 (1∙732 – 1)
= 75 (0∙732)
x = 54∙90
∴ ਦੋਵੇਂ ਜਹਾਜਾਂ ਵਿਚਕਾਰਲੀ ਦੂਰੀ 54∙90 m ਹੈ ।

ਪ੍ਰਸ਼ਨ 14.
1.2 m ਲੰਬੀ ਇੱਕ ਲੜਕੀ ਜਮੀਨ ਤੋਂ 88.2 m ਦੀ ਉੱਚਾਈ ‘ਤੇ ਇੱਕ ਖਿਤਿਜੇ ਰੇਖਾ ਵਿੱਚ ਉੱਡ ਰਹੇ ਗੁਬਾਰੇ ਨੂੰ ਦੇਖਦੀ ਹੈ । ਕਿਸੇ ਵੀ ਸਮੇਂ ਲੜਕੀ ਦੀ ਅੱਖ ਨਾਲ ਗੁਬਾਰੇ ਦਾ ਉੱਚਾਣ ਕੋਣ 60° ਹੈ । ਕੁੱਝ ਸਮੇਂ ਬਾਅਦ ਉੱਚਾਣ ਕੋਣ ਘੱਟ ਕੇ 30° ਹੋ ਜਾਂਦਾ ਹੈ ਦੇਖੋ ਚਿੱਤਰ) । ਇਸ ਅੰਤਰਾਲ ਦੌਰਾਨ ਗੁਬਾਰੇ ਦੁਆਰਾ ਤੈਅ ਕੀਤੀ ਦੂਰੀ ਪਤਾ ਕਰੋ ।

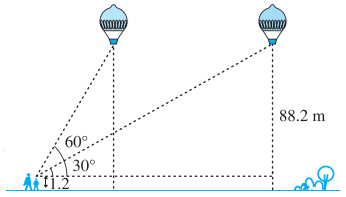
ਹੱਲ:
ਮੰਨ ਲਉ 1.2 m ਲੰਬੀ ਲੜਕੀ ਦੀ ਸਥਿਤੀ ‘A’ ਹੈ । ਇਸ ਬਿੰਦੂ ਤੋਂ ਗੁਬਾਰੇ ਦੇ ਉੱਚਾਣ ਕੋਣ ਕ੍ਰਮਵਾਰ 30° ਅਤੇ 60° ਹਨ । ਨਾਲ ਹੀ
BE = CD = 88.2 m ਗੁਬਾਰੇ ਦੀ ਉੱਚਾਈ ਹੈ।
(ਦੇਖੋ ਚਿੱਤਰ)

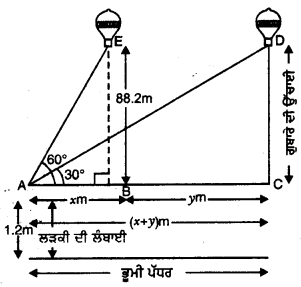
ਸਮਕੋਣ △ABE ਵਿੱਚ,
\(\frac{AB}{BE}\) = cot 60°
ਜਾਂ \(\frac{x}{88.2}\) = \(\frac{1}{\sqrt{3}}\)
ਜਾਂ x = \(\frac{88.2}{\sqrt{3}}\) m …(1)
ਸਮਕੋਣ △ACD ਵਿੱਚ
\(\frac{AC}{CD}\) = cot 30°
ਜਾਂ \(\frac{x+y}{88.2}\) = \(\sqrt {3}\)
ਜਾਂ x + y = 88.2\(\sqrt {3}\)
ਜਾਂ \(\frac{88.2}{\sqrt{3}}\) + y = 88.2\(\sqrt {3}\)
ਜਾਂ y = 88.2\(\sqrt {3}\) = \(\frac{88.2}{\sqrt{3}}\)
ਜਾਂ y = 88.2[\(\sqrt {3}\) – \(\frac{1}{\sqrt{3}}\)]
ਜਾਂ y = 88.2[latex]\frac{3-1}{\sqrt{3}}[/latex] × \(\frac{\sqrt{3}}{\sqrt{3}}\)
ਜਾਂ y = \(\frac{88.2 \times 2 \times \sqrt{3}}{3}\)
ਜਾਂ y = 58.8\(\sqrt {3}\) m
ਜਾਂ y = 58.8 (1.732) = 101.8416 m
ਜਾਂ y = 101.90 m
∴ ਗੁਬਾਰੇ ਦੁਆਰਾ ਤੈਅ ਕੀਤੀ ਗਈ ਦੂਰੀ 101.90 m. ਹੈ ।

ਪ੍ਰਸ਼ਨ 15.
ਇੱਕ ਸਿੱਧਾ ਰਾਜ ਮਾਰਗ ਇੱਕ ਮੀਨਾਰ ਦੇ ਆਧਾਰ ਤੱਕ ਜਾਂਦਾ ਹੈ । ਮੀਨਾਰ ਦੇ ਸਿਖ਼ਰ ‘ ਤੇ ਖੜਾ ਇੱਕ ਆਦਮੀ ਇੱਕ ਕਾਰ ਨੂੰ 30° ਨੀਵਾਨ ਕੋਣ ‘ਤੇ ਦੇਖਦਾ ਹੈ, ਜੋ ਮੀਨਾਰ ਦੇ ਆਧਾਰ ਵੱਲ ਇੱਕ ਸਮਾਨ ਚਾਲ ਨਾਲ ਆ ਰਹੀ ਹੈ । ਛੇ ਸੈਕਿੰਡ ਬਾਅਦ ਕਾਰ ਦਾ ਨੀਵਾਨ ਕੋਣ 60° ਹੋ ਗਿਆ । ਇਸ ਬਿੰਦੂ ਤੋਂ ਮੀਨਾਰ ਦੇ ਆਧਾਰ ਤੱਕ ਪਹੁੰਚਣ ਲਈ ਕਾਰ ਦੁਆਰਾ ਲਿਆ ਗਿਆ ਸਮਾਂ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਮੰਨ ਲਉ CD = hm ਮੀਨਾਰ ਦੀ ਉੱਚਾਈ ਹੈ । ਮੰਨ ਲਉ A’ ਕਾਰ ਦੀ ਪਹਿਲੀ ਸਥਿਤੀ ਹੈ ਅਤੇ ਛੇ ਸੈਕਿੰਡ ਦੇ ਬਾਅਦ ਕਾਰ B ਤੱਕ ਪਹੁੰਚ ਜਾਂਦੀ ਹੈ । A ਅਤੇ B ਉੱਤੇ ਕਾਰ ਦੇ ਨੀਵਾਨ ਕੋਣ 30° ਅਤੇ 60° ਹਨ ।
(ਦੇਖੇ ਚਿੱਤਰ)

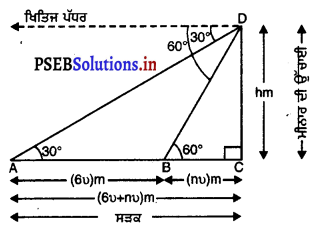
ਮੰਨ ਲਉ ਕਾਰ ਦੀ ਚਾਲ v ਮੀਟਰ ਪ੍ਰਤੀ ਸੈਕਿੰਡ ਹੈ ਸੂਤਰ ਦੂਰੀ = ਚਾਲ × ਸਮਾਂ ਦਾ ਪ੍ਰਯੋਗ ਕਰਕੇ
AB = ਕਾਰਾਂ ਦੁਆਰਾ 6 ਸੈਕਿੰਡ ਵਿੱਚ ਤੈਅ ਕੀਤੀ ਗਈ ਦੂਰੀ
AB = 6v ਮੀਟਰ
ਕਾਰ ਦੁਆਰਾ ਮੀਨਾਰ ਤੱਕ ਪਹੁੰਚਣ ਵਿਚ ਲਿਆ ਗਿਆ ਸਮਾਂ ‘n’ ਸੈਕਿੰਡ ਹੈ ।
∴ BC = nv ਮੀਟਰ
ਸਮਕੋਣ △ACD ਵਿੱਚ
\(\frac{CD}{AC}\) = tan 30°
ਜਾਂ \(\frac{h}{6v+nv}\) = \(\frac{1}{\sqrt{3}}\)
ਜਾਂ h = \(\frac{6v+nv}{\sqrt{3}}\) …(1)
ਸਮਕੋਣ △BCD ਵਿੱਚ,
\(\frac{CD}{BC}\) = tan 60°
ਜਾਂ \(\frac{h}{nv}\) = \(\sqrt {3}\)
ਜਾਂ h = nv(\(\sqrt {3}\) ) ….(2)
(1) ਅਤੇ (2) ਤੋਂ ਸਾਨੂੰ ਮਿਲਦਾ ਹੈ।
ਜਾਂ \(\frac{6v+nv}{\sqrt{3}}\) = nv(\(\sqrt {3}\))
ਜਾਂ 6v + nv = nv(\(\sqrt {3}\) × \(\sqrt {3}\))
ਜਾਂ 6v + nv = 3nv ਜਾਂ 6v = 2nv
ਜਾਂ n = \(\frac{6v}{2v}\) = 3
ਮੀਨਾਰ ਦੇ ਆਧਾਰ ਤੱਕ ਪਹੁੰਚਣ ਲਈ ਕਾਰ ਦੁਆਰਾ ਲਿਆ ਗਿਆ ਸਮਾਂ 3 ਸੈਕਿੰਡ ਹੈ ।

ਪ੍ਰਸ਼ਨ 16.
ਮੀਨਾਰ ਦੇ ਆਧਾਰ ‘ਤੇ ਇੱਕ ਸਰਲ ਰੇਖਾ 4m ਅਤੇ 9 m ਦੀ ਦੂਰੀ ‘ਤੇ ਸਥਿਤ ਦੋ ਬਿੰਦੁਆਂ ਤੋਂ ਮੀਨਾਰ ਦੇ ਸਿਖ਼ਰ ਦੇ ਉੱਚਾਣ ਕੋਣ ਪੂਰਕ ਕੋਣ ਹਨ। ਸਿੱਧ ਕਰੋ ਕਿ ਮੀਨਾਰ ਦੀ ਉੱਚਾਈ 6 m ਹੈ ।
ਹੱਲ:
ਮੰਨ ਲਉ CD = h m ਮੀਨਾਰ ਦੀ ਉਚਾਈ ਹੈ। ਅਤੇ B; Aਲੋਂੜੀਂਦੇ ਬਿੰਦੂ ਹਨ ਜੋ ਮੀਨਾਰ ਤੋਂ ਕ੍ਰਮਵਾਰ 4 m ਅਤੇ 9 m ਦੀ ਦੂਰੀ ‘ਤੇ ਹਨ ।
(ਦੇਖੋ ਚਿੱਤਰ)

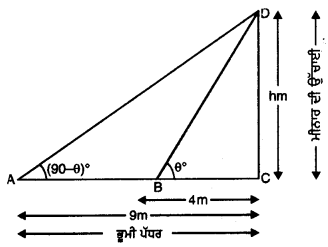
ਸਮਕੋਣ △BCD ਵਿੱਚ,
\(\frac{CD}{BC}\) = tan θ
ਜਾਂ \(\frac{h}{4}\) = tan θ …(1)
ਨਾਲ ਹੀ, ਸਮਕੋਣ △ACD ਵਿੱਚ,
\(\frac{CD}{AC}\) = tan (90 – θ)
\(\frac{h}{9}\) = cot θ …(2)
(1) ਅਤੇ (2) ਨੂੰ ਗੁਣਾ ਕਰਨ ‘ਤੇ
\(\frac{h}{4}\) × \(\frac{h}{9}\) = tan θ × cot θ
ਜਾਂ \(\frac{h^{2}}{36}\) = tan θ × \(\frac{1}{\tan \theta}\)
ਜਾਂ h² = 36 = (6)²
ਜਾਂ h= 6
∴ ਮੀਨਾਰ ਦੀ ਉੱਚਾਈ 6 m ਹੈ