PSEB 10th Class Science Important Questions Chapter 10 प्रकाश-परावर्तन तथा अपवर्तन

Punjab State Board PSEB 10th Class Science Important Questions Chapter 10 प्रकाश-परावर्तन तथा अपवर्तन Important Questions and Answers.

PSEB 10th Class Science Important Questions Chapter 10 प्रकाश-परावर्तन तथा अपवर्तन

दीर्घ उत्तरात्मक प्रश्न (Long Answer Type Questions)

प्रश्न 1.
अवतल दर्पण के सम्मुख विभिन्न स्थितियों में रखी वस्तु के दर्पण द्वारा बने प्रतिबिंबों की स्थिति, प्रकृति एवं आकार चित्र द्वारा स्पष्ट कीजिए ।
उत्तर-
अवतल दर्पण द्वारा प्रतिबिंब का बनना-अवतल दर्पण द्वारा बने प्रतिबिंब की स्थिति, प्रकृति एवं आकार दर्पण से वस्तु की दूरी पर निर्भर करती है।
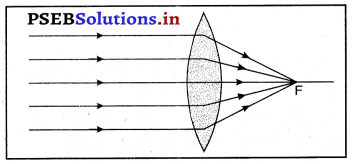
(i) जब वस्तु अनंत दूरी पर है-मान लो अनंत दूरी पर रखी वस्तु AB से चलने वाली किरणें परस्पर समांतर होती हैं। एक किरण, जो फोकस F से होकर जाती है, परावर्तन के पश्चात् मुख्य अक्ष के समांतर हो जाती है। दूसरी किरण, जो वक्रता केंद्र C से होकर आती है, परावर्तन के पश्चात् उसी मार्ग पर लौट जाती है। ये दोनों परावर्तित किरणें दर्पण के फोकस तल के बिंदु B पर मिलती हैं। अत : B’, B का प्रतिबिंब हैं तथा A का प्रतिबिंब A.’ फोकस F पर बनता है। इस प्रकार AB वस्तु का प्रतिबिंब A B’ बनता है।
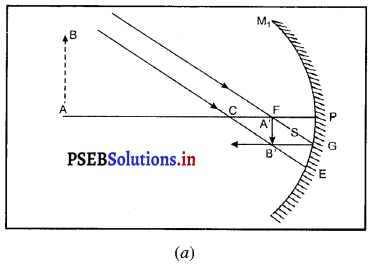
PSEB 10th Class Science Important Questions Chapter 10 प्रकाश-परावर्तन तथा अपवर्तन 1

यह प्रतिबिंब अवतल दर्पण के फोकस पर स्थित है तथा वास्तविक, उल्टा एवं वस्तु से आकार में बहुत छोटा बनता है।
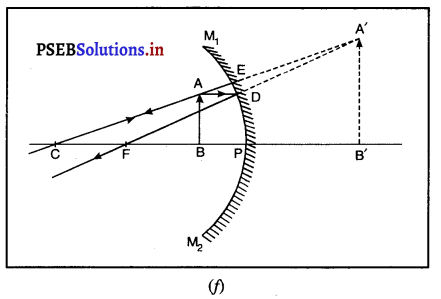
(ii) जब वस्तु अनंत एवं वक्रता केंद्र (C) के मध्य रखी हो-मान लो वस्तु AB, अवतल दर्पण के सम्मुख उसकी वक्रता-त्रिज्या से अधिक दूरी पर रखी है। बिंदु A से मुख्य अक्ष के समांतर चलने वाली किरण AE, परावर्तन के पश्चात् फोकस F से होकर जाती है। दूसरी किरण AG जो वक्रता केंद्र C से होकर जाती है परावर्तन के पश्चात उसी मार्ग से लौट आती है। ये दोनों परावर्तित किरणें A’ पर मिलती हैं, जो A का वास्तविक प्रतिबिंब है। A’ से मुख्य अक्ष पर खींचा गया लंब A’B’, वस्तु AB का प्रतिबिंब है।
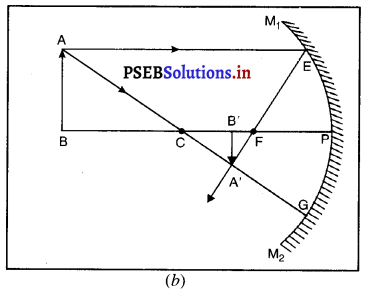
PSEB 10th Class Science Important Questions Chapter 10 प्रकाश-परावर्तन तथा अपवर्तन 2
यह प्रतिबिंब दर्पण के वक्रता केंद्र C तथा मुख्य फोकस F के बीच में वास्तविक, उल्टा और वस्तु से छोटा बनता है।

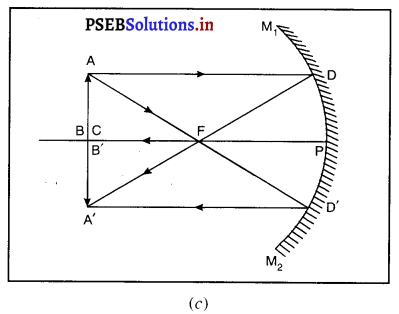
(iii) जब वस्तु वक्रता-केंद्र (C) पर रखी हो-मान लो वस्तु AB, अवतल दर्पण के वक्रता केंद्र C पर रखी है। A से मुख्य अक्ष के समांतर चलने वाली आपतित किरण AD, परावर्तित होकर फोकस F से होकर जाती है । दूसरी आपतित किरण AD’, फोकस F से में से होकर जाती है जो परावर्तन के पश्चात् मुख्य अक्ष के समांतर D’A’ बन जाती है। ये दोनों किरणें बिंदु A’ पर मिलती हैं। A’ का वास्तविक प्रतिबिंब हैं। A’ से मुख्य अक्ष पर खींचा गया लंब A’B’, वस्तु AB का प्रतिबिंब हैं।
यह प्रतिबिंब दर्पण के वक्रता केंद्र पर वस्तु के समान आकार का, वास्तविक तथा उल्टा है।
PSEB 10th Class Science Important Questions Chapter 10 प्रकाश-परावर्तन तथा अपवर्तन 3
(iv) जब वस्तु वक्रता केंद्र (C) तथा फोकस (F) के बीच रखी होमान लो वस्तु AB, दर्पण के मुख्य फोकस F तथा वक्रता केंद्र C के बीच में स्थित हैं। A से मुख्य अक्ष के समांतर चलने वाली किरण AD, परावर्तित होकर मुख्य फोकस F से होकर जाती है। दूसरी आपतित किरण AD’, जो मुख्य अक्ष के समांतर हो जाती है। ये दोनों परावर्तित किरणें एक-दूसरे को A’ पर काटती हैं जो A का प्रतिबिंब हैं। A’ से मुख्य अक्ष पर खींचा गया लम्ब A’,B’ वस्तु AB का प्रतिबिंब है।
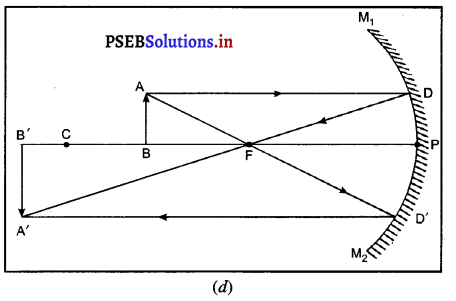
PSEB 10th Class Science Important Questions Chapter 10 प्रकाश-परावर्तन तथा अपवर्तन 4
यह प्रतिबिंब दर्पण के वक्रता केंद्र तथा अनंत के बीच बनता है एवं वास्तविक उल्टा व वस्तु से बड़ा है।

(v) जब वस्तु मुख्य फोकस (F) पर रखी हो-मान लो वस्तु AB, मुख्य फोकस F पर स्थित है। A से मख्य अक्ष के समांतर चलने वाली आपतित किरण AD, परावर्तित होकर मुख्य फोकस F से होकर जाती है। बिंदु A से चलने वाली दूसरी आपतित किरण AE जो पीछे बढ़ाने पर वक्रता केंद्र C से गुजरती है, दर्पण से परावर्तित होकर उसी मार्ग पर लौट आती है। ये दोनों परावर्तित किरणें समांतर होने के कारण अनंत पर मिलती हैं।
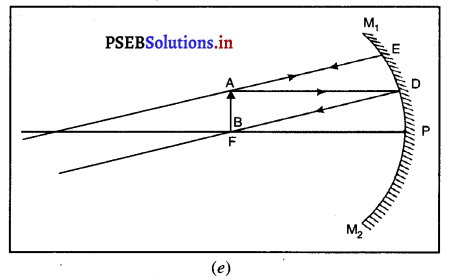
PSEB 10th Class Science Important Questions Chapter 10 प्रकाश-परावर्तन तथा अपवर्तन 5
यह प्रतिबंब अनंत पर बनता है तथा वास्तविक, उल्टा व वस्तु से बड़ा होता है।

(vi) जब वस्तु ध्रुव (P) तथा फोकस (F) के बीच रखी हो-मान लो वस्तु AB, अवतल दर्पण के फोकस एवं ध्रुव के बीच स्थित है। इसमें A से मुख्य अक्ष के समांतर चलने वाली किरण AD, परावर्तित होकर मुख्य फोकस F से होकर जाती है। दूसरी किरण AE दर्पण पर लंबवत् गिरती हैं। जो यह परावर्तित होकर उसी मार्ग पर लौट आती है। ये दोनों परावर्तित किरणें दर्पण के पीछे A’ से आती हुई प्रतीत होती हैं। अंत : A’, बिंदु A का आभासी प्रतिबिंब हैं। A’ से मुख्य अक्ष पर खींचा गया लंब AB’ वस्तु AB का प्रतिबिंब है।
PSEB 10th Class Science Important Questions Chapter 10 प्रकाश-परावर्तन तथा अपवर्तन 6
यह प्रतिबिंब दर्पण के पीछे, आभासी, सीधा व आकार में वस्तु से बड़ा होता है।

प्रश्न 2.
प्रकाश अपवर्तन किसे कहते हैं ? काँच की आयताकार स्लैब में प्रकाश अपवर्तन चित्र द्वारा समझाओ तथा यह दर्शाओ कि निर्गत किरण, आपतित किरण के समांतर होती है।
उत्तर-
प्रकाश अपवर्तन- जब प्रकाश की किरण एक माध्यम से दूसरे माध्यम में प्रवेश करती है तो वह दो माध्यमों के मिलन तल पर अपना पथ बदल लेती है। प्रकाश की इस प्रक्रिया को प्रकाश का अवपर्तन कहते हैं।
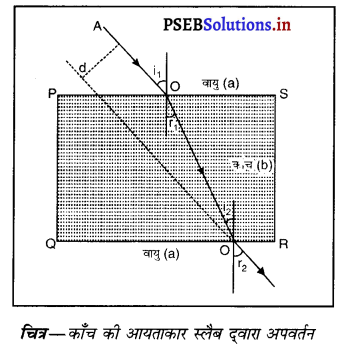
PSEB 10th Class Science Important Questions Chapter 10 प्रकाश-परावर्तन तथा अपवर्तन 7
एक आयताकार काँच की स्लैब PQRS को वायु में रखा गया है। AO आपतित किरण, 00′ अपवर्तित किरण और O’ B निर्गत किरण है। जब प्रकाश वायु में से काँच में प्रवेश करती है तो बिंदु 0 पर स्नैल के नियम का प्रयोग करने पर
\(\frac{\sin i_{1}}{\sin r_{1}}\) = a_µ_b ……………….(1)
अब प्रकाश किरण काँच (सघन माध्यम) से वायु (विरल माध्यम) में जा रही है। बिंदु O’ पर स्नैल के नियम का प्रयोग करने पर
b_µ_a= \(\frac{\sin i_{2}}{\sin r_{2}}=\frac{\sin r_{1}}{\sin r_{2}}\) ………………..(2)
(∵ ∠i₂ = ∠r₁ )
प्रकाश के उत्क्रमणीयता सिद्धांत (Principal of reversibility of light) के अनुसार
b_µ_a = \(\frac{1}{a_{u_{b}}}\) …………………………….. (3)
समीकरण (2) और (3) से
a_µ_b = \(\frac{\sin r_{2}}{\sin r_{1}}\) ………………………………………. (4)
समीकरण (1) और (4) की तुलना करने पर
\(\frac{\sin i_{1}}{\sin r_{1}}=\frac{\sin r_{2}}{\sin r_{1}}\)
या
sin i₁ = sin r₂
∴ i₁ =r₂
इसका अर्थ है कि आपतन कोण निर्गमन कोण के समान है । इसलिए जब प्रकाश एक आयताकार काँच की स्लैब से अपवर्तन होता है, तो निर्गत किरण और आपतित किरण समांतर होती हैं।

प्रश्न 3.
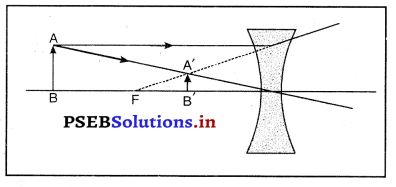
जब किसी वस्तु को एक उत्तल लेंस से (i) F और 2F के बीच (ii) 2F से परे (ii) F पर रखा जाता है तो चित्र की सहायता से इसके प्रतिबिंब की रचना दर्शाओ।
अथवा
एक वस्तु किसी उत्तल लेंस के F पर रखी हैं। चित्र की सहायता से उत्तल लेंस से बने प्रतिबिंब की स्थिति, आकार और स्वरूप ज्ञात कीजिए ।
उत्तर-
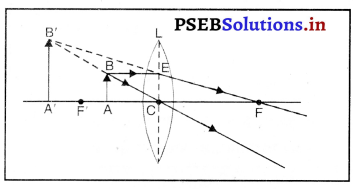
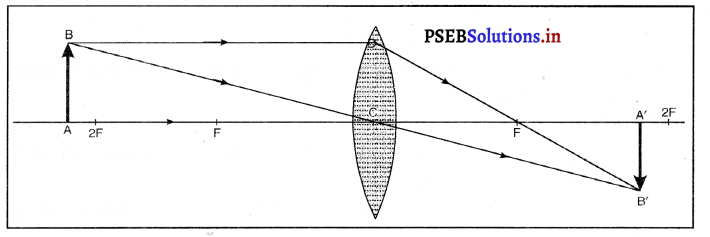
(i) जब वस्तु F और 2F के मध्य हो-जब वस्तु उत्तल लेंस के F तथा 2F के मध्य रखी जाती है तो प्रतिबिंब लेंस के दूसरी तरफ 2F से परे बनता है। यह प्रतिबिंब वास्तविक, उल्टा तथा बड़े आकार का बनता है।
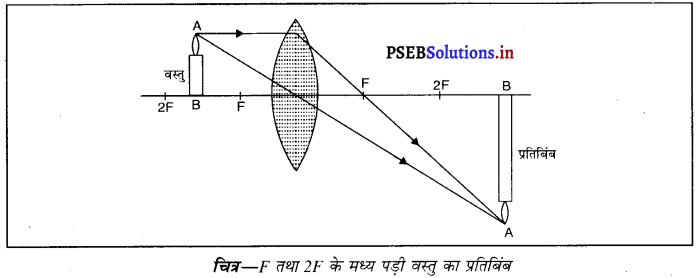
PSEB 10th Class Science Important Questions Chapter 10 प्रकाश-परावर्तन तथा अपवर्तन 8
(ii) जब वस्तु 2F से परे (दूर) पड़ी हो-जब वस्तु उत्तल लेंस के सामने 2F से दूर रखी जाती है तो प्रतिबिंब लेंस के दूसरी तरफ F तथा 2F के मध्य बनता है। यह प्रतिबिंब वास्तविक, उल्टा तथा छोटे आकार का होता है।
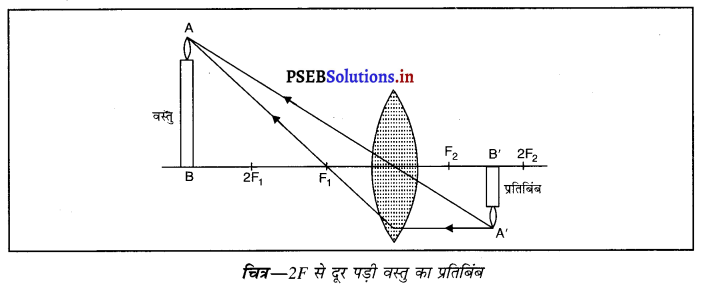
PSEB 10th Class Science Important Questions Chapter 10 प्रकाश-परावर्तन तथा अपवर्तन 9

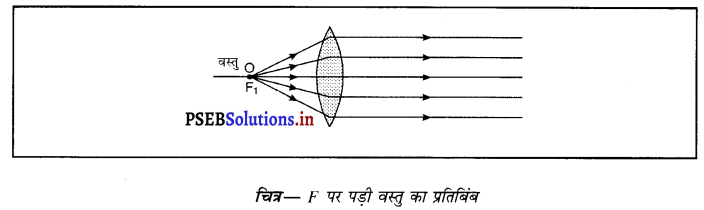
(iii) जब वस्तु F पर पड़ी हो-जब वस्तु उत्तल लेंस के F पर पड़ी हो तो प्रतिबिंब लेंस को दूसरी तरफ अनंत पर बनता है। यह प्रतिबिंब वास्तविक, उल्टा तथा आकार में बड़ा बनता है।
PSEB 10th Class Science Important Questions Chapter 10 प्रकाश-परावर्तन तथा अपवर्तन 10

प्रश्न 4.
चित्र में प्रकाश की कौन-सी क्रिया दर्शाई गई है ? इसकी परिभाषा दें तथा इसके नियम भी लिखो।
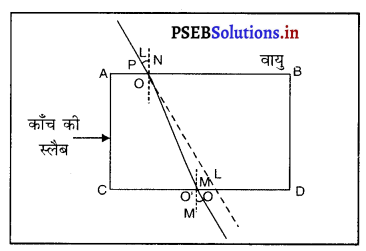
PSEB 10th Class Science Important Questions Chapter 10 प्रकाश-परावर्तन तथा अपवर्तन 11
उत्तर-
चित्र में प्रकाश अपवर्तन की क्रिया दर्शायी गई है।
प्रकाश का अपवर्तन—जब प्रकाश एक माध्यम से दूसरे माध्यम में प्रवेश करता है तो यह अपने पहले पथ से विचलित (मुड़) हो जाता है। प्रकाश के इस पथ परिवर्तन को प्रकाश का अपवर्तन कहते हैं। यदि प्रकाश किरण, प्रकाशीय विरल माध्यम से सघन माध्यम में प्रवेश करती है तो वह आपतन बिंदु पर बने अभिलंब की ओर मुड जाती है और यदि प्रकाश किरण सघन माध्यम से विरल माध्यम में प्रवेश करती है तो यह अभिलंब से दूर मुड़ जाती है।

प्रकाश अपवर्तन के नियम –
(i) आपतित किरण, अपवर्तित किरण और अभिलंब सदा एक ही तल में होते हैं।
(ii) जब एक प्रकाश-किरण किन्हीं दो माध्यमों के सीमा तल पर तिरछी आपतित होती है तो आपतन कोण (∠i) की ज्या (sine) तथा अपवर्तन कोण (∠r) की ज्या (sine) का अनुपात एक नियतांक होता है। इस नियतांक को दूसरे माध्यम का पहले माध्यम के सापेक्ष अपवर्तनांक कहते हैं। इसे 1_μ₂ से प्रकट करते हैं।
PSEB 10th Class Science Important Questions Chapter 10 प्रकाश-परावर्तन तथा अपवर्तन 12
प्रकाश के अपवर्तन के दूसरे नियम को स्नैल का नियम भी कहते हैं।

लघु उत्तरात्मक प्रश्न (Short Answer Type Questions)

प्रश्न 1.
प्रकाश क्या है ? इसकी प्रकृति क्या है ?
उत्तर-
(Light)-प्रकाश वह भौतिक साधन है जो हमें दूसरी वस्तुओं को देखने में सहायता करता है। प्रकाश स्वयं दिखाई नहीं देता। यह एक प्रकार की ऊर्जा है। प्रकाश वास्तव में विद्युत् चुंबकीय तरंगें हैं जो वायु अथवा निर्वात में एक स्थान से दूसरे स्थान तक सीधी रेखा में चलता है।

प्रश्न 2.
प्रकाश की प्रकृति की विशेषताएं लिखिए।
उत्तर-

इन्हें संचरण के लिए माध्यम की आवश्यकता नहीं होती।
यह विद्युत् चुंबकीय तरंगों के रूप में होता है।
इसकी चाल माध्यम की प्रकृति पर आधारित होती है।

प्रश्न 3.
प्रकाश के कृत्रिम स्रोत कौन-से हैं ? उदाहरण दें।
अथवा
मनुष्य द्वारा बनाए गए प्रकाश के स्त्रोत कौन-से हैं ? उदाहरण दें।
उत्तर-
प्रकाश के कृत्रिम स्त्रोत (Artificial Sources of Light) – प्रकाश के मुख्य कृत्रिम स्रोत-अग्नि, विद्युत्, गैस, दीप तथा कुछ रासायनिक क्रियाएं हैं।

प्रश्न 4.
परावर्तक क्या होता है ?
उत्तर-
परावर्तक (Reflector)- ऐसी चिकनी और चमकीली (पॉलिश की गई) सतह जो प्रकाश किरणों को उसी माध्यम में लौटा देती है जिससे वे किरणें आ रही होती हैं, को परावर्तक (Reflector) कहते हैं।

प्रश्न 5.
प्रकाश परावर्तन से क्या अभिप्राय है ? प्रकाश परावर्तन के नियम लिखो।
अथवा
प्रकाश का परावर्तन (Reflection of Light) क्या है ? प्रकाश के परावर्तन के नियम लिखें।
उत्तर-
प्रकाश का परावर्तन (Reflection of Light)-जब प्रकाश की किरणें किसी समतल और चमकदार सतह से टकराती हैं, तो विशेष दिशा में वापिस पहले माध्यम में ही लौट आती हैं। प्रकाश की इस प्रक्रिया को प्रकाश परावर्तन कहते हैं।

परावर्तन के नियम (Laws of Reflection)-

आपतन कोण (∠i) और परावर्तन कोण (∠r) एक-दूसरे के बराबर होते हैं।
अर्थात् ∠i = ∠r.
आपतित किरण परावर्तित किरण और आपतन बिंदु परावर्तित सतह आपतन बिंदु पर बना अभिलंब (normal) सभी दर्पण एक तल में होते हैं। चित्र में AB एक समतल परावर्तक सतह (दर्पण) है, PQ आपतित किरण, QR परावर्तित किरण और ON आपतन बिंदु पर अभिलंब हैं। चित्र से पता चलता है कि आपतित किरण, परावर्तित किरण तथा अभिलंब सभी कागज़ के तल में हैं।

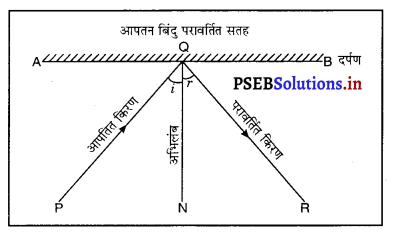
प्रश्न 6.
जब प्रकाश की कोई किरण दर्पण पर अभिलंब रूप में पड़ती है तो आपतन कोण कितना होता
उत्तर-
जब प्रकाश की कोई किरण दर्पण पर अभिलंब रूप में पड़ती है तो इस अवस्था में आपतन कोण शून्य अंश के बराबर होता है। (∠i = ∠0 °)

प्रश्न 7.
जब प्रकाश की किरण किसी दर्पण पर अभिलंब रूप में पड़ती है तो यह किस कोण पर परावर्तित होती है?
उत्तर-
जब प्रकाश की कोई किरण दर्पण पर अभिलंब रूप में पड़ती है (∠i = 0°) तो यह परावर्तित होकर अभिलंब की दिशा में वापिस मुड़ आती है। इस अवस्था में परावर्तित (∠r = 0° ) शून्य अंश का होता है।

प्रश्न 8.
किसी दर्पण पर अभिलंब रूप में पड़ रही किरण उसी पथ पर वापिस आ जाती है। क्यों ?
उत्तर–
किसी दर्पण पर अभिलंब रूप में पड़ रही किरण उसी पथ पर वापिस आ जाती है। इस अवस्था में आपतन कोण (∠i = 20°) शून्य है, क्योंकि परावर्तन के नियमानुसार आपतन कोण ∠i = परावर्तन कोण Lr होता है, इसलिए परावर्तन कोण भी (∠r = 0°) शून्य होगा तथा प्रकाश किरण उसी पथ पर लौट आएगी।

प्रश्न 9.
इन पदों की परिभाषा दो : गोलीय दर्पण, अवतल दर्पण, उत्तल दर्पण, द्वारक, वक्रता केंद्र, शीर्ष, मुख्य फोकस और फोकस-दूरी।
उत्तर-
(i) गोलीय दर्पण (Spherical Mirror) यदि दर्पण किसी खोखले गोले का भाग है जिसकी एक सतह पॉलिश की हुई हो और दूसरी सतह परावर्तक हो तो ऐसा दर्पण, गोलीय दर्पण कहलाता है।
गोलीय दर्पण दो प्रकार का होता है –

अवतल दर्पण तथा
उत्तल दर्पण

(ii) अवतल दर्पण (Concave Mirror)- एक ऐसा गोलीय दर्पण जिसकी परावर्तक सतह उस गोले के केंद्र की ओर होती है जिसका यह दर्पण एक भाग है, अवतल दर्पण कहलाता है। अवतल दर्पण की बाहरी मुख्य अक्ष सतह पॉलिश की हुई होती है तथा प्रकाश परावर्तन भीतरी सतह से होता है।
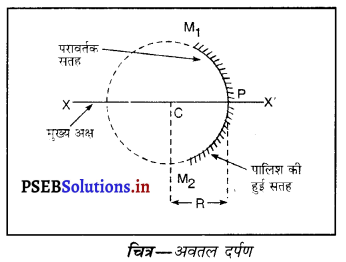
PSEB 10th Class Science Important Questions Chapter 10 प्रकाश-परावर्तन तथा अपवर्तन 14

(iii) उत्तल दर्पण (Convex Mirror)-एक ऐसा दर्पण जिसकी परावर्तक सतह उस गोले के केंद्र से परे (दूर) होती है जिस गोले का दर्पण एक भाग होता है, उत्तल दर्पण कहलाता है। उत्तल दर्पण की भीतरी सतह पॉलिश की हुई होती है तथा परावर्तन बाहरी सतह से होता है।
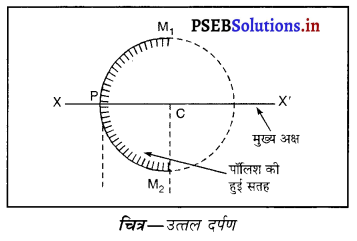
PSEB 10th Class Science Important Questions Chapter 10 प्रकाश-परावर्तन तथा अपवर्तन 15
(iv) द्वारक (Aperture)-दर्पण के उस भाग को, जिससे प्रकाश का परावर्तन होता है, दर्पण का द्वारक कहा जाता है। चित्र (a) और (b) में दूरी M₁ M₂ दर्पण का द्वारका कहलाता है।
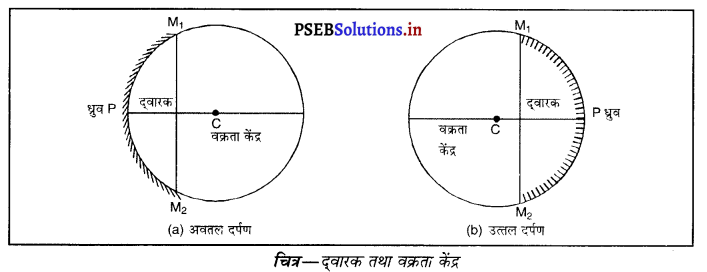
PSEB 10th Class Science Important Questions Chapter 10 प्रकाश-परावर्तन तथा अपवर्तन 16

(v) वक्रता-केंद्र (Centre of Curvature)-दर्पण का वक्रता केंद्र उस खोखले गोले का केंद्र है जिसका दर्पण एक भाग होता है। नीचे चित्र (a) में C एक अवतल दर्पण का वक्रता केंद्र है और चित्र (b) में C एक उत्तल दर्पण का वक्रता केंद्र है।

(vi) शीर्ष या ध्रुव (Pole)-गोलीय दर्पण के मध्य बिंदु या केंद्र को इसका ध्रुव या शीर्ष (vertex) कहा जाता है। नीचे चित्र (a) और (b) में इसे P से दर्शाया गया है।

(vii) मुख्य फोकस (Principal Focus)-दर्पण का मुख्य फोकस, मुख्य अक्ष पर वह बिंदु होता है जहाँ पर मुख्य अक्ष के समांतर आ रही प्रकाश किरणें दर्पण से परावर्तित होकर वास्तव में एक बिंदु पर आकर मिलें या इस बिंदु से अभिसरित होती हैं अथवा एक बिंदु से अपसरित होती हईं प्रतीत पडती हैं।
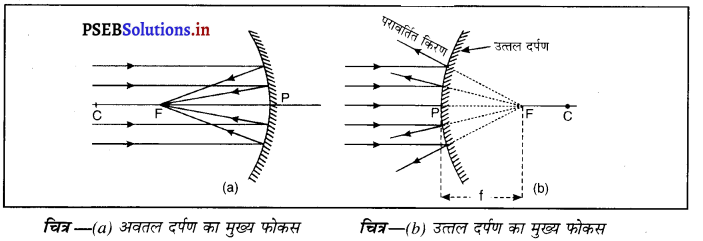
PSEB 10th Class Science Important Questions Chapter 10 प्रकाश-परावर्तन तथा अपवर्तन 17

(viii) फोकस दूरी (Focus Length)-गोलीय दर्पण के शीर्ष (ध्रुव) (P) और मुख्य फोकस (F) के मध्य की दूरी को दर्पण की फोकस दूरी कहा जाता है। इसे द्विारा प्रदर्शित किया जाता है। चित्र में PF फोकस दूरी है। एस० आई० पद्धति में फोकस दूरी का मात्रक (unit) मीटर हैं।

प्रश्न 10.
एक अवतल दर्पण की फोकस दूरी और वक्रता अर्धव्यास के मध्य क्या संबंध हैं ? समतल दर्पण की फोकस दूरी कितनी होती है ?
उत्तर-
एक अवतल दर्पण की फोकस दूरी उस दर्पण के वक्रता अर्धव्यास से आधी होती हैं। यदि अवतल दर्पण की फोकस दूरी f और वक्रता अर्धव्यास R हो, तो
f=\(\frac{1}{2}\) xR
समतल दर्पण की फोकस दूरी अनंत होती है।

प्रश्न 11.
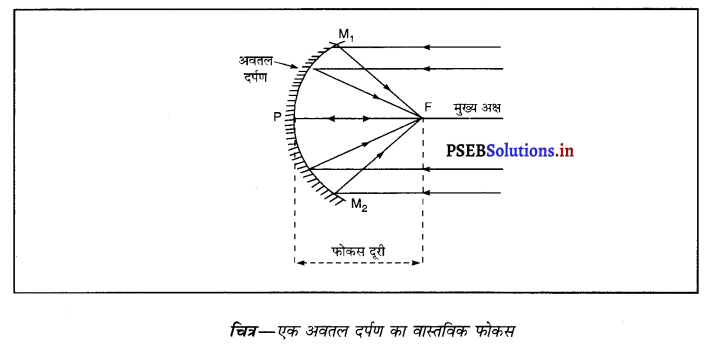
अवतल दर्पण का एक वास्तविक फोकस होता है। एक आरेख बनाकर इसकी व्याख्या करो।
उत्तर-
अवतल दर्पण का वास्तविक फोकस-क्योंकि अवतल दर्पण के मुख्य अक्ष के समांतर आ रही सभी किरणें दर्पण से परावर्तित होकर वास्तव में फोकस में से गुज़रती हैं, इसलिए अवतल दर्पण का फोकस वास्तविक होता है।
PSEB 10th Class Science Important Questions Chapter 10 प्रकाश-परावर्तन तथा अपवर्तन 18

प्रश्न 12.
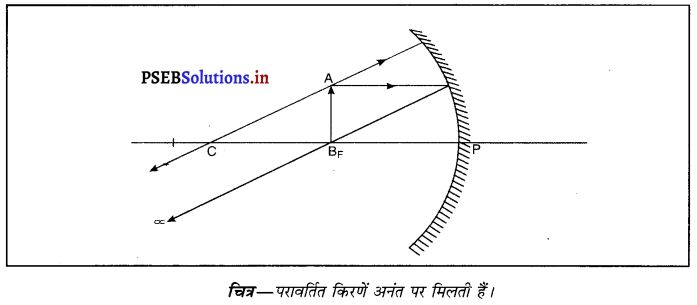
जब किसी अवतल दर्पण द्वारा बनाया गया प्रतिबिंब अनंत पर बनता है तो वस्तु कहाँ पर होती है ?
उत्तर-
जब वस्तु को अवतल दर्पण के फोकस पर रखा जाता है तो प्रतिबिंब अनंत पर बनता है तथा यह प्रतिबिंब वास्तविक तथा वस्तु की अपेक्षा आकार में बड़ा बनता है। इस अवस्था में वस्तु से आ रही प्रकाश किरणें परावर्तन के पश्चात् समांतर हो जाती हैं।
PSEB 10th Class Science Important Questions Chapter 10 प्रकाश-परावर्तन तथा अपवर्तन 19

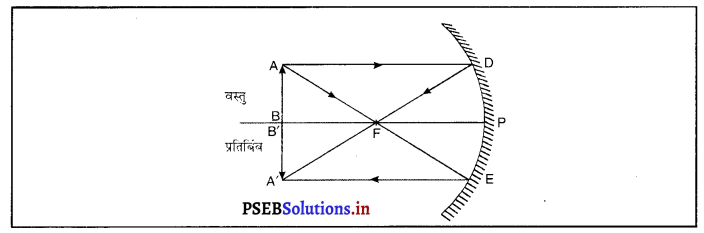
प्रश्न 13.
किसी वस्तु को एक अवतल दर्पण के सामने कहाँ पर रखा जाये ताकि इसका प्रतिबिंब वास्तविक और वस्तु के समान आकार का बने ?
उत्तर-
अवतल दर्पण द्वारा बना प्रतिबिंब वास्तविक तथा वस्तु के समान आकार का प्राप्त करने के लिए वस्तु को अवतल दर्पण के सामने वक्रता-केंद्र पर रखना चाहिए। इस अवस्था में प्रतिबिंब भी वक्रता-केंद्र पर बनेगा तथा यह वास्तविक, उल्टा और आकार में वस्तु के आकार के बराबर होगा।
PSEB 10th Class Science Important Questions Chapter 10 प्रकाश-परावर्तन तथा अपवर्तन 20

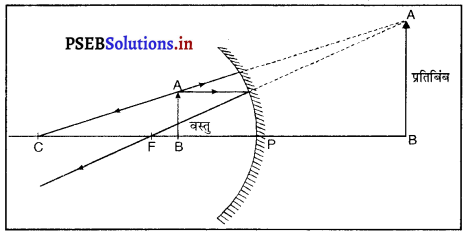
प्रश्न 14.
अवतल दर्पण में वस्तु का प्रतिबिंब बड़ा और आभासी कब बनता है ? आरेख दवारा दर्शाओ।
उत्तर-
जब वस्तु अवतल दर्पण के शीर्ष (Pole) और फोकस के मध्य रखी जाती है तो उस अवस्था में वस्तु प्रतिबिंब का प्रतिबिंब सीधा, आभासी तथा आकार में वस्तु की अपेक्षा बड़ा बनता है।
PSEB 10th Class Science Important Questions Chapter 10 प्रकाश-परावर्तन तथा अपवर्तन 21

प्रश्न 15.
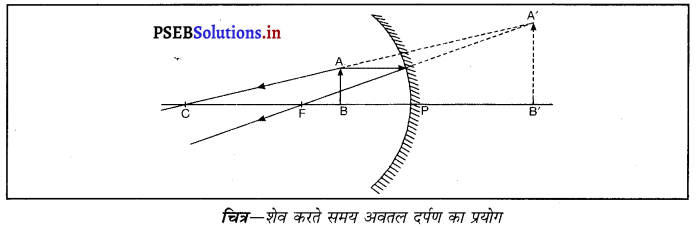
किसी दर्पण का उपयोग शेव करने के लिए किया जाता है और क्यों ? इसकी क्रिया को एक आरेख की सहायता से दर्शाओ।
उत्तर-
अवतल दर्पण का शेव करने वाले दर्पण के रूप में उपयोग किया जाता है क्योंकि जब हम अपना चेहरा किसी अवतल दर्पण के निकट (शीर्ष और फोकस के मध्य) रखते हैं तो चेहरे का प्रतिबिंब आकार में बड़ा और सीधा बनता है, जिससे बारीक बाल भी दिखाई देते हैं, अर्थात् यह चेहरे की ठीक शेव (Shave) करने में सहायक होता है। इसलिए अवतल दर्पण को शेव करने वाले दर्पण के रूप में प्रयोग किया जाता है ।
PSEB 10th Class Science Important Questions Chapter 10 प्रकाश-परावर्तन तथा अपवर्तन 22

प्रश्न 16.
कौन-सा दर्पण हमेशा आभासी, सीधा और वस्तु से छोटे आकार का प्रतिबिंब बनाता है ?
उत्तर-
उत्तल दर्पण के लिए वस्तु की स्थिति यद्यपि कोई भी हो, प्रतिबिंब सदा आभासी, सीधा, उत्तल दर्पण वस्तु से छोटा और दर्पण के पीछे बनेगा।
PSEB 10th Class Science Important Questions Chapter 10 प्रकाश-परावर्तन तथा अपवर्तन 23

प्रश्न 17.
किस दर्पण की दृष्टि क्षेत्र बड़ा होता है ?
उत्तर-
उत्तल दर्पण में प्रतिबिंब सदा आभासी सीधा तथा वस्तु से छोटे आकार का और दर्पण के पीछे बनता है। दर्पण को वस्तु से दूर ले जाने पर पीछे की ओर के बड़े क्षेत्र में पड़ी वस्तुएं देखी जा सकती हैं। इस प्रकार इसका दृष्टि क्षेत्र बड़ा हो जाता है। अतः उत्तल दर्पण का दृष्टि क्षेत्र बड़ा होता है।

प्रश्न 18.
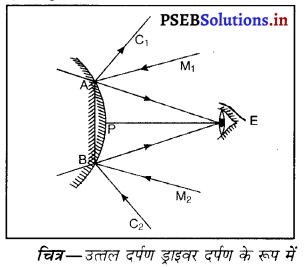
किस दर्पण को ड्राइवर के दर्पण के रूप में पहल दी जाती है और क्यों ? आरेख बनाकर दर्शाओ।
उत्तर-
उत्तल दर्पण को ड्राइवर के दर्पण के रूप में पहल दी जाती है क्योंकि उत्तल दर्पण में बन रहा प्रतिबिंब वस्तु से बहुत छोटा तथा सीधा बनता है। इसलिए उत्तल दर्पण द्वारा पीछे आ रही ट्रैफिक का एक बड़ा भाग दिखाई देता है।
PSEB 10th Class Science Important Questions Chapter 10 प्रकाश-परावर्तन तथा अपवर्तन 24

प्रश्न 19.
पीछे की ट्रैफिक देखने के लिए वाहनों में किस प्रकार के दर्पण का प्रयोग किया जाता है ?
उत्तर-
क्योंकि उत्तल दर्पण में पीछे आ रही ट्रैफिक का सीधा तथा छोटा प्रतिबिंब बनता है, इसलिए बड़े क्षेत्र में आ रहे वाहनों को देखने के लिए उत्तल दर्पण का प्रयोग वाहनों के दर्पण के रूप में किया जाता है ।

प्रश्न 20.
समतल दर्पण, अवतल दर्पण और उत्तल दर्पण को बिना छुए आप इनमें अंतर कैसे मालूम करोगे ?
उत्तर-
दर्पणों की पहचान करना प्रतिबिंब देखकर–प्रत्येक दर्पण में अपने चेहरे का प्रतिबिंब देखें। अब अपना चेहरा दर्पण से दूर ले जाओ और प्रतिबिंब का आकार नोट करो। आप देखेंगे कि समतल दर्पण में बन रहे प्रतिबिंब का आकार चेहरे के आकार के बराबर तथा अवतल दर्पण में बड़ा और उत्तल दर्पण में प्रतिबिंब का आकार छोटा होगा। इस तरह हम बिना छुए समतल दर्पण, अवतल दर्पण और उत्तल दर्पण में पहचान कर सकते हैं।

प्रश्न 21.
एक गोलीय दर्पण के आवर्धन की परिभाषा दो। समतल दर्पण में आवर्धन कितना होता है?
अथवा
आवर्धन (Magnification) किसे कहते हैं ?
उत्तर-
आवर्धन (Magnification)-गोलीय दर्पण का आवर्धन दर्पण द्वारा बनाये गए प्रतिबिंब के आकार या ऊँचाई (Size) और वस्तु के आकार या ऊँचाई (Size) के अनुपात के बराबर होता है। इसे m द्वारा प्रदर्शित किया जाता है।
PSEB 10th Class Science Important Questions Chapter 10 प्रकाश-परावर्तन तथा अपवर्तन 25
समतल दर्पण का आवर्धन-समतल दर्पण को एक ऐसे गोले का भाग माना जा सकता है जिसका अर्धव्यास अनंत है।
∴ दर्पण फार्मूला लगाकर \(\frac{1}{u}+\frac{1}{v}=\frac{1}{f}\)
\(\frac{1}{u}+\frac{1}{v}=\frac{1}{\infty}\)
\(\frac{1}{u}+\frac{1}{v}=0\)
u+v = 0
u = -v
अब आवर्धन (m) = \(\frac{-v}{u}=\frac{u}{u} \) = 1
अर्थात् वस्तु का आकार और प्रतिबिंब का आकार एक समान होते हैं।

प्रश्न 22.
एक समतल दर्पण के द्वारा बनाये गए प्रतिबिंब के लक्षण लिखो।
उत्तर-
समलत दर्पण में बने प्रतिबिंब के लक्षण (गुण)-

यह आभासी होता है, अर्थात् इसे पर्दे पर प्राप्त नहीं किया जा सकता।
यह सीधा होता है।
इसमें पार्श्व परावर्तन होता है, अर्थात् दायाँ हाथ दर्पण में बायाँ दिखाई देता है और बायाँ हाथ दायाँ दिखाई देता है।
समतल दर्पण में बने प्रतिबिंब आकार वस्तु के आकार के बराबर होता है।
प्रतिबिंब दर्पण के पीछे उतनी ही दूरी पर बनता है जितनी दूरी पर वस्तु दर्पण के सामने रखी जाती है।

प्रश्न 23.
प्रतिबिंब से क्या तात्पर्य है ? आभासी तथा वास्तविक प्रतिबिंब में क्या अंतर है ?
उत्तर-
प्रतिबिंब-दर्पण के सामने रखी वस्तु की दर्पण में जो आकृति बन जाती है उस आकृति को वस्तु का प्रतिबिंब कहते हैं। प्रतिबिंब की परिभाषा निम्नलिखित प्रकार से दी जाती है – “जब प्रकाश की किरणें किसी बिंदु से चलकर परावर्तन के पश्चात् (दर्पण में) अथवा अपवर्तन के पश्चात् (लेंस में) किसी दूसरे बिंदु पर जाकर मिलती है अथवा दूसरी बिंदु से आती हुई प्रतीत होती हैं तो इस दूसरे बिंदु को पहले बिंदु का प्रतिबिंब कहते हैं।”

वास्तविक तथा आभासी प्रतिबिंब में अंतर

एक वास्तविक प्रतिबिंब (Real Image)	आभासी प्रतिबिंब (Virtual Image)
(1) परावर्तन या अपवर्तन के बाद यदि प्रकाश की किरणें परस्पर मिलें तो प्रतिबिंब वास्तविक बनता है।	(1) परावर्तन या अपवर्तन के बाद यदि प्रकाश की किरणें परस्पर न मिलें (पीछे को बढ़ाकर उन्हें मिलना पड़े) तो प्रतिबिंब आभासी बनता है।
(2) यह प्रतिबिंब पर्दे पर प्राप्त किया जा सकता है।	(2) यह प्रतिबिंब पर्दे पर प्राप्त नहीं किया जा सकता है।
(3) यह प्रतिबिंब हमेशा उल्टा बनता है।	(3) यह प्रतिबिंब सीधा बनता है।

प्रश्न 24.
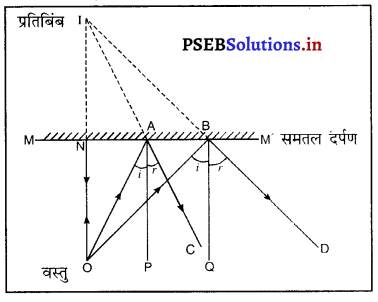
समतल दर्पण द्वारा प्रतिबिंब की रचना चित्र सहित समझाएं।
अथवा
कैसे दर्शाओगे कि समतल दर्पण में बने प्रतिबिंब की दर्पण से दूरी उसके सामने पड़ी वस्तु की दर्पण से दूरी के बराबर होती है।
उत्तर-
समतल दर्पण द्वारा प्रतिबिंब की लिमिट रचना-मान लो MM’ एक समतल दर्पण है और उसके सामने वस्तु 0 पड़ी है। OA और OB दो आपाती किरणें निकल रही हैं। AC और BD इनकी अनुसारी परावर्तित किरणें हैं, I प्रतिबिंब है। क्योंकि परावर्तित किरणें वास्तव में I पर नहीं मिलती | M aiyammiliauranizarrILM’ समतल दर्पण परंतु I पर मिलती हुई दिखाई देती हैं, इसलिए । वस्तु 0 का आभासी प्रतिबिंब है। मापने से पता चलता है कि NO = NI अर्थात् प्रतिबिंब दर्पण के पीछे उतनी दूरी पर बनता है जितनी दूरी पर दर्पण के सामने रखी रहती है।
PSEB 10th Class Science Important Questions Chapter 10 प्रकाश-परावर्तन तथा अपवर्तन 26

प्रश्न 25.
गोलीय दर्पण के मुख्य उपयोग लिखो।
उत्तर-
गोलीय दर्पण के उपयोग-गोलीय दर्पण दो प्रकार के होते हैं।
(1) अवतल दर्पण
(2) उत्तल दर्पण।

(1) अवतल दर्पण के उपयोग–

अवतल दर्पण, परावर्तक के रूप में प्रयोग में लाया जाता है। बड़े व्यास वाले दर्पणों को परावर्तक दूरदर्शी में प्रयुक्त किया जाता है।
एक अवतल दर्पण जिसके केंद्र में सुराख होता है, डॉक्टर के सिर के दर्पण (head mirror) के रूप में आँख, नाक, गले तथा कान के निरीक्षण के लिए प्रयोग में लाया जाता है।
जब वस्तु को दर्पण के शीर्ष तथा फोकस के मध्य रखा जाता है तो यह सीधा, बड़ा तथा आभासी प्रतिबिंब बनाता है। इसलिए इसे शेव दर्पण के रूप में प्रयोग में लाया जाता है।
अवतल दर्पण कार की लैंप तथा सर्चलाइट में प्रयुक्त किया जाता है।

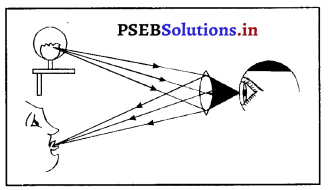
PSEB 10th Class Science Important Questions Chapter 10 प्रकाश-परावर्तन तथा अपवर्तन 27

(2) उत्तल दर्पण के उपयोग-
उत्तल दर्पण, ड्राइवरों द्वारा पीछे आ रहे ट्रैफिक का अधिक दृष्टि क्षेत्र में देखने के लिए प्रयोग किया जाता है क्योंकि इस दर्पण में प्रतिबिंब छोटा, सीधा तथा आभासी होता है।
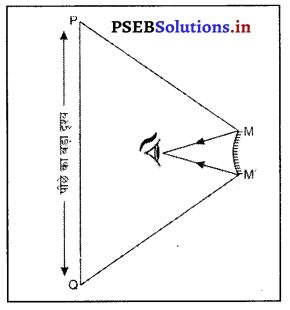
PSEB 10th Class Science Important Questions Chapter 10 प्रकाश-परावर्तन तथा अपवर्तन 28

प्रश्न 26.
उत्तल दर्पण द्वारा बनाए गए प्रतिबिंब की रचना आरेख चित्र द्वारा समझाओ।
अथवा
किसी अवतल दर्पण द्वारा बिंब के प्रतिबिंब बनने का स्थान निर्धारित करने के लिए न्यूनतम कितनी किरणों की आवश्यकता होती है ? एक अवतल दर्पण द्वारा आभासी प्रतिबिंब का बनना एक किरण आरेख खींचकर दिखाइए।
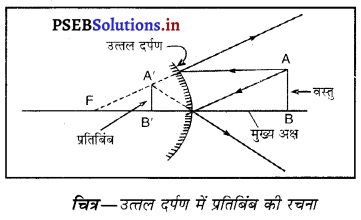
उत्तर-
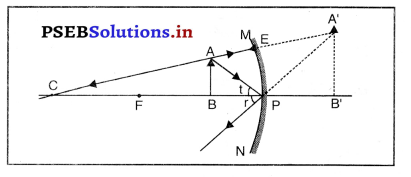
किसी अवतल दर्पण द्वारा बिंब के प्रतिबिंब बनने का स्थान निर्धारित करने के लिए न्यूनतम दो किरणों की आवश्यकता होती है। अवतल दर्पण द्वारा आभासी प्रतिबिंब की रचनाउत्तल दर्पण द्वारा बनाए गए प्रतिबिंब की रचना (Formation of Image by Convex Mirror)-मान लो एक वस्तु AB उत्तल दर्पण के सामने इसके मुख्य अक्ष पर पड़ी है। एक किरण AD, A बिंदु से चलकर दर्पण से
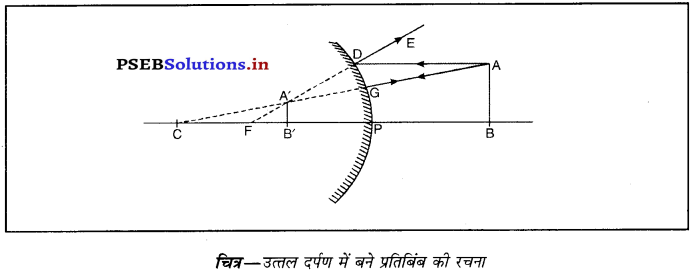
PSEB 10th Class Science Important Questions Chapter 10 प्रकाश-परावर्तन तथा अपवर्तन 29
परावर्तन के पश्चात् DE दिशा में जाती है जोकि मुख्य फोकस F में से आ रही दिखाई पड़ती है। एक अन्य आपतित किरण AC, वक्रता केंद्र C से परावर्तित होकर, वापिस मुड़ जाती है। ये दोनों परावर्तित किरणे A’ पर मिलती हुई दिखाई दोती हैं जो A का आभासी प्रतिबिंब हैं। A’ पर बना लंब A B’ वस्तु AB का आभासी, सीधा तथा आकार में छोटा प्रतिबिंब है।

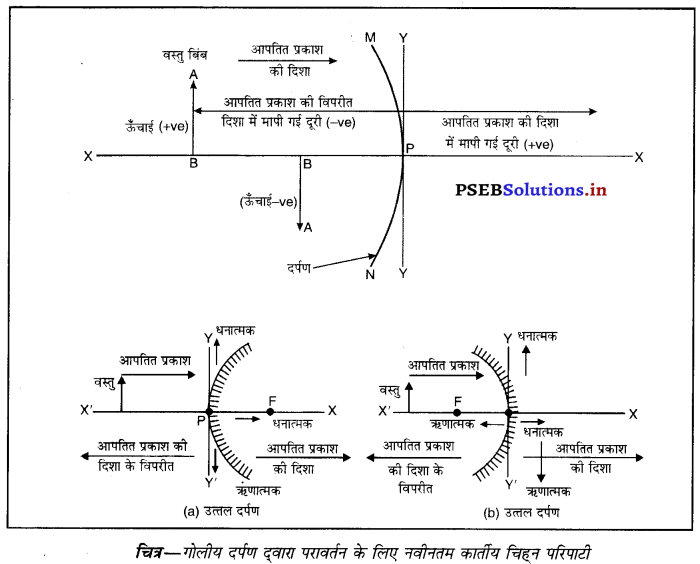
प्रश्न 27.
गोलीय दर्पणों के लिए नई कार्तीय चिह्न परंपराओं की चर्चा करो।
अथवा
गोलीय दर्पणों द्वारा परावर्तन के लिए कौन-सी चिह्न परिपाटी का प्रयोग किया जाता है ?
उत्तर-
नई कार्तीय चिह्न प्रतिबिंब परंपराएं (New Cartesian Sign Conventions)

वस्तु (या बिंब) दर्पण से बायीं ओर होता है तथा वस्तु से चलने वाली आपतित किरणें बायीं ओर से दायीं ओर जाती हुई मानी गई हैं।
सभी दूरियां गोलीय दर्पण के शीर्ष (Pole) से मापी जाती हैं।
आपतित प्रकाश की दिशा में मापी जाने वाली दूरियों को धनात्मक और आपतित प्रकाश की दिशा से विपरीत दिशा में मापी जाने वाली दूरियों को ऋणात्मक माना जाता है।
दर्पणों के मुख्य अक्ष के समकोणीय ऊपर की ओर मापी जाने वाली ऊँचाइयों को धनात्मक और इसके विपरीत नीचे की ओर ऊँचाइयों को ऋणात्मक माना जाता है।

PSEB 10th Class Science Important Questions Chapter 10 प्रकाश-परावर्तन तथा अपवर्तन 30

प्रश्न 28.
प्रकाश की एक किरण समतल दर्पण के साथ 40° का कोण बनाती है। इसका परावर्तन कोण कितना होगा ?
उत्तर-
प्रकाश की किरण का समतल दर्पण के साथ बना कोण = 40°
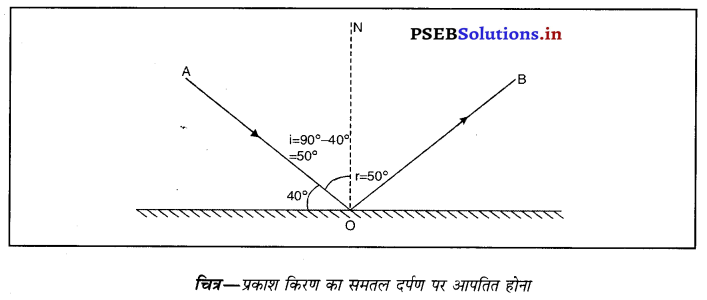
PSEB 10th Class Science Important Questions Chapter 10 प्रकाश-परावर्तन तथा अपवर्तन 31
∴ अभिलंब आपतित तथा किरण के मध्य साथ बना कोण = ∠i = 90° – 40° = 50° ‘
∵ ∠i = ∠r
अत : r = 50°

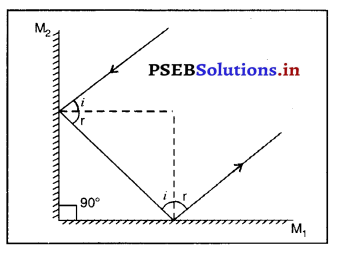
प्रश्न 29.
दो समतल दर्पणों को किस प्रकार : व्यवस्थित किया जाए कि परावर्तित किरण के समानांतर हैं ?
उत्तर-
परावर्तित किरण सदैव आपतित किरण के समानांतर होगी यदि दो समतल दर्पण एक-दूसरे के लंबवत् व्यवस्थित किए जाएं जैसा कि चित्र में दर्शाया गया है।
PSEB 10th Class Science Important Questions Chapter 10 प्रकाश-परावर्तन तथा अपवर्तन 32

प्रश्न 30.
विसरित परावर्तन (Diffused Reflection) से क्या तात्पर्य है?
उत्तर-
समानांतर किरणें किसी ऐसे तल से टकराती हैं जो असमतल (खुरदरा) हो तो प्रकाश की परावर्तित किरणों का एक बड़ा भाग टकराने के बाद अनियमित रूप से फैल जाता है, तो ऐसे परावर्तन को विसरित परावर्तन कहते हैं।
उदाहरण-पुस्तक के अक्षरों अथवा ब्लैक बोर्ड पर लिखे गए शब्दों का पढ़ जाना विसरित परावर्तन के विसतरित परावर्तन कारण ही संभव है।
PSEB 10th Class Science Important Questions Chapter 10 प्रकाश-परावर्तन तथा अपवर्तन 33

प्रश्न 31.
प्रकाशीय माध्यम किसे कहते हैं ? ये कितने प्रकार के होते हैं ?
उत्तर-
प्रकाशीय माध्यम-जिस भौतिक साधन में से प्रकाश सुगमता से गुज़र सकता है, उसे प्रकाशीय माध्यम कहते हैं; जैसे वायु, पानी, काँच आदि।
माध्यम निम्नलिखित तीन प्रकार के होते हैं

पारदर्शी माध्यम-वह माध्यम जिसमें से प्रकाश की किरणें सुगमता से गुज़र सके और उसके दूसरी ओर पड़ी हुई वस्तुएं स्पष्ट दिखाई दें, पारदर्शी माध्यम कहलाता है; जैसे साफ पानी, काँच आदि।
अपारदर्शी माध्यम-जिस माध्यम में से प्रकाश की किरणें न गुज़र सकें और दूसरी ओर पड़ी हुई वस्तुएं दिखाई न दें, अपारदर्शी माध्यम कहलाता है ; जैसे ईंट, गत्ता, लोहे की चादर आदि।
पारभासी माध्यम-जिस माध्यम में से प्रकाश किरणे अल्प मात्रा में गुज़रे और दूसरी तरफ पड़ी हुई वस्तुएं धुंधली दिखाई दें, पारभासी माध्यम कहलाता है, जैसे धुंधला काँच, तेल लगा कागज़।

प्रश्न 32.
घनत्व की दृष्टि से माध्यम कितने प्रकार के होते हैं ?
उत्तर-
घनत्व की दृष्टि से माध्यम दो प्रकार के होते हैं –

विरल माध्यम-कम घनत्व वाले माध्यम को विरल माध्यम कहते हैं। उदाहरण-वायु।
सघन माध्यम-अधिक घनत्व वाले माध्यम को सघन माध्यम कहते हैं। उदाहरण-काँच।

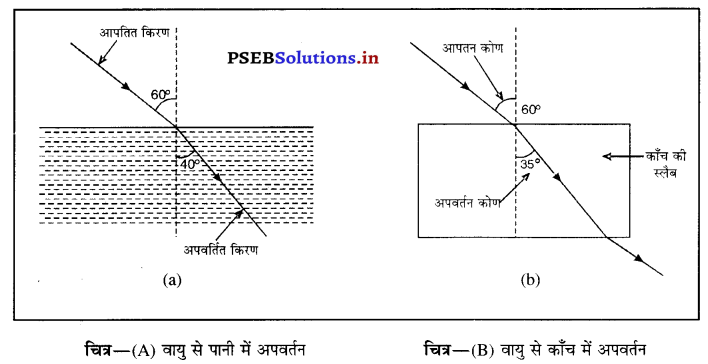
प्रश्न 33.
विरल माध्यम से सघन माध्यम में प्रवेश करते हुए माध्यम की अधिक सघनता का प्रकाश किरण पर क्या प्रभाव पड़ता है ? सचित्र उदाहरण से इसे समझाइए ।
अथवा
अपवर्तन में माध्यम की सघनता का अपवर्तित किरण के झुकाव पर क्या प्रभाव पड़ता है ? चित्र द्वारा समझाइए।
उत्तर-
जब प्रकाश की किरण विरल से सघन माध्यम में प्रवेश करती है तो यह अभिलंब की ओर मुड़ जाती है। माध्यम जितना अधिक सघन होगा, किरण उतनी ही अधिक अभिलंब की ओर मुड़ेगी। आगे दिए गए चित्र में प्रकाश की किरण वायु से पानी में तथा वायु से कांच में प्रवेश करती दिखाई गई है। किरण का झुकाव पानी की अपेक्षा काँच में अधिक है क्योंकि काँच पानी की अपेक्षा अधिक सघन है।
PSEB 10th Class Science Important Questions Chapter 10 प्रकाश-परावर्तन तथा अपवर्तन 34

प्रश्न 34.
जल से काँच में प्रवेश करने पर प्रकाश की चाल में क्या परिवर्तन होता है ?
उत्तर–
जल, काँच की अपेक्षा विरल माध्यम है। इसलिए प्रकाश जब जल से काँच में प्रवेश करता है तो प्रकाश की चाल कम हो जाती है तथा प्रकाश अभिलंब की ओर मुड़ जाता है। इस अवस्था में आपतन कोण (i) अपवर्तन कोण (r) से बड़ा होता है।

प्रश्न 35.
यदि प्रकाश की किरण काँच से जल में प्रवेश करें तो प्रकाश की किरणें अभिलंब की ओर मुड़ेंगी या अभिलंब से दूर हटेंगी ?
उत्तर-
इस अवस्था में प्रकाश सघन माध्यम (काँच) से जल (विरल माध्यम) में प्रवेश कर रही हैं जिससे अपवर्तन होने पर अभिलंब से दूर हटेंगी। इस अवस्था में आपतन कोण (i) अपवर्तन कोण (r) से कम होगा तथा जल में प्रकाश की चाल अधिक हो जायेगी।

प्रश्न 36.
वास्तविक और आभासी गहराई के संदर्भ में अपवर्तनांक ज्ञात करो।
उत्तर-
यह सामान्य ज्ञान है कि पानी की तालाब में गहराई अधिक प्रतीत होती है। उसका तल कुछ ऊपर उठा हुआ प्रतीत होता है। मान लो एक वस्तु तालाब की गहराई में A पर है। एक किरण AB तल से टकरा कर सामान्यत: BD की ओर अपवर्तित हो जाती है। A से एक अन्य किरण C पर आपतन Zi बना कर अभिलंब की ओर मुड़ जाती है। CE अपवर्तन Lr बनाती है और आँख तक पहुंचती है। इससे A अपने स्थान पर न रह कर A’ पर प्रतीत होता है।
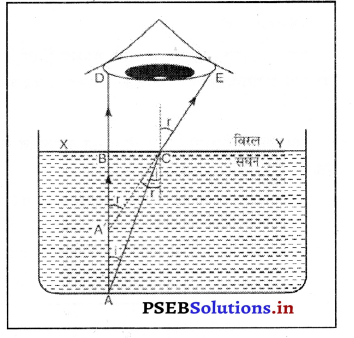
PSEB 10th Class Science Important Questions Chapter 10 प्रकाश-परावर्तन तथा अपवर्तन 35
a_b_ω = \(\frac{1}{a_{b_{a}}}=\frac{1}{u}\)
\(\frac{\sin i}{\sin r}=a_{b_{\omega}}=\frac{1}{u}\)
\(\frac{\mathrm{BC} / \mathrm{AC}}{\mathrm{BC} / \mathrm{A}^{\prime} \mathrm{C}}=\frac{1}{\mu} \)

या µ = \(\frac{\mathrm{AC}}{\mathrm{A}^{\prime} \mathrm{C}}\)
क्योंकि B और C बहुत निकट हैं
∴ AC लगभग AB और A’C लगभग A’B के बराबर है।
PSEB 10th Class Science Important Questions Chapter 10 प्रकाश-परावर्तन तथा अपवर्तन 36

प्रश्न 37.
पानी में डूबी हुई लकड़ी मुड़ी हुई प्रतीत होती है। क्यों ?
उत्तर-
पानी में आंशिक रूप से एक सीधा लकड़ी का टुकडा (या पेंसिल) मुड़ा हुआ प्रतीत होता है। मान लो पानी में लकड़ी का एक सीधा टुकड़ा डुबोया गया है जो प्रकाश के अपवर्तन के कारण मुड़ा हुआ प्रतीत होगा। जैसे ही प्रकाश की किरणें बिंदु A से सघन माध्यम से विरल माध्यम में आती हैं तो वह लंब से परे मुड़ जाती हैं इस प्रकार बिंदु A बिंदु A के रूप में दिखाई देता है जिस कारण लकड़ी का टुकड़ा मुड़ा हुआ लगता है।
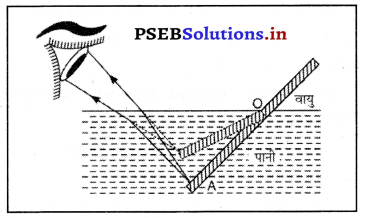
PSEB 10th Class Science Important Questions Chapter 10 प्रकाश-परावर्तन तथा अपवर्तन 37
इस प्रकार AO भाग A’ के रूप में दिखाई देता है तथा लकड़ी का टुकड़ा टेढ़ा प्रतीत होता है।

प्रश्न 38.
क्या कारण है कि पानी से भरे टब में तल पर रखा सिक्का हमें ऊँचा उठा हुआ प्रतीत होता है ? चिन द्वारा दर्शाओ कि प्रकाश किरणें कैसे चलती हैं ?
उत्तर-
सिक्के का पानी में ऊपर उठा हुआ प्रतीत होना- इसका कारण प्रकाश का अपवर्तन है। जब प्रकाश की किरण सघन माध्यम से चलकर विरल माध्यम में प्रवेश करती है, तो अभिलंब से दूर हट जाती है जिसके कारण बाहर से देखने पर हमें सिक्का ऊपर उठा दिखाई देता है।
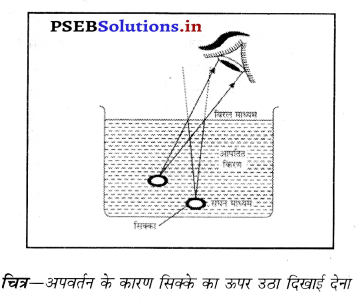
PSEB 10th Class Science Important Questions Chapter 10 प्रकाश-परावर्तन तथा अपवर्तन 38

प्रश्न 39.
स्नेल के नियम की परिभाषा दो ।
उत्तर-
स्नेल का नियम (Snell’s Law)-अपवर्तन के दूसरे नियम को स्नेल का नियम कहते हैं। इस नियम के अनुसार आपतन कोण के साइन (sine i) अर्थात् (sin (i) और अपवर्तन कोण के साइन (sine r) अर्थात (sin r) का अनुपात (ratio) स्थिरांक होता है।
∴ \(\frac{\sin i}{\sin r} \) = स्थिरक = a_µ_b

प्रश्न 40.
अपवर्तनांक किसे कहते हैं ? इसका संख्यात्मक सूत्र भी लिखें।
उत्तर-
अपवर्तनांक (Refractive Index)-निर्वात में प्रकाश के वेग और किसी अन्य माध्यम में प्रकाश के वेग के अनुपात को उस माध्यम का निरपेक्ष अपवर्तनांक कहते हैं।
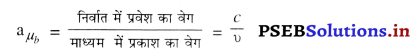
PSEB 10th Class Science Important Questions Chapter 10 प्रकाश-परावर्तन तथा अपवर्तन 39
a_µ_b को माध्यम b का माध्यम a के सापेक्ष अपवर्तनांक कहते हैं अर्थात् प्रकाश माध्यम a से माध्यम b में प्रवेश करता है। अपवर्तनांक की कोई इकाई नहीं होती, क्योंकि यह दो एक जैसी राशियों का अनुपात है।

प्रश्न 41.
लेंस की परिभाषा दो। भिन्न-भिन्न प्रकार के लेंस कौन-से हैं ?
उत्तर-
लेंस (Lens)- यह एक पारदर्शी अपवर्तन करने वाले माध्यम का भाग है जो दो गोलीय पृष्ठों या एक गोलीय पृष्ठ तथा दूसरा समतल पृष्ठ से घिरा होता है। लेंस दो प्रकार के होते हैं-

उत्तल लेंस
अवतल लेंस।

PSEB 10th Class Science Important Questions Chapter 10 प्रकाश-परावर्तन तथा अपवर्तन 40

प्रश्न 42.
पद (1) प्रकाशिक केंद्र (2) मुख्य अक्ष (3) मुख्य फोकस का परिभाषा दो।
उत्तर-
1. प्रकाशिक केंद्र (Optical Centre)-लेंस के मध्य बिंदु को प्रकाशिक केंद्र कहा जाता है।
PSEB 10th Class Science Important Questions Chapter 10 प्रकाश-परावर्तन तथा अपवर्तन 41
चित्र-अवतल लेंस चित्र (a) में C उत्तल लेंस का प्रकाशिक केंद्र है तथा चित्र (b) में C अवतल लेंस का प्रकाशिक केंद्र है। इस बिंदु में से गुजरने वाली प्रकाश किरण मुड़ती (विचलित) नहीं है।

2. मुख्य अक्ष (Principal Axis)- किसी लेंस का मुख्य अक्ष वह काल्पनिक रेखा है जो कि इसके प्रकाशिक केंद्र में से गुज़रती है और यह लेंस के दोनों गोलीय पृष्ठों पर अभिलंब होता है। चित्र (a) में EF उत्तल लेंस का तथा चित्र (b) में चित्र EF अवतल लेंस का मुख्य अक्ष हैं।
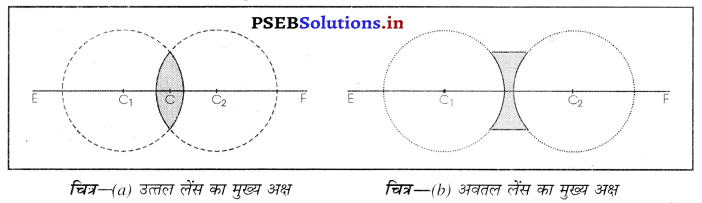
PSEB 10th Class Science Important Questions Chapter 10 प्रकाश-परावर्तन तथा अपवर्तन 42

3. मुख्य फोकस (Principal Focus)-यह लेंस के मुख्य अक्ष पर वह बिंदु हैं जिस पर मुख्य अक्ष के समांतर आ रही प्रकाश किरणे अपवर्तन के पश्चात् रूप में मिलती हैं (उत्तल लेंस) या (अवतल लेंस) पीछे की तरफ बढ़ाने पर मिलती हुई प्रतीत होती हैं।
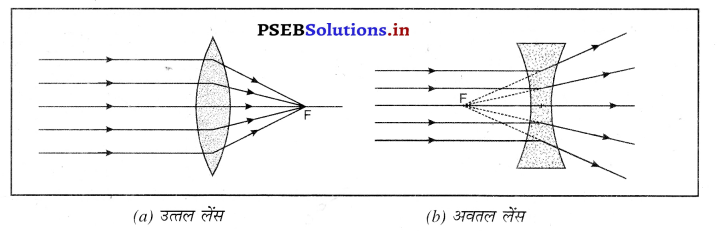
PSEB 10th Class Science Important Questions Chapter 10 प्रकाश-परावर्तन तथा अपवर्तन 43

प्रश्न 43.
उत्तल लेंस से अपवर्तन द्वारा प्रतिबिंब बनाने के लिए कौन-कौन से नियम हैं ?
उत्तर-
लेंस से अवपर्तन द्वारा प्रतिबिंब बनाने के लिए नियम (Rules for Image Formation after refraction through lens)-(i) मुख्य अक्ष के समांतर प्रकाश की किरण अपवर्तन के बाद मुख्य फोकस से गुज़रती है।
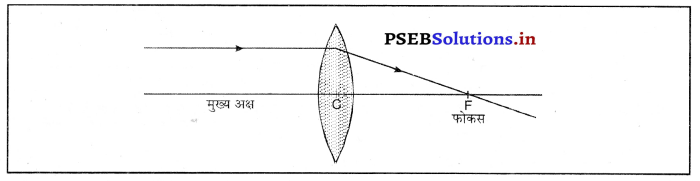
PSEB 10th Class Science Important Questions Chapter 10 प्रकाश-परावर्तन तथा अपवर्तन 44
(ii) मुख्य फोकस में से गुज़र रही प्रकाश की किरण अपवर्तन के बाद मुख्य अक्ष के समांतर हो जाती है।
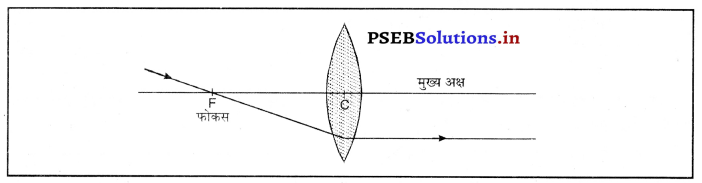
PSEB 10th Class Science Important Questions Chapter 10 प्रकाश-परावर्तन तथा अपवर्तन 45
(iii) लेंस के प्रकाशिक केंद्र में से गुजर रही प्रकाश किरण विचलित नहीं होती।
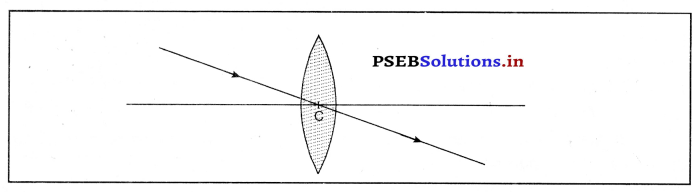
PSEB 10th Class Science Important Questions Chapter 10 प्रकाश-परावर्तन तथा अपवर्तन 46

प्रश्न 44.
किसी अवतल लेंस द्वारा प्रतिबिंब कैसे बनता है ? किरण आरेख खींच कर दिखाएं प्रतिबिंब की स्थिति तथा प्रकृति कैसी होगी ?
उत्तर-
अवतल लेंस के सामने रखी किसी वस्तु के प्रतिबिंब का किरण आरेख चित्र में दिखाया गया है, अवतल लेंस द्वारा बनाया गया प्रतिबिंब सदैव लेंस के प्रकाशित केंद्र तथा फोकस के बीच वस्तु की ओर ही बनता है। यह प्रतिबिंब सदैव आकार में छोटा, सीधा तथा आभासी होता है।
PSEB 10th Class Science Important Questions Chapter 10 प्रकाश-परावर्तन तथा अपवर्तन 47

प्रश्न 45.
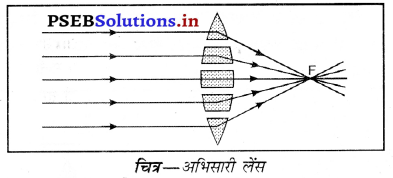
चित्र की सहायता से समझाइए कि उत्तल लेंस को अभिसारी लेंस क्यों कहा जाता है ?
उत्तर-
उत्तल लेंस की प्रिज़्मों के समूह से निर्मित हुआ माना जाता है, जैसा कि चित्र में दर्शाया गया है। क्योंकि प्रिज्म में से गुजरने वाली किरण इसके आधार की ओर मुड़ जाती है, इसलिए यह संयोजन प्रकाश को अभिसरित करने की क्षमता रखता है। अतः इसे अभिसारी लेंस कहते है।
PSEB 10th Class Science Important Questions Chapter 10 प्रकाश-परावर्तन तथा अपवर्तन 48

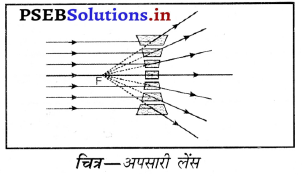
प्रश्न 46.
चित्र की सहायता से समझाइए कि अवतल लेंस को अपसारी लेंस क्यों कहा जाता है?
उत्तर-
अवतल लेंस के दो प्रिज्मों को जिनके शीर्षक कांच पट्टिका की आमने-सामने वाली फलकों से संपर्क किए हुए हों, के समान माना जाता है। क्योंकि प्रकाश किरणे अपवर्तन के बाद आधार की ओर मुड़ती हैं और अपसरित होती दिखाई देती हैं। यह व्यवस्था प्रकाश को अपसरित करने की क्षमता रखता है। इस लेंस को अपसारी लेंस कहा जाता है।
PSEB 10th Class Science Important Questions Chapter 10 प्रकाश-परावर्तन तथा अपवर्तन 49

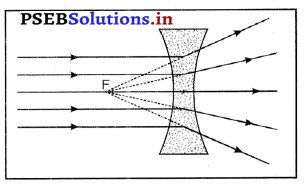
प्रश्न 47.
अवतल लेंस के लिए, यदि वस्तु अनंत पर हो तो प्रतिबिंब कहाँ बनेगा और इसकी प्रकृति क्या होगी ? चित्र बनाकर दर्शाओ।
उत्तर-
यदि वस्तु अनंत पर होगी तो उससे आने वाली सभी आपतित किरणें एक-दूसरे के समानांतर होंगी और अवतल लेंस में से गुज़रने (अपवर्तन) के पश्चात् अपसरित हो जायेंगी (अथवा फैल जाएगी) ये सभी अपवर्तित किरणें पीछे की ओर बढ़ाने पर एक बिंदु से आती हुई प्रतीत होंगी जहाँ प्रतिबिंब बनेगा। यह बिंदु फोकस कहलाता है। अतः प्रतिबिंब आभासी, सीधा तथा आकार में छोटा होगा। चित्र में सभी आपतित किरणें अवतल लेंस के मुख्य अक्ष के समांतर दर्शायी गई हैं।
PSEB 10th Class Science Important Questions Chapter 10 प्रकाश-परावर्तन तथा अपवर्तन 50

प्रश्न 48.
उत्तल लेंस के लिए, वस्तु की स्थिति क्या होनी चाहिए, ताकि प्रतिबिंब फोकस पर बने और बहुत छोटा हो ? चित्र बनाकर दर्शाओ।
उत्तर-
उत्तल लेंस में प्रतिबिंब फोकस पर बनने और आकार में छोटा होने के लिए वस्तु को अनंत पर अर्थात् लेंस से बहुत अधिक दूरी पर होना चाहिए।
PSEB 10th Class Science Important Questions Chapter 10 प्रकाश-परावर्तन तथा अपवर्तन 51

प्रश्न 49.
लेंस सूत्र क्या है ? इसकी व्युत्पत्ति के लिए किन चिह्न परिपाटियों का प्रयोग किया जाता है ?
उत्तर-
लेंस सूत्र (Lens Formula)–लेंस सूत्र वस्तु की दूरी (u), प्रतिबिंब की दूरी (v) तथा लेंस की फोकस दूरी (f) के बीच संबंध को प्रकट करता है।
\(\frac{1}{v}-\frac{1}{u}=\frac{1}{f}\)

चिह्न परिपाटी (Sign Conventions)-

सभी दूरियाँ लेंस के प्रकाशिक केंद्र से मापी जाती हैं तथा प्रकाश बाईं ओर से दाईं ओर आपतित होता है।
आपतित किरण की दिशा में मापी जाने वाली सभी दूरियाँ धन (+) मानी जाती हैं। आपतित किरण की विपरीत दिशा में मापी जाने वाली सभी दूरियाँ ऋण (-) मानी जाती हैं।
मुख्य अक्ष पर अभिलंब की दिशा में ऊपर की तरफ मापी जाने वाली दरियाँ धन तथा नीचे की तरफ मापी जाने वाली दूरियाँ ऋण मानी जाती हैं।

PSEB 10th Class Science Important Questions Chapter 10 प्रकाश-परावर्तन तथा अपवर्तन 52

प्रश्न 50.
प्रतिबिंब की किस स्थिति में एक उत्तल लेंस आभासी तथा सीधा प्रतिबिंब बनाता है? एक किरण आरेख की सहायता से अपना उत्तर स्पष्ट कीजिए।
उत्तर-
उत्तल लेंस के प्रकाशिक केंद्र तथा फोकस के बीच स्थित बिंब का प्रतिबिंब आभासी, सीधा तथा बिंब से बड़ा बनता है, जैसा कि चित्र में प्रदर्शित है। प्रतिबिंब की स्थिति लेंस के उसी ओर होती है जिस ओर बिंब है।
PSEB 10th Class Science Important Questions Chapter 10 प्रकाश-परावर्तन तथा अपवर्तन 53

प्रश्न 51.
आवर्धन की परिभाषा दो। आवर्धन का मात्रक क्या है ?
अथवा
रेखीय आवर्धन की परिभाषा दें। आवर्धन का मात्रक क्या है ?
उत्तर-
आवर्धन (Magnification)–गोलीय लेंस का आवर्धन लेंस द्वारा बनाये गये प्रतिबिंब के आकार तथा वस्तु के आकार का अनुपात होता है। इसे m से प्रदर्शित किया जाता है।
PSEB 10th Class Science Important Questions Chapter 10 प्रकाश-परावर्तन तथा अपवर्तन 54
m का कोई मात्रक नहीं होता क्योंकि यह दो समरूप राशियों का अनुपात है।

प्रश्न 52.
उत्तल दर्पण तथा अवतल दर्पण में अंतर लिखिए।
उत्तर-
उत्तल दर्पण तथा अवतल दर्पण में अंतर

उत्तल दर्पण	अवतल दर्पण
(1) इसमें परावर्तन करने वाला चमकीला तल अंदर बाहर को उभरा होता है।	(1) इसमें परावर्तन करने वाला चमकीला तल धंसा होता है।
(2) इसमें आभासी प्रतिबिंब बनता है।	(2) इसमें वास्तविक और आभासी दोनों प्रकार के प्रतिबिंब बनते हैं।
(3) इसमें सीधा प्रतिबिंब बनता है।	(3) इसमें प्रतिबिंब उल्टा और सीधा दोनों बनते हैं।
(4) इसमें प्रतिबिंब छोटा बनता है।	(4) इसमें प्रतिबिंब बड़ा, छोटा तथा वस्तु के आकार का, तीनों प्रकार का बनता है।

प्रश्न 53.
उत्तल तथा अवतल लेंस में अंतर स्पष्ट कीजिए।
उत्तर-
उत्तल तथा अवतल लेंस में अंतर –

उत्तल लेंस	अवतल लेंस
(1) बीच में से मोटा तथा किनारों से पतला होता है।	(1) बीच में से पतला तथा किनारों से मोटा होता है।
(2) अक्षर बड़े आकार के दिखाई देते हैं।	(2) अक्षर छोटे आकार के दिखाई देते हैं।
(3) प्रकाश की किरणों को एक बिंदु पर केंद्रित करता है।	(3) प्रकाश-किरण पुंज को बिखेर देता है।
(4) वस्तु का प्रतिबिंब वास्तविक, आभासी तथा उल्टा बनता है।	(4) वस्तु का प्रतिबिंब आभासी तथा सीधा बनता है।
(5) इसकी फोकस दूरी धनात्मक होती है।	(5) इसकी फोकस दूरी ऋणात्मक होती है।

प्रश्न 54.
परावर्तन और अपवर्तन में क्या अंतर हैं ?
उत्तर-
परावर्तन तथा अपवर्तन के अन्तर –

परावर्तन	अपवर्तन
(1) किसी चमकीली सतह से टकराकर प्रकाश की किरण का वापस लौट जाना प्रकाश का परावर्तन कहलाता है।	(1) पारदर्शक माध्यम से प्रकाश का एक-दूसरे पारदर्शक माध्यम में प्रवेश करने पर अपने पथ से विचलित हो जाना, प्रकाश का अपवर्तन कहलाता है।
(2) इसमें आपतन कोण तथा परावर्तन कोण सदा समान होते हैं।	(2) इसमें आपतन कोण और अपवर्तन कोण छोटे बड़े होते हैं।
(3) परावर्तन के पश्चात् प्रकाश की किरणें पुनः उसी माध्यम में वापस लौट जाती हैं।	(3) अपवर्तन के पश्चात् प्रकाश की किरणें दूसरे माध्यम में चली जाती हैं।

प्रश्न 55.
बिना स्पर्श किए हुए आप उत्तल लेंस, अवतल लेंस तथा काँच की वृत्ताकार पट्टिका को कैसे पहचानोगे ?
उत्तर-
उत्तल लेंस, अवतल लेंस व काँच की पट्टिका को मुद्रित अक्षरों के ऊपर रखकर आँखों की ओर लाने पर यदि अक्षरों का आकार बढ़ता दिखाई दे तो वह उत्तल लेंस होगा और यदि अक्षरों का आकार घटता दिखाई दे तो वह अवतल लेंस होगा, और यदि अक्षरों का आकार समान रहे तो वह काँच की वृत्ताकार पट्टिका होगी।

प्रश्न 56.
एक-दूसरे के संपर्क में रखे दो या अधिक पतले लेंसों की क्षमता के विषय में आप क्या जानते हैं?
उत्तर-
यदि अनेक पलते लेंस लेकर उन्हें एक-दूसरे से जोड़कर रखें तो इस लेंस के संयोजन की कुल क्षमता उन लेंसों की अलग-अलग क्षमताओं के योग के समान होती है। चश्मा बनाने वाले संशोधी लेंसों के अनेक लेंसों की सहायता से ही आवश्यक लेंस की क्षमता की गणना करते हैं।
∴ P = P₁+ P₂ + P₃

प्रश्न 57.
नीचे दिए गए चित्र में कौन-सा दर्पण दर्शाया गया है ? दर्पण की तुलना में वस्तु कहां रखी है ? बनते दिखाई देते प्रतिबिम्ब का एक लक्षण लिखें।
PSEB 10th Class Science Important Questions Chapter 10 प्रकाश-परावर्तन तथा अपवर्तन 55
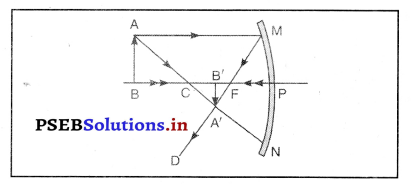
उत्तर-
चित्र में अवतल दर्पण दर्शाया गया है। चित्र में वस्तु AB दर्पण के सामने फोकस (F) तथा ध्रुव के मध्य रखी है। चित्र में बन रहा प्रतिबिंब A’B’ वस्तु की तुलना में बड़ा, सीधा तथा अभासी है।

प्रश्न 58.
गोलाकार दर्पणों के दो उपयोग लिखें।
उत्तर-
गोलाकार दर्पण दो प्रकार के होते हैं-

अवतल दर्पण
उत्तल दर्पण।

गोलाकार दर्पणों का उपयोग

अवतल दर्पण परार्वतक के रूप में परावर्तक दूरदर्शी में प्रयोग किया जाता है।
उत्तल दर्पण ड्राइवरों द्वारा पीछे आ रहे ट्रैफिक को विस्तृत दृष्टि से देखने के लिए प्रयोग किया जाता है क्योंकि इसमें बन रहा प्रतिबिंब छोटा, सीधा तथा आभासी है।

प्रश्न 59.
नीचे दिए गये चित्र में कौन-सा दर्पण दिखाया गया है ? दर्पण की तुलना में वस्तु कहाँ रखी है ? बन रहे प्रतिबिम्ब के लक्षण लिखो।
PSEB 10th Class Science Important Questions Chapter 10 प्रकाश-परावर्तन तथा अपवर्तन 56
उत्तर-
चित्र में अवतल दर्पण दर्शाया गया है। वस्तु की दूरी दर्पण की तुलना में वक्रता केन्द्र (C) से दूर रखा गया है। इसलिए वस्तु AB से बना प्रतिबिंब वास्तविक, उल्टा तथा वस्तु के आकार से छोटा होगा।

संख्यात्मक प्रश्न (Numerical Questions)

प्रश्न 1.
20 cm फोकस दूरी के एक अवतल दर्पण से एक वस्तु कितनी दूरी पर रखी जाये ताकि इसका प्रतिबिंब दर्पण के सामने 40 cm की दूरी पर बने ?
उत्तर-
f = -20 cm (अवतल दर्पण के लिए)
v = -40 cm (आपतित प्रकाश की दिशा के उल्ट दिशा में मापी गई प्रतिबिंब की दूरी)
u = ? (अवतल दर्पण से वस्तु की दूरी)
दर्पण फार्मूले से \(\frac{1}{v}+\frac{1}{u}=\frac{1}{f}\)
\(-\frac{1}{40}+\frac{1}{u}=\frac{1}{-20}\)
या
\(\frac{1}{u}=\frac{-1}{20}+\frac{1}{40}\)
= \(\frac{-2+1}{40}\)
= \(\frac{-1}{40}\)
\(\frac{1}{u}=\frac{1}{-40}\)
या u = -40 cm.
अर्थात् वस्तु अवतल दर्पण के सामने 40 cm की दूरी पर रखी जाए। उत्तर

प्रश्न 2.
एक अवतल दर्पण का वक्रता अर्ध-व्यास 15 cm है और एक वस्तु को इसके शीर्ष से 20cm पर रखा जाता है। प्रतिबिंब की प्रकृति और स्थिति मालूम करो।
हल- वक्रता अर्धव्यास (R) = -15cm (अवतल दर्पण के लिए)
फोकस दूरी (f) = \(\frac{-15}{2}\) cm
वस्तु की दर्पण के शीर्ष से दूरी (u) = -20 cm (आपतित किरण की दिशा के विपरीत दिशा में मापा गया)
प्रतिबिंब की शीर्ष से दूरी (v) = ?
आवर्धन (m) = ?
दर्पण फार्मूला से \(\frac{1}{v}+\frac{1}{u}=\frac{1}{f}\)
\(\frac{1}{v}+\frac{1}{-20}=\frac{1}{\frac{-15}{2}}\)
या \(\frac{1}{v}-\frac{1}{20}=\frac{-2}{15}\)
PSEB 10th Class Science Important Questions Chapter 10 प्रकाश-परावर्तन तथा अपवर्तन 57
∴ v = -12
अर्थात् प्रतिबिंब दर्पण के सामने 12 cm की दूरी पर बनता है।
अब आवर्धन (m) = \(\frac{-v}{u}\)
= \(\frac{-(-12)}{-20}\)
= \(\frac{-12}{20}\)
= \(\frac{-3}{5}\) = -0.6
m < 1 क्योंकि आवर्धन का मान 1 से कम और ऋणात्मक है, इसलिए प्रतिबिंब वस्तु से आकार में छोटा, उल्टा और वास्तविक है।

प्रश्न 3.
एक 6 cm ऊँचाई वाली वस्तु को 18cm फोकस दूरी वाले एक दर्पण से 10 cm की दूरी पर रखा गया है। प्रतिबिंब की स्थिति और आवर्धन ज्ञात करो।
हल –
u = -10 cm आपतित किरण की दिशा के विपरीत दिशा में मापी गई दूरी)
f = + 18 cm (उत्तल दर्पण के लिए)
h₁ = + 6 cm (मुख्य अक्ष के ऊपर की ओर मापने पर)
दर्पण फार्मूले से, \(\frac{1}{v}+\frac{1}{u}=\frac{1}{f}\)
\(\frac{1}{v}+\frac{1}{-10}=\frac{1}{18}\)
∴ \(\frac{1}{v}=\frac{1}{10}+\frac{1}{18}\)
⇒ \(\frac{1}{v}=\frac{18+10}{180}\)
= \(\frac{28}{180}\)
∴ v = + 6.4 cm
क्योंकि v धनात्मक है इसलिए प्रतिबिंब दर्पण के पीछे 6.4 cm की दूरी पर बनता है और आभासी है ।
अब आवर्धन m = \(\frac{-v}{u}\)
= \(\frac{-6.4}{-10}\)
= 0.64 <1
m <1
क्योंकि m का मान एक से कम है, इसका अर्थ है कि प्रतिबिंब का आकार छोटा है।

प्रश्न 4.
एक अवतल दर्पण का वक्रता अर्धव्यास 8 cm है और एक वस्तु इसके शीर्ष से 20 cm पर रखी जाती है। प्रतिबिंब का स्वरूप और स्थिति पता करो।
हल u = -20 cm (आपतित किरण के विपरीत दिशा में मापी गई दूरी)
R = -8 cm (अवतल दर्पण के लिए फोकस दूरी ऋणात्मक होती है।)
प्रतिबिंब की स्थिति v = ?
क्योंकि R = 2f,
∴ f = \(\frac{\mathrm{R}}{2}\)
= \(\frac{-8}{2}\) = -4 cm
दर्पण फार्मूले (सूत्र) से, \(\frac{1}{u}+\frac{1}{v}=\frac{1}{f}\)
PSEB 10th Class Science Important Questions Chapter 10 प्रकाश-परावर्तन तथा अपवर्तन 58
∴ v = -5 cm
ऋण चिह्न यह दर्शाता है कि प्रतिबिंब दर्पण के सामने 5 cm की दूरी पर बनता है। अतः यह प्रतिबिंब वास्तविक तथा उल्टा है।

प्रश्न 5.
7.5cm ऊँचाई की एक वस्तु 20cm अर्धव्यास वाले उत्तल दर्पण के सामने 40 cm की दूरी पर पड़ी है। प्रतिबिंब की दूरी, स्वभाव तथा आकार ज्ञात करो।
हल-हम जानते हैं,
f = \(\frac{\mathrm{R}}{2}\)
= \(\frac{+20}{2}\) = 10 cm
u = -40 cm
(आपतित किरण की दिशा के विपरीत दिशा में मापी गई दूरी)

दर्पण फार्मूले से, \(\frac{1}{u}+\frac{1}{v}=\frac{1}{f}\)
\(\frac{1}{-40}+\frac{1}{v}=\frac{1}{10}\)
⇒ \(\frac{1}{-40}+\frac{1}{v}=\frac{1}{10}\)
\(\frac{1}{v}=\frac{1}{10}+\frac{1}{40}\)
= \(\frac{4+1}{40}\)
\(\frac{1}{v}=\frac{5}{40}\)
= \(\frac{1}{8} \)
∴ V = + 8 cm

क्योंकि v धनात्मक है इसलिए प्रतिबिंब सीधा तथा आभासी है और दर्पण के पीछे 8 cm की दूरी पर बनता है ।
अब आवर्धन
m = \(\frac{-v}{u}\)
= \(\frac{-8}{-40}\)
= \(\frac{1}{5}\)
∴ m <1
क्योंकि m < 1 है, इसलिए प्रतिबिंब का आकार वस्तु के आकार की अपेक्षा छोटा है।

प्रश्न 6.
एक वस्तु का आकार 6 से०मी० है । इस 15 से० मी० फोकस दूरी वाले एक उत्तल दर्पण से 9 से०मी० दूर रखा गया है। प्रतिबिंब की स्थिति ज्ञात करें।
हल- उत्तल दर्पण की फोकस दूरी (f) = 15 से०मी०
वस्तु की दर्पण के शीर्ष से दूरी (u) = -9 से०मी०
वस्तु का आकार = 6 से०मी०

दर्पण फार्मूला
\(\frac{1}{u}+\frac{1}{v}=\frac{1}{f}\)
PSEB 10th Class Science Important Questions Chapter 10 प्रकाश-परावर्तन तथा अपवर्तन 59
\(\frac{1}{v}=\frac{8}{45}\)
∴ v = \(\frac{45}{8}\)
= 5.62 से०मी०
प्रतिबिंब वस्तु की दूसरी ओर होगा। उत्तर

प्रश्न 7.
उस उत्तल लैंस की फोकस दूरी ज्ञात कीजिए जिसकी वक्रता-त्रिज्या 32 cm है।
हल : उत्तल लैंस की वक्रता त्रिज्या, r = 32 cm
f = \(\frac{r}{2}\)
= \(\frac{32}{2}\)
= 16 cm

प्रश्न 8.
हम 20 cm फोकस दूरी के किसी पतले उत्तल लेंस द्वारा किसी वस्तु का वास्तविक, उल्टा तथा आकार में उस वस्तु के बराबर प्रतिबिंब प्राप्त करना चाहते हैं। वस्तु को कहां रखना चाहिए ? इस प्रकरण में प्रतिबिंब बनना दर्शाने के लिए प्रकाश किरण-आरेख खींजिए।
उत्तर-
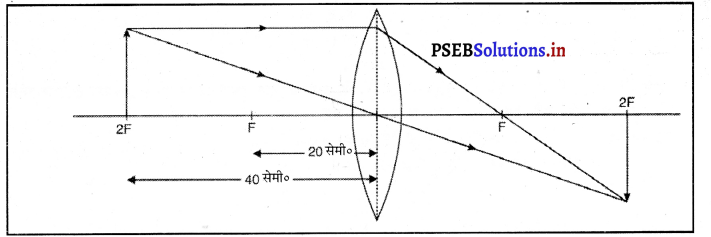
20 सेमी० फोकस दूरी के उत्तल लेंस की सहायता से वास्तविक सीधा और समान आकार का प्रतिबिंब प्राप्त करने के लिए वस्तु को 2F पर रखा जाता है। उसका प्रतिबिंब भी दूसरी 2F पर बनता है। वस्तु को (2×20) = 40 सेमी० दूर रखा जाना चाहिए ताकि समान आकार का प्रतिबिंब लेंस की दूसरी ओर प्राप्त हो सके। वस्तु की लैंस से दूरी = 2f
= 2xf
= 2 x 20 cm
= 40 cm
PSEB 10th Class Science Important Questions Chapter 10 प्रकाश-परावर्तन तथा अपवर्तन 60

प्रश्न 9.
4.0 cm ऊँचाई की एक वस्तु 15.0 cm फोकस दूरी वाले अवतल दर्पण से 30.0 cm की दूरी पर रखी गई है। दर्पण से कितनी दूरी पर एक पर्दे को रखा जाए जिससे कि वस्तु का स्पष्ट प्रतिबिंब पर्दे पर प्राप्त हो सके ? प्रतिबिंब की प्रकृति तथा आकार भी ज्ञात कीजिए।
हल-
दिया है : वस्तु का आकार h = 4.0 cm
वस्तु की अवतल दर्पण से दूरी u = -30.0 cm
अवतल दर्पण की फोकस दूरी f = -15.0 cm
प्रतिबिंब की दर्पण से दूरी v = ?
प्रतिबिंब का आकार h’ = ?

दर्पण के सूत्र \(\frac{1}{v}+\frac{1}{u}=\frac{1}{f}\) से.
\(\frac{1}{v}=\frac{1}{f}-\frac{1}{u}\)
PSEB 10th Class Science Important Questions Chapter 10 प्रकाश-परावर्तन तथा अपवर्तन 61
∴ v = -30.cm
अतः पर्दे को दर्पण के सामने 30.0 cm की दूरी पर रखना चाहिए।
प्रकृति-चूँकि प्रतिबिंब पर्दे पर प्राप्त हो रहा है : अतः यह वास्तविक तथा उल्टा होगा।
आकार-दर्पण के आवर्धन सूत्र
m = \(\frac{h^{\prime}}{h}=-\frac{v}{u}\) से,
प्रतिबिंब का आकार h’ = \(-\frac{v}{u} \times h \)
= – \( \left(\frac{-30.0 \mathrm{~cm}}{-25.0 \mathrm{~cm}}\right) \times 4.0\) cm
= -4.0 cm

प्रश्न 10.
3 cm ऊँचे बिंब को 18 cm फोकस दूरी के एक अवतल दर्पण के सामने 9 cm की दूरी पर रखा गया है। बने प्रतिबिंब की स्थिति तथा आकार ज्ञात कीजिए।
हल- दिया है : बिंब की अवतल दर्पण से दूरी, u = -9 cm
अवतल दर्पण की फोकस दूरी f = -18 cm
वस्तु की ऊँचाई, h = 3 cm

दर्पण सत्र \(\frac{1}{v}+\frac{1}{u}=\frac{1}{f}\) से,
\(\frac{1}{v}=\frac{1}{f}-\frac{1}{u}\)
= \(-\frac{1}{18}+\frac{1}{9}\)
= \(\frac{-1+2}{18}\)
= \(\frac{1}{18}\)
⇒ v = + 18 cm

स्थिति-प्रतिबिंब दर्पण के पीछे 18cm की दूरी पर बनेगा।
प्रकृति-प्रतिबिंब सीधा तथा आभासी होगा।
आकार-दर्पण के लिए आवर्धन सूत्र m = \(\frac{h^{\prime}}{h}=\frac{v}{u}\) से,
प्रतिबिंब का आकार h = \(\frac{-v}{u} \times h\)
= – \(\left(\frac{18}{-9}\right) \times 3\) = 6 cm
∴ प्रतिबिंब की ऊँचाई 6 cm होगी।

प्रश्न 11.
18 cm फोकस दूरी के उत्तल लेंस से किसी बिंब को कितनी दूरी पर रखा जाना चाहिए कि उसका प्रतिबिंब लेंस से 24 cm की दूरी पर बने ? इस स्थिति में आवर्धन कितना होगा ?
हल- दिया है, लेंस की फोकस दूरी (f) = + 18 cm
प्रतिबिंब की लैंस से दूरी (v) = + 24 cm
बिंब की लैंस से दूरी (u) = ?

लेंस सूत्र \(\frac{1}{v}-\frac{1}{u}=\frac{1}{f}\) से
या \(\frac{1}{u}=\frac{1}{v}-\frac{1}{f}\)
= \(\frac{1}{24}-\frac{1}{18}\)
= \(\frac{3-4}{72}\)
= \(-\frac{1}{72}\)
u = -72 cm

ऋणात्मक चिह्न यह दर्शाता है कि वस्तु को लेंस के सामने 72 cm की दूरी पर रखना चाहिए।
आवर्धन = \(\frac{-v}{u}\)
= \(\frac{-24}{-72} \)
= \(-\frac{1}{3}\)
प्रतिबिंब वास्तविक, उल्टा तथा आकार में वस्तु के आकार का \(-\frac{1}{3}\) होगा।
अतः प्रतिबिंब वास्तविक, उल्टा तथा आकार में बिंब का एक-तिहाई है।

प्रश्न 12.
एक उत्तल लेंस की फोकस दूरी 25cm है। बिंब की लेंस से दूरी का परिकलन कीजिए जबकि उसका प्रतिबिंब लेंस के दूसरी ओर लेंस से 75 cm की दूरी पर बनता है। इस प्रतिबिंब की प्रकृति क्या होगी?
हल- दिया है : f = +25 cm, v = + 75 cm, u = ?

लेंस के सूत्र \(\frac{1}{v}-\frac{1}{u}=\frac{1}{f}\) से
\(\frac{1}{u}=\frac{1}{v}-\frac{1}{f}\)
= \(\frac{1}{75}-\frac{1}{25}\)
= \(\frac{1-3}{75}\)
= \(\frac{-2}{75}\)
⇒ u = \(-\frac{75}{2}\) = -37.5cm
बिंब लेंस के बाईं ओर लेंस से 37.5 cm की दूरी पर स्थित है।
∵ प्रतिबिंब लेंस के दूसरी ओर है इसलिए यह वास्तविक तथा उल्टा होगा।

प्रश्न 13.
वायु के सापेक्ष सघन फ्लिंट कांच का अपवर्तनांक 1.65 तथा एल्कोहल के लिए यह 1.36 है। एल्कोहल के सापेक्ष सघन फ्लिंट कांच का अपवर्तनांक क्या है ?
हल-
एल्कोहल के w.r.t. फ्लिंट काँच का अपवर्तनांक = img
= \(\frac{1.65}{1.36}\)
= \(\frac{165}{136}\)
= 1.21

प्रश्न 14.
एक वस्तु 20 सेमी० फोकस दूरी वाले एक अवतल लेंस के सामने 40 मी० की दूरी पर रखी गई है। प्रतिबिंब की स्थिति तथा लेंस का आवर्धन ज्ञात करो।
हल : अवतल लेंस की फोकस दूरी (f) = -20 सेमी०
वस्तु की लेंस से दूरी (u) = -40 सेमी०
प्रतिबिंब की लेंस से दूरी (स्थिति) (v) = ?

लेंस फार्मूले से, \(\frac{1}{v}-\frac{1}{u}=\frac{1}{f}\)
\(\frac{1}{v}-\frac{1}{-40}=\frac{1}{-20}\)
\(\frac{1}{v}+\frac{1}{40}=-\frac{1}{20}\)
\(\frac{1}{v}=-\frac{1}{20}-\frac{1}{40}\)
\(\frac{1}{v}=\frac{-2-1}{40}\)
\(\frac{1}{v}=\frac{-3}{40}\)

∴ v = \(\frac{-40}{3}\) = -13.3 सेमी० प्रतिबिंब आभासी सीधा तथा लेंस के उसी तरफ बनता है।
आवर्धन (m) = \(\frac{-v}{u}\)
= \(\frac{-\left(\frac{-40}{3}\right)}{-40}\)
= \(\frac{40}{3 \times(-40)}\)
= \(\frac{-1}{3}\)
प्रतिबिंब आकार में छोटा होगा।

प्रश्न 15.
किसी माध्यम में प्रकाश का वेग 2 x 10⁸ ms^-1 है। एक आपतित किरण इसके सघन पक्ष के साथ 0° का कोण बनाती है। अपवर्तन कोण ज्ञात करो। निर्वात में प्रकाश का वेग 3 x 10⁸ ms^-1 है।
हल:
PSEB 10th Class Science Important Questions Chapter 10 प्रकाश-परावर्तन तथा अपवर्तन 62
a_μ_m = \(\frac{3 \times 10^{8}}{2 \times 10^{8}}\)
= \(\frac{3}{2}\)
a_μ_m = \(\frac{1}{m_{\mu_{a}}}\)
\(\frac{3}{2}=\frac{1}{m_{u_{a}}}\)
m_μ_a = \(\frac{\sin i}{\sin r}\)
\(\frac{2}{3}=\frac{\sin 30^{\circ}}{\sin r}\)
\(\frac{2}{3}=\frac{0.5}{\sin r} \)
sin r = \(\frac{0.5}{2 / 3}\)
= \(\frac{0.5 \times 3}{2}\)
sin r = 0.7500
∴ अपवर्तन कोण, r = 48° 36′ उत्तर

प्रश्न 16.
5 cm ऊंची कोई वस्तु 10 cm फोकस दूरी के किसी अभिसारी लेंस से 25 cm दूरी पर रखी जाती है। प्रकाश-किरण आरेख खींचकर बनने वाले प्रतिबिंब की स्थिति, आकार तथा प्रकृति ज्ञात कीजिए।
हल:
वस्तु की ऊँचाई, h₁ = 5 cm
वस्तु की अभिसारी लेंस से दूरी u = -25 cm
ऋणात्मक होगा। अभिसारी लेंस की फोकस दूरी, f = + 10 cm (उत्तल लेंस)
v = ?
लेंस सूत्र से, \(\frac{1}{v}-\frac{1}{u}=\frac{1}{f}\)
\(\frac{1}{v}=\frac{1}{f}+\frac{1}{u}\)
\(\frac{1}{v}=\frac{1}{10}+\frac{1}{(-25)}\)
= \(\frac{1}{10}-\frac{1}{25}\)
\(\frac{1}{v}=\frac{5-2}{50}\)
= \(\frac{3}{50}\)
∴ v = \(\frac{50}{3}\) = 6.67 cm

अब लेंस का आवर्धन m = \(\frac{v}{u}\)
= \(\frac{50 / 3}{(-25)} \)
= \(\frac{-50}{3 \times 25}\)
m = \(\frac{-2}{3}\)

प्रतिबिंब वास्तविक, उल्टा और 16.67 cm दूर लेंस की दूसरी तरफ होगा।
m = \(\frac{h_{2}}{h_{1}}=\frac{-2}{3}\)
\(\frac{h_{2}}{5}=\frac{-2}{3}\)
h₂ = \(\frac{-10}{3}\)
h₂ = -3.33 cm
PSEB 10th Class Science Important Questions Chapter 10 प्रकाश-परावर्तन तथा अपवर्तन 63

प्रश्न 17.
15 cm फोकस दूरी का कोई अवतल लेंस किसी वस्तु का लेंस से 10 cm दूरी पर प्रतिबिंब बनाता है। वस्तु लेंस से कितनी दूरी पर स्थित है ? प्रकाश किरण-आरेख खींचिए।
हल :
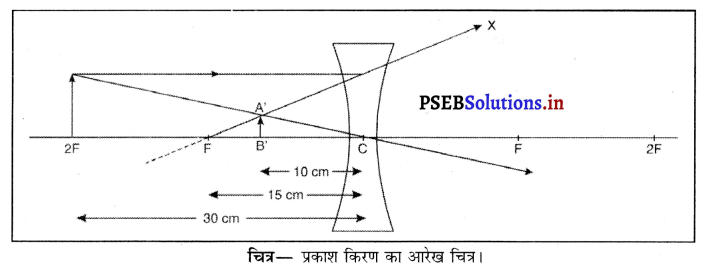
PSEB 10th Class Science Important Questions Chapter 10 प्रकाश-परावर्तन तथा अपवर्तन 64
यहाँ f = -15 cm, v = –10 cm, u = ?
लेंस सूत्र से, \(\frac{1}{f}=\frac{1}{v}-\frac{1}{u}\)
\(\frac{1}{u}=\frac{1}{v}-\frac{1}{f}\)
\(\frac{1}{u}=\frac{1}{(-10)}-\frac{1}{(-15)}\)
= \(\frac{-1}{10}+\frac{1}{15}\)
\(\frac{1}{u}=\frac{-3+2}{30}\)
= \(\frac{-1}{30}\)
u = -30 cm
अतः वस्तु को अवतल लेंस से 30 cm दूर रखना चाहिए।

प्रश्न 18.
एक वस्तु को 15 cm फोकस दूरी के एक अवतल लेंस से 30 cm पर रखा जाता है। प्रतिबिंब की प्रकृति, स्थिति और आवर्धन क्या होगा ?
हल : यहां अवतल लेंस की फोकस दूरी (f) = -15 cm (अवतल लेंस की फोकस दूरी ऋणात्मक मानी जाती है)
वस्तु की अवतल लेंस से दूरी (u) = -30 cm (आपतित किरण की दिशा से विपरीत दिशा में मापी गई दूरी ऋणात्मक मानी जाती है)
प्रतिबंब की अवतल लेंस से दूरी (v) = ?
लेंस फार्मूले से \(\frac{1}{v}-\frac{1}{u}=\frac{1}{f}\)
\(\frac{1}{v}-\frac{1}{-30}=\frac{1}{-15}\)
या \(\frac{1}{v}+\frac{1}{30}=\frac{1}{-15}\)
या \(\frac{1}{v}=-\frac{1}{15}-\frac{1}{30}\)
या \(\frac{1}{v}=\frac{-2-1}{30}\)
या \(\frac{1}{v}=\frac{-3}{30}\)
या \(\frac{1}{v}=\frac{-1}{10}\)
या v = -10 cm

v के ऋण चिह्न से पता चलता है कि प्रतिबिंब लेंस के उसी तरफ 10 cm की दूरी पर बनेगा जिस तरफ वस्तु पड़ी है। इसलिए प्रतिबिंब आभासी तथा सीधा होगा।
अब आवर्धन (m) = \(\frac{-v}{-u}\)
= \(\frac{-(-10)}{-(-30)}\)
= \(\frac{10}{30}\)
= \(\frac{1}{3}\) = 0.33
क्योंकि m का मान धनात्मक है, इसलिए प्रतिबिंब सीधा है।
∵ | m | = \(\frac{1}{3}\) जोकि <1 है, इसलिए प्रतिबिंब आकार में वस्तु से छोटा है।

प्रश्न 19.
7 cm ऊँचाई की एक वस्तु को 20 cm फोकस-दूरी के एक उत्तल लेंस से 40 cm की दूरी पर रखा जाता है। प्रतिबिंब की स्थिति, प्रकृति और ऊँचाई ज्ञात करो।
हल : यहाँ पर वस्तु की ऊँचाई (h) = + 7 cm
उत्तल लेंस की फोकस दूरी (f) = + 20 cm (उत्तल लेंस की फोकस दूरी धनात्मक मानी जाती है)
वस्तु की उत्तल लेंस से दूरी (u) = – 40 cm
(आपतित किरण की विपरीत दिशा में मापी गई दूरी ऋणात्मक मानी जाती है)
प्रतिबिंब की लेंस से दूरी (v) = ?

लेंस सूत्र से \(\frac{1}{v}-\frac{1}{u}=\frac{1}{f}\)
\(\frac{1}{v}-\frac{1}{-40}=\frac{1}{+20}\)
या \(\frac{1}{v}+\frac{1}{40}=\frac{1}{20}\)
या \(\frac{1}{v}=\frac{1}{20}-\frac{1}{40}\)
या \(\frac{1}{v}=\frac{2-1}{40}\)
या \(\frac{1}{v}=\frac{1}{40}\)
∴ v = + 40 cm 1

v के धन चिह्न से पता चलता है कि प्रतिबिंब वास्तविक तथा उल्टा है और लेंस की दूसरी तरफ 40 cm की दूरी पर बनता है।

अब m = \(\frac{v}{u}\)
= \(\frac{40}{-40}\)
∴ m = -1
|m| = |-1| = 1
परंतु m = \(\frac{h_{2}}{h_{1}}\)
∴ h₂ = h₁
अर्थात् प्रतिबिंब का आकार वस्तु के आकार के समान है।

प्रश्न 20.
4 cm ऊँचाई की एक वस्तु को -10 डाइऑप्टर क्षमता वाले एक अवतल लेंस के सामने 15 cm की दूरी पर रखा जाता है। प्रतिबिंब का आकार और प्रकृति पता करो। हल : वहाँ वस्तु की ऊंचाई (h₁) = + 4 cm
अवतल लेंस की क्षमता (P) = -10 डाइऑप्टर
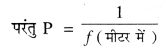
PSEB 10th Class Science Important Questions Chapter 10 प्रकाश-परावर्तन तथा अपवर्तन 65
f = \( \frac{1}{-10} \times 100\)
= -10 cm
∴ अवतल लेंस की फोकस दूरी (f) = -10 cm

वस्तु की लेंस से दूरी (u) = -15 cm
प्रतिबिंब की लेंस से दूरी (v) = ?
लेंस सूत्र से, \(\frac{1}{v}-\frac{1}{u}=\frac{1}{f}\)
\(\frac{1}{v}-\frac{1}{-15}=\frac{1}{-10}\)
\(\frac{1}{v}+\frac{1}{15}=\frac{-1}{10}\)
PSEB 10th Class Science Important Questions Chapter 10 प्रकाश-परावर्तन तथा अपवर्तन 66
∴ v = -6 cm

v के ऋण चिहन से पता चलता है कि प्रतिबिंब आभासी तथा सीधा है और लेंस की तरफ 6 cm की दूरी पर बनता है।

अब m = \(\frac{v}{u}\)
= \(\frac{-6}{-15}\)
= \(\frac{2}{5}\)
∴ m = \(\frac{2}{5}\)

m = \(\frac{h_{2}}{h_{1}}\)
m = \(\frac{2}{5}\)
h₂ = \(\frac{2 h_{1}}{5}\)
∴ = \(\frac{2}{5}\) × 4 cm
∴ h₂ = \(\frac{8}{5}\) cm = 1.6 cm
अत: प्रतिबिंब का आकार 1.6 cm है।

प्रश्न 21.
5 मीटर फोकस दूरी वाले अवतल लेंस की शक्ति ज्ञात करो।
हल :
अवतल लेंस की फोकस दूरी (f) = -5 m
अवतल लेंस की शक्ति (P) =?
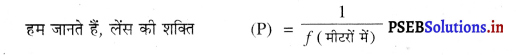
PSEB 10th Class Science Important Questions Chapter 10 प्रकाश-परावर्तन तथा अपवर्तन 67
= \(\frac{1}{-5}\)
= -0.2 D उत्तर

प्रश्न 22.
4 मीटर फोकस दूरी के एक उत्तल लेंस की क्षमता कितनी होगी?
हल :
उत्तर लेंस की फोकस दूरी (f) = 4
मीटर उत्तल लेंस की क्षमता (P) = ?
हम जानते हैं कि लेंस की क्षमता
(P) = \(\frac{1}{f}\)
= \(\frac{1}{4}\)
= 0.25 D उत्तर

प्रश्न 23.
2m फोकस दूरी वाले किसी उत्तल लेंस की शक्ति ज्ञात करो। लेंस की शक्ति की इकाई लिखो।
हल : उत्तल लेंस की फोकस दूरी (f) = 2m
उत्तल लेंस की क्षमता (P) = ?
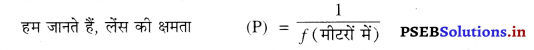
PSEB 10th Class Science Important Questions Chapter 10 प्रकाश-परावर्तन तथा अपवर्तन 68
= \(\frac{1}{2}\)
= 0.5 D (डाइऑप्टर) उत्तर

अति लघु उत्तरात्मक प्रश्न (Very Short Answer Type Questions)

प्रश्न 1.
दर्पण की फोकस दूरी की परिभाषा लिखिए।
उत्तर-
फोकस दूरी (Focal Length)-गोलीय दर्पण के ध्रुव (शीर्ष) तथा मुख्य फोकस के मध्य की दूरी को फोकस दूरी कहते हैं। इसे द्विारा प्रदर्शित किया जाता है। S.I. पद्धति में फोकस दूरी का मात्रक मीटर है।

प्रश्न 2.
दर्पण के ध्रुव ( या शीर्ष) को परिभाषित कीजिए।
उत्तर-
ध्रुव या शीर्ष (Pole)-गोलीय दर्पण के मध्य बिंदु या केंद्र को इसका ध्रुव या शीर्ष कहते हैं।

प्रश्न 3.
यदि कोई वस्तु समतल दर्पण से 10 मीटर की दूरी पर है तो वस्तु तथा उसके प्रतिबिंब के मध्य कितनी दूरी होगी ?
उत्तर-
वस्तु और प्रतिबिंब के मध्य दूरी = (10 + 10) मीटर = 20 मीटर।

प्रश्न 4.
जब प्रकाश की किरण समतल दर्पण पर अभिलंब रूप में पड़ती है तो उसका आपतित कोण तथा परावर्तन कोण कितने-कितने अंश होता है?
उत्तर-
आपतन कोण (∠i) = (0°)
परावर्तन कोण (∠r) = 0°

प्रश्न 5.
ऊर्जा के किन्हीं तीन रूपों के नाम बताओ।
उत्तर-

प्रकाश ऊर्जा
ताप ऊर्जा
ध्वनि ऊर्जा।

प्रश्न 6.
प्रकाशीय ऊर्जा की प्रकृति क्या है ?
उत्तर-
विद्युत्-चुंबकीय तरंगें (Electro-Magnetic Waves)

प्रश्न 7.
वायु में प्रकाश की चाल कितनी है ?
उत्तर-
3 x 10⁸ मीटर प्रति सैकिंड।

प्रश्न 8.
प्रकाश के एक प्रमुख प्राकृतिक स्रोत का नाम बताओ।
उत्तर-
सूर्य।

प्रश्न 9.
दो मानव निर्मित प्रकाश स्रोतों के नाम बताओ।
उत्तर-

मोमबत्ती,
विद्युत् लैंप।

प्रश्न 10.
गोलीय दर्पण की दो किस्मों के नाम बताओ।
उत्तर-

अवतल दर्पण
उत्तल दर्पण।

प्रश्न 11.
आपतन कोण क्या होता है?
उत्तर-
आपतन कोण- आपतित किरण तथा अभिलंब के बीच बने कोण को आपतन कोण ( ∠i) कहते हैं।

प्रश्न 12.
परावर्तन कोण क्या होता है ?
उत्तर-
परावर्तन कोण- परावर्तित किरण तथा आपतन बिंदु पर बने अभिलंब के मध्यवर्ती कोण को परावर्तन कोण ( ∠r) कहते हैं।

प्रश्न 13.
गोलीय दर्पण की परिभाषा दो।
उत्तर-
गोलीय दर्पण (Spherical Mirror)- यदि दर्पण किसी खोखले गोले का भाग हो जिसकी एक सतह पालिश की गई हो और दूसरी सतह परावर्तक हो तो ऐसा दर्पण गोलीय दर्पण कहलाता है।

प्रश्न 14.
समतल दर्पण में किस प्रकृति का प्रतिबिंब बनता है?
उत्तर-
आभासी, सीधा तथा समान आकार का।

प्रश्न 15.
किस गोलीय दर्पण की फोकस दूरी धनात्मक मानी जाती है?
उत्तर-
उत्तल दर्पण की।

प्रश्न 16.
दर्पण फार्मला लिखो।
अथवा
किसी गोलीय दर्पण से परावर्तन के लिए सूत्र लिखो।
उत्तर-
\(\frac{1}{u}+\frac{1}{v}=\frac{1}{f}\)
.
प्रश्न 17.
अवतल दर्पण की किस सतह से परावर्तन होता है?
उत्तर-
वह भीतरी सतह जो दर्पण के वक्रता केंद्र की ओर होती है।

प्रश्न 18.
किस गोलीय दर्पण में सदैव प्रतिबिंब आभासी, सीधा तथा छोटा बनता है ?
उत्तर-
उत्तल दर्पण में।

प्रश्न 19.
गोलीय दर्पण के वक्रता अर्धव्यास तथा फोकस दूरी में क्या संबंध है ?
उत्तर-
f= \(\frac{\mathrm{R}}{2}\)

प्रश्न 20.
जिस दर्पण की फोकस दूरी -15 cm हो, उसकी प्रकृति कैसी होगी ?
उत्तर-
यह दर्पण अवतल होगा।

प्रश्न 21.
एक दर्पण का आवर्धन 0.4 है। यह दर्पण किस प्रकार का है ? इसका प्रतिबिंब कैसा होगा?
उत्तर-
यह दर्पण उत्तल होगा क्योंकि इसका आवर्धन धनात्मक है और यह 1 से कम है। प्रतिबिंब छोटा, सीधा तथा आभासी होगा।

प्रश्न 22.
आवर्धन की परिभाषा लिखो। इसकी इकाई क्या है?
उत्तर-
आवर्धन(Magnifications)-प्रतिबिंब के आकार तथा वस्तु के आकार के अनुपात को आवर्धन कहते हैं।
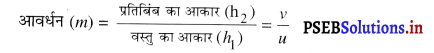
PSEB 10th Class Science Important Questions Chapter 10 प्रकाश-परावर्तन तथा अपवर्तन 69
आवर्धन (m) की कोई इकाई नहीं होती क्योंकि यह एक समान दो राशियों का अनुपात है।

प्रश्न 23.
किसी दर्पण को अभिसारी तथा किस दर्पण को अपसारी कहा जाता है ?
उत्तर-
अभिसारी दर्पण-अवतल दर्पण अपसारी दर्पण-उत्तल दर्पण।।

प्रश्न 24.
सर्चलाइट में किस दर्पण का प्रयोग किया जाता है ?
उत्तर-
अवतल दर्पण का।

प्रश्न 25.
किस दर्पण को अपने से दूर ले जाने पर दर्पण का दृष्टि क्षेत्र बढ़ जाता है ?
उत्तर-
उत्तल दर्पण।

प्रश्न 26.
समतल दर्पण की कितनी फोकस दूरी होती है?
उत्तर-
अनंत।

प्रश्न 27.
किसी दर्पण की आवर्धन क्षमता 1 होती है ?
उत्तर-
समतल दर्पण की।

प्रश्न 28.
समतल दर्पण में बन रहे प्रतिबिंब के लिए वस्तु दूरी तथा प्रतिबिंब दूरी के मध्य संबंध लिखो।
उत्तर-
u= -v,

प्रश्न 29.
वास्तविक प्रतिबिंब से क्या अभिप्राय है?
उत्तर-
वास्तविक प्रतिबिंब- परावर्तन या अपवर्तन के पश्चात् यदि प्रकाश की किरणें परस्पर एक बिंदु पर मिलें तो उस बिंदु पर वास्तविक प्रतिबिंब बनता है।

प्रश्न 30.
अवतल दर्पण के लिए जब वस्तु अनंत और वक्रता केंद्र (C) के बीच हो तो प्रतिबिंब की स्थिति बताओ।
उत्तर-
जब वस्तु अनंत और वक्रता केंद्र के C बीच हो तो अवतल दर्पण में प्रतिबिंब अवतल दर्पण के फोकस व वक्रता केंद्र के मध्य बनता है।

प्रश्न 31.
एक गोलीय दर्पण की वक्रता त्रिज्या 24 cm है। इसकी फोकस दूरी क्या होगी?
उत्तर-
दिया है, वक्रता त्रिज्या R = 24 cm
∴ फोकस दूरी f = \(\frac{\mathrm{R}}{2}\) = \(\frac{24}{2}\) = 12.0 cm

प्रश्न 32.
जब प्रकाश की किरण सघन माध्यम से विरल माध्यम में प्रवेश करती है, तो अभिलंब के किस ओर झुकती है?
उत्तर-
ऐसी प्रकाश की किरण अभिलंब से दूर झुक जाती है।

प्रश्न 33.
जब प्रकाश की किरण विरल माध्यम से सघन माध्यम में जाती है, तो अभिलंब के किस ओर झुकती है?
उत्तर-
प्रकाश की किरण अभिलंब की ओर झुक जाती है।

प्रश्न 34.
जब प्रकाश विरल से सघन माध्यम में जाता है, तो अपवर्तन कोण तथा आपतन कोण में से कौन-सा बड़ा होता है?
उत्तर-
आपतन कोण।

प्रश्न 35.
उत्तल लेंस द्वारा दूर स्थित वस्तु का प्रतिबिंब कैसा बनता है ?
उत्तर-
वास्तविक, उल्टा तथा छोटा।

प्रश्न 36.
किस छपे हुए कागज़ पर अभिसारी लेंस रखने पर अक्षर कैसे दिखाई देते हैं ?
उत्तर-
सीधे तथा बड़े।

प्रश्न 37.
पानी में रखा सिक्का उठा हुआ क्यों दिखाई देता है?
उत्तर-
प्रकाश अपवर्तन के कारण।

प्रश्न 38.
मुख्य फोकस और प्रकाशिक केंद्र के बीच की दूरी को क्या कहते हैं ?
उत्तर-
फोकस दूरी (1)।

प्रश्न 39.
किसी स्थिति में प्रतिबिंब, वस्तु के आकार के समान होता है?
उत्तर-
जब वस्तु 2f पर हो।

प्रश्न 40.
उत्तल लेंस से आभासी तथा बड़ा प्रतिबिंब कब बनता है? उत्तर-जब वस्तु मुख्य फोकस तथा प्रकाशिक केंद्र के बीच हो। प्रश्न 41. लेंस किसे कहते हैं ? ये कितने प्रकार के होते हैं?
उत्तर-
लेंस- एक ऐसा पारदर्शक माध्यम जो दो वक्र तलों अथवा एक वक्र तल तथा दूसरा समतल सतह से घिरा हुआ हो तथा प्रकाश का अपवर्तन करता हो, लेंस कहलाता है। ये दो प्रकार के होते हैं-

उत्तल लेंस
अवतल लेंस।

प्रश्न 42.
लेंस के लिए दूरियाँ किस बिंदु से मापी जाती हैं ?
उत्तर-
प्रकाशिक केंद्र से।

प्रश्न 43.
किस लेंस को आवर्धन लेंस कहते हैं ?
उत्तर-
उत्तल लेंस को।

प्रश्न 44.
लेंस सूत्र लिखिए।
उत्तर-
\(\frac{1}{f}=\frac{1}{v}-\frac{1}{u}\)

प्रश्न 45.
लेंस की क्षमता की परिभाषा लिखो।
उत्तर-
लेंस की क्षमता-किसी लेंस की क्षमता (शक्ति) इसकी मीटरों में फोकस दूरी का व्युत्क्रम होती है।
P = \(\frac{1}{f}\)

प्रश्न 46.
बिना शक्ति के चश्मे (Plane Glasses) की फोकस दूरी कितनी होती है?
उत्तर-
P= \(\frac{1}{f}\)
= \(\frac{1}{0}\) = ∞
∴ अनंत फोकस दूरी।

प्रश्न 47.
किस लेंस को अपसारी लेंस कहते हैं ?
उत्तर-
अवतल लेंस को।

प्रश्न 48.
लेंस की शक्ति तथा फोकस दूरी में संबंध लिखो।
उत्तर-
PSEB 10th Class Science Important Questions Chapter 10 प्रकाश-परावर्तन तथा अपवर्तन 70

प्रश्न 49.
किस लेंस की शक्ति धन तथा किस लेंस की शक्ति ऋण होती है ?
उत्तर-
उत्तल लेंस की शक्ति धन तथा अवतल लेंस की शक्ति ऋण होती है।

प्रश्न 50.
लेंस की फोकस दूरी की परिभाषा लिखो।
उत्तर-
लेंस की फोकस दूरी (Focal Length of Lens)- किसी लेंस की फोकस दूरी उस लेंस के प्रकाशिक केंद्र तथा मुख्य फोकस के बीच की दूरी है।

प्रश्न 51.
अपवर्तनांक की परिभाषा दो।
उत्तर-
अपवर्तनांक (Refractive Index)-निर्वात में प्रकाश के वेग और किसी अन्य माध्यम में प्रकाश के अनुपात को उस माध्यम का निरपेक्ष अपवर्तनांक कहते हैं।

प्रश्न 52.
दो विलयनों के अपवर्तनांक 1.36 तथा 1.54 हैं, कौन अधिक सघन है ?
उत्तर-
अधिक अपवर्तनांक 1.54 वाला विलयन सघन होगा।

प्रश्न 53.
लेंस की क्षमता का मात्रक लिखिए।
उत्तर-
डाऑप्टर।

प्रश्न 54.
एक लेंस की क्षमता -2.5 D है। यह लेंस कैसा होगा ?
उत्तर-
अवतल।

प्रश्न 55.
संपर्क में रखे दो लेंसों की क्षमताएँ क्रमशः P₁ तथा P₂ हैं। संयुक्त लेंस की क्षमता क्या होगी ?
उत्तर-
क्षमता P = P₁ + P₂

प्रश्न 56.
घड़ीसाज, घड़ी के सूक्ष्म पुों को देखने के लिए कौन-सा लेंस प्रयोग करता है ?
उत्तर-
उत्तल लेंस।

प्रश्न 57. हीरे का अपवर्तनांक 2.42 है जबकि काँच का अपवर्तनांक 1.5 है। दोनों में कौन अधिक प्रकाशीय सघन है ? किसमें प्रकाश की चाल अधिक होगी ?
उत्तर-
हीरे का अपवर्तनांक, काँच से अधिक है, इसलिए काँच की तुलना में हीरा प्रकाशीय सघन है।
∴ विरल माध्यम में प्रकाश की चाल सघन माध्यम की तुलना में अधिक होती है। इसलिए काँच में चाल अधिक होगी।

प्रश्न 58.
विचलन कोण (Angle of deviation) क्या है ?
उत्तर-
विचलन कोण-निर्गत किरण (Emergent ray) बनाने में आपतित किरण (Incident ray) जिस कोण पर मुड़ जाती है, उस कोण को विचलन कोण (Angle of deviation) कहा जाता है।

प्रश्न 59.
उत्तल लेंस के मुख्य फोकस की परिभाषा लिखो।
उत्तर-
मुख्य फोकस-उत्तल लेंस का मुख्य फोकस लेंस के मुख्य अक्ष पर वह बिंदु है जिस पर मुख्य अक्ष के समांतर आ रही प्रकाश किरणे अपवर्तन के बाद मिलती हैं।

प्रश्न 60.
गोलीय दर्पण की वक्रता-त्रिज्या की परिभाषा लिखें।
उत्तर-
वक्रता-त्रिज्या-गोलीय दर्पण की वक्रता त्रिज्या उस खोखले गोले का अर्धव्यास है जिस का दर्पण एक भाग है। इसे R द्वारा प्रदर्शित किया जाता है।

प्रश्न 61.
नीचे गोलीय दर्पण के रेखाचित्र
(a) तथा
(b) दिए गए हैं। दर्पण (a) तथा दर्पण (b) की किस्म बताओ।
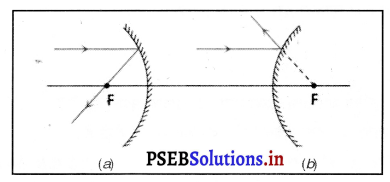
PSEB 10th Class Science Important Questions Chapter 10 प्रकाश-परावर्तन तथा अपवर्तन 72
उत्तर-
(a) अवतल दर्पण
(b) उत्तल दर्पण।

प्रश्न 62.
नीचे दिए गए चित्र किस प्रकाशीय प्रक्रिया को दर्शाते हैं।
img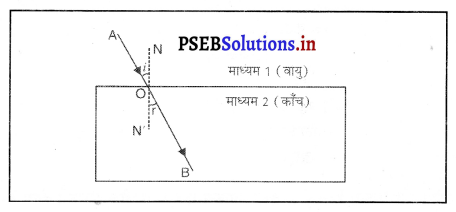 PSEB 10th Class Science Important Questions Chapter 10 प्रकाश-परावर्तन तथा अपवर्तन 73 उत्तर-
प्रकाश अपवर्तन।

वस्तुनिष्ठ प्रश्न (Objective Type Questions)
बहु-विकल्पीय प्रश्न

प्रश्न 1.
एक उत्तल लेंस की क्षमता 2 डाइआप्टर है। इसकी फोकस दूरी होगी –
(a) 20 सें० मी०
(b) 40 सें० मी०
(c) 10 सें० मी०
(d) 50 सें० मी०।
उत्तर-
(d) 50 सें० मी०।

प्रश्न 2.
वस्तु का आभासी और बराबर आकार का प्रतिबिंब बनाता है
(a) अवतल दर्पण
(b) उत्तल दर्पण
(c) समतल दर्पण
(d) इनमें से कोई नहीं।
उत्तर-
(c) समतल दर्पण।

प्रश्न 3.
उत्तल दर्पण द्वारा वस्तु का प्रतिबिंब बनता है, सदैव
(a) वास्तविक, उल्टा व वस्तु से छोटा
(b) आभासी, उल्टा तथा वस्तु से छोटा
(c) आभासी, सीधा तथा वस्तु से छोटा
(d) आभासी, सीधा तथा वस्तु से बड़ा।
उत्तर-
(c) आभासी, सीधा तथा वस्तु से छोटा।

प्रश्न 4.
मोटर वाहन में पीछे का दृश्य देखने के लिए प्रयोग करते हैं –
(a) अवतल दर्पण
(b) समतल दर्पण
(c) उत्तल दर्पण
(d) कोई भी गोलीय दर्पण।
उत्तर-
(c) उत्तल दर्पण।

प्रश्न 5.
Sini/Sinr में सम्बन्ध प्रतिपादित किया –
(a) न्यूटन ने
(b) रमन ने
(c) स्नैल ने
(d) फैराडे ने।
उत्तर-
(c) स्नैल ने।

प्रश्न 6.
किसी लैंस की फोकस दूरी निम्नलिखित में से किस सूत्र द्वारा व्यक्त की जाती है ?
(a) \(\frac{1}{f}=\frac{1}{v}+\frac{1}{u}\)
(b) \(\frac{1}{f}=\frac{1}{v}-\frac{1}{u}\)
(c) f\(=\frac{1}{v}=\frac{1}{u}\)
(d) \(\frac{1}{f}=\frac{1}{u}-\frac{1}{v}\)
उत्तर-
(b) \(\frac{1}{f}=\frac{1}{v}-\frac{1}{u}\)

प्रश्न 7. अवतल दर्पण की वक्रता त्रिज्या R तथा फोकस दूरी के बीच सम्बन्ध होता है
(a) f= R
(b) f= R/2
(c) R = f/2
(d) R = f/4.
उत्तर-
(b) f = R/2.

प्रश्न 8.
एक अवतल दर्पण के वक्रता केंद्र पर स्थापित वस्तु का वास्तविक तथा उल्टा प्रतिबिंब कहाँ बनेगा ?
(a) F पर
(b) C पर
(c) C तथा F के बीच
(d) अनंत पर।
उत्तर-
(b) C पर।

प्रश्न 9.
दंत चिकित्सक द्वारा प्रायः उपयोग में लाए जाने वाला दर्पण –
(a) उत्तल दर्पण
(b) अवतल दर्पण
(c) उत्तल और अवतल दर्पण
(d) समतल दर्पण।
उत्तर-
(b) अवतल दर्पण।

प्रश्न 10.
बड़ा तथा वास्तविक प्रतिबिंब प्राप्त करने के लिए उपयोग होने वाला दर्पण
(a) उत्तल दर्पण
(b) अवतल दर्पण
(c) समतल दर्पण
(d) इनमें से कोई नहीं।
उत्तर-
(b) अवतल दर्पण।

रिक्त स्थानों की पूर्ति कीजिए-

(i) निर्वात में प्रकाश की चाल ……………………… है।
उत्तर-
3 x 10⁸ ms^-1

(ii) प्रकाश ………………………. के कारण पानी में रखा हुआ सिक्का वास्तविक स्थिति से ऊपर उठा हुआ दिखाई देता है।
उत्तर-
अपवर्तन

(iii) समतल दर्पण द्वारा बना प्रतिबिंब सीधा, आभासी और …………………………. होता है।
उत्तर-
वस्तु के बराबर

(iv) कम फोकस दूरी वाले लेंसों की क्षमता अधिक दूरी वाले लेंसों की अपेक्षा ………………………………. होती है।
उत्तर-
अधिक

(v) वस्तु के आकार का प्रतिबिंब प्राप्त करने के लिए वस्तु को उत्तल लैंस के सामने ……………………………… पर रखना चाहिए।
उत्तर-
2F ।

PSEB 10th Class Science Important Questions Chapter 10 प्रकाश-परावर्तन तथा अपवर्तन

Leave a Comment Cancel reply