PSEB 11th Class Chemistry Solutions Chapter 6 Thermodynamics

Punjab State Board PSEB 11th Class Chemistry Book Solutions Chapter 6 Thermodynamics Textbook Exercise Questions and Answers.

PSEB Solutions for Class 11 Chemistry Chapter 6 Thermodynamics

PSEB 11th Class Chemistry Guide Thermodynamics InText Questions and Answers

Question 1.
Choose the correct answer. A thermodynamic state function is a quantity
(i) used to determine heat changes
(ii) whose value is independent of path
(iii) used to determine pressure volume work
(iv) whose value depends on temperature only.
Answer:
(ii) A thermodynamic state function is a quantity whose value is independent of path. Functions like p, V, T etc., depend only on the state of a system and not on the path.

Question 2.
For the process to occur under adiabatic conditions, the correct condition is:
(i) ΔT = 0 (ii) Δp = 0
(iii) q = 0 (iv) w = 0
Answer:
(iii) A system is said to be under adiabatic conditions if there is no exchange of heat between the system and its surroundings. Hence, under adiabatic conditions, q = 0.

Question 3.
The enthalpies of all elements in their standard states are:
(i) unity
(ii) zero
(iii) < 0
(iv) different for each element
Answer:
(ii) The enthalpies of all elements in their standard states are zero.

Question 4.
\(\Delta \boldsymbol{U}^{\ominus}\) of combustion of methane is – X kJ mol^-1. The value of \(\Delta \boldsymbol{H}^{\ominus}\) is
(i) = ΔU
(ii) > ΔU
(iii) \(\Delta \boldsymbol{U}^{\ominus}\)
(iv) = 0
Answer:
(iii) CH₄(g) + 2O₂(g) > CO₂(g) + 2H₂O(l)
Δ_ng = n_p-n_r = 1 – 3 =-2
Hence,\(\Delta \boldsymbol{H}^{\ominus}\) = \(\Delta \boldsymbol{U}^{\ominus}\) + Δ n_gRT
\(\Delta \boldsymbol{H}^{\ominus}\) = – X – 2RT
Hence, \(\Delta \boldsymbol{H}^{\ominus}\) < \(\Delta \boldsymbol{U}^{\ominus}\)

Question 5.
The enthalpy of combustion of methane, graphite and dihydrogen at 298 K are, -890.3 kJ mol^-1 – 393.5 kJ mol^-1 and -285.8 kJ mol^-1 respectively. Enthalpy of formation of CH₄(g) will be
(i) -748kJmol^-1
(ii) -52.27kJ mol^-1
(iii) +748kJ mol^-1
(iv) +52.26kJ mol^-1
Answer:
According to the equation
(i) CH₄(g) + 2O₂(g) → CO₂(g) + 2H₂O(l); ΔH = -890.3 kJ mol^-1

(ii) C(s) + O₂(g) → CO₂(g); ΔH = – 393.5 kJ mol^-1

(iii) H₂(g) + \(\frac{1}{2}\)O₂(g) → H₂O(l); ΔH = -285.8 kJ mol^-1
Multiplying equation (iii) by 2, we get equation (iv).

(iv) 2H₂(g) + O₂(g) → 2H₂O(l); ΔH = – 571.6 kJ mol^-1
Adding eqs. (ii) and (iv), we get

(v) (C(s) +2H₂(g) + 2O₂(g) → CO₂(g) + 2H₂O(l); ΔH = – 965.1 kJ mol^-1
Reversing eqs. (i)

(vi) CO₂(g) + 2H₂O(l) → CH₄(g) + 2O₂(g); ΔH = +890.3 kJ mol^-1
Adding eqs. (v) and (vi), we get
C(s) + 2H₂(g) → CH₄(g); ΔH = – 74.8 kJ mol^-1
Hence, option (i) is correct.

Question 6.
A reaction, A + B → C + D +q is found to have a positive entropy change. The reaction will be
(i) possible at high temperature
(ii) possible only at low temperature
(iii) not possible at any temperature
(iv) possible at any temperature
Answer:
(iv) For a reaction to be spontaneous, AG should be negative.
ΔG = ΔH – TΔS
According to the question, for the given reaction,
ΔS = positive
ΔH = negative (since heat is evolved)
=> ΔG = negative
Therefore, the reaction is spontaneous at any temperature.
Hence, option (iv) is correct.

Question 7.
In a process, 701 J of heat is absorbed by a system and 394 J of work is done by the system. What is the change in internal energy for the process?
Answer:
According to the first law of thermodynamics,
ΔU = q + W …(i)
Given,
q = +701 J (heat is absorbed here, q is positive)
W=- 394 J
(work is done by the system hence W is negative)
Substituting the values in expression (i), we get
ΔU= +701 J + (-394 J)
ΔH = 307 J
Hence, the change in internal energy for the given process is 307 J.

Question 8.
The reaction of cyanamide, NH₂CN(s) with dioxygen was carried out in a bomb calorimeter, and ΔU was found to be – 742.7 kJ mol^-1 at 298K. Calculate enthalpy change for the reaction at 298 K.
NH₂CN(s) + \(\frac{3}{2}\)O₂(g) → N₂(g) + CO₂(g) + H₂O(l)
Answer:
The given reaction is
NH₂CN(s) + \(\frac{3}{2}\)O₂(g) → N₂(g) + CO₂(g) + H₂O(l)
Difference of moles of gaseous products and reactants,
Δ_ng = n_p – n_r = 2 – \(\frac{3}{2}=\frac{1}{2}\) = 0.5 mol
Given, ΔU=- 742.7kJ mol^-1
Enthalpy change ΔH = ΔU + Δ_ngRT
= – 742.7 + (0.5 x 8.314 x 10^-3 x 298)
= – 742.7 +1238.786 x 10^-3
= – 741.46 kJ mol^-1

Question 9.
Calculate the number of kJ of heat necessary to raise the temperature of 60.0 g of aluminium from 35°C to 55°C. Molar heat capacity of Al is 24 J mol^-1K^-1.
Answer:
Given, mass of Al = 60.0 g
ΔT= 55 – 35 = 20°C
No.of moles of Al = \(\frac{60.0}{27}\) mol
Molar heat capacity of Al
= 24 J mol^-1K^-1
Heat, q = n.C . ΔT
= [ \(\frac{60}{27}\) mol )(24 J mol^-1K^-1)(20 K)
q= 1066.7 J
q = 1.07 kJ

Question 10.
Calculate the enthalpy change on freezing of 1.0 mol of water at 10.0°C to ice at – 10.0°C. Δ_fusH = 6.03 kJ mol^-1 at 0°C.
C_p[H₂O(l)] – 75.3 J mol^-1K^-1
C_p[H₂O(s)] = 36.8J mol^-1K^-1
Answer:
(i) Heat change required to lower the temperature of water from 10.0°Cto0°C
ΔH₁= n x C_p x ΔT= 1.0 x 75.3 x (-10) = – 753 J mol^-1
(ii) Heat change required to convert 1 mol of H₂O(l) at 0°C to H₂O(s) at 0°C
ΔH₂ = ΔH_fusion = – 6.03 kJ mol^-1 as heat is given out
(iii) Heat change required to change 1 mole of ice from 0°C to -10.0° C
ΔH₃ = – 36.8 x 10 x 1 = – 368 J mol^-1
Total heat change
= ΔH₁ + ΔH₂ + ΔH₃ = (- 0.753 – 6.03 – 0.368) kJ mol^-1
∴ Total enthalpy change = – 7.151 kJ mol^-1
As in each step, heat is evolved, each step will have a negative sign with Δ_H

Question 11.
Enthalpy of combustion of carbon to CO₂ is -393,5 kJ mol^-1. Calculate the heat released upon formation of 35.2 g of CO₂ from carbon and dioxygen gas.
Answer:
The reaction for the combustion of carbon into CO₂ is
C(s) + O₂(g) → CO₂(g); ΔH = – 393.5 kJ mol^-1 (1 mole CO₂ – 44g)
Heat released in the formation of 44 g CO₂ = 393.5 kJ
∴ Heat released in the formation of 35.2 g CO₂
\(\frac{393.5 \mathrm{~kJ}}{44 \mathrm{~g}}\) x 5.2g = 314.8 kJ mol^-1

Question 12.
Enthalpies of formation of CO(g), CO₍₂₎(g), N₂O(g) and N₂O₄(g) are -110, -393, 81and 9.7 kJ mol^-1 respectively. Find the value of Δ_rH for the reaction:
N₂O₄(g) + 3CO(g) → N₂O(g) + 3CO₂(g)
Answer:
Δ_fH (CO) = -110 kJ mol^-1
ΔH_f(CO₂) = -393 kJ mol^-1
Δ_fH (N₂O)= 81 kJ mol^-1
Δ_fH (N₂O₄) = 9.7 kJ mol^-1
The given reaction is
N₂O₄(g) + 3CO(g) → N₂O(g) + 3CO₂(g); Δ_rH = ?

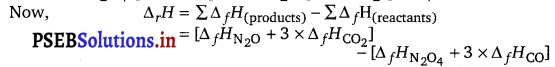
= [81 + 3 (-393)] – [9.7 + 3 (-110)] kJ = [81 -1179]-[9.7-330] kJ
Δ_rH = – 777.8 kJ.

Question 13.
Given : N₂(g) + 3H₂(g) → 2NH₃(g); \(\Delta_{\boldsymbol{r}} \boldsymbol{H}^{\ominus}\) = -92.4kJ mol^-1.
What is the standard enthalpy of formation of NH₃ gas?
Answer:
Given, N₂(g) + 3H₂(g) → 2NH₃(g); Δ_rH = – 92.4 kJ mol^-1
Chemical reaction for the enthalpy of formation of NH3(g) is as follows :
\(\frac{1}{2}\)N₂(g) + \(\frac{3}{2}\)H₂(g) → NH₃(g)
∴ Standard enthalpy of formation of NH₃(g)
= \(\frac{1}{2}\)\(\Delta H^{\theta}\) = \(\frac{1}{2}\) (-92.4 kJ mol^-1) = -46.2 kJ mol^-1

Question 14.
Calculate the standard enthalpy of formation of CH₃OH(l) from the following data:
CH₃OH(l) + \(\frac{3}{2}\)O₂(g) → CO₂(g) + 2H₂O(l); \(\Delta_{\boldsymbol{r}} \boldsymbol{H}^{\ominus}\) = -726 kJ mol^-1
C_(graphite) + O₂(g) → CO₂(g); \(\Delta_{\boldsymbol{c}} \boldsymbol{H}^{\ominus}\) = – 393 kJ mol^-1
H₂(g) + \(\frac{1}{2}\)O₂(g) → H₂O(l); \(\Delta_{\boldsymbol{f}} \boldsymbol{H}^{\ominus}\) = – 286 kJ mol^-1
Answer:

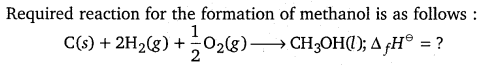
Question 15.
Calculate the enthalpy change for the process
CCl₄(g) → C(g) + 4Cl(g)
and calculate bond enthalpy of C—Cl in CCl₄(g).
\(\Delta_{\mathbf{v a p}} \boldsymbol{H}^{\ominus}\)(CCl₄) = 30.5kJ mol^-1. \(\Delta_{\boldsymbol{f}} \boldsymbol{H}^{\ominus}\)(CCl₄) = – 135.5kJ mol^-1.
\(\Delta_{a} \boldsymbol{H}^{\ominus}(\mathbf{C})\) = 715.0kJ mol^-1, \(\Delta_{\boldsymbol{a}} \boldsymbol{H}^{\ominus}\left(\mathbf{C l}_{\mathbf{2}}\right)\)(Cl2) = 242 kJ mol^-1; where \(\Delta_{\boldsymbol{a}} \boldsymbol{H}^{\ominus}\) is enthalpy of atomisation.
Answer:
Given,
(i) CCl₄(Z) → CCl₄(g); \(\Delta_{\mathrm{vap}} H^{\ominus}\) = +30.5 kJ mol^-1
(ii) C(s) → C(g); \(\Delta_{a} H^{\ominus}\) = 715.0 kJ mol^-1
(iii) Cl₂(g) → 2Cl(g); \(\Delta_{a} H^{\ominus}\) = 242 kJ mol^-1
(iv) C(s) + 2Cl₂(g) → CCl₄ a); \(\Delta_{f} H^{\ominus}\) = – 135.5KJ mol^-1

Enthalpy change for the given process
CCl₄(g) → C(g) + 4Cl(g); \(\Delta_{r} H^{\ominus}\) = ?

Add (i) and (iv) and subtract (ii) and (iii) x 2
CCl₄(l) + C(s) + 2Cl₂(g) – C(s) – 2Cl₂ (g) → CCl₄(g) + CCl₄(g) – C(g) – 4Cl(g)
or \(\Delta_{r} H^{\ominus}\) = 30.5 -135.5 – 715 – 484 = -1304 kJ
0 = CCl₄(g) – C(g) + 4Cl(g); \(\Delta_{r} H^{\ominus}\) = -1304kJ
CCl₄(g) → C (g) + 4Cl(g); \(\Delta_{r} H^{\ominus}\) = 1304 kJ
There are four bonds of C—Cl in CCl₄.
Bond enthalpy of C—Cl bond
= \(\frac{1304}{4}\) mol^-1
= 326 kJmol^-1

Question 16.
For an isolated system, ΔU = 0, what will be ΔS ?
Ans. For an isolated system, ΔU = 0 and for a spontaneous process, total entropy change must be positive. For example, consider the diffusion of two gases A and B into each other in a closed container which is isolated from the surroundings.

The two gases A and B are separated by a movable partition. When partition is removed, the gases begin to diffuse into each other and the system becomes more disordered. It shows that ΔS > 0 and ΔU = 0 for this process.
Moreover, ΔS =\(=\frac{q_{\mathrm{rev}}}{T}=\frac{\Delta H}{T}=\frac{\Delta U+p \Delta V}{T}=\frac{p \Delta V}{T}\) (∴ ΔU = 0)
i.e., TΔS or ΔS > 0

Question 17.
For the reaction at 298 K, 2A + B > C
ΔH = 400kJ mol^-1 and ΔS = 0.2kJK^-1mol^-1 At what temperature will the reaction become spontaneous considering ΔH and ΔS to be constant over the temperature range?
Answer:
Given, ΔH = 400 kJ mol^-1, ΔS = 0.2 kJ K^-1mol^-1
Gibbs free energy, ΔG = ΔH – TΔS
0 = 400 kJ mol^-1 – T x 0.2 kJ K^-1mol^-1
(ΔG = 0 at equilibrium)
T = \(\frac{400 \mathrm{~kJ} \mathrm{~mol}^{-1}}{0.2 \mathrm{~kJ} \mathrm{~K}^{-1} \mathrm{~mol}^{-1}}\)
T = 2000 K
For the reaction to be spontaneous, ΔG must be negative. Hence, for the given reaction to be spontaneous, T should be greater than 2000 K.

Question 18.
For the reaction,
2Cl(g) → Cl₂(g), what are the signs of ΔH and ΔS?
Answer:
ΔH and ΔS are negative.
The given reaction represents the formation of chlorine molecule from chlorine atoms. Here, bond formation is taking place. Therefore, energy is being released. Hence, ΔH is negative.
Also, two moles of atoms have more randomness than one mole of a molecule. Since spontaneity is decreased, ΔS is negative for the given reaction.

Question 19.
For the reaction : 2A(g) + B(g) → 2D(g)
\(\Delta \boldsymbol{U}^{\ominus}\) = – 10.5 kJ and ΔS = – 441 JK^-1.
Calculate \(\Delta \boldsymbol{G}^{\ominus}\) for the reaction, and predict whether the reaction may occur spontaneously.
Answer:
For the given reaction,
2A(g) + B(g) → 2D(g)
Δn_g = 2 – 3 = -1 mol
Substituting the value of \(\Delta \boldsymbol{U}^{\ominus}\) in the expression ofΔH
\(\Delta H^{\ominus}=\Delta U^{\ominus}+\Delta n_{g} R T\)
= (-10.5 kJ) + (-1) x (8.314 x 10^-3kJK^-1 mol^-1) x (298 K)
= -10.5 kJ-2.48 kJ
\(\Delta H^{\ominus}\) = -12.98 kJ
We know that,
\(\Delta G^{\ominus}=\Delta H^{\ominus}-T \Delta S^{\ominus}\)
= -12.98 kJ – (298K) x ( – 44.1 JK^-1)
= -12.98 kJ + 13.14kJ
\(\Delta G^{\ominus}\) = +0.16 kJ
Since, \(\Delta G^{\ominus}\) is positive, the reaction will not occur spontaneously.

Question 20.
The equilibrium constant for a reaction is 10. What will be the value of \(\Delta G^{\ominus}\)? R = 8.314 JK^-1mol^-1, T = 300 K.
Answer:
\(\Delta G^{\ominus}\) = – 2303RT log K_c
Given, K_c = 10, T = 300 K, R = 8.314 J K^-1 mol^-1
\(\Delta G^{\ominus}\) = (- 2.303) (8.314 JK^-1mol^-1) (300K) (loglO) (∵ log 10 = 1)
= – 5744.14 Jmol^-1 = – 5.744 kJmol^-1

Question 21.
Comment on the thermodynamic stability of NO(g), given
\(\frac{1}{2}\)N₂(g) + \(\frac{1}{2}\)O₂(g) → NO(g); \(\Delta_{\boldsymbol{r}} \boldsymbol{H}^{\ominus}\) = 90 kJ mol^-1
NO(g) + \(\frac{1}{2}\)O₂(g) → NO₂(g); \(\Delta_{\boldsymbol{r}} \boldsymbol{H}^{\ominus}\) = – 74 kJ mol^-1
Answer:
NO(g) is unstable because formation of NO is endothermic (energy is absorbed) but NO₂(g) is formed because its formation is exothermic (energy is released).
Hence, unstable NO(g) changes to stable NO₂(g).

Question 22.
Calculate the entropy change in surroundings when 1.00 mol of H₂O(Z) is formed under standard conditions. \(\Delta_{\boldsymbol{f}} \boldsymbol{H}^{\ominus}\) = – 286
kJ mol^-1.
Answer:
Enthalpy change for the formation of 1 mol of H₂O(Z)
H₂(g) + \(\frac{1}{2}\)O₂(g) → H₂O(l); \(\Delta_{f} H^{\mathrm{s}}\) = -286 kJ mol^-1
Energy released in the above reaction is absorbed by the surroundings. * It means,
q_surr = + 286 kJ mol^-1
Entropy change ΔS_surr = \(=\frac{q_{\mathrm{surr}}}{T}=\frac{286 \mathrm{~kJ} \mathrm{~mol}^{-1}}{298 \mathrm{~K}}\)
ΔS_surr = 0.95973 kJ K^-1 mol^-1 = 959.73 J mol^-1K^-1