PSEB 11th Class Economics Solutions Chapter 19 बिन्दु रेखीय प्रस्तुतीकरण

Punjab State Board PSEB 11th Class Economics Book Solutions Chapter 19 बिन्दु रेखीय प्रस्तुतीकरण Textbook Exercise Questions, and Answers.

PSEB Solutions for Class 11 Economics Chapter 19 बिन्दु रेखीय प्रस्तुतीकरण

PSEB 11th Class Economics बिन्दु रेखीय प्रस्तुतीकरण Textbook Questions and Answers

I. वस्तुनिष्ठ प्रश्न (Objective Type Questions)

प्रश्न 1.
चित्रों द्वारा प्रस्तुतीकरण का एक लाभ लिखें।
उत्तर-
चित्रों की सहायता से जटिल-से-जटिल आंकड़ों को सरल, साधारण एवं समझने योग्य बनाया जा सकता है। इनको देखते ही आंकड़ों की विशेषताएं समझ में आ जाती हैं।

प्रश्न 2.
चित्रों द्वारा प्रस्तुतीकरण की एक सीमा लिखिए।
उत्तर-
चित्रों द्वारा आंकड़ों के प्रस्तुतीकरण से केवल अनुमान (Estimate) लगाया जा सकता है। इसके द्वारा पूर्ण ज्ञान नहीं हो सकता। इसके विपरीत सारणी द्वारा समस्या का पूर्ण ज्ञान प्राप्त किया जा सकता है।

प्रश्न 3.
दण्ड चित्र (Bar Diagram) किसे कहते हैं ?
उत्तर-
दण्ड चित्र वह चित्र है जिसमें आंकड़ों को दण्डों (Bars) या आयतों के रूप में प्रकट किया जाता है।

प्रश्न 4.
वृत्तीय चित्र किसे कहते हैं?
उत्तर-
वृत्तीय चित्र वह चित्र है जिसमें एक वृत्त (Circle) को कई भागों में बांट कर किसी आंकड़े के भिन्न-भिन्न प्रतिशत या सापेक्ष मूल्यों को प्रस्तुत किया जाता है। वृत्तीय चित्रों का प्रयोग प्रतिशतों के आधार पर किया जाता है।

प्रश्न 5.
बहुगुणी दण्ड चित्र (Multiple Bar Diagram) किसे कहते हैं?
उत्तर-
बहुगुणी दण्ड चित्र वह दण्ड चित्र हैं जो दो या दो से अधिक तथ्यों के आंकड़ों को प्रस्तुत करता है। इनका प्रयोग विभिन्न तथ्यों जैसे जन्म-दर तथा मृत्यु-दर की तुलना के लिए किया जाता है।

प्रश्न 6.
सरल दण्ड चित्र किसे कहते हैं?
उत्तर-
सरल दण्ड चित्र वे चित्र हैं जो एक ही प्रकार के संख्यात्मक तथ्यों के विभिन्न मूल्यों को दण्डों के द्वारा प्रकट करते हैं।

प्रश्न 7.
जब आंकड़ों को दण्डों के रूप में प्रकट किया जाता है तो इसको ………………… कहते हैं।
(a) दण्ड चित्र
(b) बहुदण्ड चित्र
(c) रेखाचित्र
(d) इनमें से कोई नहीं।
उत्तर-
(a) दण्ड चित्र।

प्रश्न 8.
जब किसी तथ्य के विभिन्न भागों को प्रतिशत के रूप में प्रकट किया जाता है तो इसको ………. चित्र कहते हैं।
उत्तर-
प्रतिशत।

प्रश्न 9.
गोलाकार चित्र को …………… चित्र भी कहा जाता है।
उत्तर-
पाई।

प्रश्न 10.
दो अथवा दो से अधिक तथ्यों वाले चित्र को बहुदण्ड चित्र कहा जाता है।
उत्तर-
सही।

प्रश्न 11.
मानचित्र को रेखाचित्र भी कहा जाता है।
उत्तर-
ग़लत।

प्रश्न 12.
एक से अधिक तथ्यों वाले समूह और भागों के रूप में प्रकट करते हैं तो इस को ……………….. कहते हैं।
(a) दण्ड चित्र
(b) बहुदण्ड चित्र
(c) मानचित्र
(d) उप विभाजित दण्ड चित्र।
उत्तर-
(d) उप विभाजित दण्ड चित्र।

प्रश्न 13.
जब तस्वीर बना कर आंकड़ों को पेश किया जाता है तो इसको पाई चित्र कहते हैं।
उत्तर-
ग़लत।

प्रश्न 14.
आंकड़ों को चित्रों द्वारा स्पष्ट करने को …………… कहते हैं।
(a) सारणीयन
(b) वर्गीकरण
(c) व्यवस्थीकरण
(d) इनमें से कोई नहीं।
उत्तर-
(d) इनमें से कोई नहीं।

प्रश्न 15.
दण्ड से क्या अभिप्राय है ?
उत्तर-
दण्ड से अभिप्राय एक आयत अथवा आयतकार चित्र से है जिस द्वारा किसी चर के मूल्य प्रकट किये जाते हैं।

प्रश्न 16.
दण्ड चित्र दो प्रकार के होते हैं ?
उत्तर-
सही।

प्रश्न 17.
जो चित्र दो अथवा दो से अधिक तथ्यों को प्रकट करते हैं उनको ………. चित्र कहते हैं।
उत्तर-
बहुगुणी चित्र।

प्रश्न 18.
दण्ड चित्र का कोई एक लाभ बताएँ।
उत्तर-
दण्ड चित्र द्वारा आंकड़ों को आकर्षक (दिलकश) बनाया जा सकता है।

प्रश्न 19.
एक चित्र में दो से अधिक चरों को प्रकट किया जाता है तो इसको बहुगुणी चित्र कहा जाता है।
उत्तर-
सही।

II. अति लघु उत्तरीय प्रश्न (Very Short Answer Type Questions)

प्रश्न 1.
चित्रों द्वारा प्रस्तुतीकरण के अर्थ बताएं।
उत्तर-
चित्रों द्वारा प्रस्तुतीकरण का अर्थ-आंकड़ों को रोचक तथा सरल बनाने के लिए आंकड़ा शास्त्रियों ने विभिन्न विधियों का प्रयोग किया है। इनमें से एक विधि आंकड़ों का चित्रों द्वारा प्रस्तुतीकरण होता है। आंकड़ों का चित्रों द्वारा प्रस्तुतीकरण वह विधि होती है, जिसमें आंकड़ों को डण्डा चित्र (Bar Diagrams), आयत (Rectangels), चतुर्भुज (Squares), पाई चित्र (Pie Diagrams), तस्वीरें (Pictograms), मानचित्रण (Artograms) इत्यादि के रूप में पेश किया जाता है। चाहे वर्गीकरण तथा सूचीकरण से काफ़ी हद तक आंकड़ों में सरलता आ जाती है, परन्तु इन आंकड़ों को रोचक तथा मनमोहक बनाने के लिए चित्रों द्वारा प्रदर्शन आवश्यक होता है। इसको स्पष्ट करते हुए प्रो० एस० जे० मेरोनी ने ठीक कहा है, “ठण्डे आंकड़े बहुत-से लोगों को गैर-उत्साहजनक होते हैं। जटिल स्थितियों को सरल तथा नियमित रूप देने के लिए चित्र सहायक होते हैं।”

प्रश्न 2.
चित्रों द्वारा प्रस्तुतीकरण के कोई दो लाभ बताएँ।
उत्तर-

1. रोचक बनाना (Attractive)-चित्रों की सहायता से आंकड़ों को रोचक बनाया जा सकता है। हम जानते हैं कि साधारण मनुष्य आंकड़ों में रुचि नहीं लेते, इसलिए चित्र बनाकर उन मनुष्यों को आंकड़ों का ज्ञान दिया जा सकता है।
2. तुलना में आसानी (Easy Comparison)-चित्र आंकड़ों की तुलना में बहुत सहायता करते हैं, जैसे कि किसी देश में जनसंख्या की वृद्धि की तुलना समय के आधार पर चित्रों द्वारा की जा सकती है। इसी तरह कीमतों की वृद्धि को सूचकांक के चित्र द्वारा स्पष्ट किया जा सकता है।

प्रश्न 3.
चित्रों द्वारा प्रस्तुतीकरण की कोई दो सीमाएं बताएं।
उत्तर-

1. ग़लत व्याख्या (Wrong Interpretation)- चित्रों द्वारा तथ्यों की ठीक व्याख्या नहीं की जा सकती। यह तो आंकड़ों को प्रदशित करने का एक साधन मात्र होता है। कई बार चित्रों को देखकर पाठक गलत परिणाम निकाल लेते हैं।
2. सीमित सूचना (Limited Information)-विशाल आंकड़ों को चित्रों द्वारा प्रदर्शित किया जाता है तो वास्तविक सूचना प्रदान नहीं की जा सकती। इस उद्देश्य की पूर्ति के लिए थोड़ी सूचना प्रदान की जाती है। परिणामस्वरूप आंकड़ों को पेश करने का उद्देश्य समाप्त हो जाता है।

प्रश्न 4.
चक्र अथवा पाई चित्र से क्या अभिप्राय है ?
उत्तर-
चक्र अथवा पाई चित्र (Pie Diagram)-चित्र को गोलाकार रूप में भी स्पष्ट किया जाता है। इस स्थिति में एक गोल चक्कर का निर्माण करने के पश्चात् इसमें 36° कोणों का योग होता है। इसलिए प्रत्येक मूल्य को स्पष्ट करते समय इसका मूल्य 360° के अनुपात में प्राप्त किया जाता है तथा जब हमारे पास प्रत्येक मूल्य का योगदान डिग्री के रूप में प्राप्त हो जाता है तो उस अनुसार हम गोलाकार चित्र का निर्माण करते हैं।

प्रश्न 5.
चित्र लेख से क्या अभिप्राय है ?
उत्तर-
चित्र लेख (Pictograph)-चित्र लेख वह विधि होती है, जिस द्वारा तस्वीरों को बनाकर आंकड़ों का प्रदर्शन करने का प्रयत्न किया जाता है। उदाहरणस्वरूप एक देश की जनसंख्या को 1951 तथा 1991 के समय का तुलनात्मक अध्ययन करना है तो इस स्थिति में देश X की जनसंख्या के आंकड़े इस प्रकार दिए गए हैं-
(Population of A Country) देश X की जनसंख्या
1951-4 करोड़
1991-7 करोड़

III. लघु उत्तरीय प्रश्न (Short Answer Type Questions)

प्रश्न 1.
दण्ड चित्र को कितने भागों में विभाजित किया जा सकता है ? स्पष्ट करो। दण्ड चित्र के निर्माण को भी स्पष्ट करो।
उत्तर-
दण्ड अथवा डण्डा चित्र-दण्ड चित्र वह चित्र होता है, जिसमें आंकड़ों को डंडे (Bars) अथवा आयतों के रूप में स्पष्ट किया जाता है। दण्ड चित्र का निर्माण इस प्रकार किया जाता है-

1. डण्डा शब्द का प्रयोग आयत के लिए किया जाता है। चित्र में डण्डों की चौड़ाई समान रखनी चाहिए।
2. डण्डे लंब रूप में अथवा लेटवें रूप में हो सकते हैं।
3. यह डण्डे समान दूरी पर बनाने चाहिए।
4. डण्डे बनाने का आधार (Base) एक होना चाहिए।

दण्ड चित्र अथवा डण्डा चित्र के रूप-दण्ड चित्र को एक पक्षीय चित्र (One dimensional diagram) भी कहा जाता है। यह मुख्य तौर पर निम्नलिखित रूप में बनाए जा सकते हैं-

1. सरल डण्डा चित्र-सरल डण्डा चित्र वह चित्र है, जिसमें संख्याओं को विभिन्न मूल्यों के डण्डों द्वारा प्रकट किया जाता है।
2. बहुगुणी डण्डा चित्र-बहुगुणी डण्डा चित्र वह चित्र है, जिनमें दो या दो से अधिक गुणों को प्रकट किया जाता है।
3. उपविभाजित डण्डा चित्र-उपविभाजित डण्डा चित्र वह चित्र होते हैं, जो किसी तथ्य के कुल मूल्य के साथ इसके भागों को भी पेश करते हैं।
4. प्रतिशत डण्डा चित्र-प्रतिशत डण्डा चित्र वह चित्र होते हैं, जिसमें किसी तथ्य के विभिन्न मूल्यों को प्रतिशत के रूप में दिखाया जाता है।

प्रश्न 2.
निम्नलिखित आंकड़ों के आधार तथा सरल दण्ड चित्र का निर्माण करो। वर्ष

वर्ष	1951	1961	1971	1981	1991	2001
भारत की जनसंख्या (करोड़ों में)	36	43	54	68	84	102

उत्तर-
सरल दण्ड चित्र ऐसा चित्र होता है, जिसमें एक गुण की व्याख्या ही की जाती है, जैसे कि जनसंख्या उत्पादन बिक्री, लाभ इत्यादि गुण को दिखाया जाए तो ऐसे चित्र को सरल दण्ड चित्र कहा जाता है। उदाहरणस्वरूप भारत की जनसंख्या के आंकड़े इस प्रकार दिए गए हैं।

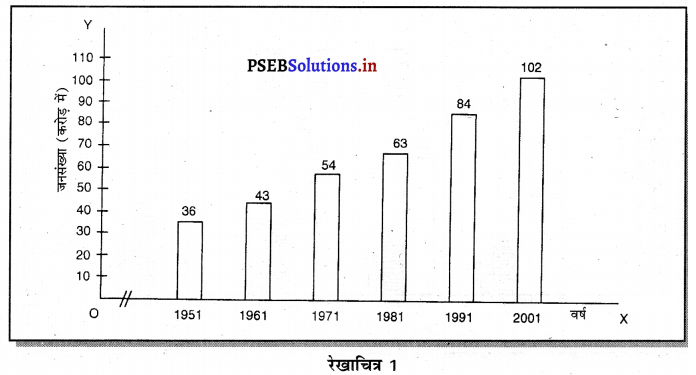
इस चित्र को सरल अथवा साधारण दण्ड चित्र (Simple Bar Diagram) कहा जाता है। इसको लंबवत डण्डा चित्र (Vertical Bar Diagram) भी कहते हैं।

प्रश्न 3.
बहुगुणी डण्डा चित्र से क्या अभिप्राय है ? निम्नलिखित आंकड़ों की सहायता से बहुगुणी डण्डा चित्र का निर्माण करो।

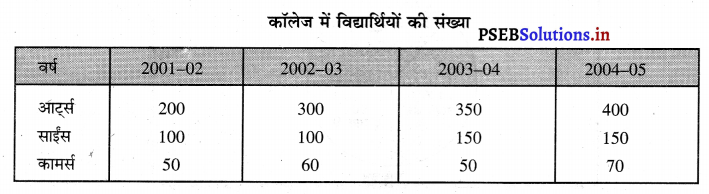
उत्तर-
बहुगुणी डण्डा चित्र (Multiple Bar Diagram)-बहुगुणी डण्डा चित्र वह चित्र होते हैं जो दो अथवा दो से अधिक तथ्यों के आंकड़ों को पेश करते हैं, इनका प्रयोग विभिन्न तथ्यों जैसे कि जन्म दर, मृत्यु दर, आयात-निर्यात, लाभ-हानि, कॉलेज में आर्ट्स, साईंस पढ़ने वाले विद्यार्थियों की संख्या के रूप में पेश की जाती हैं। एक कालेज में आर्ट्स तथा साईंस के धिार्थियों का विवरण इस प्रकार दिया गया है-

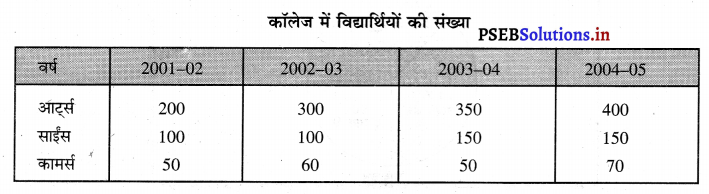
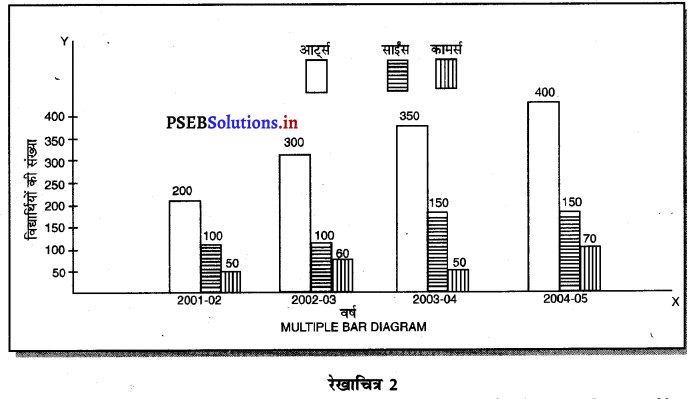
प्रश्न 4.
निम्नलिखित राष्ट्रीय आय में विभिन्न क्षेत्रों का भाग दिखाया गया है। गोल चक्करी तथा पाई रेखा चित्र बनाओ। क्षेत्र

हल : राष्ट्रीय आय के आंकड़े प्रतिशत में दिए गए हैं। इनको 360° में परिवर्तित करके पाई चित्र बनाया जाएगा।

IV. दीर्घ उत्तरीय प्रश्न (Long Answer Type Questions)

प्रश्न 1.
चित्रों द्वारा प्रस्तुतीकरण से क्या अभिप्राय है ? इसके लाभ तथा सीमाएं बताओ।
(What is the meaning of Diagrammatic Presentation ? Discuss its Advantages and limitations.)
उत्तर-
चित्रों द्वारा प्रस्तुतीकरण का अर्थ-आंकड़ों को रोचक तथा सरल बनाने के लिए आंकड़ा शास्त्रियों ने विभिन्न विधियों का प्रयोग किया है। इनमें से एक विधि आंकड़ों का चित्रों द्वारा प्रस्तुतीकरण होता है। आंकड़ों का चित्रों द्वारा प्रस्तुतीकरण वह विधि होती है, जिसमें आंकड़ों को डण्डा चित्र (Bar Diagrams), आयत (Rectangles), चतुर्भुज (Squares), पाई चित्र (Pie Diagrams), तस्वीरें (Pictograms), मानचित्रण (Artograms) इत्यादि के रूप में पेश किया जाता है। चाहे वर्गीकरण तथा सूचीकरण से काफ़ी हद तक आंकड़ों में सरलता आ जाती है, परन्तु इन आंकड़ों को रोचक तथा मनमोहक बनाने के लिए चित्रों द्वारा प्रदर्शन आवश्यक होता है। इसको स्पष्ट करते हुए प्रो० एस० जे० मोरोनी ने ठीक कहा है, “ठण्डे आंकड़े बहुत-से लोगों को गैर-उत्साहजनक होते हैं। जटिल स्थितियों को सरल तथा नियमित रूप देने के लिए चित्र सहायक होते हैं।”

चित्रों के लाभ अथवा महत्त्व (Importance or Advantages of Diagrams) चित्रों द्वारा आंकड़ों को प्रदर्शित करने के बहुत-से लाभ होते हैं, जिनकी व्याख्या इस प्रकार की जा सकती है-

1. सरल तथा समझने योग्य बनाना (Simple and Understandable)-आंकड़ों को सरल तथा समझने योग्य बनाने के लिए चित्र महत्त्वपूर्ण योगदान डालते हैं।
2. रोचक बनाना (Attractive)-चित्रों की सहायता से आंकड़ों को रोचक बनाया जा सकता है। हम जानते हैं कि साधारण मनुष्य आंकड़ों में रुचि नहीं लेते, इसलिए चित्र बनाकर उन मनुष्यों को आंकड़ों का ज्ञान दिया जा सकता है।
3. तुलना में आसानी (Easy Comparison)-चित्र आंकड़ों की तुलना में बहुत सहायता करते हैं, जैसे कि किसी देश में जनसंख्या की वृद्धि की तुलना समय के आधार पर चित्रों द्वारा की जा सकती है। इसी तरह कीमतों की वृद्धि को सूचकांक के चित्र द्वारा स्पष्ट किया जा सकता है।
4. विश्लेषण में आसानी (Easy Interpretation) चित्रों की सहायता से जो परिणाम निकाले जाते हैं, उनके सम्बन्धी जानकारी आसानी से प्राप्त हो जाती है, जैसे कि जनसंख्या में वृद्धि को चित्र द्वारा स्पष्ट किया जाए तो आसानी से पता चल जाता है कि स्वतन्त्रता के पश्चात् अब तक जनसंख्या लगभग तीन गुणा बढ़ गई है।
5. याद करने में आसानी (Easy Memorizing) चित्रों द्वारा तथ्यों को याद करना आसान होता है। आंकड़ों के रूप में इनको लम्बे समय तक याद रखने में मुश्किल का सामना करना पड़ता है। चित्र के रूप में देखे गए आंकड़े जल्दी याद हो जाते हैं।
6. किफायती (Economical)-चित्रों द्वारा समय तथा परिश्रम बहुत कम लगता है। इस विधि द्वारा कम स्थान पर बहुत ज्यादा सूचना कम समय में प्रदान की जा सकती है, जैसे कि एक डॉक्टर मरीज की हालत को चारट देख कर जल्दी दवाई दे देता है।
7. संक्षेप रूप देना (Condensation)-चित्रों द्वारा आंकड़ों को संक्षेप रूप दिया जाता है। इसलिए पुरानी कहावत ठीक है कि तस्वीर हज़ारों शब्दों के बराबर होती है। (A Picture is Worth thousands of Words.)

चित्रों की सीमाएं (Limitations of Diagrams) –
चित्रों द्वारा आंकड़ों के प्रस्तुतीकरण की मुख्य सीमाएं निम्नलिखित अनुसार हैं-

1. गलत व्याख्या (Wrong Interpretation) चित्रों द्वारा तथ्यों की ठीक व्याख्या नहीं की जा सकती। यह तो आंकड़ों को प्रदर्शन करने का एक साधन मात्र होता है। कई बार चित्रों को देखकर पाठक गलत परिणाम निकाल लेते हैं।
2. सीमित सूचना (Limited Information)-विशाल आंकड़ों को चित्रों द्वारा प्रदर्शन किया जाता है तो वास्तविक सूचना प्रदान नहीं की जा सकती। इस उद्देश्य की पूर्ति के लिए थोड़ी सूचना प्रदान की जाती है। परिणामस्वरूप आंकड़ों को पेश करने का उद्देश्य समाप्त हो जाता है।
3. अनुमानित मूल्य (Approximate Value)-चित्रों द्वारा आंकड़ों के पूरे मूल्य नहीं दिखाए जा सकते, बल्कि अनुमानित मूल्यों को ही स्पष्ट किया जाता है। इसलिए आंकड़ों को पूर्ण रूप में स्पष्ट करना मुश्किल हो जाता है।
4. दुरुपयोग (Misuse)-चित्रों द्वारा आंकड़ों को उद्देश्य अनुसार तोड़-मरोड़ कर पेश किया जाता है। इसलिए इश्तिहारबाज़ी में इनके भिन्न अर्थ प्रकट किए जाते हैं तथा ग्राहकों को कम उपयोगी वस्तुएं खरीदने के लिए प्रेरणा दी जा सकती है।

प्रश्न 2.
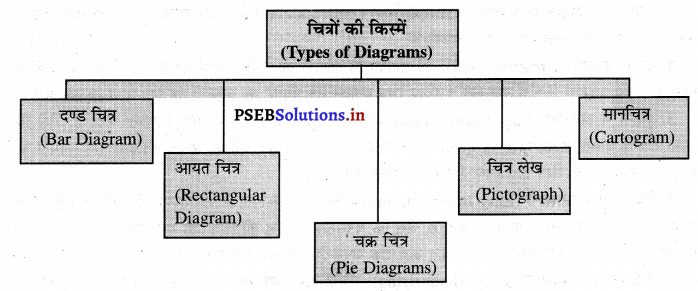
चित्र कितने प्रकार के होते हैं ? इन प्रकारों को स्पष्ट करें। (What are the types of diagrams ? Explain the meanings of the types of diagrams.)
उत्तर-
चित्रों को मुख्य तौर पर पांच भागों में विभाजित कर स्पष्ट किया जाता है। इसलिए चित्रों की 5 किस्में होती हैं, जिनको हम निम्नलिखित खाके की सहायता से स्पष्ट करते हैं-

1. दण्ड चित्र (Bar Diagrams)-रेखाचित्रों को दण्ड चित्र अथवा डण्डा चित्र (Bar Diagrams) के रूप में प्रकट किया जा सकता है। आंकड़ों को पेश करने के लिए चित्रों की यह किस्म बहुत अधिक प्रयोग की जाती है। इस उद्देश्य के लिए सीधी रेखाओं जिनको साधारण डण्डा चित्र (Simple Bar Diagrams) अथवा बहु-डण्डा चित्र (Multiple Bar Diagrams) इत्यादि के रूप में प्रकट किया जाता है। जब हम चित्र के एक ओर अर्थात् ऊपर, नीचे, दाएं अथवा बाईं ओर डण्डे बनाते हैं तो इसको एक पक्षीय (One Dimensional) चित्र कहा जाता है। इसको दण्ड चित्र 4 द्वारा स्पष्ट किया जा सकता है।
उदाहरण-
निम्नलिखित सारणी को डण्डा चित्र की सहायता से स्पष्ट करो।

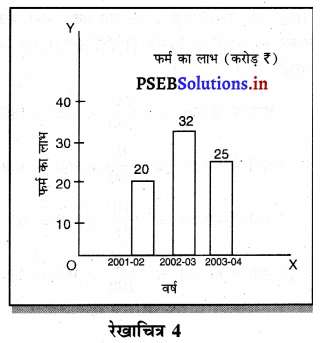
2. आयत चित्र (Rectangular Diagram)-चित्रों को स्पष्ट करने के लिए आयत (Rectangle) तथा वर्ग (Square) का प्रयोग भी किया जाता है। जब हम दो विस्तार वाले चित्रों में चित्र की लम्बाई तथा चौड़ाई दोनों को ही महत्त्व देना चाहते हैं तो ऐसे चित्रों को विस्तार (Two Dimensional) वाले चित्र कहा जाता है। ऐसे चित्रों में चित्रों का क्षेत्रफल महत्त्वपूर्ण होता है जोकि लम्बाई तथा चौड़ाई को गुणा करके प्राप्त किया जाता है। इसलिए आयताकार तथा वर्गाकार चित्रों को छोटे-छोटे भागों में विभाजित कर बहुत-से तथ्यों की भी व्याख्या की जा सकती है। उदाहरणस्वरूप दो फ़र्मों के व्यय तथा लाभ की जानकारी इस प्रकार दी गई है। इसको आयत चित्र द्वारा प्रस्तुत किया जा सकता है – उदाहरण-फ़र्म A तथा फ़र्म B के व्यय पर लाभ का विवरण निम्नलिखित अनुसार है –

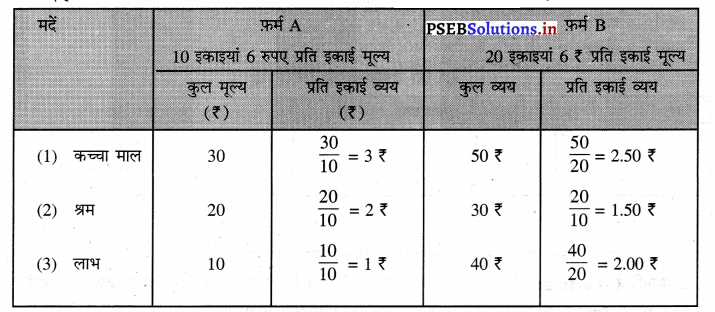
इस प्रकार आयताकार चित्र फ़र्म A तथा B फ़र्म के व्यय, आय, लाभ इत्यादि की जानकारी प्रदान करते हैं।

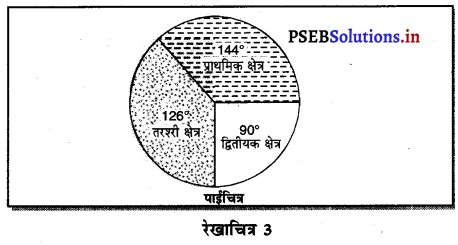
3. चक्र अथवा पाई चित्र (Pie Diagram)-चित्र को गोलाकार रूप में भी स्पष्ट किया जाता है। इस स्थिति में एक गोल चक्कर का निर्माण करने के पश्चात् इसमें 36° कोणों का योग होता है। इसलिए प्रत्येक मूल्य को स्पष्ट करते समय इसका मूल्य 360° के अनुपात में प्राप्त किया जाता है तथा जब हमारे पास प्रत्येक मूल्य का योगदान डिग्री के रूप में प्राप्त हो जाता है तो उस अनुसार हम गोलाकार चित्र का निर्माण करते हैं। इस विधि को डॉक्टर ऊटा न्यूरैथ ने विकसित किया था। उदाहरणस्वरूप एक देश में राष्ट्रीय आय कुल आय का 50% भाग खेती में, 30% भाग उद्योगों में, 10% भाग सेवाओं तथा 10% भाग सबसे प्राप्त किया जाता है। इस स्थिति में विभिन्न क्षेत्रों को ध्यान में रखकर गोलाकार की कोणों का निर्माण निम्नलिखित अनुसार किया जाता है-

राष्ट्रीय आय में ………………………… |
कृषि में योगदान = \(\frac{50}{100}\) x 360° = 180°
उद्योगों में योगदान = \(\frac{30}{100}\) x 360° = 108°
सेवाओं में योगदान = \(\frac{10}{100}\) x 360 = 36°
शेष क्षेत्रों में योगदान = \(\frac{10}{100}\) x 360° = 36°

विभिन्न क्षेत्रों के योगदान को डिग्रियों में पता करके गोल आकार चित्र (Pie Diagram) का निर्माण किया जाता

4. चित्र लेख (Pictograph)-चित्र लेख वह विधि होती है, जिस द्वारा तस्वीरों को बनाकर आंकड़ों का प्रदर्शन करने का प्रयत्न किया जाता है। उदाहरणस्वरूप एक देश की जनसंख्या को 1951 तथा 1991 के समय का तुलनात्मक अध्ययन करना है तो इस स्थिति में देश X की जनसंख्या के आंकड़े इस प्रकार दिए गए हैं-
(Population of A Country) देश X की जनसंख्या
1951-4 करोड़
1991-7 करोड़

टिप्पणी = एक करोड़ इस प्रकार मनुष्यों, कारों अथवा उत्पादित वस्तुओं के चित्र बनाकर व्याख्या की जा सकती है।
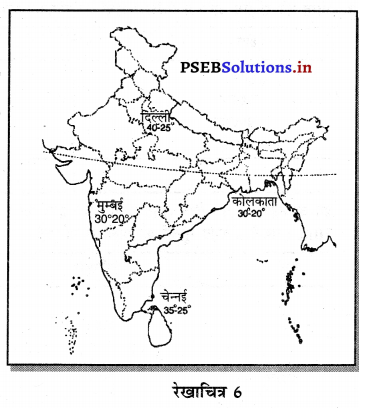
5. मानचित्र (Cartrograph)-मानचित्र की विधि में विभिन्न देश के नक्शों में उन देशों में प्राप्त होने वाली वस्तुएं सम्बन्धी आंकड़े प्रस्तुत किए जाते हैं। जब हमें तथ्यों को भौगोलिक आधार पर दिखाना हो तो मानचित्रों (Maps or Cartographes) का प्रयोग किया जाता है। उदाहरणस्वरूप भारत में प्रमुख नगरों दिल्ली, मुम्बई, कोलकाता तथा चेन्नई के अधिकतम तथा न्यूनतम तापमान का विवरण देना हो तो भारत के नक्शे में इन स्थानों के नाम लिखकर न्यूनतम तथा अधिकतम तापमान का विवरण दिया जा सकता है। इस विधि को मानचित्र विधि कहा जाता है।

मानचित्र अनुसार दिल्ली का अधिकतम तापमान 40° तथा न्यूनतम 25° है।
कोलकाता का अधिक तापमान 30° तथा न्यूनतम 20° है।
मुम्बई का अधिकतम तापमान 30° तथा न्यूनतम 20°
चेन्नई का अधिकतम तापमान 35° तथा न्यूनतम 25°