Punjab State Board PSEB 11th Class Maths Book Solutions Chapter 1 Sets Miscellaneous Exercise Questions and Answers.
PSEB Solutions for Class 11 Maths Chapter 1 Sets Miscellaneous Exercise
Question 1.
Decide, among the following sets, which sets are subsets of one and another:
A = {x : x ∈ R and x satisfy x2 – 8x + 12 = 0},
B = {2, 4, 6}, C = {2, 4, 6, 8…}, D = {6}.
Answer.
A={x : x ∈ R and x satisfies x2 – 8x + 12 = 0}
2 and 6 are the only solutions of x2 – 8x + 12 = 0.
∴ A = {2, 6}
B = {2, 4, 6}, C = {2, 4, 6, 8 …}, D = {6}
∴ D ⊂ A ⊂ B ⊂ C
Hence, A ⊂ B, A ⊂ C, B ⊂ C, D ⊂ A, D ⊂ B, D ⊂ C.
![]()
Question 2.
In each of the following, determine whether the statement is true or false. If it is true, prove it. If it is false, give an example.
(i) If x ∈ A and A ∈ B, then x ∈ B
(ii) If A⊂ B and B ∈ C, then A ∈ C
(iii) If A ⊂B and B ⊂ C, then A ⊂ C
(iv) If A ⊄ B and B ⊄ C, then A ⊄ C
(v) If x ∈ A and A ⊄ B, then x ∈ B
(vi) If A ⊂ B and x ∉ B, then x ∉ A
Answer.
(i) False
Let A = {1, 2} and B={1, {1, 2}, {3}}
2 ∈ {1, 2} and {1, 2} ∈ {{3}, 1, {1, 2}}
Now, A ∈ B
∴ However, 2 ∉ {{3}, 1, {1, 2}}
(ii) False
Let A = {2}, B = {0, 2}, and C = {1, {0, 2}, 3}
As A ⊂ B
B ∈ C
However, A ∉ C
(iii) True
Let A ⊂ B and B ⊂ C.
Let x ∈ A
x ∈ B [∵ A ⊂ B]
x ∈ C [∵ B ⊂ C]
∴ A ⊂ C
(iv) False
A = {1, 2}, B = {0, 6, 8}, and C = {0, 1, 2, 6, 9}
Accordingly, A ⊄ B and B ⊄ C.
However, A ⊂ C
(v) False
A = {3, 5, 7} and B = {3, 4, 6}
5 ∈ A and A ⊄ B
However, 5 ∉ B
(vi) True
Let A ⊂ B and x ∉ B.
To show x ∉ A
If possile, suppose x ∉ A
Then, x ∉ B, which is a conadicon as x ∉ B
∴ x ∉ A.
![]()
Question 3.
Let A, B and C be the sets such that A ∪ B = A ∪ C andA ∪ B = A ∪ C. Show that B = C.
Answer:
A ∪ B = A ∪ C
⇒ (A ∪ B) ∩ C = (A ∪ C) ∩ C
⇒ (A ∩ C) ∪ (B ∩ C) = C
⇒ (A ∩ B) ∪ (B ∩ C) = C …………….(i)
Again, A ∪ B = A ∪ C
⇒ (A ∪ B) ∩ B = (A ∪ C) ∩ B
⇒ B = (A ∩ B) ∪ (C ∩ B)
⇒ B = (A ∩ B) ∪ (B ∩ C)
From eqs. (i) and (ii), we get
B = C.
Question 4.
Show that the following four conditions are equivalent:
(i) A ⊂ B
(ii) A – B = Φ
(iii) A ∪ B = B
(iv) A ∩ B = A
Answer.
(i) ⟺
(ii) A ⊂ B ⟺ All elements of A are in B ⟺ A – B = Φ
(ii) ⟺
(iii) A – B = Φ ⟺ All elements of A are in B ⟺ A ∪ B = B.
(iii) ⟺ (iv)
A ∪ B = B ⟺ All the elements of A are in B.
⟺ All the elements of A are common in A and B ⟺ A ∩ B = A.
Thus, all the four given conditions are equivalent.
![]()
Question 5.
Show that if A ⊂ B, then C – B ⊂ C – A.
Answer.
Let A ⊂ B
To show: C – B ⊂ C – A
Let x ∈ C – B
⇒ x ∈ C and x ∉ B
⇒ x ∈ C and x ∉ A [A ⊂ B]
⇒ x ∈ C – A
C – B ⊂ C – A
Question 6.
Assume that P(A) = P(B). Show that A = B.
Answer.
Let P(A) =P (B)
To show: A = B
Let x ∈ A
A ∈ P(A) = P(B)
∴ x ∈ C,
for some C ∈ P(B)
C ⊂ B
∴ x ∈B
∴ A ⊂ B
Similarly, B ⊂ A
∴ A = B.
![]()
Question 7.
Is it true that for any sets A and B, P (A) ∪ P (B) = P (A ∪ B)? Justify your answer.
Answer.
Let A = {a}, B = {b} and A ∪ B = {a, b}
∴ P(A) = {Φ, {a}}, P(B) = {Φ, {b}}
P(A ∪ B) = {Φ, {a}, {b}, {a, b}} …………….(i)
and P(A) ∪ P(B) = {Φ, {a}, {b}} …………..(ii)
From eqs. (i) and (ii), we have
P(A ∪ B) ≠ P(A) ∪ P(B).
Question 8.
Show that for any sets A and B, A = (A ∩ B) ∪ (A – B) and A ∪ (B – A) = A ∪ B.
Answer.
(A ∩ B) ∪ (A – B) = (A ∩ B) ∪ (A ∩ B) [∵ A – B = A ∩ B]
= A ∩ (B ∪ B’) [Distributive law]
= A ∩ X, where X is universal set.
= A
A ∪ (B – A) = A ∪ (B ∩ A) [∵ B – A = B ∩ A’]
= (A ∪ B) ∩ (A ∪ A) [Distributive law]
= (A ∪ B) ∩ X
where X = A ∩ A’ is universal set
= A ∪ B [∵ A∪ B ⊂ X].
![]()
Question 9.
Using properties of sets, show that
(i) A ∪ (A ∩ B) = A
(ii) A ∩ (A ∪ B) = A.
Answer.
(i) A ∪ (A ∩B) = (A ∪ A) ∩ (A ∪ B) [Distributive law]
= A ∩ (A ∪ B) [∵ A ∪ A = A]
= A [∵ A ⊆ A ∪ B]
(ii) A ∩ (A ∪ B) = (A ∩ A) ∪ (A ∩ B)
= A ∪ (A ∩ B)
= A [∵ A ∩ B ⊂ A]
Question 10.
Show that A ∩ B=A ∩ C need not imply B = C.
Answer.
With the help of an example, we may try to establish it.
Let A = {1, 2}, B = {1, 3} and C = {1, 4}
Now A ∩ B = {1, 2} ∩{1, 3} = {1}
and A ∩ C = {1, 2} ∩{1, 4} = {1}
A ∩ B = A ∩ C
still B ≠ C.
![]()
Question 11.
Let A and B be sets. If A ∩ X = B ∩ X = Φ and A ∪ X = B ∪ X for some set X, show that A = B.
Answer. We have, A ∩ X = B ∩ X for some set X
⇒ A ∩ (A ∪ X) = A ∩(B ∪ X)
⇒ A = (A ∩ B) ∪ (A ∩ X) [∵ A ∩ (A ∪ X) = A]
⇒ A = (A ∩ B) ∪ Φ) [∵ A ∩ X = Φ (given)]
⇒ A = A ∩ B
⇒ A ⊂ B ………..(i)
Again, A ∪ X = B ∪ X
⇒ B ∩ (A ∪ X) = B ∩ (B ∪ X)
⇒ (B ∩ A) ∪ (B ∩ X) = B
⇒ (B ∩ A) ∪ Φ = B
⇒ B ∩ A = B
⇒ A ∩ B = B
⇒ B ⊂ A ……………(ii)
From eqs. (i) and (ii), we get A = B.
Question 12.
Find sets A, B and C such that A n B, B n C and A n C are non-empty sets and AnBnC=<(>.
Answer.
Let A = {1, 2}, B = {2, 3} and C = {1, 3}.
Clearly A ∩ B = {2}, B ∩ C = {3}and A ∩ C = {1}
i.e., A ∩ B, B ∩ C and A ∩ C are non-empty sets.
∴ (A ∩ B) ∩ C = {2} ∩ {1, 3}
⇒ A ∩ B ∩ C = Φ.
![]()
Question 13.
In a survey of 600 students in a school, 150 students were found to he taking tea and 225 taking coffee, 1Q0 were taking both tea and coffee. Find how many students were taking neither tea nor coffee?
Answer.
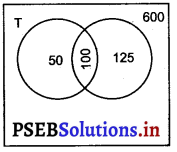
Here, n(T) = 150, n(C) = 225,
n(T ∩ C) = 100
Also we know that
n(T ∪ C) = n(T) + n(C) – n(T ∩ C)
= 150 + 225 – 100 = 275
Total mimber of students = 600
∴ Number of students who neither take tea nor coffee.
= 600 – n(T ∪ C)
= 600 – 275 = 325.
Question 14.
In a group pf students, 100 students know Hindi, 50 know English and 25 know bote. Each of the students knows either Hindi or English. How many students are there in tee group?
Answer.
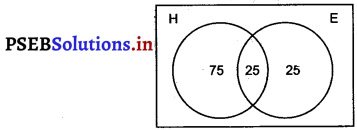
Here, n(H) = 100, n(E) = 50 and n(H ∩ E) = 25
We know that
n(H ∪ E) = n(H) + n(E) – n(H ∩ E)
= 100 + 50 – 25 = 125.
Hence there are 125 students in the group.
![]()
Question 15.
In a survey of 60 people, it was found that 25 people read newspaper H, 26 read newspaper T, 26 read newspaper 1,9 read bote H and 1,11 read both H and T, 8 read both T and 1, 3 read all three newspapers. Find:
(i) the number of people who read at least one of the newspapers.
(ii) the number of people who read exactly one newspaper.
Answer.
Let A be the set of people who read newspaper H.
Let B be the set of people who read newspaper T.
Let C be the set of people who read newspaper I.
Accordingly, n (A) = 25, n(B) = 26, and n(C) = 26
n(A ∩ C) = 9, n(A ∩ B) = 11, and n(B ∩ C) = 8 n(A ∩ B ∩ C) = 3
Let U be the set of people who took part in the survey.
(i) Accordingly,
n(A ∪ B ∪ C) = n(A) + n(B) + n(C) – n(A ∩ B) – n(B ∩ C) – n(C ∩ A)
+n(A ∩ B ∩ C)
= 25 + 26 + 26 – 11 – 8 – 9 + 3 = 52
Hence, 52 people read at least one of the newspapers.
(ii)
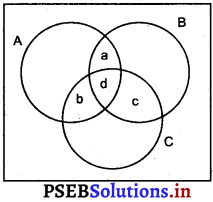
Let a be the number of people who read newspapers H and T only.
Let b denote the number of people who read newspapers I and H only.
Let c denote the number of people who read newspapers T and I only.
Let d denote the number of people who read all three newspapers.
Accordingly, d = n(A ∩ B ∩ C) = 3
Now, n(A ∩ B) = a + d,
n(B ∩ C) = c + d,
n(C ∩ A) = b + d
∴ a + d + c + d + b + d = 11 + 8 + 9 = 28
a + b + c + d = 28 – 2d
= 28 – 6 = 22
Hence, (52 – 22) = 30
people read exactly one newspaper.
Question 16.
In a survey it was found that 21 people liked product A, 26 liked product B and 29 liked product C. If 14 people liked products A and B, 12 people liked products C and A, 14 people liked products B and C and 8 liked all the three products. Find how many liked product C only?
Answer.
Let A, B, and C be the set of people who like product A, product B, and product C respectively.
Accordingly, n(A) = 21, n(B) = 26,
n(C) = 29, n(A ∩ B) = 14,
n(C ∩ A) = 12, n(B ∩ C) = 14,
n(A ∩ B ∩ C) = 8
The Venn diagram for the given problem can be drawn as
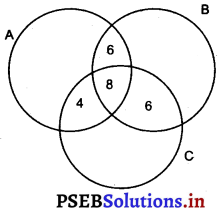
It can be seen that number of people who like product C only is
{29 – (4 + 8 + 6)} = 11.
