Punjab State Board PSEB 11th Class Maths Book Solutions Chapter 10 Straight Lines Ex 10.1 Textbook Exercise Questions and Answers.
PSEB Solutions for Class 11 Maths Chapter 10 Straight Lines Ex 10.1
Question 1.
Draw a quadrilateral in the Cartesian plane, whose vertices are (- 4, 5), (0, 7), (5, – 5) and (- 4, – 2). Also find its area.
Answer.
Let ABCD be the given quadrilateral with vertices A (- 4, 5), B (0, 7), C (5 – 5), and D (- 4. – 2).
Then, by plotting A, B, C and D on the Cartesian plane and joining AB, BC, CD and DA the given quadrilateral can be drawn as
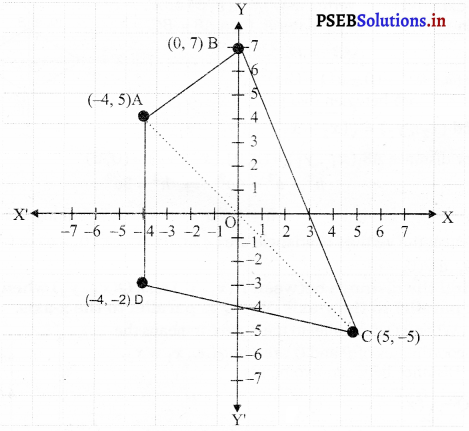
To find the area of quadrilateral ABCD, we draw one diagonal, say AC.
Accordingly, area (ABCD) = area (∆ABC) + area (∆ACD)
We know that the area of a triangle whose vertices are (x1, y1), (x2, y2) and (x3, y3) is \(\frac{1}{2}\) [x1 (y2 – y3) + x2 (y3 – y1) + x3 (y1 – y2)]
Therefore, area of ∆ABC
= \(\frac{1}{2}\) |- 4 (7 + 5) + 0(- 5 – 5) + 5 (5 – 7)| unit2
= \(\frac{1}{2}\) |- 4 (12) + 5 (- 2)| unit2
= \(\frac{1}{2}\) |- 48 – 10| unit2
= \(\frac{1}{2}\) |- 58| unit2
= \(\frac{1}{2}\) × 58 unit2
= 29 unit2
Area of MCD = \(\frac{1}{2}\) |- 4 (- 5 + 2) + 5(- 2 – 5) ± (- 4) (5 + 5)| unit2
= \(\frac{1}{2}\) |- 4 (- 3) + 5 (- 7) – 4(10)| unit2
= \(\frac{1}{2}\) |12 – 35 – 40| unit2
= \(\frac{1}{2}\) |- 63| unit2
= \(\frac{63}{2}\) unit2
Thus, area (ABCD) = (29 + \(\frac{63}{2}\)) unit2
= \(\frac{58+63}{2}\) unit2
= \(\frac{121}{2}\) unit2.
![]()
Question 2.
The base of an equilateral triangle with side 2a lies along the y-axis such that the mid point of the base is at the origin. Find vertices of the triangle.
Answer.
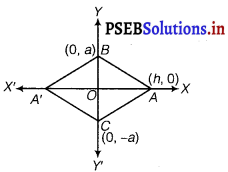
Let BC be the base of a triangle which lies on Y
Y-axis and third vertex may be A(h, 0) or A’.
Since, ∆ABC is an equilateral, then AB = BC.
∴ AB2 = BC2
⇒ (h – 0)2 + (0 – a2) = (2a)2
[∵ distance between two points (x1, y1) and (x2, y2)
= \(\left.\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\right]\)
For distance AB, (x1, y1) = (a, 0), (x2, y2) = (0, a)
h2 + a2 = 4a2
h2 = 3a2
h = ± √3 a [taking square root]
Hence, the vertices of triangle are (√3a, 0), (0, a), (0,- a) or (- √3, a) (0, a), (0, – a).
![]()
Question 3.
Find the distance between P(x1, y1) and Q(x2, y2) when:
(i) PQ is parallel to the y – axis
(ii) PQ is parallel to the x-aLg.
Answer.
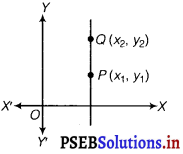
(i) When PQ is parallel to the Y-axis, it means the x-coordinates of P and Q are same i.e.,
x1 = x2.
∴ Distance between two points
PQ = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)
= \(\sqrt{\left(x_{1}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)
= \(\sqrt{\left(y_{2}-y_{1}\right)^{2}}=\left|y_{2}-y_{1}\right|\)
(ii) 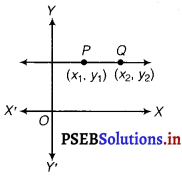
When PQ is parallel to X-axis, it means y-coordinates of P and Q are same i.e., y2 = y1
∴ Distance between two points PQ = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)
= \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{1}-y_{1}\right)^{2}}\) [∵ y2 = y1]
= \(\sqrt{\left(x_{2}-x_{1}\right)^{2}}\)
= |x2 – x1|
![]()
Question 4.
Find a point on the x-axis, which is equidistance from the points (7, 6) and (3, 4).
Answer.
Let any point P on the X-axis is (x, 0) as for a point on X-axis y-coordinate is zero and the given points are A (7, 6) and B (3, 4).
Given, PA = PB
⇒ PA2 = PB2
⇒ (x1 – x2)2 + (y1 – y2)2 = (x1 – x3)2 + (y1 – y3)2
where x1 = x, x2 = 7, y1 = 0, y2 = 6, x3 = 3, y3 = 4
(x – 7)2 + (0 – 6)2 = (x – 3)2 + (0 – 4)2
[∵ distance between two points = \(\left.\sqrt{\left(x_{1}-x_{2}\right)^{2}+\left(y_{1}-y_{2}\right)^{2}}\right]\)]
x2 + 49 – 14x + 36 = x2 + 9 – 6x + 16
⇒ – 14x + 6x = 25 – 36 – 49
⇒ – 8x = 25 – 85
⇒ Point P on X-axis = (\(\frac{15}{2}\), 0).
![]()
Question 5.
Find the slope of a line, which passes through the origin, and the mid-point of the line segment joining the points P(0, – 4) and B(8, 0).
Answer.
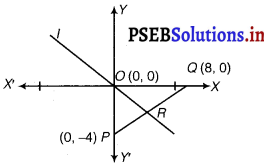
Given points are p (0, – 4) and Q (8, 0).
∴ x1 = 0, y1 = – 4, x2 = 8, y2 = 0
These points plotted in XY-plane are given below.
Mid-point of PQ is R = \(\left(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}\right)\)
= \(\left(\frac{0+8}{2}, \frac{-4+0}{2}\right)\) = (4, – 2)
∴ Slope of the OR = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
= \(\frac{-2-0}{4-0}=\frac{-2}{4}=-\frac{1}{2}\)
[∵ x = 0, x2 = 4, y1 = 0, y2 = – 2]
![]()
Question 6.
Without using the Pythagoras theorem show that the points (4, 4), (3, 5) and (- 1, – 1) are the vertices of a right angled triangle.
Answer.
In ∆ABC, we have
m1 = Slope of AB = \(\frac{4-5}{4-3}\) = – 1 and
m2 = Slope of AC = \(\frac{4-(-1)}{4-(-1)}\) = 1
Clearly, m1 m2 = – 1
This shows that AB is perpendicular to AC i. e.,
∠CAB = π/2
Hence, the given points are the vertices of a right-angled triangle.
Question 7.
Find the slope of the line, which makes an angle of 30° with the positive direction of y-axis measured anticlockwise.
Answer.
The line OP makes an angle of 30° with y-axis measured anticlockwise.
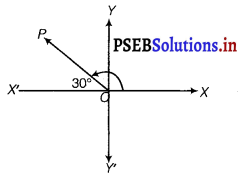
So OP makes an angle of 90° + 30° = 120° with positive direction of x-axis.
So, slope of OP = tan 120° = tan (180° – 60°) = – tan 60° = – √3.
![]()
Question 8.
Find the value of x for which the points (x, – 1), (2, 1) and (4, 5) are collinear.
Answer.
Given, points A (x, – 1), B (2, 1) and C (4, 5) are collinear.
Here, x1 = x, y1 = – 1, x2 = 2, y2 = 1, x3 = 4 and y3 = 5
∴ Slope of AB = Slope of BC
⇒ \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{y_{3}-y_{2}}{x_{3}-x_{2}}\)
⇒ \(\frac{1+1}{2-x}=\frac{5-1}{4-2}\)
⇒ \(\frac{2}{2-x}=\frac{4}{2}\)
⇒ 2 – x = 1
⇒ x = 2 – 1 = 1
![]()
Question 9.
Without using distance formula, show that points (- 2, – 1), (4, 0), (3, 3) and (- 3, 2) are vertices of a parallelogram.
Answer.
Let ABCD be a parallelogram, where vertices are
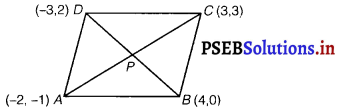
(x1, y1) → A (- 2, – 1),
(x2, y2) → B (4, 0),
(x3, y3) → C (3, 3) and
(x4, y4) → D (- 3, 2)
Mid-point of AC = \(\left(\frac{x_{1}+x_{3}}{2}, \frac{y_{1}+y_{3}}{2}\right)=\left(\frac{-2+3}{2}, \frac{-1+3}{2}\right)\)
= \(\left(\frac{1}{2}, \frac{2}{2}\right)=\left(\frac{1}{2}, 1\right)\)
[∵ mid-point of two points = \(\left(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}\right)\)]
Mid point of BD = \(\left(\frac{x_{2}+x_{4}}{2}, \frac{y_{2}+y_{4}}{2}\right)\)
= \(\left(\frac{4-3}{2}, \frac{0+2}{2}\right)=\left(\frac{1}{2}, 1\right)\)
∵ Mid-point of AC = Mid-point of BD
∴ ABCD is parallelogram.
Hence proved.
Question 10.
Find the angle between the xr-axis and the line joining the points (3, – 1) and (4, – 2).
Answer.
The slope of the line joining the points (3, – 1) and (4, – 2) is
m = \(\frac{-2-(-1)}{4-3}\)
= – 2 + 1 = – 1
Now, the inclination (θ) of the line joining the points (3, – 1) and (4, – 2) is given by tan θ = – 1
⇒ θ = (90° + 45°) = 135°
Thus, the angle between the x-axis and the line joining the points (3, – 1) and (4, – 2) is 135°.
![]()
Question 11.
The slope of a line is double of the slope of another line. If tangent of the angle between them is \(\frac{1}{3}\), find the slopes of the lines.
Answer.
Let m1 and m be the slopes of the two given lines such that m1 = 2m
We know that if 0 is the angle between the lines l1 and l2 with slopes m1 and m2 then
tan θ = \(\left|\frac{m_{2}-m_{1}}{1+m_{1} m_{2}}\right|\)
It is given that the tangent of the angle between the two lines is \(\frac{1}{3}\).
∴ \(\frac{1}{3}=\left|\frac{m-2 m}{1+(2 m) \cdot m}\right|\)
\(\frac{1}{3}=\frac{-m}{1+2 m^{2}}\) or
\(\frac{1}{3}=-\left(\frac{-m}{1+2 m^{2}}\right)=\frac{m}{1+2 m^{2}}\)Case I:
\(\frac{1}{3}=\frac{-m}{1+2 m^{2}}\)⇒ 1 + 2 m2 = – 3m
⇒ 2m + 3m + 1 = 0
⇒ 2m2 + 2m + m + 1 = 0
⇒ (m + 1) (2m + 1) = 0
⇒ m = – 1 or m = – \(\frac{1}{2}\)
If m = – 1, then the slopes of the lines are – 1 and – 2.
If m = – \(\frac{1}{2}\), then the slopes of the lines are – \(\frac{1}{2}\) and – 1.
Case II:
\(\frac{1}{3}=\frac{m}{1+2 m^{2}}\)
⇒ 2m2 + 1 = 3m
⇒ 2m2 – 2m – m + 1 = 0
⇒ (m – 1) (2m – 1) = 0
⇒ m = 1 or m = \(\frac{1}{2}\)
If m = 1, then the slopes of the lines are 1 and 2.
If m = \(\frac{1}{2}\), then the slopes of the lines are \(\frac{1}{2}\) and 1.
Hence, the slopes of the lines are – 1 and – 2 or – \(\frac{1}{2}\) and – 1 or 1 and 2 or \(\frac{1}{2}\) and 1.
![]()
Question 12.
A line passes through (x1, y1) and (h, k). If slope of the line is m, show that k – y1 = m (h – x1).
Answer.
The slope of the line passing through (x1, y1) and (h, k) is \(\frac{k-y_{1}}{h-x_{1}}\).
It is given that the slope of the line is
∴ \(\frac{k-y_{1}}{h-x_{1}}\) = m
⇒ k – y1 = m (h – x1)
Hence, k – y1 = m (h – x1).
Question 13.
If three points (h, 0), (a, b) and (0, k) lie on a line, show that \(\frac{a}{\boldsymbol{h}}+\frac{b}{\boldsymbol{k}}\) = 1.
Answer.
If the points A (h, 0), B (a, b) and C (0, k) lie on a line, then
Slope of AB = Slope of BC
\(\frac{b-0}{a-h}=\frac{k-b}{0-a}\)
⇒ \(\frac{b}{a-h}=\frac{k-b}{-a}\)
⇒ – ab = (k – b) (a – h)
⇒ – ab = ka – kh – ab + bh
⇒ ka + bh = kh
On dividing both sides by kh, we obtain
\(\frac{k a}{k h}+\frac{b h}{k h}=\frac{k h}{k h}\)
\(\frac{a}{h}+\frac{b}{k}\) = 1
Hence \(\frac{a}{h}+\frac{b}{k}\) = 1.
![]()
Question 14.
Consider the given population and year graph. Find the slope of the line AB and uaing it, find what will be the peculation in the year 2010?
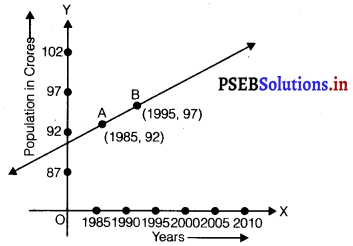
Answer.
Since line AB passes through points A(1985, 92) and B(1995, 97), its slope is = \(\frac{97-92}{1995-1985}=\frac{5}{10}=\frac{1}{2}\)
Let y be the population in the year 2010.
Then, according to the given graph, line AB must pass through point C (2010, y)
∴ Slope of AB = Slope of BC
⇒ \(\frac{1}{2}=\frac{y-97}{2010-1995}\)
⇒ \(\frac{1}{2}=\frac{y-97}{15}\)
⇒ \(\frac{15}{2}\) = y – 97
⇒ y – 97 = 7.5
⇒ y = 7.5 + 97 = 104.5
Thus, the slope of line AB is \(\frac{1}{2}\), while in the year 2010, the population will be 104.5 crores.
