PSEB 11th Class Maths Solutions Chapter 10 Straight Lines Ex 10.2

Punjab State Board PSEB 11th Class Maths Book Solutions Chapter 10 Straight Lines Ex 10.2 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 11 Maths Chapter 10 Straight Lines Ex 10.2

Question 1.
Write the equations for the x and y-axes.
Answer.
The y-coordinate of every point on the x-axis is 0.
Therefore, the equation of the x – axis is y = 0.
The x-coordinate of every point on the y – axis is 0.
Therefore, the equation of the y-axis is x = 0.

Question 2.
Find the equation of the line which passes through the point (- 4, 3) with slope \(\frac{1}{2}\).
Answer.
We know that the equation of the line passing through point (x₀, y₀), whose slope is m, is (y – y₀) = m (x – x₀).
Thus, the equation of the line passing through point (- 4, 3), whose slope is \(\frac{1}{2}\) is
(y – 3) = – (x + 4)
2 (y – 3) = x + 4
2y – 6 = x + 4
i.e., x – 2y + 10 = 0.

Question 3.
Find the equation of the line which passes through (0, 0) with slope m.
Answer.
We know that the equation of the line passing through point (x₀, y₀), whose slope is m, is
(y – y₀) = m (x – x₀)
Thus, the equation of the line passing through point (0, 0), whose slope is m is (y – 0) = m(x – 0)
i.e., y = mx.

Question 4.
Find the equation of the line which passes through (2, 2√3) and is inclined with the x-s’ at an angle of 75°.
Answer.
The slope of the line that inclines with the x-axis at an angle of 75° is m = tan75°
m = tan (45° + 30°)
= \(\frac{\tan 45^{\circ}+\tan 30^{\circ}}{1-\tan 45^{\circ} \tan 30^{\circ}}\)

= \(\frac{1+\frac{1}{\sqrt{3}}}{1-1 \cdot \frac{1}{\sqrt{3}}}\)

= \(\frac{\frac{\sqrt{3}+1}{\sqrt{3}}}{\frac{\sqrt{3}-1}{\sqrt{3}}}=\frac{\sqrt{3}+1}{\sqrt{3}-1}\)

We know that the equation of the line passing through point (x₀, y₀), whose slope is m, is (y – y₀) = m(x – x₀).
Thus, if a line passes though (2, 2√3) and inclines with the x-axis at an angle of 75°, then the equation of the line is given as
(y – 2√3) = (x – 2)
(y – 2√3) (√3 – 1) = (√3 + 1)(x – 2)
y(√3 – 1) – 2 √3 (√3 – 1) = x(√3 + 1) – 2 (√3 + 1)
(√3 + 1) x – (√3 – 1) y = 2√3 + 2 – 6 + 2√3
(√3 + 1) x – (√3 – 1) y = 4√3 – 4
i.e., (√3 + 1) x – (√3 – 1) y = 4(√3 – 1).

Question 5.
Find the equation of the line which intersects the x-axis at a distance of 3 units to the left of origin with slope – 2.
Answer.
It is known that if a line with slope m makes x-intercept d, then the equation of the line is given as y = m(x – d).
For the line intersecting the x-axis at a distance of 3 units to the left of the origin, d = – 3.
The slope of the line is given as m = – 2.
Thus, the required equation of the given line is
y = – 2 [x – (- 3)] = – 2x – 6
i.e., 2x + y + 6 = 0.

Question 6.
Find the equation of the line which intersects the y-axis at a distance of 2 units above the origin and makes an angle of 30° with the positive direction of the x-axis.
Answer.

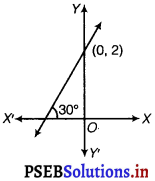
The line intersect the 7-axis at distance of 2 units above the origin. It show that the line passes through (0, 2).
It makes an angle 30° with the positive direction of X – axis.
1 X
So, the slope of the line is = tan 30° = \(\frac{1}{\sqrt{3}}\)
Thus, the equation of straight line is
y – y₁ = m (x – x₁)
y – 2 = \(\frac{1}{\sqrt{3}}\) (x – 0)
\(\frac{x}{\sqrt{3}}\) – y + 2 = 0
x – √3y + 2√3 = 0.

Question 7.
Find the equation of the line which passes through the points (- 1, 1) and (2, – 4).
Answer.
Given points are A (x₁, y₁) = (- 1, 1) and B(x₂, y₂) = (2, – 4), then equation of line AB is
y – y₁ = \(\frac{y-{2}-y-{1}}{x-{2}-x-{1}}\) (x – x₁)
⇒ y – 1 = \(\frac{-4-1}{2+1}\) (x + 1)
[x₁ = – 1, y₁ = 1, x₂ = 2, y₂ = – 4]
⇒ y – 1 = – \(\frac{5}{3}\) (x + 1)
⇒ 3y – 3 = – 5x – 5
⇒ 5x + 3y + 2 = 0

Question 8.
Find the equation of the line which is at a perpendicular distance of 5 units from the origin and the angle made by the perpendicular with the positive x – axis is 30°.
Answer.
If p is the length of the normal from the origin to a line and A is the angle made by the normal with the positive direction of the x-axis, then the equation of the line is given by x cos A + y sin A = p
Here, p = 5 units and A = 30°
Thus, the required equation of the given line is x cos 30° + y sin 30° = 5
x \(\frac{\sqrt{3}}{2}\) + y . \(\frac{1}{2}\) = 5
i.e., √3x + y = 10.

Question 9.
The vertices of ∆PQR are P(2, 1), Q(- 2, 3) and R(4, 5). Find equation of the median through the vertex R.
Answer.
Since, median bisects the opposite sides i. e., S is the mid-point of PQ.
S = \(\left(\frac{\ddot{x}-{1}+x-{2}}{2}, \frac{y-{1}+y-{2}}{2}\right)\)

= \(\left(\frac{2-2}{2}, \frac{1+3}{2}\right)=\left(0, \frac{4}{2}\right)\)

= (0, 2)

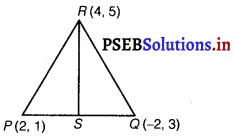
y – y₁ = \(\frac{y-{2}-y-{1}}{x-{2}-x-{1}}\) (x – x₁)
⇒ y – 5 = \(\frac{2-5}{0-4}\) (x – 4)
[∵ x₁ = 2, y₁ = 1, x₁ = – 2, y₁ = 3]
⇒ y – 5 = \(\frac{-3}{-4}\) (x – 4)
4y – 20 = 3x – 12
⇒ 3x – 4y + 8 = 0

Question 10.
Find the equation of the line passing through (- 3, 5) and perpendicular to the line through the points (2, 5) and (- 3, 6).
Answer.
The slope of the line joining the points (2, 5) and (- 3, 6) is
m = \(\frac{6-5}{-3-2}=\frac{1}{-5}\)

We know that two non-vertical lines are perpendicular to each other if and only if their slopes are negative reciprocals of each other.

Therefore, slope of the line perpendicular to the line through the points (2, 5) and (- 3, 6)
= \(-\frac{1}{m}=-\frac{1}{\left(\frac{-1}{5}\right)}\) = 5

Now, the equation of the line passing through point (- 3, 5), whose slope is 5, is
(y – 5) = 5 (x + 3)
y – 5 = 5x + 15
i.e., 5x – y + 20 = 0.

Question 11.
A line perpendicular to the line segment joining the points (1, 0) and (2, 3) divides it in the ratio 1 : n. Find the equation of the line.
Answer.

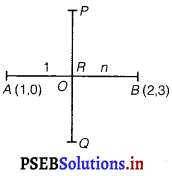
Let the given points are A(1, 0) and B(2, 3).
Let the line PQ divide AB in the ratio 1 : n at R internally.
Then, coordinates of R = \(\left(\frac{1 \times x-{2}+n \times x-{1}}{1+n}, \frac{1 \times y-{2}+n \times y-{1}}{1+n}\right)\)

= \(\left(\frac{1 \times 2+n \times 1}{1+n}, \frac{1 \times 3+n \times 0}{1+n}\right)\)

[∵ x₁ = 1, y₁ = 0, x₂ = 2, y₂ = 3]

= \(\left(\frac{n+2}{n+1}, \frac{3}{1+n}\right)\)

Let the slope of the line is m.
Also, PQ ⊥ AB
∴ Slope of the line PQ × Slope of the line AB = – 1
⇒ m × \(\frac{y-{2}-y-{1}}{x-{2}-x-{1}}\) = – 1

⇒ m × \(\frac{3-0}{2-1}\) = – 1

[∵ x₁ = 1, y₁ = 0, x₂ = 2, y₂ = 2]

⇒ m × 3 = – 1
⇒ m = – \(\frac{1}{3}\)

Now, equation of line PQ y using y – y₀ = m (x – x₀)

y – \(\frac{3}{1+n}\) = \(\frac{-1}{3}\left(x-\frac{n+2}{n+1}\right)\)

[∵ R\(\left(\frac{n+2}{n+1}, \frac{3}{1+n}\right)\) = (x₁, y₁)

\(\frac{3(n+1) y-9}{1+n}=\frac{-x(n+1)+(n+2)}{n+1}\)

⇒ 3 (n + 1) y – 9 = – x (n + 1) + (n + 2)
⇒ x (n + 1) + 3 (n + 1) y = n + 2 + 9
⇒ x (n + 1) + 3 (n + 1) y = n + 11
Which is the required equation of line.

Question 12.
Find the equation of a line that cuts off equal intercepts on the coordinate axes and passes through the point (2, 3).
Answer.
The equation of a line in the intercept form is
\(\frac{x}{a}+\frac{y}{b}\) = 1 …………….(i)
Here, a and b are the intercepts on x and y axes respectively.
It is given that the line cuts off equal intercepts on both the axes.
This means that a = b.
Accordingly, equation (i) reduces to
\(\frac{x}{a}+\frac{y}{a}\) = 1
x + y = a ………………(ii)
Since the given line passes through point (2, 3), equation (ii) reduces to
2 + 3 = a
a = 5
On substituting the value of a in equation (ii), we obtain x + y = 5, which is the required equation of the line.

Question 13.
Find equation of the line passing through the point (2, 2) and cutting off intercepts on the axes whose sum is 9.
Answer.
The equation of a line in the intercept form is
\(\frac{x}{a}+\frac{y}{b}\) = 1 ……………(i)
Here, a and b are the intercepts on x and y axes respectively.
It is given that a + b = 9
⇒ b = 9 – a ………….. (ii)
From equations (i) and (ii), we obtain
\(\frac{x}{a}+\frac{y}{9-a}\) = 1 ………..(iii)

It is given that the line passes through point (2, 2).
Therefore, equation (iii) reduces to \(\frac{2}{a}+\frac{2}{9-a}\) = 1
⇒ \(2\left(\frac{1}{a}+\frac{1}{9-a}\right)\) = 1

⇒ \(2\left(\frac{9-a+a}{a(9-a)}\right)\) = 1

⇒ \(\frac{18}{9 a-a^{2}}\) = 1

⇒ 18 = 9a – a²
⇒ a² – 9a + 18 = 0
⇒ a² – 6a – 3a + 18 = 0
⇒ a (a – 6) – 3 (a – 6) = 0
⇒ (a – 6) (a – 3) = 0
⇒ a = 6 or a = 3
If a = 6 and b = 9 – 6 =3, then the equation of the line is \(\frac{x}{6}+\frac{y}{3}\) = 1
⇒ x + 2y – 6 = 0
If a = 3 and = 9 – 3 = 6, then the equation of the line is
\(\frac{x}{6}+\frac{y}{3}\) = 1
⇒ 2x + y – 6 = 0.

Question 14.
Find equation of the line through the point (0, 2) making an angle – with the positive x-axis. Also, find the equation of line 3 parallel to it and crossing the y-axis at a distance of 2 units below the origin.
Answer.

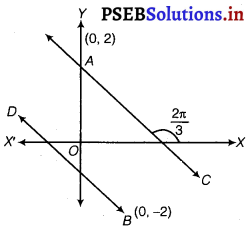
Slope of the line = tan \(\frac{2 \pi}{3}\)
tan (π – \(\frac{\pi}{3}\)) = tan \(\frac{\pi}{3}\) = – √3
Equation of the line AC with slope = – √3 and passing through the point D given by
y – 2 = – √3(x – 0)
⇒ √3x + y – 2 = 0
For beyond past, we take another line BD parallel to AC.
∴ Slope of the line BD = Slope of AC = – √3
BD is passing through the point D{0, – 2)
∴ Equation of BD is y + 2 = √3(x – 0)
⇒ √3x + y + 2 = 0
Hence, equation of AC and BD are,
√3x + y – 2 = 0 and √3x + y + 2 = 0.

Question 15.
The perpendicular from the origin to a line meets it at the point (- 2, 9), find the equation of the line.
Answer.
The slope of the line joining the origin (0, 0) and point (- 2, 9) is
m₁ = \(\frac{9-0}{-2-0}=-\frac{9}{2}\)

Accordingly, the slope of the line, perpendicular to the line joining the origin and point (- 2, 9) is
m₂ = \(-\frac{1}{m-{1}}=-\frac{1}{\left(-\frac{9}{2}\right)}=\frac{2}{9}\)

Now, the equation of the line passing through point (- 2, 9) and having a slope m2 is
(y – 9) = \(\frac{2}{9}\) (x + 2)
9y – 81 = 2x + 4
2x – 9y + 85 = 0.

Question 16.
The length L (in centimetre) of a copper rod is a linear function of its Celsius temperature C. In an experiment, if L = 124.942 when C = 20 and L = 125.134 when C = 110, express L in terms of C.
Answer.
Since, L is linear function of C.
L = a + bC …………….(i)
For L = 124.942, C = 20
124.942 = a + 20b ………………(ii)
For L = 125.134 C = 110
∴ 125.134 = a + 1106 ……………(iii)
Subtracting eq. (ii) from eq. (iii), we get
0. 192 = 90b
b = \(\frac{0.192}{90}\) = 0.00213
From eq. (ii),
124.942 = a + 20 × 0.00213 = a + 0.0426
a = 124.942 – 0.0426 = 124.8994
Hence from eq. (i) L in terms of C is
L = 124.8994 + 0.00213C.

Question 17.
The owner of a milk store finds that, he can sell 980 litres of milk each week at Rs. 14/litre and 1220 litres of milk each week at Rs. 16/litre. Assuming a linear relationship between selling price and demand, how many litres could he sell weekly at Rs. 17/litre?
Answer.
Let price and litre be denoted in ordered pair (x, y), where x denotes the ₹ per litre and y denotes the quantity of milk in litre.
Given, (14980) and (161220) are two points.
Let linear relations i. e., linear equation be
y – y₁ = \(\frac{y-{2}-y-{1}}{x-{2}-x-{1}}\) (x – x₁)

y – 980 = \(\frac{1220-980}{16-14}\) (x – 14)

y – 980 = \(\frac{240}{2}\) (x – 14)
[∵ x₁ = 14, y₁ = 980, x₂ = 16, y₂ = 1220]
⇒ y – 980 = 120 (x – 14)
⇒ y – 980 = 120x – 120 × 14
⇒ 120x – y = 1680 – 980
⇒ 120x – y = 700
When price JC = 17,
120 x 17 – y = 700
y = 2040 – 700 = 1340
He will sell weekly 1340 L milk at the rate of ₹ 172.

Question 18.
P(a, b) is the mid-point of a line segment between axes. Show that equation of the line is \(\frac{x}{a}+\frac{y}{b}\) = 2.
Answer.
Let AB be the line segment between the axes and let P(a, b) be its mid-point.

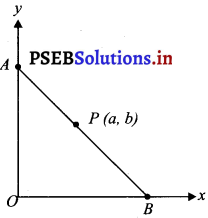
Let the coordinates of A and B be (0, y) and (x, 0) respectively.
Since P(a, b) is the mid-point of AB.
\(\left(\frac{0+x}{2}, \frac{y+0}{2}\right)\) = (a, b)

\(\left(\frac{x}{2}, \frac{y}{2}\right)\) = (a, b) and

\(\frac{x}{2}\) = a and \(\frac{y}{2}\) = b
x = 2a and y = 2b
Thus, the respectively coordinares of A and B are (0, 2b) and (2a, 0).
The equation of the line passing through points (0, 2b) and (2a, 0) is

(y – 2b) = \(=\frac{(0-2 b)}{(2 a-0)}\) (x – 0)

y – 2b = \(\frac{-2 b}{2 a}\) (x)

a (y – 2b) = – bx
ay – 2ab = – bx
i.e., bx + ay = 2ab
On dividing both sides by ab, we obtain
\(\frac{b x}{a b}+\frac{a y}{a b}=\frac{2 a b}{a b}\)

⇒ \(\frac{x}{a}+\frac{y}{b}\) = 2
Thus, the equation of the line is \(\frac{x}{a}+\frac{y}{b}\) = 2.

Question 19.
Point R (h, k) divides a line segment between the axes in the ratio 1 : 2. Find equation of the line.
Answer.

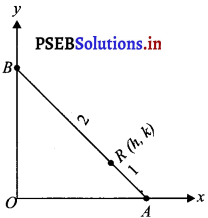
Let AB be the line segment between the axes such that point R(h, k) divides AB in the ratio 1 : 2.
Let the respective coordinates of A and B be (x, 0) and (0, y).
Since point R(h, k) divides AB in the ratio 1 : 2, according to the section formula,
(h, k) = \(=\left(\frac{1 \times 0+2 \times x}{1+2}, \frac{1 \times y+2 \times 0}{1+2}\right)\)

(h, k) = \(\left(\frac{2 x}{3}, \frac{y}{3}\right)\)

⇒ h = \(\frac{2 x}{3}\) and k = \(\frac{y}{3}\)
⇒ x = \(\frac{3 h}{2}\) and y = 3k

Therefore, the respective coordinates of A and B are (\(\frac{3 h}{2}\), o) and (0, 3k).

Now, the equation of line AB passing through points (\(\frac{3 h}{2}\), 0) and (0, 3k) is

(y – 0) = \(\frac{3 k-0}{0-\frac{3 h}{2}}\) (x – \(\frac{3 h}{2}\))

y = – \(\frac{2 k}{h}\) (x – \(\frac{3 h}{2}\))
hy = – 2kx + 3hk
i.e., 2kx + hy = 3hk
Thus, the required equation of the line is 2kx + hy = 3hk.

Question 20.
By using the concept of equation of a line, prove that the three points (3, 0), (- 2, – 2) and (8, 2) are collinear.
Answer.
In order to show that points (3, 0) (- 2, – 2) and (8, 2) are coimear, it suffices to show that the line passing through points (3, 0) and (- 2, – 2) also passes through point (8, 2).
The equation of the line passing through points (3, 0) and (- 2, – 2) is
(y – 0) = \(\frac{(-2-0)}{(-2-3)}\) (x – 3)

y = \(\frac{-2}{-5}\) (x – 3)
5y = 2x – 6
i.e., 2x – 5y = 6
It is observed that at x = 8 and y = 2,
5y = 2x – 6
i.e., 2x – 5y = 6
It is observed that at x = 8 and y = 2,
L.H.S. = 2 × 8 – 5 × 2
= 16 – 10 = 6 = R.H.S.
Therefore, the line passing through points (3, 0) and (- 2, – 2) also passes through point (8, 2).
Hence, points (3, 0), (- 2, – 2) and (8, 2) are collinear.