PSEB 11th Class Maths Solutions Chapter 11 Conic Sections Ex 11.2

Punjab State Board PSEB 11th Class Maths Book Solutions Chapter 11 Conic Sections Ex 11.2 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 11 Maths Chapter 11 Conic Sections Ex 11.2

Question 1.
Find the coordinates of the focus, axis of the parabola, the equation of the directrix and the length .of the latus rectum for y² = 12x.
Answer.
The given equation is y² = 12x.
Here, the coefficient of x is positive.
Hence, the parabola opens towards the right.
On comparing this equation with y² = 4 ax, we obtain
4a = 12
⇒ a = 3.
∴ Coordinates of the focus = (a, 0) = (3, 0)
Since the given equation involves y², the axis of the parabola is the x-axis.
Equation of directrix, x = – a i.e., x = – 3 i.e., x + 3 = 0
Length of latus rectum = 4a = 4 × 3 = 12.

Question 2.
Find the coordinates of the focus, axis of the parabola, the equation of the directrix and the length of the latus rectum for x² = 6y.
Answer.
The given equation is x² = 6y.
Here, the coefficient of y is positive. Hence, the parabola opens upwards.
On comparing this equation with x² = 4ay , we obtain
4a = 6
⇒ a = \(\frac{3}{2}\).
Coordinates of the focus = (0, a) = (0, \(\frac{3}{2}\))
Since the given equation involves x , the axis of the parabola is the y-axis.
Equation of directrix, y = – a i.e., y = – \(\frac{3}{2}\)
Length of latus rectum = 4a = 6.

Question 3.
Find the coordinates of the focus, axis of the parabola, the equation of the directrix and the length of the latus rectum for y² = – 8x.
Answer.
Here, the coefficient of x is negative.
Hence, the parabola opens towards the left.
On comparing this equation with y² = – 4 ax , we obtain
– 4a = – 8
⇒ a = 2
Coordinates of the focus = (- a, 0) = (- 2, 0)
Since the given equation involves y², the axis of the parabola is the x-axis.
Equation of directrix, x = a i.e., x = 2
∴ Length of latus rectum = 4a = 8.

Question 4.
Find the coordinates of the focus, axis of the parabola, the equation of the directrix and the length of the latus rectum for x² = – 16y.
Ans.
The given equation is x² = – 16y
Here, the coefficient of y is negative.
Hence, the parabola opens downwards.
On comparing this equation with x² = – 4ay, we obtain
– 4a = – 16
⇒ a = 4
∴ Coordinates of the focus = (0, – a) = (0, – 4)
Since the given equation involves x², the axis of the parabola is the y-axis.
Equation cf directrix, y = a i.e., y = 4
Length of latus rectum = 4a = 16.

Question 5.
Find the coordinntes of the focus, axis of the parabola, the equation of the directrix and the length of the latus rectum for y² = 10x.
Answer.
The given equation is y² = 10x.
Here, the coefficient of x is positive.
Hence, the parabola opens towards the right.
On comparing this equation with y² = 4ax, we obtain
4a = 10
⇒ a = \(\frac{5}{2}\)
Coordinates of the focus = (a, 0) = (\(\frac{5}{2}\), 0)
Since the given equation involves y², the axis of the parabola is the x-axis.
Equation of directrix, x = – a, i.e., x = – \(\frac{5}{2}\)
Length of latus rectum = 4a = 10.

Question 6.
Find the coordinates of the focus, axis of the parabola, the equation of the directrix and the length of the latus rectum for x\(\frac{5}{2}\) = – 9y.
Answer.
We have, equation of parabola is x² = – 9y
So, axis of symmetry is along x-axis.
The coefficient of y is negative, so parabola opens downward.
On comparing with the equation,
x² = – 4ay, we get a = \(\frac{9}{4}\)
Thus, the focus is (0, – a) i.e., (0, – \(\frac{9}{4}\))
Equation of directrix is y = a i.e., y = 9/4.
Length of latus rectum = 4a i.e., 9.

Question 7.
Find the equation of the parabola that satisfies the given conditions : Focus (6, 0): directrix x = – 6.
Answer.
Given, focus (6, 0) and directrix, x = – 6.
Here, we see that in focus, x-coordinate is positive and y-coordinate is zero.
So, focus lies on the positive direction of X-axis i.e., equation of parabola will be of the form y² = 4ax with a = 6.
Hence, required equation is
y² = 4 × 6x
⇒ y² = 24x

Question 8.
Find the equation of the parabola that satisfies the given conditions : Focus (0, – 3); directrix y = 3.
Answer.
Given, focus = (0, – 3); directrix y=3.
Since the focus lies on the y-axis, the y-axis is the axis of the parabola.
Therefore, the equation of the parabola is either of the form x² = 4 ay or x² = – 4ay.
It is also seen that the directrix, y = 3 is above the x-axis, while the focus (0, – 3) is below the x-axis.
Hence, the parabola is of the form x²= – 4ay.
Here, a = 3.
Thus, the equation of the parabola is x² = – 12y.

Question 9.
Find the equation of the parabola that satisfies the given conditions : Vertex (0, 0); focus (3, 0).
Answer.
Given, vertex (0, 0); focus (3, 0).
Since the vertex of the parabola is (0, 0) and the focus lies on the positive x-axis, x-axis is the axis of the parabola, while the equation of the parabola is of the form y² = 4ax.
Since the focus is (3, 0), a = 3.
Thus, the equation of the parabola is y² = 4 × 3 × x, i.e., y² = 12x.

Question 10.
Find the equation of the parabola that satisfies the given conditions: Vertex (0, 0) focus (-2, 0).
Answer.
Given, vertex (0, 0); focus (- 2, 0)
Since the vertex of the parabola is (0, 0) and the focus lies on the negative x-axis, x-axis is the axis of the parabola, while the equation of the parabola is of the form y² = – 4ax.
Since the focus is (- 2, 0), a = 2.
Thus, the equation of the parabola is y² = – 4(2)x, i.e., y = – 8x.

Question 11.
Find the equation of the parabola that satisfies the given conditions: Vertex (0, 0) passing through (2, 3) and axis is along x-axis.
Answer.
Since the vertex is (0, 0) and the axis of the parabola is the x-axis, the equation of the parabola is either of the form
y² = 4ax or y² = – 4ax.
The parabola passes through point (2, 3), which lies in the first quadrant.
Therefore, the equation of the parabola is of the form y² = 4 ax, while point (2, 3) must satisfy the equation y² = 4ax.
3² = 4a(2)
a = \(\frac{9}{8}\)
Thus, the equation of the paraola is y² = – 4(2)x, i.e., y² = – 8x.

Question 12.
Find the equation of the parabola that statisfies the given conditions; Vertex (0, 0), passing through (5, 2) and symmetric with respect to y-axis.
Answer.

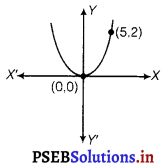
Since, the parabola is symmetric about Y-axis and has its vertex at the origin, so the equation is of the form x² = 4ay or x² = – 4ay.
But parabola passes through (5, 2) which lies in the first quadrant. It must open upward.
Thus, the equation is of the form
x² = 4ay ……………….(i)
Since, parabola passes through (5, 2)
(5)² = 4a(2)
⇒ 25 = 8a
⇒ a = \(\frac{25}{8}\)
On putting the value of a in eq.(i), we get
x² = 4 (\(\frac{25}{8}\)) y
⇒ x² = \(\frac{25}{8}\) y