PSEB 11th Class Maths Solutions Chapter 11 Conic Sections Ex 11.4

Punjab State Board PSEB 11th Class Maths Book Solutions Chapter 11 Conic Sections Ex 11.4 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 11 Maths Chapter 11 Conic Sections Ex 11.4

Question 1.
Find the coordinates of the foci and the vertices, the eccentricity, and the length of the latus rectum of the hyperbola
\(\frac{x^{2}}{16}-\frac{y^{2}}{9}\) = 1.
Answer.
The given equation is \(\frac{x^{2}}{16}-\frac{y^{2}}{9}\) = 1 or \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) = 1.

On comparing this equation with the standard equation of hyperbola i.e., \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) = 1, we obtain a = 4 and b = 3.

We know that
a² + b² = c²
4² + 3² = 25
⇒ c = 5
Therefore, The coordinates of the foci are (± 5, 0).
The coordinates of the vertices are (± 4, 0).
Eccentricity e = \(\frac{c}{a}=\frac{5}{4}\)

Length of latusrectum = \(\frac{2 b^{2}}{a}=\frac{2 \times 9}{4}=\frac{9}{2}\).

Question 2.
Find the coordinates of the foci and the vertices, the eccentricity, and the length of the latus rectum of the hyperbola
\(\frac{y^{2}}{9}-\frac{x^{2}}{27}\) = 1.
Answer.
The given equation is \(\frac{y^{2}}{9}-\frac{x^{2}}{27}\) = 1 or \(\frac{y^{2}}{3^{2}}-\frac{x^{2}}{(\sqrt{27})^{2}}\) = 1.
On comparing this equation with the standard equation of hyperbola i.e., \(\frac{y^{2}}{a^{2}}-\frac{x^{2}}{b^{2}}\) = 1, we obtain a = 3 and b = √27.

We know that a² + b² = c²
c² = 3² + (√27)²
= 9 + 27 = 36
⇒ c = 6
Therefore, the coordinates of the foci are (0, ± 6).
The coordinates of the vertices are (0, ± 3).
Eccentricity, e = \(\frac{c}{a}=\frac{6}{3}\) = 2.
Length of latusrectum = \(\frac{2 b^{2}}{a}=\frac{2 \times 27}{3}\) = 18.

Question 3.
Find the coordinates of the foci and the vertices, the eccentricity, and the length of the latus rectum of the hyperbola
9y² – 4x² = 36.
Answer.
The given equation is 9y² – 4x² = 36
It can be written as 9y² – 4x² = 36
or \(\frac{y^{2}}{4}-\frac{x^{2}}{9}\) = 1

or \(\frac{y^{2}}{2^{2}}-\frac{x^{2}}{3^{2}}\) = 1 ………….(i)
On comparing equation (i) with the standard equation of hyperbola i.e., \(\frac{y^{2}}{a^{2}}-\frac{x^{2}}{b^{2}}\) = 1, we obtain a = 2 and b = 3.

We know that a² + b² = c²
c² = 4 + 9 = 13
⇒ c = √13.
Therefore, the coordinates of the foci are (0, ± √13).
The coordinates of the vertices are (0, ± 2).
Eccentricity, e = \(\frac{c}{a}=\frac{\sqrt{13}}{2}\)

Length of latus rectum = \(\frac{2 b^{2}}{a}=\frac{2 \times 9}{2}\) = 9.

Question 4.
Find the coordinates of the foci and the vertices, the eccentricity, and the length of the latus rectum of the hyperbola 16x² – 9y² = 576.
Answer.
The given equation is 16x² – 9y² = 576
It can be written as 16x² – 9y² = 576

⇒ \(\frac{x^{2}}{36}-\frac{y^{2}}{64}\) = 1

⇒ \(\frac{x^{2}}{6^{2}}-\frac{y^{2}}{8^{2}}\) = 1 ………………(i)

On comparing equation (i) with the standard equation of hyperbola i.e.,
\(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) = 1, we obtain a = 6 and b = 8.
We know that a² + b² = c²
c² = 36 + 64 = 100
⇒ c = 10
Therefore, the coordinates of the foci are (± 10, 0).
The coordinates of the vertices are (± 6, 0).
Eccentricity, e = \(\frac{c}{a}=\frac{10}{6}=\frac{5}{3}\).

Length of larus rectum = \(\frac{2 b^{2}}{a}=\frac{2 \times 64}{6}=\frac{64}{3}\).

Question 5.
Find the coordinates of the foci and the vertices, the eccentricity, and the length of the latus rectum of the hyperbola 5y² – 9x² = 36.
Answer.
The given equation is 5y² – 9x² = 36.
⇒ \(\frac{y^{2}}{\left(\frac{36}{5}\right)}-\frac{x^{2}}{4}\) = 1

⇒ \(\frac{y^{2}}{\left(\frac{6}{\sqrt{5}}\right)^{2}}-\frac{x^{2}}{2^{2}}\) = 1
On comparing equation (i) with the standard equation of hyperbola i.e., \(\frac{y^{2}}{a^{2}}-\frac{x^{2}}{b^{2}}\) = 1,

we obtain a = \(\frac{6}{\sqrt{5}}\) = and b = 2.

We know that a² + b² = c².
∴ c² = \(\frac{36}{5}+4=\frac{56}{5}\)

⇒ c = \(\sqrt{\frac{56}{5}}=\frac{2 \sqrt{14}}{\sqrt{5}}\)

Therefore, the coordinates of the foci are (0, ± \(\frac{2 \sqrt{14}}{\sqrt{5}}\))

The coordinates of the vertices are (o, ± \(\frac{6}{\sqrt{5}}\)).

Eccentricity, e = \(\frac{c}{a}=\frac{\left(\frac{2 \sqrt{14}}{\sqrt{5}}\right)}{\left(\frac{6}{\sqrt{5}}\right)}=\frac{\sqrt{14}}{3}\)

Length of latus rectum = \(\frac{2 b^{2}}{a}=\frac{2 \times 4}{\left(\frac{6}{\sqrt{5}}\right)}=\frac{4 \sqrt{5}}{3}\)

Question 6.
Find the coordinates of the foci, and the vertices, the eccentricity, and the length of the latus rectum of the hyperbola
49y² – 16x² = 784.
Answer.
The given equation is 49y² – 16x² = 784
it can be writtern as 49y² – 16x² = 784

or \(\frac{y^{2}}{16}-\frac{x^{2}}{49}\) = 1

or \(\frac{y^{2}}{4^{2}}-\frac{x^{2}}{7^{2}}\) = 1 ……………….(i)

On comparing equation (i) with the standard equation of hyperbola i.e., \(\frac{y^{2}}{a^{2}}-\frac{x^{2}}{b^{2}}\) = 1,
we obtain a = 4 and b = 7.

We knowthat, a² + b² = c².
∴ c² = 16 + 49 = 65
⇒ c = √65
Therefore, The coordinates of the foci are (0, ± √65
The coordinates of the vertices are (0, ± 4).

Eccentricity, e = \(\frac{c}{a}=\frac{\sqrt{65}}{4}\).

Length of lattis rectum = \(\frac{2 b^{2}}{a}=\frac{2 \times 49}{4}=\frac{49}{2}\).

Question 7.
Find the equation of the hyperbola satisfying the given conditions : Vertices (± 2, 0), foci (± 3, 0).
Answer.
Given, vertices (± 2, 0), foci (± 3, 0)
Here, the vertices are on the x-axis.
Therefore, the equation of the hyperbola is of the form \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) = 1.
Since the vertices are (± 2, 0), a = 2
Since the foci are (± 3, 0), c = 3
We know that a² + b² = c².
∴ 2² + b² = 3²
b² = 9 – 4 = 5
Thus, the equation of the hyperbola is \(\frac{x^{2}}{4}-\frac{y^{2}}{5}\)= 1.

Question 8.
Find the equation of the hyperbola satisfying the given conditions : Vertices (0, ± 5), foci (0, ± 8).
Ans.
We have,vertices (0, ± a) = (0, ± 5) = a = 5
and foci(0, ± c) = (0, ± 8)
⇒ c = 8
We know that, c² = a² + b²
⇒ 64 = 25 + b²
⇒ b² = 64 – 25
⇒ b² = 39
Here, the foci and vertices lie on Y-axis, therefore the equation of hyperbola is of the form \(\frac{y^{2}}{a^{2}}-\frac{x^{2}}{b^{2}}\) = 1
i.e. \(\frac{y^{2}}{25}-\frac{x^{2}}{39}\) = 1

Question 9.
Find the equation of the hyperbola satisfying the given conditions : Vertices (0, ± 3), foci (0, ± 5).
Answer.
Given, vertices (0, ± 3), foci (0, ± 5)
Here, the vertices are on the y-axis.
Therefore, the equation of the hyperbola is of the form \(\frac{y^{2}}{a^{2}}-\frac{x^{2}}{b^{2}}\) = 1.
Since the vertices are (0, ± 3), a = 3.
Since the foci are (0, ± 5), c = 5.
We know that a² + b² = c².
3² + b² = 5²
⇒ b² = 25 – 9 = 16.
Thus, the equation of the hyperbola is \(\frac{y^{2}}{9}-\frac{x^{2}}{16}\) = 1.

Question 10.
Find the equation of the hyperbola satisfying the given conditions : Foci (± 5, 0), the transverse axis is of length 8.
Answer.
Given, foci (± 5, 0), the transverse axis is of length 8.
Here, the foci are on the x-axis.
Therefore, the equation of the hyperbola is of the \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) = 1.
Since the foci are (± 5, 0), c = 5.
Since the length of the transverse axis is 8, 2a = 8
⇒ a = 4.
We know that, a² + b² = c².
∴ 4² + b² = 5²
⇒ b² = 25 – 16 = 9

Question 11.
Find the equation of the hyperbola satisfying the given conditions : Foci (0, ± 13), the conjugate axis is of length 24. Answer.
Given, foci (0, ± 13), the conjugate axis is of length 24.
Here, the foci are on the y-axis.
Therefore, the equation of the hyperbola is of the form \(\frac{y^{2}}{a^{2}}-\frac{x^{2}}{b^{2}}\) = 1.
a b2
Since the foci are (0, ± 13), c = 13.
Since the length of the conjugate axis is 24, 2b = 24
⇒ b = 12.
We know that a² + b² = c².
a² + 12² = 13²
⇒ a² = 169 – 144 = 25
Thus, the equation of the hyperbola is \( \frac{y^{2}}{25}-\frac{x^{2}}{144}\) = 1.

Question 12.
Find the equation of the hyperbola satisfying the given conditions : Foci (± 3√5, 0), the latus rectum is of length 8.
Answer.

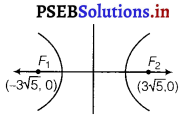
Here, foci at (± 3√5, 0)
∴ (± c, 0) = (± 3√5, 0)
⇒ c = 3√5
Length of latus rectum = \(\frac{2 b^{2}}{a}\) = 8 [given]
∴ b² = 4a …………….(i)
We know that, c² = a² + b²
⇒ (3√5)² = a² + 4a [put c = 3√5]
⇒ a = – 9, a = 5
∴ a = 5 as a cannot be negative.
On putting a = 5 in eq. (i), we get
b² = 5 × 4
⇒ b² = 20
Since, foci lies on X-axis, therefore the equation of hyperbola is of the form
\(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) = 1

i.e., \(\frac{x^{2}}{25}-\frac{y^{2}}{20}\) = 1 [Put a² = 5 and b² = 20]
⇒ 20x² – 25y² = 500
⇒ 4x² – 5y² = 100 [dividing both sides by 5]
which is required equation of hyperbola.

Question 13.
Find the equation of the hyperbola satisfying the given conditions : Foci (± 4, 0), the latus rectum is of length 12.
Answer.
Given, foci (± 4, 0), the latus rectum axis is of length 12.
Here, the foci are on the x-axis.
Therefore, the equation of the hyperbola is of the form \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) = 1.
Since the foci are (± 4, 0), c = 4.
Length of latus rectum =12
⇒ \(\frac{2 b^{2}}{a}\) = 12
⇒ b² = 6a
We know that a² + b² = c².
a² + 6a = 16
⇒ a² + 6a – 16 = 0
⇒ a² + 8a – 2a – 16 = 0
⇒ (a + 8) (a – 2) = 0
⇒ a = – 8, 2
Since a is non-negative, a = 2.
b² = 6a = 6 × 2 = 12
Thus, the equation of the hyperbola is \(\frac{x^{2}}{4}-\frac{y^{2}}{12}\) = 1.

Question 14.
Find the equation of the hyperbola satisfying the given conditions : Vertices (± 7, 0), e = \(\frac{4}{3}\).
Answer.
Given, vertices (± 7, 0), e = \(\frac{4}{3}\).
Here, the foci are on the x-axis.
Therefore, the equation of the hyperbola is of the form \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) = 1.
Since the vertices are (± 7, 0), a = 7.

Question 15.
Find the equation of the hyperbola satisfying the given conditions : Foci (0, ± √10), passing through (2, 3).
Answer.
Since, the foci (0, ± √10) are along Y-axis, then equation of hyperbola is of the form

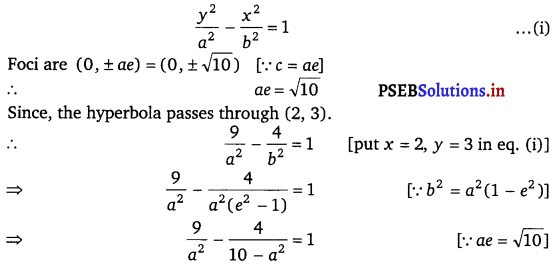
9(10 – a²) – 4a² = a²(10 – a²)
⇒ 90 – 13a² = 10a² – a⁴
⇒ a⁴ – 23a² + 90 = a
⇒ (a² – 18) (a² – 5) = 0
∴ a² = 18 or 5
Since, e = \(\frac{\sqrt{10}}{a}\) and e > 1
∴ \(\frac{\sqrt{10}}{a}\) > 1
⇒ a < √10; a² < 10
we reject a² = 18
Thus, a² = 5
∴ b² = a² e² – a²
= 10 – 5 = 5
Hence, equation of hyperbola is \(\frac{y^{2}}{5}-\frac{x^{2}}{5}\) = 1 [put a² = b² = 5]
or y² – x² = 5.