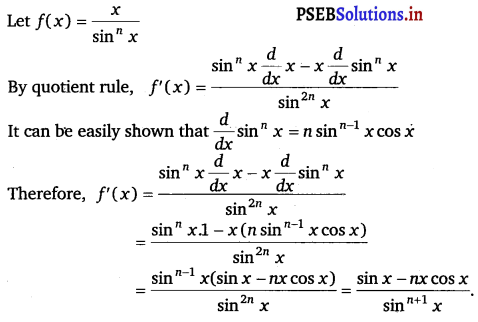PSEB 11th Class Maths Solutions Chapter 13 Limits and Derivatives Miscellaneous Exercise

Punjab State Board PSEB 11th Class Maths Book Solutions Chapter 13 Limits and Derivatives Miscellaneous Exercise Questions and Answers.

PSEB Solutions for Class 11 Maths Chapter 13 Limits and Derivatives Miscellaneous Exercise

Question 1.
Find the derivative of the following functions from first principle:
(i) – x
(ii) (- x)^{– 1}
(iii) sin (x + 1)
(iv) cos (x – \(\frac{\pi}{8}\))
Answer.
(i) Let f(x) = – x. Accordingly, f(x + h) = – (x + h)
By first prinicple,
f’(x) = \(\lim -{h \rightarrow 0} \frac{f(x+h)-f(x)}{h}\)

= \(\lim -{h \rightarrow 0} \frac{-(x+h)-(-x)}{h}\)

= \(\lim -{h \rightarrow 0} \frac{-x-h+x}{h}=\lim -{h \rightarrow 0} \frac{-h}{h}\)

= \(\lim -{h \rightarrow 0}\) (- 1) = – 1.

(ii) Let f(x) = (- x)^{– 1} = \(=\frac{1}{-x}=\frac{-1}{x}\)
Accordingly, f(x + h) = =\frac{1}{-x}=\frac{-1}{x}
By first prinicple,

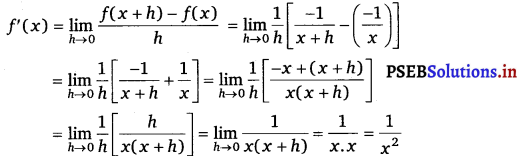
(iii) Let f(x) = sin (x +1).
Accordingly, f(x + h) = sin (x + h + 1)
By first prinicple,
f’(x) = \(\lim -{h \rightarrow 0} \frac{f(x+h)-f(x)}{h}\)

= \(\lim -{h \rightarrow 0} \frac{1}{h}\) [sin (x + h + 1) – sin (x + 1)]

= \(\lim -{h \rightarrow 0} \frac{1}{h}\left[2 \cos \left(\frac{x+h+1+x+1}{2}\right) \sin \left(\frac{x+h+1-x-1}{2}\right)\right]\)

(iv) Let f(x) = cos (x – \(\frac{\pi}{8}\))
By using first principle of derivative,
We have,
f'(x) = \(\lim -{h \rightarrow 0} \frac{f(x+h)-f(x)}{h}\)

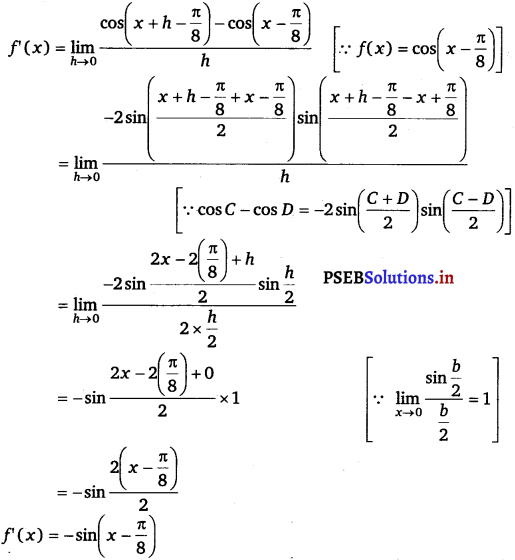
Question 2.
Find the derivative of the following functions (it is to be understood that a, b, e, d, p, q, r and s are fixed non-zero constants and m and n are integers): (x + a)
Answer.
Let f(x) = x + a.
Accordingly, f(x + h) = x + h + a
By first prinicple,
f’(x) = \(\lim -{h \rightarrow 0} \frac{f(x+h)-f(x)}{h}\)

= \(\lim -{h \rightarrow 0} \frac{x+h+a-x-a}{h}=\lim -{h \rightarrow 0}\left(\frac{h}{h}\right)\)

= \(\lim -{h \rightarrow 0}\) (1) = 1.

Question 3.
(Px + q) (\(\frac{r}{x}\) + s).
Answer.
Let f(x) = (Px + q) (\(\frac{r}{x}\) + s)
By Leibnitz product rule,
f’(x) = (px + q) (\(\frac{r}{x}\) + s) + (\(\frac{r}{x}\) + s) (px + q)’
= (px + q)(rx^{– 1} + s)’ + (\(\frac{r}{x}\) + s) (p)
= (px + q) (- rx^{– 2}) + (\(\frac{r}{x}\) + s) p
= (px + q) \(\left(\frac{-r}{x^{2}}\right)\) + (\(\frac{r}{x}\) + s) p
= \(\frac{-p r}{x}-\frac{q r}{x^{2}}+\frac{p r}{x}\) + ps
= ps – \(\frac{q r}{x^{2}}\).

Question 4.
(ax + b) (cx + d)².
Answer.
Let f(x) = (ax + b) (cx + d)²
By Leibnitz product rule,
f(x) = (ax + b) \(\frac{d}{d x}\) (cx + d)² + (cx + d)² \(\frac{d}{d x}\) (ax + b)
= (ax + b) \(\frac{d}{d x}\) (c²x² + 2cdx + d²) + (cx + d)² \(\frac{d}{d x}\) (ax + b)
= (ax + b) [\(\frac{d}{d x}\) (c²x²) + \(\frac{d}{d x}\) (2cdx) + \(\frac{d}{d x}\) d²] + (cx + d)² [\(\frac{d}{d x}\) ax + \(\frac{d}{d x}\) b]
= (ax + b) (2c²x + 2cd) + (cx + d²) a
= 2c (ax + b) (cx+ d) + a (cx + d)².

Question 5.
\(\frac{a x+b}{c x+d}\)
Answer.

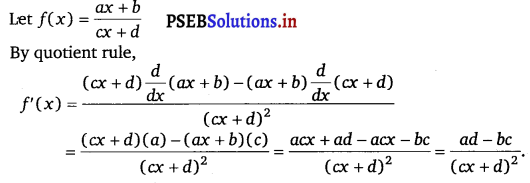
Question 6.
\(\frac{1+\frac{1}{x}}{1-\frac{1}{x}}\)
Answer.

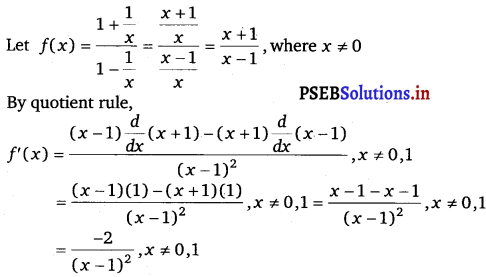
Question 7.
\(\frac{1}{a x^{2}+b x+c}\)
Answer.
Let f(x) = \(\frac{1}{a x^{2}+b x+c}\)
By quotient rule,
f'(x) = \(\frac{\left(a x^{2}+b x+c\right) \frac{d}{d x}(1)-\frac{d}{d x}\left(a x^{2}+b x+c\right)}{\left(a x^{2}+b x+c\right)^{2}}\)

= \(\frac{\left(a x^{2}+b x+c\right)(0)-(2 a x+b)}{\left(a x^{2}+b x+c\right)^{2}}\)

= \(\frac{-(2 a x+b)}{\left(a x^{2}+b x+c\right)^{2}}\)

Question 8.
\(\frac{a x+b}{p x^{2}+q x+r}\)
Answer.

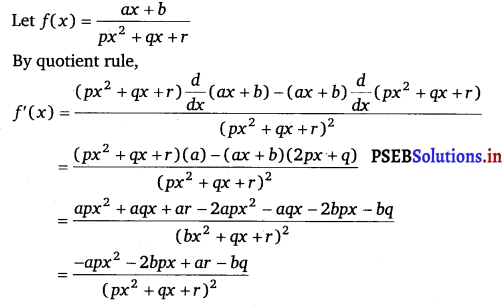
Question 9.
\(\frac{p x^{2}+q x+r}{a x+b}\)
Answer.

Question 10.
\(\frac{a}{x^{4}}-\frac{b}{x^{2}}\) + cos x
Answer.

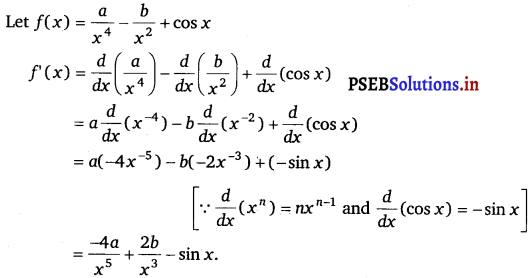
Question 11.
4√x – 2
Answer.
Let f(x) = 4√x – 2
f'(x) = \(\frac{d}{d x}\) (4√x – 2)
= \(\frac{d}{d x}\) (4√x) – \(\frac{d}{d x}\) (2)
= 4 \(\frac{d}{d x}\) (x^{\(\frac{1}{2}\)}) – 0
= 4 \(\left(\frac{1}{2} x^{\frac{1}{2}-1}\right)\)
= \(\left(2 x^{-\frac{1}{2}}\right)=\frac{2}{\sqrt{x}}\)

Question 12.
(ax + b)ⁿ
Answer.
Let f(x) = (ax + b)ⁿ
Accordingly, f(x + h) = {a(x + h) + b}ⁿ
= (ax + ah + b)ⁿ
By first principle,
f'(x) = \(\lim -{h \rightarrow 0} \frac{f(x+h)-f(x)}{h}\)

= \(\lim -{h \rightarrow 0} \frac{(a x+a h+b)^{n}-(a x+b)^{n}}{h}\)

Question 13.
(ax + b)ⁿ (cx + d)^m.
Answer.
Let f(x) = (ax + b)ⁿ (cx + d)^m
By Leibnitz product rule,

= \(\frac{m c(c x+d)^{m}}{(c x+d)}\)

= mc (cx + d)^{m – 1}
\(\frac{d}{d x}\) (cx + d)^m = mc (cx + d)^{m – 1} …………….(ii)
Similarly, (ax + b)ⁿ = na(ax + b)^{n – 1} ………….(iii)
Therefore, from eqs. (i), (ii) and (iii), we obtain
f'(x) = (ax + b)ⁿ {mc (cx + d)^{m – 1}} + (cx + d)^m {na(ax + b)^{n – 1}}
= (ax + b)^{n – 1} (a + d)^{m – 1} [mc (ax + b) + na (cx + d)].

Question 14.
sin (x + a).
Answer.
Let f(x) = sin (x + a), f(x + h) = sin (x + h + a)
By first principle,

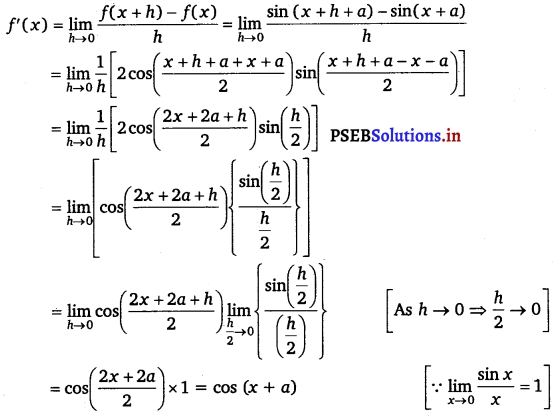
Question 15.
cosec x cot x
Answer.
Let f(x) = cosec x cot x
By Leibnitz product rule,
f’(x) = cosec x(cot x’ + cot x (cosec x)’ ……………(i)
Let f₁(x) = cot x,
Accordingly, f₁(x + h) = cot(x + h)
By first prinicple,
f₁‘(x) = \(\lim -{h \rightarrow 0} \frac{f-{1}(x+h)-f-{1}(x)}{h}\)

= \(\lim -{h \rightarrow 0} \frac{\cot (x+h)-\cot x}{h}\)

= \(\lim -{h \rightarrow 0} \frac{1}{h}\left(\frac{\cos (x+h)}{\sin (x+h)}-\frac{\cos x}{\sin x}\right)\)

Question 16.
\(\frac{\cos x}{1+\sin x}\)
Answer.

Question 17.
\(\frac{\sin x+\cos x}{\sin x-\cos x}\)
Answer.

Question 18.
\(\frac{\sec x-1}{\sec x+1}\)
Answer.
Let f(x) = \(\frac{\sec x-1}{\sec x+1}\)

Question 19.
sinⁿ x.
Ans.
Let y = sinⁿ x
Accordingly, for n = 1, y = sin x.
∴ \(\frac{d y}{d x}\) = cos x, i.e., \(\frac{d}{d x}\) sin x = cos x
For n = 2, y = sin² x
∴ \(\frac{d y}{d x}\) = \(\frac{d}{d x}\) (sin x sin x)
= (sin x)’ sin x + sin x (sin x)’ [by Leibnitz product rule]
= cos x sin x + sin x cos x
= 2 sin x cos x ………………..(i)
For n = 3, y = sin³ x
∴ \(\frac{d y}{d x}\) = \(\frac{d}{d x}\) (sin x sin² x)
= (sin x)’ sin² x + sin x (sin² x)’ [by Leibnitz product rule]
= cos x sin² x + sin x(2 sin x cos x) [using eq. (i)]
= cos x sin² x + 2 sin² x cos x
= 3 sin² x cos x
We assert that \(\frac{d}{d x}\) (sinⁿ x) = n sin^{(n – 1)} x cos x
Let our assertion be true for n = k.
ie., \(\frac{d}{d x}\) (sin^k x) = k sin^{(k – 1)} x cos x …………….(ii)
Consider, (sin^{k + 1} x) = \(\frac{d}{d x}\) (sin x sin^k x)
= (sin x)’ sin^k x + sin x (sin^k x)’ [by Leibnitz product rule]
= cos x sin^k x + sin x (k sin^{(k – 1)} x cos x) [using eq. (ii)]
= cos x sin^k x + k sin^k x cos x
= (k + 1) sin^k x cos x
Thus, our assertion is true for n = k + 1.
Hence, by mathematical induction, \(\frac{d}{d x}\) (sinⁿ x) = n sin^{(n – 1)} x cos x.

Question 20.
\(\frac{a+b \sin x}{c+d \cos x}\)
Answer.

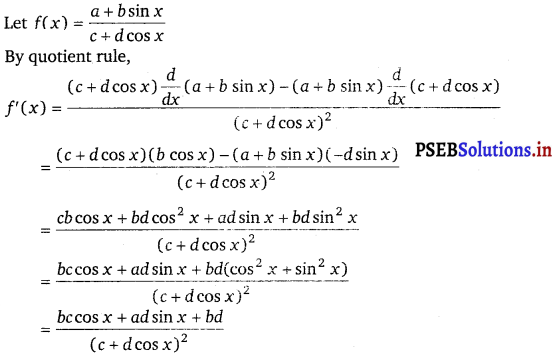
Question 21.
\(\frac{\sin (x+a)}{\cos x}\)
Answer.

Question 22.
x⁴ (5 sin x – 3 cos x)
Answer.
Let f(x) = x⁴ (5 sin x – 3 cos x)
By product rule,
f’(x) = x⁴ \(\frac{d}{d x}\) (5 sin x – 3 cos x) + (5 sin x – 3 cos x) \(\frac{d}{d x}\) (x⁴)
= x⁴ [5 \(\frac{d}{d x}\) (sin x) – 3 (cos x)] + (5 sin x – 3 cos x) (4x³)
= x⁴[5 cos x – 3(- sin x)] + (5 sin x – 3 cos x) (4x³)
= x³ [ 5x cos x + 3x sin x +20 sin x – 12 cos x].

Question 23.
(x² + 1) cos x.
Answer.
Let f(x) = (x² + 1) cos x
By product rule,
f’(x) = (x² + 1) \(\frac{d}{d x}\) (cos x) + cos x \(\frac{d}{d x}\) (x² + 1)
= (x² + 1) (- sin x) + cos x (2x)
= – x² sin x – sin x + 2x cos x.

Question 24.
(ax² + sin x) (p + q cos x).
Answer.
Let f(x) = (ax² + sin x) (p + q cos x)
By product rule,
f’(x) = (ax² + sin x) (p + q cos x) + (p + q cos x) (ax² + sin x)
= (ax² + sin x)(- q sin x) + (p + q cos x)(2ax + cos x)
= – q sin x (ax² + sin x) + (p + q cos x) (2ax + cos x).

Question 25.
(x + cos x) (x – tan x).
Answer.
Let y = (x + cos x) (x – tan x)
On differentiating both sides w.r.t. x, we get
ciy d d
= (x + cos x) . \(\frac{d}{d x}\) (x – tan x) + (x – tan x) (x + cos x)
[∵ \(\frac{d}{d x}\) (u . v) = u \(\frac{d v}{d x}\) + v \(\frac{d u}{d x}\)]
= (x + cos x) (1 – sec² x) + (x – tan x) (1 – sin x)
= (x + cos x) (- tan 2x) + (x – tan x) (1 – sin x)

Question 26.
\(\frac{4 x+5 \sin x}{3 x+7 \cos x}\)
Answer

Question 27.
\(\frac{x^{2} \cos \left(\frac{\pi}{4}\right)}{\sin x}\)
Answer.
Let f(x) = \(\frac{x^{2} \cos \left(\frac{\pi}{4}\right)}{\sin x}\)

By quotient rule, f'(x) = \(\cos \frac{\pi}{4} \cdot\left[\frac{\sin x \frac{d}{d x}\left(x^{2}\right)-x^{2} \frac{d}{d x}(\sin x)}{\sin ^{2} x}\right]\)

= \(\cos \frac{\pi}{4} \cdot\left[\frac{\sin x \cdot 2 x-x^{2} \cos x}{\sin ^{2} x}\right]\)

= \(\frac{x \cos \frac{\pi}{4}[2 \sin x-x \cos x]}{\sin ^{2} x}\)

Question 28.
\(\frac{x}{1+\tan x}\)
Answer.

Question 29.
(x + secx)(x-tanx).
Answer.
Let f(x) = (x + sec x) (x – tan x)
By product rule,
f’(x) = (x + sec x) \(\frac{d}{d x}\) (x – tan x) + (x – tan x) \(\frac{d}{d x}\) (x + sec x)
= (x + sec x) [\(\frac{d}{d x}\) (x) – \(\frac{d}{d x}\) tan x] + (x – tan x) [\(\frac{d}{d x}\) (x) + \(\frac{d}{d x}\) sec x]
= (x + sec x) [1 – \(\frac{d}{d x}\) tan x] + (x – tan x) [1 + \(\frac{d}{d x}\) sec x] ……………..(i)
Let f₁(x) = tan x, f₂(x) = sec x
Accordingly, f₁ (x + h) = tan (x + h) and f₂ (x + h) = sec (x + h)

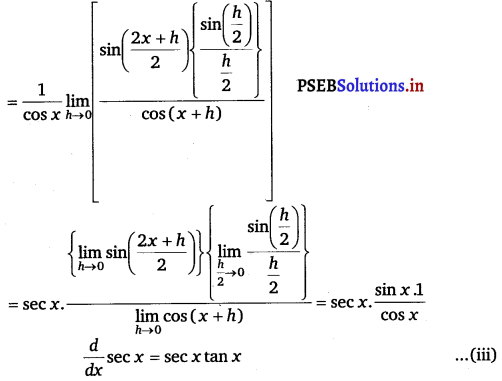
From eqs. (i), (ii) and (iii), we obtain
f'(x) = (x + sec x) (1 – sec² x) + (x – tan x)(1 + sec x tan x).

Question 30.
\(\frac{x}{\sin ^{n} x}\)
Answer.