PSEB 11th Class Maths Solutions Chapter 3 Trigonometric Functions Miscellaneous Exercise

Punjab State Board PSEB 11th Class Maths Book Solutions Chapter 3 Trigonometric Functions Miscellaneous Exercise Questions and Answers.

PSEB Solutions for Class 11 Maths Chapter 3 Trigonometric Functions Miscellaneous Exercise

Question 1.
Prove that:
\(2 \cos \frac{\pi}{13} \cos \frac{9 \pi}{13}+\cos \frac{3 \pi}{13}+\cos \frac{5 \pi}{13}\) = 0
Answer.

Hence proved.

Question 2.
Prove that: (sin 3x + sin x) sin x + (cos 3x – cos x) cos x = 0.
Answer.
L.H.S. = (sin 3x + sin x) sin x + (cos 3x – cos x) cos x
= sin 3x sin x + sin² x + cos 3x cos x – cos² x
= cos 3x cos x + sin 3x sin x – (cos² x – sin² x)
= cos (3x – x) – cos 2x
[∵ cos(A – B) = cos A cos B + sin A sin B]
= cos 2x – cos 2x = 0
=R.H.S.
Hence proved.

Question 3.
Prove that:
Answer.
L.H.S.= (cos x + cos y)² + (sin x – sin y)²
= cos² x + cos² y + 2 cos x cos y + sin² x + sin² y – 2 sin x sin y
= (cos² x + sin² x) + (cos² y + sin² y) + 2 (cos x cos y – sin x sin y)
= 1 + 1 + 2 cos (x + y)
[∵ cos (A + B) = (cos A cos B – sin A sin B)]
= 2 + 2 cos (x + y)
= 2 [1 + cos (x + y)]
= 2[1 + \(2 \cos ^{2}\left(\frac{x+y}{2}\right)\) – 1]
[∵ cos 2A = 2 cos² A – 1]
= 4 c0s² \(\left(\frac{x+y}{2}\right)\)
= R.H.S.
Hence proved.

Question 4.
Prove that:
(cos x – cos y)² + (sin x – sin y)² = 4 sin² \(\frac{x-y}{2}\)
Answer.
L.H.S.= (cos x – cos y)² + (sin x – sin y)²
= cos² x + cos² y – 2 cos x cos y + sin² x + sin² y – 2 sin x sin y
= (cos² x + sin² x) + (cos² y + sin² y) – 2 [cos x cos y + sin x sin y]
= 1 + 1 – 2 [cos (x – y)]
= 2 [1 – {1 – 2 sin² \(\left(\frac{x-y}{2}\right)\)}]
[∵ cos 2A = 1 – 2 sin² A]
= 4 sin² \(\left(\frac{x-y}{2}\right)\)
= R.H.S.
Hence proved.

Question 5.
Prove that: sin x + sin 3x + sin 5x + sin 7x = 4 cos x cos 2x sin 4x
Answer.
It is known that sin A + sin B = 2 \(\sin \left(\frac{A+B}{2}\right) \cdot \cos \left(\frac{A-B}{2}\right)\)
∴ L.H.S. = (sin x + sin 3x) + (sin 5x + sin 7x)
= (sin x + sin 5x) + (sin 3x + sin 7x)
= \(2 \sin \left(\frac{x+5 x}{2}\right)\) . \(\cos \left(\frac{x-5 x}{2}\right)+2 \sin \left(\frac{3 x+7 x}{2}\right) \cos \left(\frac{3 x-7 x}{2}\right)\)
= 2 sin 3x cos (- 2x) + 2 sin 5x cos (- 2x)
= 2 sin 3x cos 2x + 2 sin 5x cos 2x
= 2 cos 2x [sin 3x + sin 5x]
= 2 cos 2x [latex]2 \sin \left(\frac{3 x+5 x}{2}\right) \cdot \cos \left(\frac{3 x-5 x}{2}\right)[/latex]
= 2 cos 2x [2 sin 4x . cos (- x)]
= 4 cos 2x sin 4x cos x
= R.H.S.
Hence proved.

Question 6.
Prove that: \(\frac{(\sin 7 x+\sin 5 x)+(\sin 9 x+\sin 3 x)}{(\cos 7 x+\cos 5 x)+(\cos 9 x+\cos 3 x)}\) = tan 6x
Answer.
It is known that

Hence proved.

Question 7.
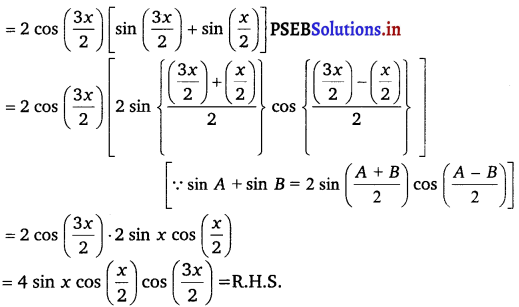
Prove that: sin 3x + sin 2x – sin x = 4 sin x cos \(\frac{x}{2}\) cos \(\frac{3 x}{2}\).
Answer.
L.H.S. = sin 3x + sin 2x – sin x
= sin 3x + (sin 2x – sin x)

Question 8.
Find sin \(\frac{x}{2}\), cos \(\frac{x}{2}\) and tan \(\frac{x}{2}\) for tan x = – \(\frac{4}{3}\), x in quadrant II.
Answer.

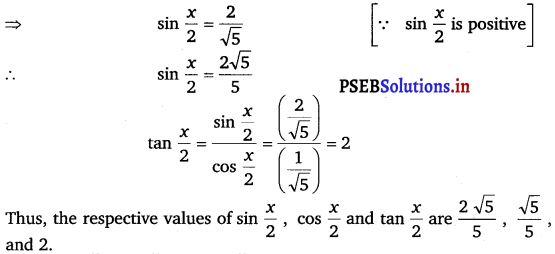
Question 9.
Find sin \(\frac{x}{2}\), cos \(\frac{x}{2}\) and tan \(\frac{x}{2}\) for cos x = – \(\frac{1}{3}\), x in quadrant III.
Answer.

Thus, the respective values of sin \(\frac{x}{2}\), cos \(\frac{x}{2}\) and tan \(\frac{x}{2}\) are \(\frac{\sqrt{6}}{5}\), \(\frac{\sqrt{3}}{3}\) and – √2.

Question 10.
Find sin \(\frac{x}{2}\), cos \(\frac{x}{2}\) and tan \(\frac{x}{2}\) for sin x = \(\frac{1}{4}\), x in quadrant II.
Answer.

Thus, the respective values of sin \(\frac{x}{2}\), cos \(\frac{x}{2}\) and tan \(\frac{x}{2}\) are \(\sqrt{\frac{8+2 \sqrt{15}}{4}}\), \(\sqrt{\frac{8-2 \sqrt{15}}{4}}\) and 4 + √15.