PSEB 11th Class Maths Solutions Chapter 5 Complex Numbers and Quadratic Equations Ex 5.2

Punjab State Board PSEB 11th Class Maths Book Solutions Chapter 5 Complex Numbers and Quadratic Equations Ex 5.2 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 11 Maths Chapter 5 Complex Numbers and Quadratic Equations Ex 5.2

Question 1.
Find the modulus and the argument of the complex number z = – 1 – i√3
Answer.

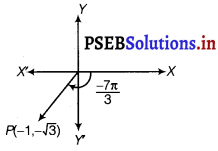
We have, z = – 1 – i√3
Let – 1 – i√3 = r (cos θ + i sin θ)
On equating real and imaginary parts both sides, we get
r cos θ = – 1 …………….(i)
and r sin θ = – √3 ……………(ii)
On squaring and adding eqs. (i) and (ii) we get
r² (cos² θ + sin² θ) = 1 + 3
⇒ r² = 4
∴ r = 2 [taking positive square root]
Modulus of z, |z| = r = 2
On putting the value of r in eqs. (i) and (ii), we get
cos θ = – \(\frac{1}{2}\) and
sin θ = \(\frac{-\sqrt{3}}{2}\)
Since, both cos θ and sin θ are negative.
So, θ lies in III quadrant.
θ = – (π – \(\frac{\pi}{3}\))
= \(-\frac{2 \pi}{3}\)
Hence, the modulus and argument of the complex number – 1 – i√3 are 2 and \(-\frac{2 \pi}{3}\) respectively.

Question 2.
Find the modulus and the argument of the complex number
z = – √3 + i.
Answer.

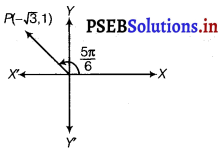
z = – √3 + i
Let r cos θ = – √3 and r sin θ = 1
On squaring and adding, we obtain
⇒ r² cos² θ + r² sin² θ = (- √3)² + 1²
⇒ r² = 3 + 1 = 4 [∵ cos² θ + sin² θ = 1]
⇒ r = √4 = 2 [Conventionally, r > 0]
∴ Modulus = 2
∴ 2 cos θ = – √3 and 2 sin θ = 1
cos θ = \(\frac{-\sqrt{3}}{2}\) and sin θ = \(\frac{1}{2}\)
∴ θ = π – \(\frac{\pi}{6}\)
= \(\frac{5 \pi}{6}\) [As θ lies in the II quadrant]
Thus, the modulus and argument of the complex number – √3 + i are 2 and \(\frac{5 \pi}{6}\) respectively.

Question 3.
Convert the given complex number in polar form : 1 – i.
Answer.
1 – i
Let r cos θ = 1 and r sin θ = – 1
On squaring and adding, we obtain r² cos² θ + r² sin² θ = 1² + (- 1)²
⇒ r² (cos² θ + sin² θ) = 1 + 1
⇒ r² = 2
⇒ r =√2 [Conventionally, r > 0]
∴ √2 cos θ = 1 and √2 sin θ = – 1
⇒ cos θ = \(\frac{1}{\sqrt{2}}\) and sin θ = – \(\frac{1}{\sqrt{2}}\)
∴ θ = \(-\frac{\pi}{4}\) [As θ lies in the IV quadrant]
∴ 1 – i = r cos θ + ir sin θ = √2 \(\cos \left(-\frac{\pi}{4}\right)+i \sqrt{2} \sin \left(-\frac{\pi}{4}\right)\)

= √2 \(\left[\cos \left(-\frac{\pi}{4}\right)+i \sin \left(-\frac{\pi}{4}\right)\right]\)
This is the required polar form.

Question 4.
Convert the given complex number in polar form : – 1 + i
Answer.
– 1 + i
Let r cos θ = – 1 and r sin θ = 1
On squaring and adding, we obtain
r² cos² θ + r² sin² θ = (- 1)² + 1²
⇒ r² (cos² θ + sin² θ) = 1 + 1
⇒ r² = 2
⇒ r = √2 [Conventionally, r > 0]
∴ √2 cos θ = – 1 and √2 sin θ = 1
⇒ cos θ = – \(\frac{1}{\sqrt{2}}\) = and sin θ = – \(\frac{1}{\sqrt{2}}\)

∴ θ = – (π – \(\frac{\pi}{4}\)) = \(-\frac{3 \pi}{4}\) [As θ lies in the III quadrant]
∴ – 1 – i = r cos θ + ir sin θ
= √2 cos \(-\frac{3 \pi}{4}\) + i √2 sin \(-\frac{3 \pi}{4}\)

= √2 (cos \(-\frac{3 \pi}{4}\) + isin \(-\frac{3 \pi}{4}\))

This is the required polar form.

Question 6.
Convert the given complex number in polar form : – 3
Answer.
– 3
Let r cos θ = – 3 and r sin θ = 0
On squaring and adding, we obtain
r² cos² θ + r² sin² θ = (- 3)²
r² (cos² θ + sin² θ) = 9
r = √9 = 3 [Conventionally, r > 0]
∴ 3 cos θ = – 3 and 3 sin θ = 0
cos θ = – 1 and sin θ = 0
∴ θ = π
∴ – 3 = r cos θ + ir sin θ = 3 cos π + i3 sin π
= 3 (cos π + i sin π)
This is the required polar form.

Question 7.
Convert the given complex number in polar form : √3 + i.
Answer.
√3 + i
Let r cos θ = √3 and r sin θ =1
On squaring and adding, we obtain
r² cos² θ + r² sin² θ
= (√3)² + 1²
r² (cos² θ + sin² θ) = 3 + 1
r² = 4
r = √4 = 2 [Conventionally, r > 0]
∴ 2 cos θ = √3 and 2 sin θ = 1

⇒ cos θ = \(\frac{\sqrt{3}}{2}\) and sin θ = \(\frac{1}{2}\)

∴ θ = \(\frac{\pi}{6}\) [As θ lies in yhe I quadrant]

∴ √3 + i = r cos θ + i r sin θ
= 2 cos \(\frac{\pi}{6}\) + i sin \(\frac{\pi}{6}\)
= 2 (cos \(\frac{\pi}{6}\) + i sin \(\frac{\pi}{6}\))
This is the required polar form.

Question 8.
Convert the given complex number in polar form: i.
Answer.
Let r cos θ = 0 and r sin θ = 1
On squaring and adding, we obtain
r² cos² θ + r² sin² θ = 0² + 1²
r² (cos² θ + sin² θ) = 1
r² = 1
r = √i = 1 [Conventionally, r> 0]
∴ cos θ = 0 and sin θ = 1
∴ θ = \(\frac{\pi}{2}\)
∴ i = r cos θ +1 r sin θ
= cos \(\frac{\pi}{2}\) + sin \(\frac{\pi}{2}\)
This is the required polar form.