PSEB 11th Class Maths Solutions Chapter 5 Complex Numbers and Quadratic Equations Miscellaneous Exercise

Punjab State Board PSEB 11th Class Maths Book Solutions Chapter 5 Complex Numbers and Quadratic Equations Miscellaneous Exercise Questions and Answers.

PSEB Solutions for Class 11 Maths Chapter 5 Complex Numbers and Quadratic Equations Miscellaneous Exercise

Question 1.
Evaluate \(\left[i^{18}+\left(\frac{1}{i}\right)^{25}\right]^{3}\).
Answer.

= – [1³ + i³ + 3 . 1 – i (1 + i)]
= – [1 + i³ + 3i + 3i²]
= – [1 – i + 3i – 3]
= – [- 2 + 2i]
=2 – 2 i.

Question 2.
For any two complex numbers z₁ and z₂, prove that Re (z₁z₂) = Re z₁ Re z₂ – Im z₁ Im z₂.
Answer.
Let z₁ = x₁ + iy₁ and
z₂ = x₂ + iy₂
∴ z₁z₂ = (x₁ + iy₁) (x₂ + iy₂)
= x₁ (x₂ + iy₂) + iy₁ (x₂ + iy₂)
= x₁x₂ + ix₁y₂ + iy₁x₂ + i²y₁y₂
= x₁x₂ + ix₁y₂ + iy₁x₂ – y₁y₂ [∵ i² = – 1]
= (x₁x₂ – y₁y₂) + i(x₁y₂ + y₁x₂)
Re (z₁z₂) = x₁x₂ – y₁y₂
Re (z₁z₂) = Re z₁ Re z₂ – Im z₁ Im z₂
Hence proved.

Question 3.
Reduce \(\left(\frac{1}{1-4 i}-\frac{2}{1+i}\right)\left(\frac{3-4 i}{5+i}\right)\) to the standard form.
Answer.

Question 4.
If x – iy = \(\sqrt{\frac{a-i b}{c-i d}}\) prove that (x² + y²)² = \(\frac{a^{2}+b^{2}}{c^{2}+d^{2}}\).
Answer.
We have, x – iy = \(\sqrt{\frac{a-i b}{c-i d}}\)
On squaring both sides, we get
x² – y² – 2 ixy = \(\frac{a-i b}{c-i d}\)

= \(\frac{a-i b}{c-i d} \times \frac{c+i d}{c+i d}\) [multiplying numerator and denominator by c + id]

Question 5.
Convert the following in the polar form.
(i) \(\frac{1+7 i}{(2-i)^{2}}\)

(ii) \(\frac{1+3 i}{1-2 i}\)
Answer.
z = \(\frac{1+7 i}{(2-i)^{2}}\)
(i) Here,

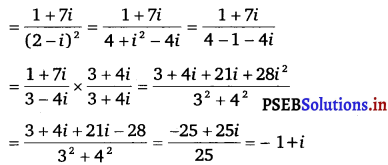
Let r cos θ = 1 and r sin θ = 1
On squaring and adding, we obtain
r² (cos² θ + sin² θ) = 1 + 1
r² (cos² θ + sin² θ) = 2
[∵ cos² θ + sin² θ = 1]
r² = 2 [Conventionally, r > 0]
r = √2
√2 cos θ = – 1 and sin θ = 1
cos θ = \(\frac{-1}{\sqrt{2}}\) and sin θ = \(\frac{1}{\sqrt{2}}\)
∴ θ = π – \(\frac{\pi}{4}\) [As θ lies in II quadrant]
= \(\frac{3 \pi}{4}\)

∴ z = r cos θ + i r sin θ
⇒ \(\sqrt{2} \cos \frac{3 \pi}{4}+i \sqrt{2} \sin \frac{3 \pi}{4}=\sqrt{2}\left(\cos \frac{3 \pi}{4}+i \sin \frac{3 \pi}{4}\right)\)

This is the required polar form.

(ii)

Question 6.
Solve the equation 3x² – 4x + \(\frac{20}{3}\) = 0.
Ans.
The given quadratic equation is 3x² – 4x + \(\frac{20}{3}\) = 0
This equation can also be written as 9x² – 12x + 20 = 0
On comparing this equation with ax² + bx + c = 0, we obtain
a = 9, b = – 12, and c = 20
Therefore, the discriminant of the given equation is
D = b² – 4aç
= (- 12)² – 4 × 9 × 20
= 144 – 720 = – 576
Therefor, the required solutions are
\(\frac{-b \pm \sqrt{D}}{2 a}=\frac{-(-12) \pm \sqrt{-576}}{2 \times 9}=\frac{12 \pm \sqrt{576} i}{18}\) [∵ √- 1 = i]

= \(\frac{12 \pm 24 i}{18}=\frac{6(2 \pm 4 i)}{18}\)

= \(\frac{2 \pm 4 i}{3}=\frac{2}{3} \pm \frac{4}{3} i\)

Question 7.
Solve the equation x² – 2x + \(\frac{3}{2}\) = 0
Ans.
The given quadratic equation is x² – 2x + \(\frac{3}{2}\) = 0
This equation can also be written as 2x² – 4x + 3 = 0
On comparing this equation with ax² + bx + c = 0, we obtain
a = 2, b = – 4, and c = 3
Therefore, the discriminant of the given equation is
D = b² – 4ac
= (- 4)² – 4 × 2 × 3
= 16 – 24 = -8
Therefore, the required solutions are
\(\frac{-b \pm \sqrt{D}}{2 a}=\frac{-(-4) \pm \sqrt{-8}}{2 \times 2}=\frac{4 \pm 2 \sqrt{2} i}{4}\) [∵ √- 1 = i]

= \(\frac{2 \pm \sqrt{2} i}{2}=1 \pm \frac{\sqrt{2}}{2} i\).

Question 8.
Solve the equation 27x² – 10x + 1 = 0
Answer.
The given quadratic equation is 27x² – 10x + 1 = 0
On comparing the given equation with ax² + bx + c = 0, we obtain
a = 27, b = – 10, and c = 1
Therefore, the discriminant of the given equation is
D = b² – 4ac
= (- 10)² – 4 × 27 × 1
= 100 – 108
= – 8
Therefore, the required solutions are
\(\frac{-b \pm \sqrt{D}}{2 a}=\frac{-(-10) \pm \sqrt{-8}}{2 \times 27}=\frac{10 \pm 2 \sqrt{2} i}{54}\) [∵ √- 1 = i]

= \(\frac{5 \pm \sqrt{2} i}{27}=\frac{5}{27} \pm \frac{\sqrt{2}}{27} i[/latex ]

Question 9.
Solve the equation 21x² – 28x + 10 = 0
Answer.
The given quadratic equation is 21x² – 28x + 10 = 0
On comparing the given equation with ax² + bx + c = 0, we obtain
a = 21, b = – 28, and c = 10 .
Therefore, the discriminant of the given equation is
D = b² – 4ac
= (- 28)² – 4 × 21 × 10
= 784 – 840 = – 56
Therefore, the required solutions are
[latex]\frac{-b \pm \sqrt{D}}{2 a}\) = \(\frac{-(-28) \pm \sqrt{-56}}{2 \times 21}\)

= \(\frac{28 \pm \sqrt{56} i}{42}\)

= \(\frac{28 \pm 2 \sqrt{14} i}{42}=\frac{28}{42} \pm \frac{2 \sqrt{14}}{42} i=\frac{2}{3} \pm \frac{\sqrt{14}}{21} i\).

Question 10.
If z₁ = 2 – i, z₂ = 1 + i, find \(\left|\frac{z_{1}+z_{2}+1}{z_{1}-z_{2}+1}\right|\).
Answer.

= \(\left|\frac{2(1+i)}{2}\right|\) = |1 + i|

= \(\sqrt{1^{2}+1^{2}}=\sqrt{2}\)

Thus the value of \(\left|\frac{z_{1}+z_{2}+1}{z_{1}-z_{2}+1}\right|\) is √2.

Question 11.
If a + ib = \(\frac{(x+i)^{2}}{2 x^{2}+1}\), prove that a² + b² = \(\frac{(x+1)^{2}}{(2 x+1)^{2}}\).
Answer.

Question 12.
Let z₁ = 2 – i₁, z₂ = – 2 + i
(i) Re (\(\frac{\boldsymbol{z}_{\mathbf{1}} \boldsymbol{z}_{\mathbf{2}}}{\overline{\boldsymbol{z}}_{\mathbf{1}}}\))

(ii) Im (\(\frac{1}{z_{1} \overline{\boldsymbol{z}}_{1}}\))
Answer.
z₁ = 2 – i, z₂ = – 2 + i,
(i) z₁z₂ = (2 – i) (- 2 + i)
= – 4 + 2i + 2i – i²
= – 4 + 4i – (- 1)
= – 3 + 4 i

(ii)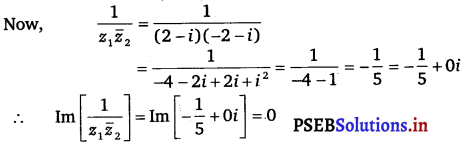

Question 13.
Find the modulus and argument of the complex number
Answer.

Question 14.
Find the real numbers x and y if (x – iy) (3 + 5i) is the conjugate of – 6 – 24i.
Answer.
We have, (x – iy)(3 + 5i) is the conjugate of – 6 – 24 i
⇒ (x – iy)(3 + 5i) = – 6 – 24i
[conjugate of – 6 – 24i = -6 + 24i]
⇒ 3x – 3iy + 5ix + 5y = – 6 + 24i
(3x + 5y) + i (5x – 3y ) = – 6 + 24i ………………(i)
On equating real and imaginary parts both sides of eq. (i), we get
3x + 5y = – 6 …………….(ii)
and 5x-3y = 24 …………..(iii)
On solving eqs. (ii) and (iii), we get
x = 3 and y = – 3.

Question 15.
Find the modulus of \(\frac{1+i}{1-i}\) – \(\frac{1-i}{1+i}\).
Answer.
\(\frac{1+i}{1-i}-\frac{1-i}{1+i}=\frac{(1+i)^{2}-(1-i)^{2}}{(1-i)(1+i)}\)

= \(\frac{1+i^{2}+2 i-1-i^{2}+2 i}{1^{2}+1}=\frac{4 i}{2}=2 i\)

∴ \(\left|\frac{1+i}{1-i}-\frac{1-i}{1+i}\right|=|2 i|=\sqrt{2^{2}}=2\).

Question 16.
If (x + iy)³ = u + iv, then show that \(\frac{u}{x}+\frac{v}{y}\) = 4 (x² – y²).
Answer.
(x + iy)³ = u + iv
x³ + (iy)³ + 3.x.iy (x + iy) = u + iv
= x³ + i³y³ + 3x²yi – 3xy²i² = u + iv
= x³ – iy³ + 3x²yi – 3xy² = u + iv
(x³ – 3xy²) + i(3x²y – y³) = u + iv
On equating real and imaginary parts, we obtain
u = x³ – 3xy², v = 3x²y – y³

∴ \(\frac{u}{x}+\frac{v}{y}=\frac{x^{3}-3 x y^{2}}{x}+\frac{3 x^{2} y-y^{3}}{y}\)

= \(\frac{x\left(x^{2}-3 y^{2}\right)}{x}+\frac{y\left(3 x^{2}-y^{2}\right)}{y}\)

= x² – 3y² + 3x² – y²
= 4x² – 4y²
= 4 (x² – y²)

∴ \(\frac{u}{x}+\frac{v}{y}\) = 4 (x² – y²).
Hence proved.

Question 17.
If α and β are different complex numbers with |β| = 1, then find \(\left|\frac{\beta-\alpha}{1-\bar{\alpha} \beta}\right|\).
Answer.
Let α = a + ib and β = x + iy
It is given that, |β| = 1
∴ \(\sqrt{x^{2}+y^{2}}\) = 1
∴ x² + y² = 1 ……………..(i)

= \(\frac{\sqrt{1+a^{2}+b^{2}-2 a x-2 b y}}{\sqrt{1+a^{2}+b^{2}-2 a x-2 b y}}\) [using eq. (i)]

= 1

∴ \(\left|\frac{\beta-\alpha}{1-\bar{\alpha} \beta}\right|\) = 1.

Question 18.
Find the number of non-zero integral solutions of the equation |1 – i|^x = 2^x.
Answer.
|1 – i|^x = 2^x
⇒ \(\left(\sqrt{1^{2}+(-1)^{2}}\right)^{x}\) = 2^x
⇒ (A/2)^x = 2^x
⇒ 2^{\(\frac{x}{2}\)} = 2^x
⇒ \(\frac{x}{2}\) = x
⇒ x = 2x
⇒ 2x – x = 0
⇒ x = 0
Thus, 0 is the only integral solution of the given equation. Therefore, the number of non-zero integral solutions of the given equation is 0.

Question 19.
If (a + ib) (c + id) (e + if) (g + ih) = A + iB, then show that (a² + b²) (c² + d²) (e² + f²) (g² + h²) = A² + B².
Answer.
(a + ib) (c + id) (e + if) (g + ih) = A + iB
∴ |(a + ib)(c + id)(e + if)(g + ih)| = |A + iB|
⇒ |(a + ib)| × |(c + id)| × |(e + if)| × |(g + ih)| = |A + iB| [v |z1z2|=|z1||z2|]
⇒ \(\sqrt{a^{2}+b^{2}} \times \sqrt{c^{2}+d^{2}} \times \sqrt{e^{2}+f^{2}} \times \sqrt{g^{2}+h^{2}}=\sqrt{A^{2}+B^{2}}\)
On squaring both sides, we obtain
(a² + b²) (c² + d²) (e² + f²) (g² + h²) = A² + B²
Hence proved.

Question 20.
If \(\left(\frac{1+i}{1-i}\right)^{m}\) = 1, then find the least positive integral value of m.
Solution.

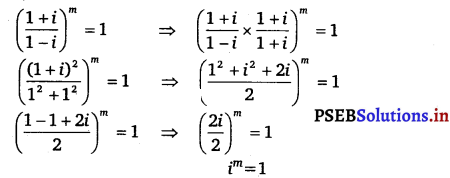
∴ m = 4k, where k is some integer.
Therefore, the least positive integer is 1.
Thus, the least positive integral value of m is 4 (= 4 × 1).