PSEB 11th Class Maths Solutions Chapter 8 Binomial Theorem Ex 8.2

Punjab State Board PSEB 11th Class Maths Book Solutions Chapter 8 Binomial Theorem Ex 8.2 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 11 Maths Chapter 8 Binomial Theorem Ex 8.2

Question 1.
Find the coefficient of x⁵ in (x + 3)⁸
Answer.
It is known that (r + 1)th term, (T_{r + 1}), in the binomial expansion of (a + b)ⁿ is given by T_{r + 1} = \({ }^{n} C_{r}\) a^{n – r} b^r
Assuming that x⁵ occurs in the (r + 1)th term of the expansion (x + 3)⁸, we obtain
T_{r + 1} = \({ }^{8} C_{r}\) (x)^{8 – r} (3)^r
Comparing the indices of x in x⁵ and in T_{r + 1}, we obtain r = 3.
Thus, the coefficient of x⁵ is \({ }^{8} C_{3}\) (3)³
= \(\frac{8 !}{3 ! 5 !} \times 3^{3}\)

= \(\frac{8 \cdot 7 \cdot 6 \cdot 5 !}{3 \cdot 2.5 !} \cdot 3^{3}\) = 1512.

Question 2.
Find the coefficient of a⁵ b⁷ in (a – 2b)¹².
Answer.
It is known that (r + 1)th term, (T_{r + 1}), in the binomial expansion of (a + b)ⁿ is given by T_{r + 1} = \(\) a^{n – r} b^r
Assuming that a⁵b⁷ occurs in the (r + 1)th term of the expansion (a – 2b)¹²,we obtain
T_{r + 1} = \({ }^{12} C_{r}\) (a)^{12 – r} (- 2b)^r
= \({ }^{12} C_{r}\) (- 2)^r (a)^{12 – r} (b)^r
Comparing the indices of a and b in a⁵b⁷ and in T_{r + 1}, we obtain r = 7
Thus, the coefficient of a⁵b⁷ is
12C7 (- 2)⁷ = \(\frac{12 !}{7 ! 5 !} \cdot 2^{7}\)
= \(-\frac{12.11 .10 .9 .8 .7 !}{5.4 .3 .2 .7 !} \cdot 2^{7}\)
= – (792) (128)
= – 101376

Question 3.
Write the general term ¡n the expansion of (x² – y)⁶.
Answer.
General term in the expansion of (a + b)ⁿ is given by
T_{r + 1} = \({ }^{n} C_{r}\) a^{n – r} b^r
T_{r + 1} = \({ }^{6} C_{r}\) (x²)^{6 – r} (y)^r
= \({ }^{6} C_{r}\) x^{12 – r} (- y)^r

Question 4.
Write the general term in the expansion of (x² – 2y)¹², x ≠ 0.
Answer.
It is known that the general term T_{r + 1} {which is the (r + 1)th term} in the binomial expansion of (a + b)ⁿ is given by T_{r + 1} = \({ }^{n} C_{r}\) a^{n – r} b^r
Thus, the general term in the expansion of (x² – yx)¹² is
T_{r + 1} = \({ }^{12} C_{r}\) (x²)^{12 – r} (- yx)^r
= (- 1)^r \({ }^{12} C_{r}\) x24-2r . y^r . x^r
= (- 1)^r \({ }^{12} C_{r}\) x^{24 – r} . y^r

Question 5.
Find the 4th term in the expansion of (x – 2y)¹².
Answer.
It is known that (r + 1)th term, (T_{r + 1}), in the binomial expansion of (a + b)ⁿ is given by T_{r + 1} = \({ }^{n} C_{r}\) a^{n – r} b^r
Thus, the 4th term in the expansion of (x – 2y)¹² is
T₄ = T_{3 + 1}
= \({ }^{12} C_{3}[/latex (x)^{12 – 3} (- 2y)³
= (- 1)³ . [latex]\frac{12 !}{3 ! 9 !}\) . x⁹ . (2)³ . y³
= – \(\frac{12 \cdot 11 \cdot 10}{3.2}\) . x⁹ . (2)³ . y³
= – 1760 x⁹ . x⁹ . y³

Question 6.
Find the 13th term in the expansion of (9x – \(\frac{1}{3 \sqrt{x}}\))¹⁸, x ≠ 0.
Answer.

Question 7.
Find the middle terms in the expansions of \(\left(3-\frac{x^{3}}{6}\right)^{7}\).
Answer.
It is known that in the expansion of (a + b)ⁿ, if n is odd, then there are two middle terms, namely \(\left(\frac{n+1}{2}\right)^{t h}\) term and \(\left(\frac{n+1}{2}+1\right)^{t h}\) term.

Therefore, the middle terms in the expansion of \(\left(3-\frac{x^{3}}{6}\right)^{7}\) are \(\left(\frac{7+1}{2}\right)^{t h}\)

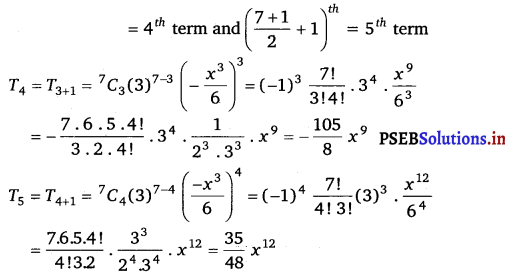
Thus, the middle terms in the expansion of \(\left(3-\frac{x^{3}}{6}\right)^{7}\) are – \(\frac{105}{8}\) x⁹ and \(\frac{35}{48}\) x¹².

Question 8.
Find the middle terms in the expansions of \(\left(\frac{x}{3}+9 y\right)^{10}\).
Answer.
It is known that in the expansion (a + b)ⁿ, if n is even, then the middle term is \(\left(\frac{n}{2}+1\right)^{t h}\) term.

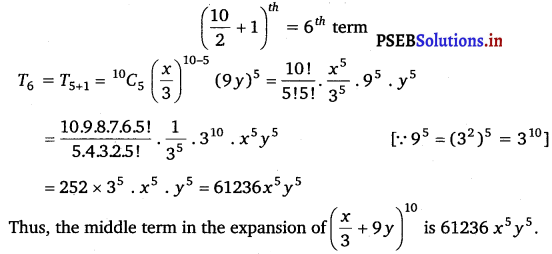
Therefore, the middle term in the expansion of \(\left(\frac{x}{3}+9 y\right)^{10}\) is 61236 x⁵ y⁵.

Question 9.
In the expansion of (1 + a)^{m + n}, prove that coefficients of a^m and aⁿ are equal.
Answer.
It is known that (r + 1)th term, (T_{r + 1}), in the binomial expansion of (a + b)ⁿ is given by
T_{r + 1} = \(\) a^{n – r} b^r.

Question 10.
The coefficients of the (r – 1)th, rth and (r + 1)th terms in the expansion of (x + 1)ⁿ are in the ratio 1 : 3 : 5. Find n and r.
Answer.

Question 11.
Prove that the coefficient of xⁿ in the expansion of (1 + x)²ⁿ is twice the coefficient of xⁿ in the expansion of (1 + x)^{2n – 1}.
Answer.

From eqs. (i) and (ii), it is observed that \(\frac{1}{2}{ }^{2 n} C_{n}={ }^{2 n-1} C_{n}\).

\({ }^{2 n} C_{n}=2\left({ }^{2 n-1} C_{n}\right)\)

Therefore, the coefficient of xⁿ in the expansion of (1 + x)²ⁿ is twice the coefficient of xⁿ in the expansion of (1 + x)^{2n – 1}.
Hence proved.

Question 12.
Find a positive value of m for which the coefficient of xⁿ in the expansion (1 + x)^m is 6.
Answer.
It is known that (r + 1)th term, (T_{r + 1}), in the binomial expansion of (a + b)ⁿ is given by T_{r + 1} = \(\) a^{n – r}b^r.

Assuming that x² occurs in the (r + 1)th term of the expansion (1 + x)^m, we obtain
\(T_{r+1}={ }^{m} C_{r}(1)^{m-r}(x)^{r}={ }^{m} C_{r}(x)^{r}\)

Comparing the indices of x in x² and in T_{r + 1}, we obtain r = 2
Therefore, the coefficient of x₂ is \({ }^{m} C_{2}\)

It is given that the coefficient of x² in the expansion (1 + x)^m is 6.

\({ }^{m} C_{2}\) = 6

⇒ \(\frac{m !}{2 !(m-2) !}\) = 6

⇒ \(\frac{m(m-1)(m-2) !}{2 \times(m-2) !}\) = 6
⇒ m (m – 1) = 12
⇒ m² – m – 12 = 0
⇒ m² – 4m + 3m – 12 = 0
⇒ m(m – 4) + 3(m – 4) = 0
⇒ (m – 4) (m + 3) = 0
⇒ (m – 4) = 0 or (m + 3) = 0
⇒ m = 4 or m = – 3.
Thus, the positive value of m, for which the coefficient of x² in the expansion (1 + x)^m is 6, is 4.