PSEB 11th Class Maths Solutions Chapter 9 Sequences and Series Ex 9.4

Punjab State Board PSEB 11th Class Maths Book Solutions Chapter 9 Sequences and Series Ex 9.4 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 11 Maths Chapter 9 Sequences and Series Ex 9.4

Question 1.
Find the sum to n terms of the series
1 × 2 + 2 × 3 + 3 × 4 + 4 × 5 + ……………
Answer.
Let S = 1 . 2 + 2 . 3 + 3 . 4 + 4 . 5 + …………….
Then, nth term,
T_n = n(n + 1) = n² + n
∴ T_n = n² + n
On taking summation from 1 to n on both sides we get

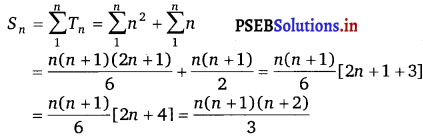
Question 2.
Find the sum to n terms of the series
1 × 2 × 3 + 2 × 3 × 4 + 3 × 4 × 5 + …………..
Answer.
The given series is 1 × 2 × 3 + 2 × 3 × 4 + 3 × 4 × 5 + …………..
nth term a_n = n (n + 1) (n + 2)
= (n² + n) (n + 2) = n² + 3n² + 2n

Question 3.
Find the sum of n terms of the series 3 × 1² + 5 × 2² + 7 × 3² + ……………..
Answer.
The given series is 3 × 1² + 5 × 2² + 7 × 3² + ……………..
nth term a_n = (2n + 1) n²
= 2n³ + n²
∴ S_n = \(\sum_{k=1}^{n} a_{k}=\sum_{k=1}^{n}\left(2 k^{3}+k^{2}\right)=2 \sum_{k=1}^{n} k^{3}+\sum_{k=1}^{n} k^{2}\)

= \(2\left[\frac{n(n+1)}{2}\right]^{2}+\frac{n(n+1)(2 n+1)}{6}\)

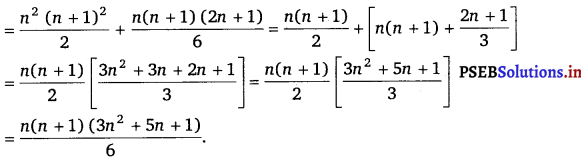
Question 4.
Fmd the sum to n terms of the series \(\frac{1}{1 \times 2}+\frac{1}{2 \times 3}+\frac{1}{3 \times 4}\) + …….
Answer.
Let the given series be
S = \(\frac{1}{1 \times 2}+\frac{1}{2 \times 3}+\frac{1}{3 \times 4}\) + …….
Then, nth term T_n = \(\frac{1}{n(n+1)}\)
Now, we will split the denominator of the nth term into two parts or we will write T_n as the difference of two terms.

Question 5.
Find the sum to n terms of the series 5² + 6² + 7² + … + 20².
Answer.
The given series is 5² + 6² + 7² + … + 20²
nth term, a_n = (n + 4)²
= n² + 8n + 16

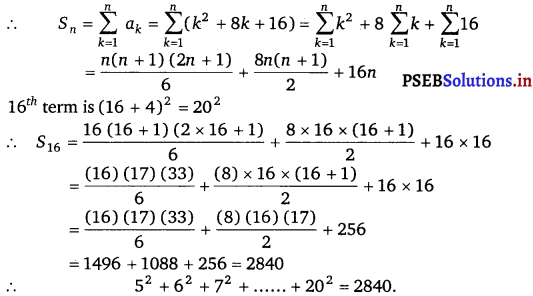
Question 6.
Find the sum to n terms of the series 3 × 8 + 6 × 11 + 9 × 14 + …………..
Answer.
The given series is 3 × 8 + 6 × 11 + 9 × 14 + ………….
a_n = (nth term of 3, 6, 9 ………..) × (nth term of 8, 11, 14, …………)
= (3n) (3n + 5)
= 9n² + 15n

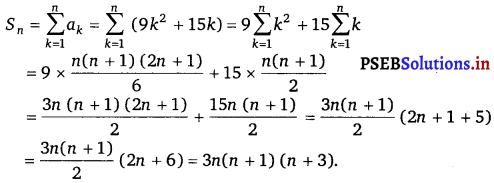
Question 7.
Find the sum to n terms of the series 1² + (1² + 2²) + (1² + 2² + 3²) + ………….
Answer.
Let T_n denote the nth term, then
Tn = 1² + (1² + 2²) + (1² + 2² + 3²) + ………….

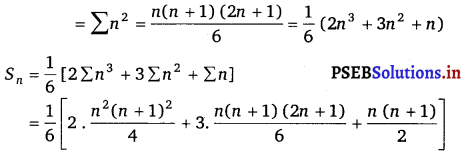
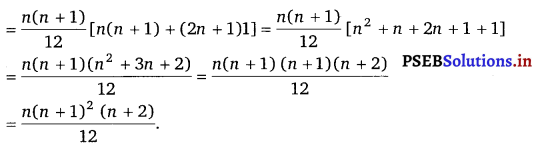
Question 8.
Find the sum to re terms of the series whose nth term is given by n (n + 1) (n + 4).
Answer.
a_n = n (n + 1) (n + 4)
= n(n² + 5n + 4)
= n³ + 5n² + 4n

Question 9.
Find the sum to re terms of the series whose nth term is given by tthe n² + 2n.
Answer.
a_n = n² + 2n
S_n = \(\sum_{k=1}^{n} k^{2}+2^{k}=\sum_{k=1}^{n} k^{2}+\sum_{k=1}^{n} 2^{k}\) …………..(i)
Consider \(\sum_{k=1}^{n} 2^{k}\) = 2¹ + 2² + 2³ + ……………

The above series 2, 2², 2³, … is a G.P. with both the first term and common ratio equal to 2.
\(\sum_{k=1}^{n} 2^{k}=\frac{(2)\left[(2)^{n}-1\right]}{2-1}\) = 2 (2ⁿ – 1) ……………(ii)
Therefore, from eqs. (i) and (ii), we obtain
S_n = \(\sum_{k=1}^{n} 2^{k}\) + 2(2ⁿ – 1)
= \(\frac{n(n+1)(2 n+1)}{6}\) + 2(2ⁿ – 1).

 

Question 10.
Find the sum to re terms of the series whose reth term is given by (2n – 1)².
Answer.
Given, nth term T_n = (2n – 1)²
⇒ T_n = 4 n² + 1 – 4n
Now, S = Σ T_n
= Σ (4n² + 1 – 4n)
= 4 Σn² + Σ 1 – 4 Σn